Simplify these expressions
a) 5x +3x + 2y + 4y
Answers
Answer:
2( 4x + 3y)
Step-by-step explanation:
5x +3x + 2y + 4y
Combine like terms.
8x + 6y
Factorize the answer.
2( 4x + 3y)
Answer: 8x+7y
Step-by-step explanation:
5x+3x+2y+4y
Combine like terms:
Ans: 8x+3y
Related Questions
Find an equation of the lips having a major axis of the length
Answers
Answer:
The amplitude of the function is |-9| = 9 and the period of the function is 2π.
Step-by-step explanation:
he general form of a sinusoidal function is y = A sin(Bx + C) + D, where A is the amplitude, B determines the period, C is the horizontal shift, and D is the vertical shift.
Comparing this form with the given function y = -9 sin(x), we can see that A = -9, C = 0, and D = 0. The coefficient of x is 1, which can be written as B/1. Therefore, we have:
A = -9
B/1 = 1
C = 0
D = 0
Solving for B, we get:
B = 2π/period
Since B/1 = 1, we have B = 1, which implies:
2π/period = 1
Solving for the period, we get:
period = 2π
Therefore, the amplitude of the function is |-9| = 9 and the period of the function is 2π.
To know more about sinusoidal function refer here
https://brainly.com/question/12060967#
#SPJ11
Find the missing value required to create a probability
distribution, then find the standard deviation for the given
probability distribution. Round to the nearest hundredth.
x / P(x)
0 / 0.15
1 / 2
Answers
To create a probability distribution, the missing probability value is 0.65. The standard deviation of the given probability distribution is approximately 0.60.
To find the missing value required to create a probability distribution, we need to determine the probability corresponding to the missing value.
x / P(x)
0 / 0.15
1 / 2
To create a probability distribution, the sum of all probabilities must equal 1. So, we can subtract the given probability from 1 to find the missing probability:
Missing probability = 1 - 0.15 - 0.2 = 0.65
Now, we have the complete probability distribution:
x / P(x)
0 / 0.15
1 / 0.2
2 / 0.65
To find the standard deviation of the given probability distribution, we can use the formula:
Standard deviation = sqrt(Σ((x - μ)^2 * P(x)))
where Σ represents the sum, x is the value, μ is the mean, and P(x) is the probability.
To find the mean (μ), we can calculate it as the weighted average of the values multiplied by their respective probabilities:
μ = (0 * 0.15) + (1 * 0.2) + (2 * 0.65) = 1.35
Now, we can calculate the standard deviation:
Standard deviation = sqrt(((0 - 1.35)^2 * 0.15) + ((1 - 1.35)^2 * 0.2) + ((2 - 1.35)^2 * 0.65))
Standard deviation ≈ sqrt(0.364)
Rounding to the nearest hundredth, the standard deviation is approximately 0.60.
To learn more about standard deviation visit : https://brainly.com/question/475676
#SPJ11
The notation arcsinx represents the inverse sine function.
• A. True
•
B. False
Answers
Answer: False
Step-by-step explanation:
The lower case letter denotes a relation, not a function
I need help with this.
I need to find both A and B, I’m just lost at this point
Answers
What are the x-values where f(x) = 3? The leftmost x-value where f(x) = 3 is when x = 1. What is the rightmost x-value where f(x) = 3?x = _____ ?
Answers
The rightmost x-values when f(x) = 3 in the attached graph of the function is equals to x = 5.
In the attached graph ,
The left most x-value for f(x) = 3 when x = 1
From the graph intersection of f(x) = 3 represents that ( x, y ) coordinates for y = 3 is x = 5.
From the graph value of f( -4 ) is equal to 8
Minimum value of the function is f(3) = -1.
Therefore, the x-values of the function is given by
Rightmost x-value when f(x) = 3 is x = 5.
The value of the function f(-4) = 8.
Minimum value of the function from the attached graph
f(3) = -1.
Learn more about values here
brainly.com/question/29292989
#SPJ4
The above question is incomplete , the complete question is:
Use the graph to find the following:
a. What are the x-values where f(x) = 3? The leftmost x-value where f(x) = 3 is when x = 1. What is the rightmost x-value where f(x) = 3?x = _____ ?
b. What is f(-4) ?
c. What is minimum value of the function?
Graph is attached.

Using the distributive property to solve linear equations 4-2(x+7)=3(x+5)
Answers
Answer:
Solution
=−5 that is the answer im positive
Step-by-step explanation:
4-2x+14=3x+15
-2x-3x=18+15
-5x=33
x=33/-5
please help, thank you if you do help me

Answers
Answer:
Question 1: -3
Question 2: 5
Step-by-step explanation:
Question 1's value decreses by 3 so the answer is -3 :)
Question 2's value increases by 5 so the answer is 5 :)
Have an amazing day!!
Please rate and mark brainliest!!
desperate for help lol

Answers
Hi there! See the Identity below in the box:
\( \large \boxed{(f - g)(x) = f(x) - g(x)}\)
We are also given that:
f(x) = 0g(x) = 7x+9Substitute both values in the equation.
\( \large{(f - g)(x) = 0 - (7x + 9)} \\ \large{(f - g)(x) = - (7x + 9)}\)
Recall the property:
(-)(-) = +(+)(+) = +(-)(+) = -(+)(-) = -Same sign multiplying the same sign = + while opposite = -
Using the distribution property, distribute the negative sign in 7x+9. Since 7x+9 are positive for both terms - distributing in would turn the expression in negative form.
\( \large{(f - g)(x) = - 7x - 9}\)
Hence, the answer is -7x-9.
Questions about the problem and my answer or explanation can be asked through comment.
Furthermore, (f-g)(x) is like a factored form of f(x)-g(x).
Hope this helps, and Happy Learning! :)
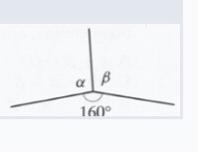
How do I find the variable?

Answers
Answer:
x = 8
Step-by-step explanation:
Step 1:
9x = 72 Def. of an isosceles triangle
Step 2:
x = 72 ÷ 9 Divide
Answer:
x = 8
Hope This Helps :)
i need to find the slope and the value of A B

Answers
Answer:
the slope is 2 and a=8 b=6
Step-by-step explanation:
QuestionQuestion 1Consider the function y=x - 5.What are the domain and range of this function?
Answers
According to the given function, which contains a square root, the domain must contain numbers that are greater than or equal to 5, otherwise, we would obtain the square root of a negative value, which is not real.
It means that the domain is
\(x\ge5\)The range contains numbers greater than 0, this is because the minimum value of the domain is 5, when we evaluate the function at this value, the result is 0, which means that the range is:
\(x\ge0\)The answer is the first option.
a number, y, is equal to twice the sum of a smaller number and 3. the larger number is also equal to 5 more than 3 times the smaller number. which equations represent the situation? 2 x minus y
Answers
The final two equations which represent the given situation are:
2x - y = -6 and 3x - y = -5.
What is the linear equation?
A linear equation is an algebraic equation of the form y=mx+b, where m is the slope and b is the y-intercept, and only a constant and a first-order (linear) term are included. The variables in the preceding equation are y and x, and it is occasionally referred to as a linear equation of two variables.
Suppose,
The larger number is 'y' and the smaller number is 'x'.
First relation,
'y' is equal to twice the sum of a smaller number (x) and 3. So we represent this as:
y = 2(x+3)
y = 2x + 6
2x - y = -6 ............(1)
Second relation,
The larger number (y) is equal to 5 more than 3 times the smaller number (x). So we represent this as:
y = 5 + 3x
3x - y = -5 .............(2)
Hence, the final two equations which represent the given situation are:
2x - y = -6 and 3x - y = -5.
To learn more about the linear equation visit,
https://brainly.com/question/2030026
#SPJ4
How do you find the general solution of an exact differential equation?
Answers
The general solution of an exact differential equation can also be found by solving the associated homogenous equation and adding the particular solution obtained from the original equation.
1. Identify the exact differential equation.
2. Find the integrating factor by multiplying the equation by an expression of the form e^(f(x)).
3. Multiply the integrating factor with the equation to make it exact.
4. Integrate both sides of the equation to obtain the general solution.
5. Check the solution by differentiating it to confirm that it satisfies the original equation.
6. Add the particular solution obtained from the original equation to the homogenous solution to get the general solution.
The general solution of an exact differential equation can be found by using an integrating factor. An integrating factor is a function of the independent variable which can be multiplied with the equation in order to make it exact. Once the equation has been made exact, it can be solved using the standard integration techniques. In addition, the general solution can be found by solving the associated homogenous equation and then adding the particular solution obtained from the original equation.
Learn more about equation here
https://brainly.com/question/29657992
#SPJ4
A company blends two gasolines from High-Quality Fuels and Junk Petroleum (in-
puts) into two commercial products, Super and Regular gasoline (outputs). For
the inputs, the octane ratings, the lead content in grams per litre, and the amounts
available in cubic metres (m3) and their prices are known. These are:
Input Octane Lead Amount Buying Price
Gasoline Rating Content (g/L) Available (m3) ($ per m3)
High-Quality 105 0.10 25,000 350
Junk 82 0.30 30,000 260
For the Super and Regular gasolines the requirements are:
Output Minimum Maximum Minimum Selling
Gasoline Octane Lead Amount Price
Rating Content (g/L) Required (m3) ($ per m3)
Super 95 0.15 10,000 400
Regular 86 0.20 17,000 310
We define the variables as follows: H and J are respectively the amount of gasoline
in m3 purchased from High-Quality Fuels/Junk Petroleum. S and R are respectively
the amount of Super/Regular gasoline in m3 blended and sold. HS, HR, JS, and JR
are respectively the amounts in m3 of High-Quality/Junk gasoline used to make
Super/Regular gasoline.
For this and each of the other four questions which follow, make sure that you
answer parts (a), (b), and (c) as given at the bottom of the previous page.
Answers
To meet the requirements, the company should purchase 6,500 m³ of High-Quality gasoline, 13,500 m³ of Junk gasoline, produce 7,000 m³ of Super gasoline, and 10,000 m³ of Regular gasoline.
To determine the amounts of High-Quality and Junk gasoline to purchase and the amounts of Super and Regular gasoline to produce and sell, we need to consider the octane rating, lead content, and minimum and maximum amounts required for each type of gasoline.
For Super gasoline, the minimum octane rating required is 95, and the minimum lead content required is 0.15 g/L. To meet these requirements, the company needs to blend a certain amount of High-Quality and Junk gasoline. Since the company has 25,000 m³ of High-Quality gasoline available with an octane rating of 105 and 0.10 g/L of lead content, it should purchase 6,500 m³ of High-Quality gasoline to satisfy the minimum octane rating and lead content requirements.
Similarly, since the company has 30,000 m³ of Junk gasoline available with an octane rating of 82 and 0.30 g/L of lead content, it should purchase 13,500 m³ of Junk gasoline to meet the minimum octane rating and lead content requirements.
Now, considering the amounts of Super and Regular gasoline required, the company should produce 7,000 m³ of Super gasoline and 10,000 m³ of Regular gasoline. The Super gasoline should be sold at a price of $400 per m³, and the Regular gasoline should be sold at a price of $310 per m³.
In summary, the company should purchase 6,500 m³ of High-Quality gasoline, 13,500 m³ of Junk gasoline, produce 7,000 m³ of Super gasoline, and sell it at a price of $400 per m³. They should also produce 10,000 m³ of Regular gasoline and sell it at a price of $310 per m³.
Learn more about gasoline
brainly.com/question/13402652
#SPJ11
Find the solution to the system of equations.

Answers
Answer:
(-4,-2)
Step-by-step explanation:
To solve this system of equations, we can substitute the expression for y in the second equation:
5x + 2(x+2) = -24
We can then simplify and solve for x:
5x + 2x + 4 = -24
7x = -28
x = -4
We can then substitute this value of x back into the first equation to find the value of y:
y = -4 + 2
y = -2
So the solution of the system of equations is (x, y) = (-4, -2)
is 3 less than or greater than 3 1/4
Answers
Answer:
less than
Step-by-step explanation:
convert all numbers into improper fractions
3=12/4
3 1/4=13/4
3 1/4 is greater than 3 by 1/4
Answer:
3 is less than 3 1/4
Step-by-step explanation:
3 is after 3 1/4 when you look at a number line
What is the length of AE?

Answers
Answer:
1.5
Step-by-step explanation:
3/2
(1)/(3)-x^(2)+2x+1+x^(2)+4x+4=199 3x^(2)+6x-5-145=0,x+8=0 The square of the sum of two positive, consecutive, even numbers excoseds the sum of their squares by 336 . Find the numbers.
Answers
The two positive, consecutive, even numbers are 12 and 14.
To find the two numbers, we need to use algebra to solve the equation given in the question.
Let x be the first even number and x + 2 be the second even number, since they are consecutive.
According to the question, the square of the sum of these two numbers exceeds the sum of their squares by 336. So we can write the equation as:
\((x + x + 2)^{2} - (x^2 + (x + 2)^2) = 336\)
Simplifying the equation gives:
4x^2 + 8x + 4 - x^2 - x^2 - 4x - 4 = 336
2x^2 + 4x - 336 = 0
Dividing the equation by 2 gives:
x^2 + 2x - 168 = 0
Using the quadratic formula, we can find the value of x:
x = (-2 ± √(2^2 - 4(1)(-168)))/(2(1))
x = (-2 ± √676)/2
x = (-2 ± 26)/2
The two possible values of x are:
x = 12 or x = -14
Since we are looking for positive even numbers, we can disregard the negative value of x.
So the first even number is 12 and the second even number is 12 + 2 = 14.
To know more about consecutive numbers, refer here:
https://brainly.com/question/29775116#
#SPJ11
Dennis, Edwin and Fred had 360 erasers in total. Edwin won some erasers from Dennis. As a result, he had thrice as many erasers as before. Fred then won some erasers from Edwin and Fred's erasers increased by 10%. Finally, Fred lost some of his erasers to Dennis and Dennis's erasers increased by 60%. In the end, they realized they each had an equal number of erasers. How many erasers did Edwin have at first?
Answers
The details of the question indicates relationship equations from which the number of erasers Edwin had at first, is 45 erasers
What is an equation?An equation is a statement of equivalence between expressions.
The number of erasers they each finally had = 360/3 = 120
The number of erasers Dennis had before Fred lost sum erasers to him, x is therefore;
1.60·x = 120
x = 120/1.6 = 75
The number of erasers Fred lost to Dennis = 120 - 75 = 45
Let a, represent the number of erasers Dennis initially had, and let b, represent the number of erasers, Edwin initially had, and let c represent the number of erasers Fred had, we get;
a + b + c = 360
The number of erasers Edwin won from Dennis = 2·b
The number of erasers Dennis then had = a - 2·b
The number of derasers Fred won from Dennis = 0.1·c
The number of erasers Fred then had = 1.1·c
a - 2·b = 75
1.1·c - 45 = 120
c = (120 + 45)/1.1 = 150
a - 2·b = 75...(1)
a + b + 150 = 360
a + b = 360 - 150 = 210
a + b = 210...(2)
a - 2·b = 75
Subtract equation (1) from equation (2), we get;
b - (-2·b) = 210 - 75 = 135
3·b = 135
b = 135/3 = 45
a + 45 + 150 = 360
a = 360 - (45 + 150) = 165
a = 165
The number of erasers Edwin had first, b = 45 erasersLearn more on writing equations here: https://brainly.com/question/24628957
#SPJ1
A family wants to rent a car to go on vacation. Company A charges $40.50 and 8 per mile . Company B charges $70.50 and 12 cents per mile . How much more does charge for x miles than ?
Answers
Company B charges $30 more than Company A for every x miles driven.
Let's begin by calculating the total cost of renting a car from each company:
40.50 + 0.08x, where x is the number of miles driven
B Corporation: 70.50 + 0.12x
We can subtract the expression for Company A from the expression for Company B to find out how much more Company B charges for x miles than Company A:
(70.50 + 0.12x) - (40.50 + 0.08x)
When we simplify, we get:
30 + 0.04x
As a result, Company B charges $30 more per x miles driven than Company A.
To know more about Miles visit:
https://brainly.com/question/12665145
#SPJ1
Prominent candy company Sweetums and fast food chain Paunch Burger decide to team up and release a new child-sized drink that blends candy bars into milkshakes. Leslie Knope is interested in how this new milkshake affects the weight of the citizens of her town (Pawnee, Indiana). She decides to take a random sample of 41 people from the town and asks the people in the sample to replace one beverage a day with this new candy bar milkshake. She measures their weights (in kilograms) before and after drinking this milkshake for a week. The summary of the data is below.
Variable Sample Mean Sample Standard Deviation
Weight (After - Before) 3.51 7.44
Use a significance level of α = 0.01 to test the hypothesis that the mean weight of citizens in Pawnee significantly increased after drinking the new child-sized candy bar milkshake from Sweetums and Paunch Burger for a week. Assume that the necessary conditions hold to carry out this test.
Select one:
t = 2.293, p-value < 0.01, reject the null hypothesis, and conclude that the mean weight of the citizens has increased.
t = 2.293, p-value < 0.01, reject the null hypothesis, and conclude that the mean weight of the citizens has changed.
t = 3.021, p-value > 0.01, do not reject the null hypothesis, conclude that the mean weight of the citizens has stayed the same.
t = 2.293, p-value > 0.01, do not reject the null hypothesis, conclude that the mean weight of the citizens has stayed the same.
t = 3.021, p-value < 0.01, reject the null hypothesis, and conclude that the mean weight of the citizens has increased.
To estimate the effect of the new child-sized candy bar milkshake, Leslie finds a 95% confidence interval for the mean difference in weight to be (1.163 , 5.857).
Answers
The correct answer is: t = 2.293, p-value < 0.01, reject the null hypothesis, and conclude that the mean weight of the citizens has increased.
To test the hypothesis, we need to use a one-sample t-test since we are comparing the mean weight difference of the sample to zero (no change). The sample mean weight difference is 3.51, and the sample standard deviation is 7.44. Since we do not know the population standard deviation, we use the t-distribution.
The null hypothesis is that the mean weight difference is equal to zero (no change), and the alternative hypothesis is that the mean weight difference is greater than zero (increase in weight).
Using a significance level of 0.01, the critical t-value for a one-tailed test with 40 degrees of freedom is 2.704. The calculated t-value is (3.51-0)/(7.44/sqrt(41)) = 2.293. The p-value associated with this t-value is less than 0.01 (found using a t-distribution table or calculator).
Since the p-value is less than the significance level, we reject the null hypothesis and conclude that the mean weight of the citizens of Pawnee significantly increased after drinking the new candy bar milkshake for a week. Therefore, the correct answer is: t = 2.293, p-value < 0.01, reject the null hypothesis, and conclude that the mean weight of the citizens has increased.
The 95% confidence interval for the mean difference in weight (1.163 , 5.857) also supports this conclusion since it does not include zero.
To learn more about significance level, refer below:
https://brainly.com/question/13947717
#SPJ11
Solve the triangle. Round your answers to the nearest tenth.

Answers
Answer:
<B = 47°
<C = 28°
b = AC = 28.0
Step-by-step explanation:
Given:
∆ABC
AB = c = 18
BC = a = 37
<A = 105°
Required:
Length of AC = b
measure of angle B and angle C
SOLUTION:
==>Use the sine rule, sin A/a = sinC/c to find the angle of C:
SinA = sin(105) = 0.9659
a = 37
sinC = ?
c = 18
0.9659/37 = sinC/18
Cross multiply
0.9659*18 = 37*sinC
17.3862 = 37*sinC
Divide both sides by 37
17.3862/37 = sinC
0.4699 = sinC
sinC = 0.4699
C = Sin-¹(0.4699)
C = 28.0° (nearest tenth)
==>Find angle B using sum of angles in a triangle:
Angle B = 180 - (105+28)
Angle B = 180 - 133
Angle B = 47°
==>Find length of b using sine rule, b/sinB = c/sinC:
SinC = sin(28) = 0.4695
SinB = sin(47) = 0.7314
c = 18
b = ?
b/0.7314 = 18/0.4695
Cross multiply
b*0.4695 = 18*0.7314
b*0.4695 = 13.1652
Divide both sides by 0.4695
b = 13.1652/0.4695
b = 28.0 (nearest tenth)
Scientists have hypothesized that npy is necessary for the generation of the preovulatory lh surge, a hormonal event that triggers ovulation. Which findings best supports this hypothesis?
Answers
The best findings that support the hypothesis that NPY is necessary for the generation of the preovulatory LH surge include studies that show NPY acting on neurons in the hypothalamus, which is a critical brain region involved in regulating reproductive functions.
Additionally, experiments in animals have shown that disrupting NPY signaling can prevent the preovulatory LH surge and ovulation. Finally, clinical studies in women have found that alterations in NPY levels or activity can lead to menstrual irregularities and infertility, further supporting the role of NPY in ovulation.
To best support the hypothesis that NPY (neuropeptide Y) is necessary for the generation of the preovulatory LH (luteinizing hormone) surge, which triggers ovulation, scientists would need to find evidence such as:
1. A positive correlation between NPY levels and LH surge timing, indicating that higher NPY levels are associated with the initiation of the LH surge.
2. Experimental manipulation of NPY levels leading to changes in LH surge and ovulation, showing a cause-and-effect relationship between NPY and the hormonal event.
3. Identification of NPY receptors on the gonadotropin-releasing hormone (GnRH) neurons, which are responsible for releasing LH, suggesting a direct mechanism of action.
These findings would provide strong evidence for the proposed role of NPY in the generation of the preovulatory LH surge and ovulation.
To learn more about hypothesis visit;
https://brainly.com/question/29519577
#SPJ11
find the value of the slope and the type of slope

Answers
Answer:
-5
Step-by-step explanation:
Each time the x value goes up 1, the y value goes down 5.
change in x = 1
change in y = -5
slope = (change in y)/(change in x)
slope = -5
Answer:
-five
Step-by-step explanation:
rise over run
8. Complete the table below by drawing an example of each shape.

Answers
Answer:
Please see attachment.
The first one is a quadrilateral that is not a parallelogram.
The second one is a triangle with a right angle.
Step-by-step explanation:
Hope this helps!
If not, I am sorry.


Given: 2x^2+X-3 and g(X)=x-1
Express f(X)•g(X)-[f(X)+g(X)]
Answers
Answer:
[40]. Question 33. 33 Given: f(x) 2x2 x. 3 and g(x) x. 1. Express f(x) • g(x) [f(x) g(x)] as a polynomial in standard form. Score 4: The student gave a ...
Step-by-step explanation:
Solve f(x)=2x^2+x-3 , g(x)=x-1 ; (f(x))/(g(x)). f(x)=2x2+x−3 f ( x ) = 2 x 2 + x - 3 , g(x)=x−1 g ( x ) = x - 1 ; f(x)g(x) f ( x ) g ( x ). Remove parentheses. 2x2+x−3 2 x 2 ...9(-3):21-3)+1. =-6+T. + 9(-3) = -5 f(-5)=31-5)-5. = -15-5-20. 5. f(x) = 5x – 6 g(x) = 3x. Find f(g(x)) f(3x). 5(3x)-6. (15x-6). 3. f(x)= 3x - 5 g(x) = 2x + 1 4. f(x)= x – 2 ...
Let X and Y denote the tarsus lengths of male and female grackles, respectively. Assume that X is N(,) and Yis N(4,²). Given that the sample number of X and Y are n=m=25, and X = 33.8, S=3.9,Y=32.5, S=5.1. Use these observations to give a level a=0.05 test for H₁:μx = μy VS Hoxy. Give the p-value of this test. (10 pts)
Answers
To test the hypothesis H₁: μx = μy versus Hoxy, where μx and μy represent the means of X and Y respectively, we can perform a two-sample t-test. The test compares the means of two independent samples to determine if they are significantly different from each other.
The given information provides the sample means (X = 33.8, Y = 32.5) and the sample standard deviations (Sx = 3.9, Sy = 5.1). The sample sizes for both X and Y are n = m = 25.
Using this information, we can calculate the test statistic, which is given by:
t = (X - Y) / sqrt((Sx^2 / n) + (Sy^2 / m))
Plugging in the values, we get:
t = (33.8 - 32.5) / sqrt((3.9^2 / 25) + (5.1^2 / 25))
Next, we need to determine the degrees of freedom for the t-distribution. Since the sample sizes are equal (n = m = 25), the degrees of freedom for the test is given by (n + m - 2).
Using the t-distribution table or software, we can find the critical value corresponding to a significance level of α = 0.05 and the degrees of freedom.
Finally, we compare the calculated test statistic with the critical value. If the test statistic falls within the rejection region (i.e., the absolute value of the test statistic is greater than the critical value), we reject the null hypothesis. The p-value can also be calculated, which represents the probability of observing a test statistic as extreme or more extreme than the calculated value, assuming the null hypothesis is true.
Learn more about probability here: brainly.com/question/13604758
#SPJ11
Mía ha comprado un terreno en el emporio de Gamarra.
Si desea destinar la mayor superficie rectangular posible del terreno para colocar su maquinaria, ¿cuánto mide la superficie del terreno que queda disponible para otros ambientes?
Un reto para obtener el Logro destacado:
Mía desea comprar un segundo terreno, esta vez de forma rectangular, cuya área sea de 650 m2 y para ello evalúa las posibles dimensiones que puede tener dicho terreno. Si quiere gastar lo menos posible en cercar el terreno, ¿cuáles deben ser sus dimensiones? (Considera como medida de las dimensiones solo números enteros) (Cercar es rodear un terreno, con una cerca, valla, muro, etc., para delimitarlo.)

Answers
Answer:
mkana
Step-by-step explanation:
evaluate (x)=7x3+6x4-8x6+6x+11 atx=0.
Answers
Answer:
11
Step-by-step explanation:
teacher just explained it to me and i forgot it and i only remembered the answer
determine whether the series is convergent or divergent. [infinity] k = 1 ke−k2
Answers
Answer:
Convergent
Step-by-step explanation:
One method to determine if \(\displaystyle \sum^\infty_{k=1}ke^{-k^2}\)is convergent or divergent is the Integral Test.
Suppose that the function we use is \(f(x)=xe^{-x^2}\). Over the interval \([1,\infty)\), the function is always positive and continuous, but we also need to make sure it is decreasing before we can proceed with the Integral Test.
The derivative of this function is \(f'(x) = e^{-x^2}(1-2x^2)\), so our critical points will be \(\displaystyle x=\pm\frac{1}{\sqrt{2}}\), but we can drop the negative critical point as we are starting at \(k=1\). Using some test points, we can see that the function increases on the interval \(\bigr[0,\frac{1}{\sqrt{2}}\bigr]\) and decreases on the interval \(\bigr[\frac{1}{\sqrt{2}},\infty\bigr)\). Since the function will eventually decrease, we can go ahead with the Integral Test:
\(\displaystyle \int_{{\,1}}^{{\,\infty }}{{x{{{e}}^{ - {x^2}}}\,dx}} & = \mathop {\lim }\limits_{t \to \infty } \int_{{\,1}}^{{\,t}}{{x{{{e}}^{ - {x^2}}}\,dx}}\hspace{0.5in}u = - {x^2}\\ & = \mathop {\lim }\limits_{t \to \infty } \left. {\left( { - \frac{1}{2}{{{e}}^{ - {x^2}}}} \right)} \right|_1^t\\ & = \mathop {\lim }\limits_{t \to \infty } \left( {-\frac{1}{2}{{e}}^{ - {t^2}}-\biggr(-\frac{1}{2e}\biggr)}} \right) = \frac{1}{2e}\)
Therefore, since the integral is convergent, the series must also be convergent by the Integral Test.