Simplify negative 8 over 3 divided by negative 2 over 6.
Answers
Answer:
8/9
Step-by-step explanation:
Answer:
The answer is 8
Step-by-step explanation:
Was i right?
Related Questions
Determine if the function is a polynomial function. If the function is a polynomial function, state the degree and leading coefficient. If the function is not a polynomial, state why. f(x)=x^4(2-x^3)+1

Answers
Answer:
The correct option is
This is a polynomial function of degree 7 with a leading coefficient of -1
Step-by-step explanation:
Functions that consist of a variable such as x raised to positive integer powers which are equal to or larger than zero added together to make the function are known as polynomial functions
Therefore, the function in the question which is f(X) = x⁴ × (2 - x³) + 1
Which can be expanded as follows
f(x) = 2·x⁴ - x⁷ + 1, which is the same as given as follow equation;
f(x) = -x⁷ + 2·x⁴ + 1
Which is polynomial function with a leading coefficient of -1 as it consists of only whole number positive powers of x including the powers of x 4 and 7
Therefore, the correct option is that f(x) is a polynomial function of degree 7 with a leading coefficient of -1.
What is the answer to 6(x-3) — 2(x - 5)?
Answers
Answer:
4x-8
Step-by-step explanation:
(6(x) - 6(3)) - (2(x) - 2(5))
6x - 18 - 2x + 10
Now combine like terms.
6x - 2x
-18 + 10
3x - 8
Since we cannot do any operations between a number with a variable and a number without. 3x - 8 is our final answer.
a survey of 20 colleges found that seniors graduated with an average of $12,000 in debt from student loans. the debt was normally distributed with a standard deviation of $3200. find the probability that a senior graduated owing more than $16000.
Answers
The probability that a senior graduated owing more than $16,000 in student loan debt is approximately 0.1056 or 10.56%.
What is the likelihood of a senior graduating with over $16,000 in student loan debt?To find the probability that a senior graduated owing more than $16,000 in student loan debt, we can use the standard normal distribution and z-scores.
Let's denote X as the student loan debt of a senior. Given that the debt is normally distributed with a mean (μ) of $12,000 and a standard deviation (σ) of $3,200, we want to calculate P(X > $16,000).
First, we need to calculate the z-score, which measures the number of standard deviations that $16,000 is away from the mean:
z = (X - μ) / σ
Plugging in the values:
z = ($16,000 - $12,000) / $3,200
z ≈ 1.25
Next, we find the area under the standard normal curve to the right of the z-score of 1.25. This represents the probability of a senior having a debt of $16,000 or less.
P(X ≤ $16,000) = 0.8944
To find P(X > $16,000), we subtract this probability from 1:
P(X > $16,000) = 1 - P(X ≤ $16,000)
P(X > $16,000) ≈ 1 - 0.8944
P(X > $16,000) ≈ 0.1056
Therefore, the probability that a senior graduated owing more than $16,000 in student loan debt is approximately 0.1056 or 10.56%.
Learn more about Probability
brainly.com/question/31120123
#SPJ11
Solve the equation 2x - 56 = 8
Answers
Solution,
2x-56=8
or,2x=8+56
or,2x=64
or,X=64/2
X=32
Hope it helps
Good luck on your assignment
Answer:
x=32
Step-by-step explanation:
First I put the 56 on the other side by doing the opposite to it, so adding 56 to both sides.
2x - 56 = 8
+56 +56
2x=64
Then divide both sides by two to single out the x and know it's value
2x=64
/2 /2
x=32
what is a polygon with all sides and angles congruent
Answers
A regular polygon is a polygon with all sides and angles congruent. It exhibits symmetry and uniformity in its sides and angles, creating a visually appealing shape.
A polygon with all sides and angles congruent is called a regular polygon. In a regular polygon, all sides have the same length, and all angles have the same measure. This uniformity in the lengths and angles of the polygon's sides and angles gives it a symmetrical and balanced appearance.
Regular polygons are named based on the number of sides they have. Some common examples include the equilateral triangle (3 sides), square (4 sides), pentagon (5 sides), hexagon (6 sides), and so on. The names of regular polygons are derived from Greek or Latin numerical prefixes.
In a regular polygon, each interior angle has the same measure, which can be calculated using the formula:
Interior angle measure = (n-2) * 180 / n
Where n represents the number of sides of the polygon.
The sum of the interior angles of any polygon is given by the formula:
Sum of interior angles = (n-2) * 180 degrees
Regular polygons have several interesting properties. For instance, the
exterior angles of a regular polygon sum up to 360 degrees, and the measure of each exterior angle can be calculated by dividing 360 degrees by the number of sides.
Regular polygons often possess symmetrical properties and are aesthetically pleasing. They are commonly used in design, architecture, and various mathematical applications.
Learn more about polygon here:
https://brainly.com/question/17756657
#SPJ11
Describe the relationship between the area of a circle and its circumference.
The is times the times the circumference.
Answers
Answer:
The area is twice the circumference
Area = 2 * circumference
Step-by-step explanation:
Proof:
r = 2
Circumference = 2\(\pi\)r
Circumference = 12.566
Area = \(\pi\)r^2
Area = 25.132
25.132/12.566 ≈ 2
Answer:
the (area) is (1/2) times the (radius) times the circumference.
Step-by-step explanation:
i dont know how to explain it exactly but i found the cerect answer.
a trade of securities between a bank and an insurance company without using the services of a broker-dealer would take place on the fourth market first market second market third market
Answers
A trade of securities between a bank and an insurance company without using the services of a broker-dealer would take place on the over-the-counter (OTC) market, also known as the fourth market.
The first market refers to the primary market, where newly issued securities are bought and sold directly between the issuer and investors. This market is typically used for initial public offerings (IPOs) and the issuance of new securities.
The second market refers to the organized exchange market, such as the New York Stock Exchange (NYSE) or NASDAQ, where securities are traded on a centralized platform. This market involves the buying and selling of already issued securities among investors.
The third market refers to the trading of exchange-listed securities on the over-the-counter market, where securities that are listed on an exchange can also be traded off-exchange. This market allows for direct trading between institutions, such as banks and insurance companies, without the involvement of a broker-dealer.
Therefore, in the scenario described, the trade of securities between the bank and insurance company would take place on the fourth market, which is the over-the-counter market.
Learn more about over-the-counter market
https://brainly.com/question/32096837
#SPJ11
3. Jessie is looking for the volume of the cone
below, and she is using the formula V = (1/3)Bh.
Which of the following is the value of “B”?

Answers
Answer:
A
Step-by-step explanation:
The base is the circle.
To find the area of the circle, use pi*r^2
pi = 3.14
r = 6
Area = 3.14 * 6^2Area = 3.14 * 36Area = 113.04Answer:
C. 414.48
Step-by-step explanation:
1/3 x 3.14 x 6² x 11 = 4.14.48
What is the value of the expression
−2 + (−8.5) − (−9 14)?
Express the answer as a decimal.
Answers
The value of the expression −2 + (−8.5) − (−9 * 14) is 115.5.
To find the value of the expression, let's simplify it step by step:
−2 + (−8.5) − (−9 * 14)
Multiplying −9 by 14:
−2 + (−8.5) − (−126)
Now, let's simplify the negations:
−2 + (−8.5) + 126
Next, we can combine the numbers:
−10.5 + 126
Adding −10.5 to 126:
115.5
Therefore, the value of the expression −2 + (−8.5) − (−9 * 14) is 115.5.
For more such questions on expression , Visit:
https://brainly.com/question/1859113
#SPJ11
Jodie wanted to match Mandy's obstacle course record of 68.2 seconds. She had already spent forty and one fourth seconds on wall climbing and 12.84 seconds on the ropes. How much time did she have left to match the record?
12.20 seconds
15.11 seconds
53.09 seconds
55.36 seconds
Answers
What is angle y and z
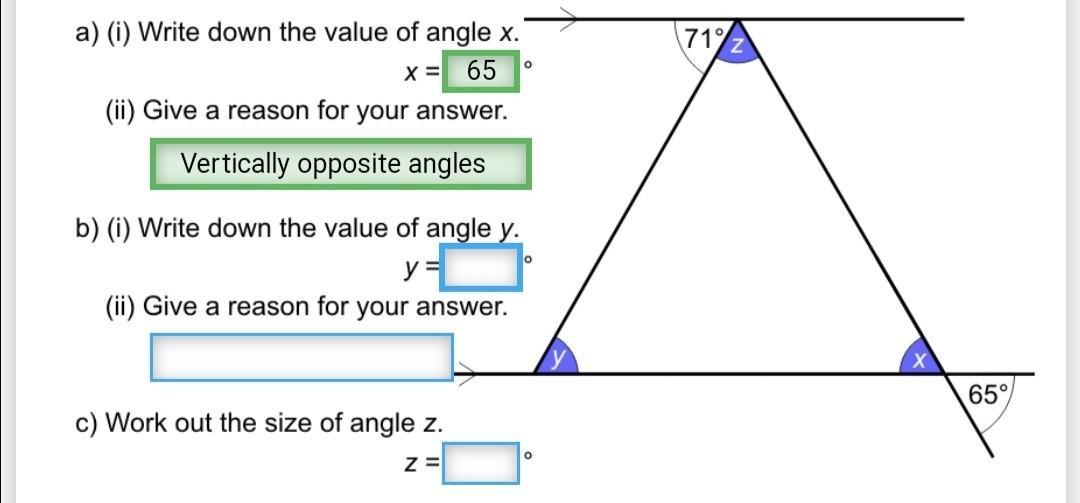
Answers
Answer:
Step-by-step explanation:
y = 71
Reason: Alternate angles
Z = 180-65-71
Z = 44
Solve each equation for θ with 0 ≤ θ <2 π.
2 sin² θ-1=0
Answers
The solutions of the given equation for 0 ≤ θ < 2π are θ1 = 0.7854 and θ2 = 2.3562, are found using the trigonometric identity.
The equation 2sin²θ − 1 = 0 needs to be solved for θ.
Using the trigonometric identity
sin²θ + cos²θ = 1,
we can obtain an equivalent form of the given equation.
2sin²θ − 1 = 0
⟺ 2sin²θ = 1
⟺ sin²θ = 1/2
Taking the square root of both sides, we obtain:
sinθ = ±(1/√2)
We know that
sinθ = y/r
and
cosθ = x/r for an angle θ in standard position.
Thus, y/r can be written as 1/√2 or −1/√2.
We are told that 0 ≤ θ < 2π, which means that we need to find the values of θ in the first and second quadrants that satisfy the above equation.
θ1 = sin⁻¹(1/√2) and
θ2 = π − sin⁻¹(1/√2).
Using a calculator, we get:
θ1 = 0.7854 radians (45°)
and
θ2 = 2.3562 radians (135°)
Know more about the trigonometric identity
https://brainly.com/question/7331447
#SPJ11
1) Given a triangle ABC, such that: BC = 6 cm; ABC = 40° and ACB = 60°. 1) Draw the triangle ABC. 2) Calculate the measure of the angle BAC. 3) The bisector of the angle BAC intersects [BC] in a point D. Show that ABD is an isosceles triangle. 4) Let M be the midpoint of the segment [AB]. Show that (MD) is the perpendicular bisector of the segment [AB]. 5) Let N be the orthogonal projection of D on (AC). Show that DM = DN.
Answers
Step-by-step explanation:
1) To draw triangle ABC, we start by drawing a line segment BC of length 6 cm. Then we draw an angle of 40° at point B, and an angle of 60° at point C. We label the intersection of the two lines as point A. This gives us triangle ABC.
```
C
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/_60° 40°\_
B A
```
2) To find the measure of angle BAC, we can use the fact that the angles in a triangle add up to 180°. Therefore, angle BAC = 180° - 40° - 60° = 80°.
3) To show that ABD is an isosceles triangle, we need to show that AB = AD. Let E be the point where the bisector of angle BAC intersects AB. Then, by the angle bisector theorem, we have:
AB/BE = AC/CE
Substituting the given values, we get:
AB/BE = AC/CE
AB/BE = 6/sin(40°)
AB = 6*sin(80°)/sin(40°)
Similarly, we can use the angle bisector theorem on triangle ACD to get:
AD/BD = AC/BC
AD/BD = 6/sin(60°)
AD = 6*sin(80°)/sin(60°)
Since AB and AD are both equal to 6*sin(80°)/sin(40°), we have shown that ABD is an isosceles triangle.
4) To show that MD is the perpendicular bisector of AB, we need to show that MD is perpendicular to AB and that MD bisects AB.
First, we can show that MD is perpendicular to AB by showing that triangle AMD is a right triangle with DM as its hypotenuse. Since M is the midpoint of AB, we have AM = MB. Also, since ABD is an isosceles triangle, we have AB = AD. Therefore, triangle AMD is isosceles, with AM = AD. Using the fact that the angles in a triangle add up to 180°, we get:
angle AMD = 180° - angle MAD - angle ADM
angle AMD = 180° - angle BAD/2 - angle ABD/2
angle AMD = 180° - 40°/2 - 80°/2
angle AMD = 90°
Therefore, we have shown that MD is perpendicular to AB.
Next, we can show that MD bisects AB by showing that AM = MB = MD. We have already shown that AM = MB. To show that AM = MD, we can use the fact that triangle AMD is isosceles to get:
AM = AD = 6*sin(80°)/sin(60°)
Therefore, we have shown that MD is the perpendicular bisector of AB.
5) Finally, to show that DM = DN, we can use the fact that triangle DNM is a right triangle with DM as its hypotenuse. Since DN is the orthogonal projection of D on AC, we have:
DN = DC*sin(60°) = 3
Using the fact that AD = 6*sin(80°)/sin(60°), we can find the length of AN:
AN = AD*sin(20°) = 6*sin(80°)/(2*sin(60°)*cos(20°)) = 3*sin(80°)/cos(20°)
Using the Pythagorean theorem on triangle AND, we get:
DM^2 = DN^2 + AN^2
DM^2 = 3^2 + (3*sin(80°)/cos(20°))^2
Simplifying, we get:
DM^2 = 9 + 9*(tan(80°))^2
DM^2 = 9 + 9*(cot(10°))^2
DM^2 = 9 + 9*(tan(80°))^2
DM^2 = 9 + 9*(cot(10°))^2
DM^2 = 9 + 9*(1/tan(10°))^2
DM^2= 9 + 9*(1/0.1763)^2
DM^2 = 9 + 228.32
DM^2 = 237.32
DM ≈ 15.4
Similarly, using the Pythagorean theorem on triangle ANC, we get:
DN^2 = AN^2 - AC^2
DN^2 = (3*sin(80°)/cos(20°))^2 - 6^2
DN^2 = 9*(sin(80°)/cos(20°))^2 - 36
DN^2 = 9*(cos(10°)/cos(20°))^2 - 36
Simplifying, we get:
DN^2 = 9*(1/sin(20°))^2 - 36
DN^2 = 9*(csc(20°))^2 - 36
DN^2 = 9*(1.0642)^2 - 36
DN^2 = 3.601
Therefore, we have:
DM^2 - DN^2 = 237.32 - 3.601 = 233.719
Since DM^2 - DN^2 = DM^2 - DM^2 = 0, we have shown that DM = DN.
Enter the equation of the line in slope-intercept form.
The line parallel to y =
5
4
x + 8 that passes through (−8, 0).
The equation of the line that passes through (−8, 0) is y = ???
Answers
Answer:
typing this answer to get points hope u get ur answer soon :)
Step-by-step explanation:
Suppose that you deposit 500 dollars each month into a savings account that earns 1.7 percent interest per year, compounded monthly. In 8 years (immediately after making the 96th deposit), how much money will be in the bank? Round your answer to the nearest penny. Number dollars.
Answers
To calculate the total amount of money in the bank after 8 years, we can use the formula for compound interest: A = P(1 + r/n)^(nt), we find that the final amount in the bank after 8 years is approximately $47,223.57.
In this case, the principal amount is $500, the interest rate is 1.7 percent (or 0.017 in decimal form), the interest is compounded monthly (n = 12), and the time period is 8 years (t = 8). Plugging these values into the formula, we get:
A = 500(1 + 0.017/12)^(12*8)
Evaluating this expression, we find that the final amount in the bank after 8 years is approximately $47,223.57. Rounding this to the nearest penny, the answer is $47,223.57.
To learn more about compound interest click here : brainly.com/question/14295570
#SPJ11
Which explains, on a given day, which island is more likely to have a wind speed close to its median? Country A because the median is closer to one end of the box in the box plot. Country B because the median is closer to the center of the box in the box plot. Country A because it has a smaller interquartile range. Country B because it has a larger interquartile range
Answers
As per the given box plot, on 6th day island is more likely to have a wind speed close to its median.
The term box plot in math referred as the method of visually show the distribution of numerical data and skewness through displaying the data quartiles and averages.
Here we have given the figure attached that contains the box plots show the average wind speeds, in miles per hour, for two different islands Here the Country A is placed on the top of the line where as Country B on the bottom of the line.
While we looking into the box plot we have identified that the median of Country A is 4 and the center of the box is 5
And the the median of Country B is 6 and the center of the box is 6.5.
Through this we have identified that the resulting day is 6 day.
To know more about Box plot here
https://brainly.com/question/1523909
#SPJ4
your quidditch league has 5 teams. you will play a tournament next week in which every team will play every other team once. each team can play at most one match each day, but there is plenty of time in the day for multiple matches. what is the fewest number of days over which the tournament can take place?
Answers
The fewest number of days over which the tournament can take place is 5 days.
How to calculate the number of days?As each team plays with other team Once and we have total 5 teams so number of matches will be (4+3+2+1)
Counted as team 1 plays with all other teams = 4 matches
Team 2 plays with team 3,4,5 =3 matches
Team 3 play with team 4,5=2 match
And the last match is between team 4 and team5
Total match = 10 and can be played two matches per day:
Number of days = 10/2
= 5 days.
Learn more about expressions on:
https://brainly.com/question/723406
#SPJ1
The approximate weights of two animals are 5.36 x 104 lbs. and 6.2 x 104 lbs. Find the total weight of the two animals. Write the final answer in scientific notation with the correct number of significant digits.
Answers
Answer:
12*10^4 lbs.
Step-by-step explanation:
This is the correct answer because you have to count using scientific notation by seeing the amount of times the decimal point has moved to the left which makes it positive.
The total weight of the two animals is 12x10⁴ lbs if the approximate weights of the two animals are 5.36 x 10⁴ lbs. and 6.2 x 10⁴ lbs.
What is an arithmetic operation?It is defined as the operation in which we do the addition of numbers, subtraction, multiplication, and division. It has basic four operators that is +, -, ×, and ÷.
It is given that:
The approximate weights of the two animals are 5.36 x 10⁴ lbs. and 6.2 x 10⁴ lbs.
The total weight = 5.36 x 10⁴ + 6.2 x 10⁴
The total weight = (5.36+ 6.2)10⁴
The total weight = 11.56x10⁴
Or
The total weight = 12x10⁴ lbs
Thus, the total weight of the two animals is 12x10⁴ lbs if the approximate weights of the two animals are 5.36 x 10⁴ lbs. and 6.2 x 10⁴ lbs.
Learn more about the arithmetic operation here:
brainly.com/question/20595275
#SPJ5
In a group of twelve people, four had been selected for a transfer. If two of the twelve are selected, what is the probability that both of those selected are selected for a transfer?
about 5%
about 9%
about 12%
about 15%
Answers
Answer:
9%
Step-by-step explanation:
Probability of the first person being selected is 4/12 and the probability of the second person being selected is 3/11
The probability of both is:
4/12 x 3/11
= 1/11 which is 9%
\(\displaystyle\\|\Omega|=\binom{12}{2}=\dfrac{12!}{2!10!}=\dfrac{11\cdot12}{2}=66\\|A|=\binom{4}{2}=\dfrac{4!}{2!2!}=\dfrac{3\cdot4}{2}=6\\\\P(A)=\dfrac{6}{66}=\dfrac{1}{11}\approx9\%\)
what are the two basic tools for doing geometric constructions
Answers
Answer:
Compass, and straightedge/ruler.
Step-by-step explanation:
The two basic tools for doing geometric constructions are:
Compass: A compass is a drawing tool that consists of two arms, one with a sharp point and the other with a pencil or pen. It is used to draw circles, arcs, and to mark off distances.
Straightedge or Ruler: A straightedge is a tool with a straight, unmarked edge. It is used to draw straight lines, measure lengths, and create parallel or perpendicular lines.
These two tools, the compass and straightedge (or ruler), are fundamental for performing geometric constructions, where precise shapes and figures are created using only these tools and basic geometric principles.
Happy Juneteenth!
given: f(x)=-1/7√16-x^2, find f^-1(x). then state whether f^-1(x) is a function

Answers
The inverse of the function \(f(x) = \frac{1}{7}\sqrt{16 - x^2}\) is, \(f^{-1} (x) = \frac{1}{7}\sqrt{16 +x^2\).
What is an inverse function?First to be an inverse function that function needs to one to one function, meaning every different preimage must correspond to a different image.
We can obtain the inverse of a function by switching the variables x and y with their respective positions and solving for y in terms of x.
Given, A function, \(f(x) = \frac{1}{7}\sqrt{16 - x^2}.\)
let, \(y = \frac{1}{7}\sqrt{16 - x^2}.\)
\(y^2 = (\frac{1}{7})^2(\sqrt{16 - x^2})^2.\)
\(y^2 = (\frac{1}{49})({16 - x^2}).\)
\(y^2 = (\frac{16}{49} - \frac{x^2}{49}).\)
\(\frac{x^2}{49} = \frac{16}{49} + y^2.\)
\(x^2 = 16 + \frac{y^2}{49}.\)
\(x = \sqrt{16 + \frac{y^2}{49}}.\)
\(f^{-1} (x) = \frac{1}{7}\sqrt{16 +x^2\).
learn more about inverse functions here :
https://brainly.com/question/2541698
#SPJ1
Find the value of W if the
perimeter is 54cm
W
W
W
W
W
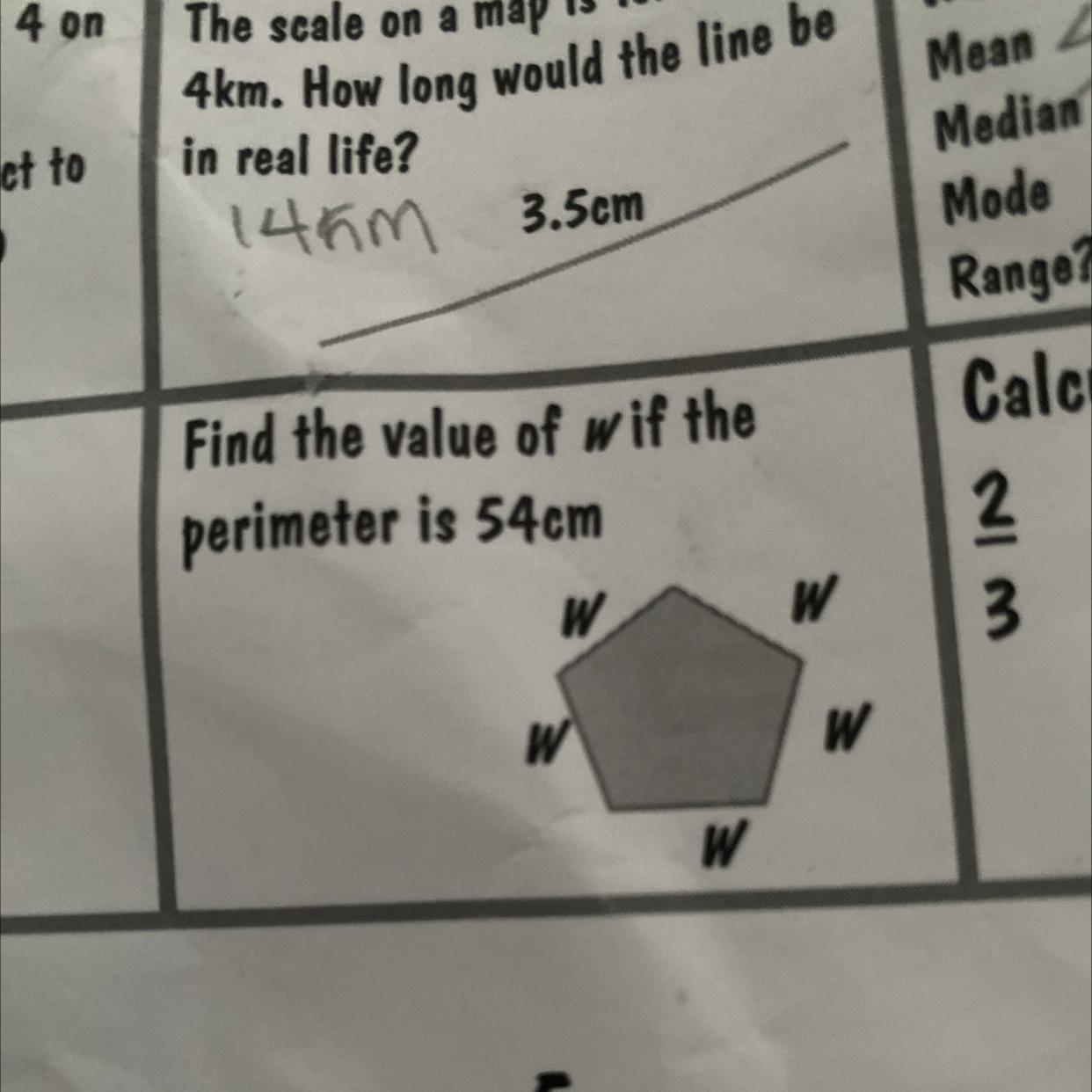
Answers
Answer:
10.8cm
Step-by-step explanation:
54/n= ???
Where n is the number of sides
So N=5 meaning
54/5= 10.8
Therefore, 10.8cm is W
Stevie can refinish a driveway in 4 hours. Ray can refinish the same driveway in 3 hours. Princess can refinish the same driveway in 2 hours. If all three work together, how long would it take them to refinish 5 driveways? Show all work
Answers
Answer: 45 because 4+3+2=9 and 9x5=45
What is the probability of getting a number greater than or equal to 5 when rolling a number cube numbered 1 to 6?
Answers
Answer:
There is a 1/3 (or 0.33%) probability of rolling a number greater than or equal to 5.
Step-by-step explanation:
First, find what numbers are greater than or equal to 5:
5 and 6
Find what options you can get on a number cube:
1, 2, 3, 4, 5, and 6
Out of the 6 possible outcomes, there are only 2 that will get a number greater than or equal to 5. Write this as a fraction:
2/6
Simplify:
1/3
Can you explain how to do this?

Answers
Answer:
a) missing y-values: 4, 8
b) correct: y-intercept = 1
c) y = 2^x
Step-by-step explanation:
a)You complete the table by reading point values from the graph. You have already correctly filled the y-values for x=0 and x=1. The y-value at x=2 is 4. The y-value at x=3 is off the chart, but we expect it to follow the same pattern: it will be 2×4 = 8.
The table values are (x, y) = (0, 1), (1, 2), (2, 4), (3, 8).
__
b)The y-intercept is the point where the graph crosses the y-axis: (0, 1). You have correctly identified 1 as the y-intercept.
__
c)The equation for the curve will be an exponential of the form ...
y = a·b^x
The value of 'a' is the y-intercept: 1.
The value of 'b' is the ratio of successive y-values when x increases by 1.
b = 2/1 . . . for x=1 and x=0
The equation will be ...
y = 1·2^x
y = 2^x . . . . . simplified
Mr thompson!! Please help me sir!




Answers
Answers:
11) D. $3012) Two answers: choice C, choice D13) A. Subtract 100 from each side14) A. n = 9 and n = -5====================================================
Explanation:
11) We set p(120-4p) equal to zero to find that p = 0 is one solution and 120-4p = 0 leads to p = 30. The prices of $0 and $30 both lead to $0 in revenue. It sounds like your teacher wants the larger price value.12) We set each of the two revenue expressions equal to 600.13) Replace the (n-2)^2 with another variable. Let's call that x. So we have the equation 100+x = 149, which is the same as x+100 = 149. We subtract 100 from both sides to undo the +100.14) After following the steps in problem 13, you should have (n-2)^2 = 49, which then becomes n-2 = 7 or n-2 = -7 after applying the square root to both sides. Those two equations solve to n = 9 and n = -5 in that order.f(x) = -x + 4 and g(x) = 6x + 3, find (f(x) - g(x))
A. -5x-1
B. 5x +1
C. -7x +1
Answers
Answer:
C
Step-by-step explanation:
f(x) - g(x)
= - x + 4 - (6x + 3)
= - x + 4 - 6x - 3 ← collect like terms
= - 7x + 1 → C
Write 65/22 as a decimal. If necessary, use a bar to indicate which digit or group of digits repeats.
Answers
Answer:
2.954545454
Step-by-step explanation:
65/22 = 65 divided by 22. That is how many times 22 can go into 65
A decimal number has a decimal point in it. That is a whole number and some fraction that could be in tenths or otherwise.
65 is the numerator,
22 is the denominator
Using a calculator
65/22 = 2.9545454
10
Select the correct answer.
Which equation is equivalent to the given equation?
- 4(x - 5) + 8x = 91 - 3
OA -5x = 2
OB. 5 = 17
OC. -5x = -23
OD. 5x = -12
Recet
Next
Answers
The equation that is equivalent to the given equation is 4x = 68. No answer is correct
Equations and expressionsEquations are two expressions equated to each other. Given the equation below;
- 4(x - 5) + 8x = 91 - 3
Expand
-4x + 20. + 8x = 88
Collect the like terms
4x + 20 = 88
4x = 88 - 20
4x = 68
Hence the equation that is equivalent to the given equation is 4x = 68
Learn more on equation here:https://brainly.com/question/2972832
#SPJ1
Can anyone help me ? It’s due in 20 minutes

Answers
Answer:
area of square = 100
area of circle = 15.7
the area of the shaded = im not really sure but im thinking its 50
Step-by-step explanation:
so u see the line in the middle it say 10 cm and the square is equal on all sides so it would be 10cm for the lenth and with so it would be 10 times 10 witch is 100 and u would use the 10 for the circle aswell witch u would use 3.14 times 10 divided by 2 to get the area of the circle
Answer:
The Area of the square is 100cm^2
The Area of the Circle is 78.54cm^2
The Area of the Yellow is 21.46cm^2
Step-by-step explanation: