share £84 in the ratio 6:3:3​

Answer:

3(4m - 3n)

Step-by-step explanation:

\(12m - 9n\)

\( = 3(4m - 3n)\)

Answer:

Guava has the most, Nelli juice has second most, Mango juice has third most Papaw juice has 4th most, Woodaple has the least

Step-by-step explanation:

Answer:

From smallest portion to biggest

Wood apple juice,

Papaw juice,

Mango juice,

Nelli Juice

Step-by-step explanation:

By looking at this graph we cam tell Guava juice has the most since it has the biggest section.

Now we can tell Wood apple juice isn't a popular option because it has the smallest section

Now to fill in the gaps, Papaw juice has the second least amount, then Nelli has third least amount, and and Guava Juice has the most.

option A

hope it really helps...!!!

The value of 'd' in terms of 'c' is 5c - 9. Therefore, the correct answer is F. 5c - 9.

Let's break down the given information step by step and try to find the value of 'd' in terms of 'c.'

According to the problem, Matt has 'c' baseball cards, and Jen has 'd' baseball cards. We are also given that Jen has 9 fewer than 5 times as many cards as Matt.

If we translate this information into an equation, it would look like:

d = 5c - 9

To understand how we arrived at this equation, let's break it down further:

Jen has 5 times as many cards as Matt: 5 * c

Jen has 9 fewer cards than 5 times Matt's cards: 5c - 9

So, the value of 'd' in terms of 'c' is 5c - 9.

Therefore, the correct answer is F. 5c - 9.

for such more question on value

https://brainly.com/question/22008756

#SPJ8

The inverse of 2 modulo 17 is 9.

To find an inverse of 2 modulo 17 by inspection, we have to try the values one by one like in hit and trial.

To do it by inspection, we shall multiply 2 with a number to get an answer 1 modulo 17. This means we have to find a number n such that:

\($n * 2 \equiv 1 \pmod {17}$\)

Let us try to multiply 2 with all the numbers 1 to 16 to find the inverse of 2 modulo 17:

\($2*1 = 2$\)  (mod 17)

\($2*2 = 4$\)  (mod 17)

\($2*3 = 6$\)  (mod 17)

\($2*4 = 8$\) (mod 17)

\($2*5 = 10$\) (mod 17)

\($2*6 = 12$\) (mod 17)

\($2*7 = 14$\) (mod 17)

\($2*8 = 16$\) (mod 17)

\($2*9 = 1$\) (mod 17)

\($2*10 = 3$\) (mod 17)

\($2*11 = 5$\) (mod 17)

\($2*12 = 7$\) (mod 17)

\($2*13 = 9$\) (mod 17)

\($2*14 = 11$\) (mod 17)

\($2*15 = 13$\) (mod 17)

\($2*16 = 15$\) (mod 17)

Since \($2 * 9 ≡ 1 \pmod{17}$\), the inverse of 2 modulo 17 is 9.

Therefore, the inverse of 2 modulo 17 is 9.

To know more about inverse refer here:

https://brainly.com/question/26257987#

#SPJ11

The proof for each theorem is matched as;

<EFC is a right angle: Definition of a right angle

m<EFC = 90; Definition of a tangent line

m<EFC + m<FEC + m<ECF = 180 degrees; triangle sum theorem

90 + m<FEC + m<ECF = 180; substitution property of equality

m<FEC + m<ECF = 90; substitution property of equality

m<FEC + m<ECF = definition of complementary angles

To determine the values, we need to know the following;

Learn more about angles at: https://brainly.com/question/25716982

#SPJ1

The value of the function g⁻¹(x) and f(x) will be equal. Then the value of x  will be 3.3.

A function is a statement, rule, or law that establishes the connection between two variables. In mathematics, functions are everywhere and are necessary for constructing physical connections.

The functions are given below.

f(x) = 3x - 7 and g(x) = x + 2/5

Then the inverse function of g(x) will be

x = g⁻¹(x) + 2/5

g⁻¹(x) = x - 2/5

Then we have

g⁻¹(x) = f(x)

Then the value of x will be

x - 2/5 = 3x - 7

 3x - x = 7 - 2/5

      2x = 33 / 5

        x = 33/10

        x = 3.3

More about the function link is given below.

https://brainly.com/question/5245372

#SPJ1

You have a mistake in the first step, you should distribute the 2 first, or divide by two, and after that you can follow the procedure as you were doing. Do you understand it?

w=8 is the answer

I can't asnwer more than one question per session, please begin a new session

Have a great day, please begin a ne

Answer:

the answer is b

Step-by-step explanation:

12:

Step-by-step explanation:

The limit of the sequence is 5/2. Note that we cannot use the ratio test for divergence since the limit of the ratio as n approaches infinity is not greater than 1. Therefore, the sequence does not diverge.

To determine the limit of the given sequence, we can use the fact that the leading terms in both the numerator and denominator have the same degree (n^2). Therefore, we can use the ratio of the leading coefficients (5/2) to find the limit as n approaches infinity. This gives us:
lim a(n)→[infinity]a(n) = lim (5n^2+n+2)/(2n^2-3)
= lim (5 + 1/n + 2/n^2) / (2 - 3/n^2)  (dividing both numerator and denominator by n^2)
= 5/2
Therefore, the limit of the sequence is 5/2.
Note that we cannot use the ratio test for divergence since the limit of the ratio as n approaches infinity is not greater than 1. Therefore, the sequence does not diverge.

To know more about limit visit :

https://brainly.com/question/12211820

#SPJ11

In this study, one individual refers to a single third-grade student from the total population of third graders in the school.

The student collected information on the number of siblings for each member of her class, which consists of 22 students. However, to consider the entire population, we need to take into account all the third-grade classes in the school. Since the school has five different third-grade classes, the population of interest comprises all the third graders across these five classes.

Each student in the population is considered an individual for the study. Therefore, one individual in this context refers to any random third-grade student from the school, regardless of the specific class they belong to. To conduct a comprehensive study and obtain accurate information about the number of siblings among third graders in the school, it would be necessary to collect data from a representative sample across all the third-grade classes.

By doing so, researchers can make inferences and draw conclusions about the entire population of third graders in the school based on the collected data.

Learn more about data here: brainly.com/question/28285882

#SPJ11

Answer:

Blue chairs

Step-by-step explanation:

To get the unit rate of red chairs, you simply divide 22.78/2, which equals $11.39

So the unit rate of RED chairs is $11.39

To get the unit rate of the blue chairs, you simply divide 67.80/6 which equals $11.30

So the unit rate of BLUE chairs is $11.30

Unit rate is simply the cost of one item (in this case chairs) the unit rate stays the same. If we flipped the operation on blue chairs and did 11.30*6, it equals $67.80. The same goes for the red chairs, if we did 11.39*2 it equals $22.78.

Hope this helps!

The largest possible value of p = 130

What is Integer?

Zero, a positive natural number, or a negative integer denoted by a minus sign are all examples of integers. The inverse additives of the equivalent positive numbers are the negative numbers. The boldface Z is a common way to represent the set of integers in mathematical terms.

Given,

2mnp = (m + 2) (n+2)(p+2)

lets first solve p

⇒(2mn)p = p((m + 2) (n+2) + 2 (m+2)(n+2)

⇒[2mn-(m+2)(n+2)p

=2(m+2)(n+2)

⇒p = \(\frac{2 (m+2)(n+2)}{mn-2n-2m-4}\)

⇒p = \(\frac{2(m+2)(n+2)}{(m-2)(n-2)-8}\)

Since it is obvious that we wish to reduce the denominator, we test (m-2)(n-2) - 8 = 1.

(m-2)(n-2) = 9. The pairs of 9 that can exist are (1, 9) (3,3). The results are, correspondingly, m = 3, n = 11, and m = 5, n = 5.

When we substitute the first pair into the numerator, we get 130, whereas the second pair gets 98. We now verify that 130 is the best value, setting a=m-2 and b=n-2 to facilitate calculations.

Since,         0 ≤(a-1)(b-1) ⇒ a+b≤ab+1

we have,  

p = \(\frac{2(a+4)(b+4)}{ab-8}\)

= \(\frac{2ab+8(a+b++32}{ab-8} \leq \frac{2ab+8(ab+1)+32}{ab-8}\)

= 10 +\(\frac{120}{ab-8}\)≤130

Where we see (m,n)=(3,11) gives us our maximum value of 130

Remember that 0 ≤ (a-1)(b-1) assumes m,n ≥3, but there is clear as \(\frac{2m}{m+2}\) = \(\frac{(n+2)(p+2)}{np}\) > 1 and similarly for n

we state the denominator differently as we solve for p.

p = \(\frac{2(m+2)(n+2)}{(m+2)(n+2)-4(m+n+2)}\)  ⇒\(\frac{1}{p}\) = \(\frac{1}{2}\) - \(\frac{2(m+n+2)}{(m+2)(n+2)}\)

Here it suffices to maximise \(\frac{m+n+2}{(m+2)(n+2)}\) under the conditions that p is a positive integer.

Then, m+n+2/(m+2)(n+2) > 1/2 for m = 1,2, we fix m =3

⇒ 1/p = 1/2-\(\frac{2(n+2)}{5(n+2)}\)

= n-10/10(n+2)

where we let n=11 to achieve p = 130

The largest possible value is 130

To learn more about integer visit:

brainly.com/question/15276410

#SPJ4

We want to find the height of the dollhouse's front door.

Since the dollhouse's measures is given in inches, we have just two possible right choices:

because the answer should be given in inches.

If the correct option were the third one, 14 in,

then the real door measure would be twice in feet: 28 feet.

If the correct option were the first one, 3 1/2 in,

then the real door measure would be twice in feet: 7 in.

28 feet is a really big door. It is more likely for a house to have a 7 in door.

Answer:  W = 20 1/3, L = 7 2/3 cm

Step-by-step explanation:

Width, W, is 5 cm more than twice the length of the perimeter.

Perimeter = 2W + 2L

W = 2L+5

Perimeter is 56cm:

56 cm = 2W + 2L

Substitute W = 2L + 5 for W:

56 cm = 2W + 2L

56 cm = 2(2L+5) + 2L

56 cm = 4L + 10 + 2L

6L = 46 cm

L = 7 2/3 cm

Since W = 2L + 5

W = 2(7 2/3) + 5

W = 2 (23/3) + 5

W = 46/3 + 5

W = 15 1/3 + 5

W = 20 1/3

2W + 2L = P?

2(20 1/3) + 2(7 2/3) =56 ?

40 2/3 + 15 1/3 = 56?

56 = 56  YES

Answer:

Ms. Lesure is going to need to buy 4 pizzas for Mr. Shows Interactions A class. The boys would eat 20 slices and the Girls in total will eat 12 slices. In total you'll need about 32 slices and 32 divided by 8 is 4.

Step-by-step explanation:

The correct answer is (a). fail to reject the null hypothesis at null= 0.05 and all larger null.

The null hypothesis (H0) in this case is that β1=0, meaning that there is no relationship between the independent and dependent variables in the regression study.

The alternative hypothesis (Ha) is that β1≠0, meaning that there is a relationship between the independent and dependent variables.

The 95% confidence interval for β1 is (-5.65, 2.61). This means that we are 95% confident that the true value of β1 falls within this range. Since the range includes 0, we cannot reject the null hypothesis that β1=0.

Therefore, we fail to reject the null hypothesis at a significance level of 0.05 (null=0.05) and all larger significance levels.

In other words, there is not enough evidence to suggest that there is a relationship between the independent and dependent variables in the regression study, so we cannot reject the null hypothesis.

Hence, fail to reject the null hypothesis at null=0.05 and all larger null is the correct answer, i.e., option (a)

To know more about the null hypothesis, refer here:

https://brainly.com/question/17018373#

#SPJ11

The quadratic equations are given as follows:

37. y = 1.6(x² - 2x - 3).

38. y = x² - x.

39. y = 0.4074(x² - 12x + 11).

The roots of the quadratic equation are at x = -1 and x = 3, hence it can be written as follows:

y = a(x + 1)(x - 3)

In which a is the leading coefficient.

Hence:

y = a(x² - 2x - 3)

When x = 1, y = -8, hence the leading coefficient a can be found as follows:

-8 = a(1 - 2 - 3)

5a = 8

a = 8/5

a = 1.6

Hence the equation is:

y = 1.6(x² - 2x - 3).

The roots of the quadratic equation are at x = 0 and x = 1, hence it can be written as follows:

y = ax(x - 1)

Hence:

y = a(x² - x)

When x = 2, y = -2, hence the leading coefficient a can be found as follows:

2 = a(2² - 2)

2a = 2

a = 1.

Hence the equation is:

y = x² - x.

The roots of the quadratic equation are at x = 1 and x = 11, hence it can be written as follows:

y = a(x - 1)(x - 11)

Hence:

y = a(x² - 12x + 11)

When x = 2, y = -11/3, hence the leading coefficient a can be found as follows:

-11/3 = a(4 - 24 + 11)

9a = 11/3

a = 11/27

a = 0.4074.

Hence the equation is:

y = 0.4074(x² - 12x + 11).

More can be learned about quadratic equations at https://brainly.com/question/24737967

#SPJ1

(a) The solutions for x* and y* are given by equations (6) and (7), respectively. (b) When I = $24, Pₓ = $4, and Pᵧ = $2, the optimal values of x* and y* are x* = 16 and y* = 20, respectively.

(a) To solve for x* and y* in terms of Pₓ, Pᵧ, and I, we need to find the utility-maximizing bundle that satisfies the budget constraint.

The utility function is given as U(x, y) = x^(1/2) * y^(1/2).

The budget constraint is expressed as Pₓ * x + Pᵧ * y = I.

To maximize utility, we can use the Lagrange multiplier method. We form the Lagrangian function L(x, y, λ) = U(x, y) - λ(Pₓ * x + Pᵧ * y - I).

Taking the partial derivatives of L with respect to x, y, and λ and setting them equal to zero, we get:

∂L/∂x = (1/2) *\(x^(-1/2) * y^(1/2)\)- λPₓ = 0   ... (1)

∂L/∂y = (1/2) *\(x^(1/2) * y^(-1/2)\) - λPᵧ = 0   ... (2)

∂L/∂λ = Pₓ * x + Pᵧ * y - I = 0               ... (3)

Solving equations (1) and (2) simultaneously, we find:

\(x^(-1/2) * y^(1/2)\)= 2λPₓ   ... (4)

\(x^(1/2) * y^(-1/2)\)= 2λPᵧ   ... (5)

Dividing equation (4) by equation (5), we have:

\((x^(-1/2) * y^(1/2)) / (x^(1/2) * y^(-1/2))\) = (2λPₓ) / (2λPᵧ)

y/x = Pₓ/Pᵧ

Substituting this into equation (3), we get:

Pₓ * x + (Pₓ/Pᵧ) * x - I = 0

x * (Pₓ + Pₓ/Pᵧ) = I

x * (1 + 1/Pᵧ) = I

x = I / (1 + 1/Pᵧ)        ... (6)

Similarly, substituting y/x = Pₓ/Pᵧ into equation (3), we get:

Pᵧ * y + (Pᵧ/Pₓ) * y - I = 0

y * (Pᵧ + Pᵧ/Pₓ) = I

y * (1 + 1/Pₓ) = I

y = I / (1 + 1/Pₓ)        ... (7)

Therefore, the solutions for x* and y* are given by equations (6) and (7), respectively.

(b) Given I = $24, Pₓ = $4, and Pᵧ = $2, we can substitute these values into equations (6) and (7) to find the values of x* and y*.

x* = 24 / (1 + 1/2) = 16

y* = 24 / (1 + 1/4) = 20

So, when I = $24, Pₓ = $4, and Pᵧ = $2, the optimal values of x* and y* are x* = 16 and y* = 20, respectively.

Learn more about partial derivatives here:

https://brainly.com/question/32387059

#SPJ11

Suppose U(x,y)=x  1/2  y  1/2  and P  x ​  x+P  y ​  y=I a. Solve for x  ∗  (P  x ​  ,P  y ​  ,I) and y  ∗  (P  x ​  ,P  y ​  ,I). b. What are the values of x  ∗  (P  x ​  ,P  y ​  ,I) and y  ∗  (P  x ​  ,P  y ​  ,I) if I=$24,P  x ​  =$4 and,P  y ​  =$2?

Answer:

  3 + 2 × (8 - 7) ÷ 1

Step-by-step explanation:

You want to fill in math operations to make the expression 3 _ 2 _ (8 _ 7) _ 1 equal to 5, using +, -, ×, and ÷ once each.

It is unlikely that ÷ will go between 3 and 2, because that would give a fraction not easily modified to give a value of 5.

It is likely that + or - goes inside the parentheses, as there would be no need for parentheses if that operation were × or ÷. The minus sign seems more appropriate, since adding 8 and 7 would give 15, a value not easily modified to make 5.

Using - inside parentheses reduces the problem to ...

  3 _ 2 _ 1 _ 1 = 5 . . . . . with available remaining operators: +, ×, ÷

It seems appropriate to make this be ...

  3 + 2 = 5 . . . . . . uses the + operation in the first blank

which requires that 2 _ 1 _ 1 = 2 using × and ÷. We can only use them in that order if we want the value 2: 2 × 1 ÷ 1 = 2

The desired expression is ...

  3 + 2 × (8 - 7) ÷ 1 = 5

Answer:

3 + 2 ÷ (8 - 7) × 1 = 5

Step-by-step explanation:

There is likely more than one way to do this problem.

Here's one way:

3 + 2 ÷ (8 - 7) × 1 = 5

Do parenthesis first.

3 + 2 ÷ (1) × 1 = 5

Multiply or divide in order from left to right.

3 + 2 × 1 = 5

3 + 2 = 5

Lastly, add.

5 = 5

So, this checks out.

One possible answer is:

3 + 2 ÷ (8 - 7) × 1 = 5

Cost of tjhe donut: D

Cost of the large coffee: C

On Monday Harold picked up six donuts and two large coffees for the office staff, he paid $5.80:

On Tuesday, Melinda picked up four donuts and 5 large coffees for the office staff. She paid $7.02:

Use the next system of linear equations to find the value of D and C:

1. Solve D in the first equation:

2. Substitute the D in the second equation by the equation you get in step 1:

3. Solve C:

4. Use the value of C=0.86 to find D;

The solution fot the system is:

Step-by-step explanation:

correct correct answer of this question is option d x equals to 4

please mark my answer as brain list and also vote me

Based on the properties of the diagonals of a parallelogram, the value of x that makes the quadrilateral a parallelogram is: x = 4.

The diagonals of a parallelogram bisects each other into equal segments.

Therefore, we would have:

AE = CE

Substitute

5x + 28 = 3x + 36

5x - 3x = -28 + 36

2x = 8

x = 8/2

x = 4

Learn more about the diagonals of a parallelogram on:

https://brainly.com/question/3050890

#SPJ2

The exact value  of \(sin 2x\) is \(4√5/9.\)

Given that \(sec x = 3/2 and csc y = 3\)where x and y are in the 2x = 2 sin x quadrant, we need to find the exact value of sin 2x.

In the first quadrant, we have the following values of the trigonometric ratios:\(cos x = 2/3 and sin y = 3/5\)

Also, we know that sin \(2x = 2 sin x cos x.\)

Now, we need to find sin x.

Having sec x = 3/2, we can use the Pythagorean identity

\(^2x + 1 = sec^2xtan^2x + 1 = (3/2)^2tan^2x + 1 = 9/4tan^2x = 9/4 - 1 = 5/4tan x = ± √(5/4) = ± √5/2\)

As x is in the first quadrant, it lies between 0° and 90°.

Therefore, x cannot be negative.

Hence ,\(tan x = √5/2sin x = tan x cos x = √5/2 * 2/3 = √5/3\)

Now, we can find sin 2x by using the value of sin x and cos x derived above sin \(2x = 2 sin x cos xsin 2x = 2 (√5/3) (2/3)sin 2x = 4√5/9\)

Therefore, the exact value  of sin 2x is 4√5/9.

To know more about trigonometric visit :

https://brainly.com/question/29156330

#SPJ11

(A) The scale factor of the dilation that transforms Triangle PQR to Triangle P'Q'R'  is 1/2

(B) Coordinates of Δ P"Q"R"

P" (-4,0)

Q"(-3,1)

R"(1,-2)

(C) Triangles PQR and P"Q"R" are not congruent.

Given

ΔPQR is transformed into ΔP'Q'R'

Coordinates of P, Q, R are

P (8,0),

Q(6,2)

R(-2,-4)

Coordinates of P'Q'R' are

P′(4, 0)

Q′(3, 1)

R′(−1, −2)

(A) By Distance formula we can find the distance between P Q and P'Q'

Distance formula = \(D = \sqrt{(x2-x1)^{2} +(y2-y1)^{2} }\)

Where D = Distance between two points

from distance formula we can write that

PQ = \(\sqrt{(6-8)^{2} +(2-0)^{2} } = \sqrt{4+4} =2 \sqrt{2}\)

Similarly

P'Q'= √2

PQ /P'Q' = 2

hence the scale factor of dilation is 1/2 (Compression)

(B )The Coordinates of Reflection about y axis can be written for a point

(x,y) as (-x,y)

So the Coordinated of Δ P"Q"R" can be written as

P" (-4,0)

Q"(-3,1)

R"(1,-2)

(C) ΔPQR  and ΔP"Q"R" are similar triangles but they are not  congruent because their sides  are not equal in size.

Learn more about Congruent triangles at:

brainly.com/question/12413243

#SPJ1

y=-2x(squared)+3x-7

the 2x is squared

hope that helped

Answer:

Step-by-step explanation: So you want to know what the graph is explaining? It probably means that the company on the top makes the most money. It is a comparison of how much money the different companies make.

Step-by-step explanation:

5(1-2x) = -65

5-10x = -65

65+5 = 10x

70 = 10x

7 = x

x = 7

Answer:

X=7/2

Step-by-step explanation:

5(1 - 2x) = -65

5-20x=-65

-20x=-65-5

-20x=-70

Minus sign cancel from both side

So x=70/20

X=7/2

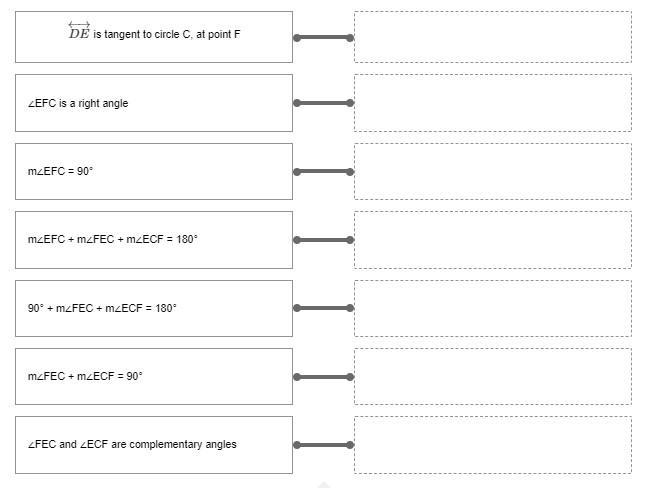
Answer:

?

Step-by-step explanation:

with what

Answer:

120

Step-by-step explanation:

I got 120 because the width of the diamonds are 30. (180 - 150)

We can make sure that is correct by checking all the other pyramids.

anyways, we have 30 60 90 120 150 for all our pyramids. So the answer is indeed

120

Answer:

b

Step-by-step explanation: