Seventeen out of 20 teens said they eat breakfast every morning. What is the reasonable prediction for the number of teens out of 1,280 who eat breakfast every morning?
A.
340
B.
940
C.
1088
D.
1260
Answers
Answer:
It would be 1,088/1,280
Step-by-step explanation:
The answer is 1,088
Related Questions
15 people on a softball team show up for a game. ch 06 sec 3 ex 28 (a) - combinations & permutations how many ways are there to choose 10 players to take the field?
Answers
There are 3,003 ways to choose 10 players out of 15 people to take the field.
There are different ways to approach this problem, but one common method is to use the combination formula.
The number of ways to choose 10 players out of 15 is given by the formula, where C(n, r) represents the number of combinations of k items that can be selected from a set of n items.
\(^{n}C_{r} =^{15}C_{10}\)
= \(\frac{15!}{(15-10)!.10!}\)
= \(\frac{15!}{(5)!.10!}\)
= 15 x 14 x 13 x 12 x 11 / 5 x 4 x 3 x 2 x 1
= 3,003 ways.
Therefore, there are 3,003 ways to choose 10 players out of a team of 15 players to take the field.
To know more about combination
https://brainly.com/question/15416346
#SPJ4
The rectangle shown has a perimeter of 148 cm and the given area. Its length is 8 more than five times its width. Write and solve a system of equations to find the dimensions of the rectangle.
Answers
Answer:
System of equations:
L = 5W + 7
2W + 2L = P
L = 62 cm
W = 11 cm
Step-by-step explanation:
Given the measurements and key words/phrases in the problem, we can set up two different equations that can be used to find both variables, length and width, of the rectangle.
The formula for perimeter of a rectangle is: 2W + 2L = P, where W = width and L = length. We also know that the L is '7 more than five times its width'. This can be written as: L = 5W + 7. Using this expression for the value of 'L', we can use the formula for perimeter and solve for width:
2W + 2(5W + 7) = 146
Distribute: 2W + 10W + 14 = 146
Combine like terms: 12W + 14 = 146
Subtract 14 from both sides: 12W + 14 - 14 = 146 - 14 or 12W = 132
Divide 12 by both sides: 12W/12 = 132/12 or W = 11
Put '11' in for W in the equation for 'L': L = 5(11) + 7 or L = 55 + 7 = 62.
pls anwserr my quiz accurite NO EXPLIMATON PLS

Answers
can y’all help me ? a,b,c,d,e or f plsss like rn

Answers
Answer:
b and d
Step-by-step explanation:
there is two answers
HELP PLEASE!! is math 20 points

Answers
Answer:
0x = 0y0
0x = 2yx = 2y/0 = 0
2x = 2yx = 2y/2 = y
4x = 3yx = 3y/4
HOPE THIS HELPS YOU
Follw me = 10 thanks
Mark as brainliest = 10 thanks
1 thanks to me = 2 thanks
Mr. Swift is traveling from his house to the history museum. How many meters will he travel to the museum?
Answers
If Mr. Swift is traveling from his house to the history museum. The number of meters will he travel to the museum is 6,400 meters.
Number of metersGiven:
Distance=6.4 Kilometres
Hence:
1 kilometre= 1,000 meters
Number of meters=6.4 kilometres x 1,000 meters
Number of meters =6,400 meters
Therefore the number of meters will he travel to the museum is 6,400 meters.
Learn more about number of meters here:https://brainly.com/question/870330

please show me step by step i am very confused
In 2010, there were 1690 state parks in the USA. By 2017, there were 1760 state parks. The growth of state parks was linear. Write a function equation with \( p(x)= \) the number of state parks in the
Answers
The given information shows that there were 1690 state parks in the year 2010, and by the year 2017, the number of state parks increased to 1760. Also, it's mentioned that the growth of state parks was linear.The linear equation is defined as `y= mx + c`, where m is the slope and c is the y-intercept.
In this case, let's assume that x is the number of years, and p(x) is the number of state parks present in that year.Since the equation is linear, the slope can be calculated using the given information:
Slope, `m = (y₂ - y₁) / (x₂ - x₁)
`Here, `y₂ = 1760`, `y₁ = 1690`, `
x₂ = 2017`, and `x₁ = 2010`
.Substituting the values in the above formula, we get:
Slope, `m = (1760 - 1690) / (2017 - 2010)`
= 70 / 7= 10
Now, we know the slope of the equation. We also know that in the year 2010, there were 1690 state parks. Therefore, the y-intercept, c = 1690 Substituting the values of slope and y-intercept in the equation
`y = mx + c`, we get the function equation: `
p(x) = 10x + 1690`.
`p(x) = 10x + 1690`
There were 1690 state parks in the year 2010, and by the year 2017, the number of state parks increased to 1760. Also, it's mentioned that the growth of state parks was linear.The linear equation is defined as `y= mx + c`, where m is the slope and c is the y-intercept. In this case, let's assume that x is the number of years, and p(x) is the number of state parks present in that year.Since the equation is linear, the slope can be calculated using the given information:
Slope, `m = (y₂ - y₁) / (x₂ - x₁)`
Here, `y₂ = 1760`,
`y₁ = 1690`, `x₂ = 2017`,
and `x₁ = 2010
`.Substituting the values in the above formula, we get:Slope,
`m = (1760 - 1690) / (2017 - 2010)`
= 70 / 7= 10
Now, we know the slope of the equation. We also know that in the year 2010, there were 1690 state parks. Therefore, the y-intercept, c = 1690Substituting the values of slope and y-intercept in the equation `
y = mx + c`,
we get the function equation:
`p(x) = 10x + 1690`.
To know more about equation visit:
https://brainly.com/question/29657983
#SPJ11
a drawing of an arrow was made using a square and a triangle what is the area of the drawing of the arrow in square feet
Answers
Given data:
The given figure is shown.
The area of the composite figure is,
\(\begin{gathered} A=(4\text{ ft)(4 ft)+}\frac{1}{2}(\text{4 ft+1.5 ft+1.5 ft)(}6\text{ ft)} \\ =(16+21)ft^2 \\ =37ft^2 \end{gathered}\)Thus, the area of the given figure is 37 sq-feet, so first option is correct.
Write the coordinates of the vertices after a reflection over the y-axis

Answers
The most appropriate choice for reflection will be given by-
After reflection over y-axis, coordinate of K will become K' (6, -1)
After reflection over y-axis, coordinate of L will become L' (0, -1)
After reflection over y-axis, coordinate of M will become M' (0, -2)
After reflection over y-axis, coordinate of J will become J' (6, -2)
What is reflection?
Reflection of a figure about a line is a transformation in which a mirror image of the figure can be obtained over the line.
The line is called the line of reflection.
Here,
After reflection over the y - axis, sign of x coordinate will be same.
Coordinate of K = (-6, -1)
After reflection over y-axis, coordinate of K will become K' (6, -1)
Coordinate of L = (0, -1)
After reflection over y-axis, coordinate of L will become L' (0, -1)
Coordinate of M = (0, -2)
After reflection over y-axis, coordinate of M will become M' (0, -2)
Coordinate of J = (-6, -2)
After reflection over y-axis, coordinate of J will become J' (6, -2)
To learn more about reflection, refer to the link-
brainly.com/question/26642069
#SPJ13
Locate all local maxima, local minima, and saddle points (if exist) of the function \[ f(x, y)=x^{2}+y^{2}+\frac{2}{x y} . \]
Answers
.Let's calculate the second-order partial derivatives of f(x, y).∂²f/∂x² = 2/xy²³[1]∂²f/∂y² = 2/x²y³[2]∂²f/∂x∂y
= –2/xy³[3]
At the critical point (1, 1), we have:∂²f/∂x² = 2,
∂²f/∂y² = 2,
and ∂²f/∂x∂y = –2.
So, Δ = ∂²f/∂x² × ∂²f/∂y² – (∂²f/∂x∂y)²
= (2 × 2) – (–2)²
= –4 < 0
Therefore, (1, 1) is a saddle point.
At the critical point (–1, –1), we have:∂²f/∂x² = –2
, ∂²f/∂y² = –2,
∂²f/∂x∂y = –2.
So, Δ = ∂²f/∂x² × ∂²f/∂y² – (∂²f/∂x∂y)²
= (–2 × –2) – (–2)²
= 0
Therefore, we can't conclude anything by this test.
At the critical point (–1, 1),
we have:∂²f/∂x² = –2,
∂²f/∂y² = 2, and
∂²f/∂x∂y = 2.
So, Δ = ∂²f/∂x² × ∂²f/∂y² – (∂²f/∂x∂y)²= (–2 × 2) – (2)²
= –8 < 0
Therefore, (–1, 1) is a saddle point.At the critical point (1, –1), we have:
∂²f/∂x² = 2,
∂²f/∂y² = –2, and
∂²f/∂x∂y = –2
.So, Δ = ∂²f/∂x² × ∂²f/∂y² – (∂²f/∂x∂y)²
= (2 × –2) – (–2)²
= –8 < 0
Therefore, (1, –1) is a saddle point.
Therefore, the given function has three saddle points.
To know more about equation visit :-
https://brainly.com/question/11624077
#SPJ11
2.5 divided by 3,321.2?
Answers
Answer:
0.000752739974
by the way i used a calculator
I hope this helps :)
An airplane is flying at an elevation of 15,000 feet. The airport is 6 miles away from a point directly below the airplane on the ground. How far is the airplane from the airport?
Answers
Answer:
The distance between the airplane and the airport is:
\(c=6.64\: miles\)
Step-by-step explanation:
We can use the Pythagoras theorem to find the distance from the airplane to the airport.
The equation is:
\(c^{2}=a^{2}+b^{2}\)
Where:
a represents the elevations of the airplane (15000 feet)b is the distance from the ground directly below the airplane to the airport (6 miles)c is the distance between the airplane and the airport.We need first to convert 15000 feet in miles.
\(15000\: feet \times \frac{0.00019\: miles}{1\: feet}=2.85\: miles\)
Therefore, c will be:
\(c^{2}=a^{2}+b^{2}\)
\(c=\sqrt{a^{2}+b^{2}}\)
\(c=\sqrt{2.85^{2}+6^{2}}\)
\(c=6.64\: miles\)
I hope it helps you!
Two friends want to find out the distance across a creek. Friends A holds one end of a rope and is standing (2x^2+2x-2) feet from the creek blank. Friend B holds the other end of the rope and is standing (x^2+17) feet from the creek bank. If the rope the friends are holding is (6x^2-x+12 feet long, how wide is the creek?
Answers
Two buddies want to know how far a creek is across. The creek is (3x² - 3x - 3) feet wide.
We know the distance of Friend A from one end of bank and distance of Friend B from another end of the bank and the distance between Friend A and B which is the distance of the rope and we have to calculate the width of the creek.
Distance of rope = Distance of friend A from the one end of the bank + width of creek + distance of Friend B from another end of the bank
6x²- x + 12 = (2x²+2x-2) + width of the creek + (x²+17)
6x²- x + 12 = width of the creek + (2x²+ 2x - 2 + x² + 17)
6x²- x + 12 = width of the creek + ( 3x² + 2x + 15)
width of the creek = 6x²- x + 12 - ( 3x² + 2x + 15)
= 6x²- x + 12 - 3x² - 2x - 15
= 3x² - 3x - 3
To know more about distance:
https://brainly.com/question/23985885
#SPJ1
Please help! Correct answer only!
In a carnival game, there is a machine that will shuffle a deck of 50 cards numbered from 1 to 50 and then spit one card out. If the number on the card is odd, you win $15. If the number on the card is even, you win nothing. If you play the game, what is the expected payoff?
$___

Answers
Answer:
$7.50
Step-by-step explanation:
Since there is a 50% chance that the card is odd, the expected payoffs would be $15 * 50%=0.5*15=7.5. Hope this helps!
public class BinarySearch \{ public static void main(Stringll args) f int [1]yl ist ={1,2,3,7,10,12,20}; int result = binarysearch ( inylist, 20); if (result =−1 ) System, out, println("Not found:"); else System.out.println("The index of the input key is " + result+ ". "): y public static int binarysearch(int]l List, int key) \{ int low =0; int high = iist. length −1 while (high >= low) \& int mid =( low + high )/2; if (key < List [mid] high = mid −1; else if (key =1 ist [ mid ] ) return inid; else low = mid +1; return −1; // Not found \} l TASK 4: Binary Search in descending order We have learned and practiced the implementation of the binary search approach that works on an array in ascending order. Now let's think about how to modify the above code to make it work on an array in descending order. Name your new binary search method as "binarysearch2". Implement your own code in Eclipse, and ensure it runs without errors. Submit your source code file (.java file) and your console output screenshot. Hint: In the ascending order case, our logic is as follows: int mid =( low + high )/2 if ( key < list [mid] ) else if (key = ist [mid]) return mid; In the descending order case; what should our logic be like? (Swap two lines in the above code.)
Answers
The task involves modifying the given code to implement binary search on an array in descending order. The logic of the code needs to be adjusted accordingly.
The task requires modifying the existing code to perform binary search on an array sorted in descending order. In the original code, the logic for the ascending order was based on comparing the key with the middle element of the list. However, in the descending order case, we need to adjust the logic.
To implement binary search on a descending array, we need to swap the order of the conditions in the code. Instead of checking if the key is less than the middle element, we need to check if the key is greater than the middle element. Similarly, the condition for equality also needs to be adjusted.
The modified code for binary search in descending order would look like this:
public static int binarysearch2(int[] list, int key) {
int low = 0;
int high = list.length - 1;
while (high >= low) {
int mid = (low + high) / 2;
if (key > list[mid])
high = mid - 1;
else if (key < list[mid])
low = mid + 1;
else
return mid;
}
return -1; // Not found
}
By swapping the conditions, we ensure that the algorithm correctly searches for the key in a descending ordered array.
For more information on array visit: brainly.com/question/30891254
#SPJ11
I need help I'm struggling on this problem

Answers
The factors of the polynomial f (x) = x^5 - 7x - 22x³ + 44x² - 104x + 288 that is true for f (9) = 0 are (x - 9) and (x⁴ + 2x³ - 4x² + 8x - 32).
Factor theorem of a polynomialThe factor theorem states that: if p(x) is divisible by x - a if and only if p(a)=0.
The polynomial expression x^5 - 7x - 22x³ + 44x² - 104x + 288 and f (9) = 0, then x - 9 = 0 is a factor. Applying long division as follows;
x^5 divided by x equals x⁴
x - 9 multiplied by x⁴ equals x^5 - 9x⁴
subtract x^5 - 9x⁴ from x^5 - 7x - 22x³ + 44x² - 104x + 288 will result to 2x⁴ - 22x³ + 44x² - 104x + 288
2x⁴ divided by x equals 2x³
x - 9 multiplied by 2x³ equals 2x⁴ - 18x³
subtract 2x⁴ - 18x³ from 2x⁴ - 22x³ + 44x² - 104x + 288 will result to -4x³ + 44x² - 104x + 288
-4x³ divided by x equals -4x²
x - 9 multiplied by -4x² equals -4x³ + 36x²
subtract -4x³ + 36x² from -4x³ + 44x² - 104x + 288 will result to 8x² - 104x + 288
8x² divided by x equals 8x
x - 9 multiplied by 8x equals 8x - 72x
subtract 8x - 72x from 8x² - 104x + 288 will result to - 32x + 288.
-32x divided by x equals -32
x - 9 multiplied by -32 equals -32x + 288
subtract -32x + 288 from- 32x + 288 will result to a remainder 0(zero).
We can then conclude the factors (x - 9) and (x⁴ + 2x³ - 4x² + 8x - 32) are the product of linear factors for the polynomial f (x) = x^5 - 7x - 22x³ + 44x² - 104x + 288 that makes it zero.
Learn more about polynomials here: https://brainly.com/question/24729294
#SPJ1
the event containing the outcomes belonging to a or b or both is the __________ of a and b.
Answers
The event containing the outcomes belonging to a or b or both is the union of a and b.
Let us consider two sets a and b, and say events or the elements in set a are: (x, y, z), and the elements in set b are: (o, p, q)
The union of these two sets will give:
aUb=(x, y, z, o, p, q)
Now, a union of two sets (denoted by U), for our case a and b, is the set or event containing the elements belonging to a or b or both the elements in a and b altogether.
Thus, the even containing the outcomes belonging to a or b or both in a and b altogether is the union of a and b.
Learn more about union of a set here:
https://brainly.com/question/23337676
#SPJ4
A product's quality characteristic has a specification (in inches) of $0.200 \pm 0.020$. If the value of the quality characteristic exceeds 0.200 by the tolerance of 0.020 on either side, the product will require a repair of $\$ 150$. The Taguchi loss function for this example is given by:
$L(x)=60(x-T)^2$
b. $L(x)=150(x-T)$
c. $L(x)=375,000(x-T)^2$
d. $L(x)=30(x-T)^2$
Answers
If the value exceeds\($0.200$\) by the tolerance of \($0.020$\) on either side, a repair cost of \($\$150$\)is incurred.
\($L(x) = 150(x - T)$\) option b.
The Taguchi loss function measures the cost or loss associated with deviations from a target value in a quality characteristic.
In this case, the specification for the quality characteristic is \($0.200 \pm 0.020$\).
If the value exceeds \($0.200$\) by the tolerance of \($0.020$\)on either side, a repair cost of $\$150$ is incurred.
Based on this information, the Taguchi loss function for this example is given by:
b.\($L(x) = 150(x - T)$\)
In the given options, option b represents the correct Taguchi loss function. The loss function is a linear function where the loss increases linearly with the deviation from the target value.
The coefficient of \($150$\) represents the cost of repair per unit deviation.
This loss function is appropriate for the given scenario as it accurately captures the cost associated with deviations from the target value.
The Taguchi loss function provides a quantitative measure to assess the impact of variations in the quality characteristic and helps in making decisions regarding process improvement and optimization.
In this case, it allows for evaluating the cost implications of exceeding the specified tolerance and guides decision-making on whether repairs are necessary based on the associated costs.
for such more questions on cost
https://brainly.com/question/2292799
#SPJ8
During the period from 2011 through 2015 the annual returns on small U.S. stocks were - 3.80 percent, 19.15 percent, 45.91 percent, 3.26 percent, and - 3.80 percent, respectively. What would a $1 investment, made at the beginning of 2011 , have been worth at the end of 2015 ? (Round answer to 3 decimol places, eg. 52.750.) Value in 2015$ What average annual return would have been earned on this investment? (Round answer to 2 decimai ploces, eg. 52.75) Average annual return percent per year:
Answers
The average annual return on this investment from 2011 to 2015 is approximately 0.8%.
To calculate the value of a $1 investment made at the beginning of 2011 and its average annual return by the end of 2015, we need to multiply the successive annual returns and calculate the cumulative value.
The successive annual returns on small U.S. stocks from 2011 to 2015 are:
-3.80%, 19.15%, 45.91%, 3.26%, and -3.80%.
To calculate the cumulative value, we multiply the successive returns by the initial investment value of $1:
(1 + (-3.80%/100)) * (1 + (19.15%/100)) * (1 + (45.91%/100)) * (1 + (3.26%/100)) * (1 + (-3.80%/100))
Calculating this expression, we find that the cumulative value is approximately $1.044, rounded to three decimal places.
Therefore, a $1 investment made at the beginning of 2011 would have been worth approximately $1.044 at the end of 2015.
To calculate the average annual return, we need to find the geometric mean of the annual returns. We can use the following formula:
Average annual return = (Cumulative value)^(1/number of years) - 1
In this case, the number of years is 5 (from 2011 to 2015).
Average annual return = (1.044)^(1/5) - 1
Calculating this expression, we find that the average annual return is approximately 0.008 or 0.8% per year, rounded to two decimal places.
Therefore, the average annual return on this investment from 2011 to 2015 is approximately 0.8%.
Learn more about compound interest here:
https://brainly.com/question/24274034
#SPJ11
help me pleaseeeeeee

Answers
Answer:
the slope is 3 3 .
Step-by-step explanation:
1. If a polynomial of Degree 4 has an imaginary zero at -2i and a real zero at 5, how many imaginary zeros does it have?
and how many real zeros does it have?
2. If a polynomial has a Degree of two, how many imaginary zeros could it have? and how many real zeros could it have?
Answers
Answer:
Complex roots for polynomials equations will always come in conjugate pairs. Since 1-2i is a root, 1+2i will also be a root. (Just switch the sign of the imaginary part to its opposite.)
Step-by-step explanation:
So far we have 1-2i and 1+2i as roots. We need two more to make a 4th degree polynomial.
x=1 with multiplicity of 2 means that we count the root twice when we write down the polynomial: (x - 1)(x - 1) = (x - 1)2
Putting it all together, we can construct our polynomial of degree 4 as
y = f(x) = (x - 1)(x - 1)[x - (1-2i)][x - (1+2i)]
Multiply the factors (FOIL):
[x - (1-2i)][x - (1+2i)] =
x2 - (1+2i)x - (1-2i)x + (1-2i)(1+2i) =
x2 - x - 2ix - x + 2ix + (1 + 2i - 2i + 4) =
x2 - 2x + 5
(x - 1)(x - 1) = x2 - x - x + 1 = x2 - 2x + 1
Now multiply the two underlined expressions:
y = (x2 - 2x + 5)(x2 - 2x + 1)
= x4 - 2x3 + 5x2 - 2x3 + 4x2 - 10x + x2 - 2x + 5 by multiplying term by term
= x4 - 4x3 + 10x2 -12x + 5 by collecting like terms.
Please help me with 37 and 38 with the correct answer

Answers
Answer:
The slope is 20x
The y-intercept is 175
Dan was thinking of a number. Dan adds 10 to it, then doubles it and gets an answer of 56.6. What was the original number
Answers
Answer:
23.3 is the answer to this question

a basket of fruits contains 5 apples and 3 pears. sharon took two fruits at random. what is the probability that both fruits are apples? write your answer in the simplest form of fraction
Answers
The probability that Sharon randomly selects two apples from the basket of fruits, given that there are 5 apples and 3 pears, can be expressed as a fraction.
To find the probability, we need to consider the total number of possible outcomes and the number of favorable outcomes.
The total number of possible outcomes is the number of ways Sharon can select any two fruits from the basket, which can be calculated using combinations. In this case, there are 8 fruits in total, so the total number of possible outcomes is C(8, 2) = 28.
The number of favorable outcomes is the number of ways Sharon can select two apples from the five available in the basket, which is C(5, 2) = 10.
Therefore, the probability that both fruits Sharon selects are apples is 10/28, which can be simplified to 5/14.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
martha invested $41.25 into a company. if each share was worth $1 1/4 how many shares did Martha invest in the company
Answers
Answer: 33 shares
Step-by-step explanation:
Amount invested in the company = $41.25
Price per share = $1 1/4 = $1.25
To calculate the amount of shares that Martha invested in the company will be:
= Amount invested in the company/Price per share
= $41.25/$1.25
= 33 shares
Martha invested 33 shares in the company.
Please answer this in two minutes
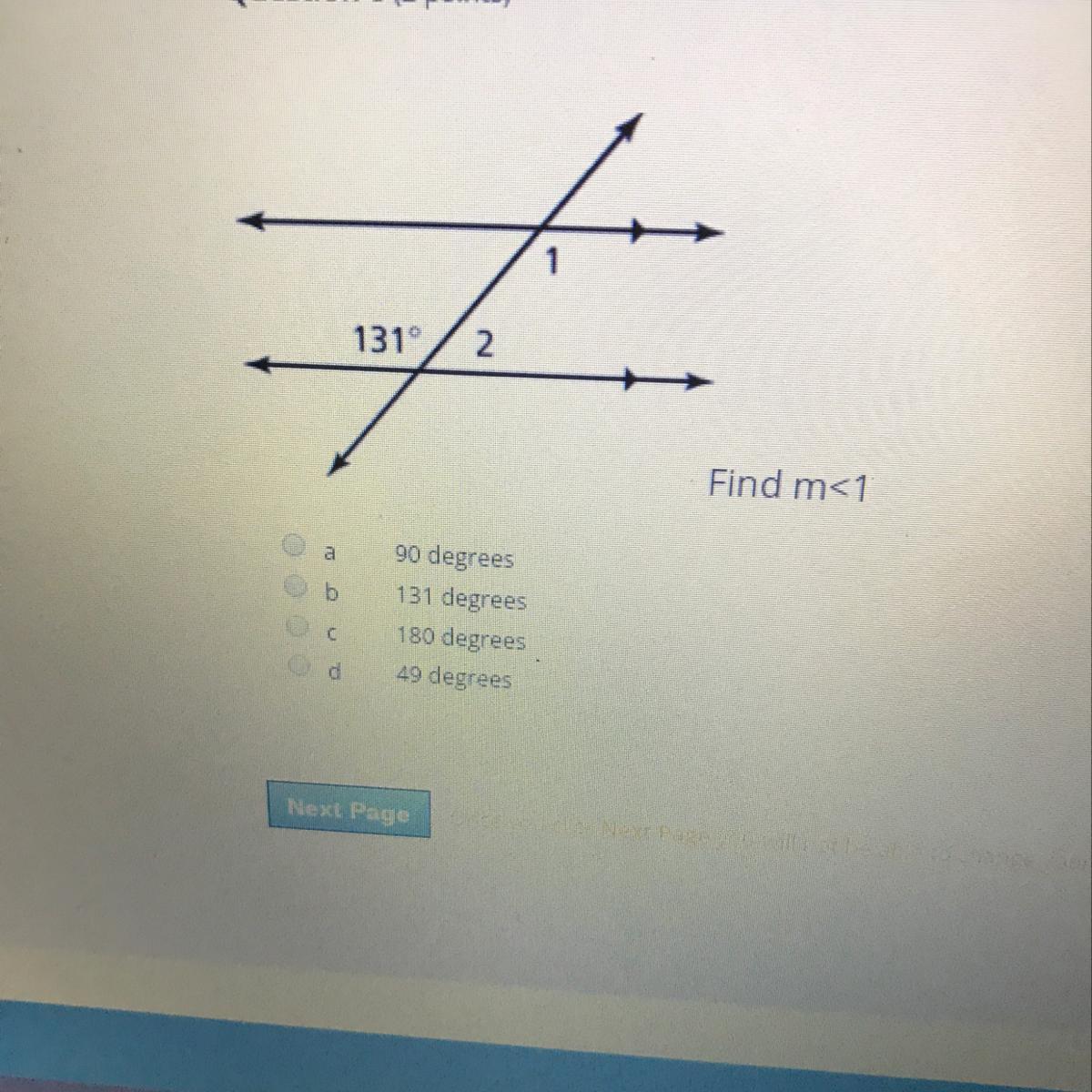
Answers
Answer:
131°.
Step-by-step explanation:
its equal to that other angle i forgot how but i learned this 1 week ago
the height of chance's beanstalk decreases by 50% per day when he stops feeding it. chance's beanstalk is 20 inches tall when he stops feeding it.
Answers
When Chance stops feeding the beanstalk, it loses half its height every day. Chance's beanstalk grows to a height of 20 inches after he stops feeding it= 20.5^t
What is unitary method?Area is the entire amount of space occupied by a flat (2-D) surface or an object's shape.
On a sheet of paper, draw a square using a pencil. It has two dimensions. The area of a shape on paper is the area that it occupies.
Consider your square as being composed of smaller unit squares.
The number of unit squares necessary to completely cover the surface area of a specific 2-D shape is used to calculate the area of a figure. Some typical units for measuring area are square cms, square feet, square inches, square meters, etc.
Draw unit squares with 1-centimeter sides in order to calculate the area of the square figures shown below. The shape will therefore be measured.
Hence, When Chance stops feeding the beanstalk, it loses half its height every day. Chance's beanstalk grows to a height of 20 inches after he stops feeding it= 20.5^t
learn more about unitary method click here:
brainly.com/question/24587372
#SPJ4
What is the slope of the line represented by the equation Y equals 4/5X -3?
-3
-4/5
4/5
3
Answers
Answer:
We conclude that the slope of the line represented by the equation \(y\:=\:\frac{4}{5}x-3\) would be:
m = 4/5Step-by-step explanation:
We know that the slope-intercept of the line equation is
\(y=mx+b\)
here
m is the slopeb is the y-interceptGiven the equation
\(y\:=\:\frac{4}{5}x-3\)
comparing with the slope-intercept of the line equation
The slope = m = 4/5
Thus, we conclude that the slope of the line represented by the equation \(y\:=\:\frac{4}{5}x-3\) would be:
m = 4/5dodie wants to plant roses in her triangular plot. there will be 1 plant at a corner. starting from that corner, each row will have 5 more plants than the row before it. she has 160 rose plants and wants the plot to have as many rows as possible. how many rows will dodie's plot have
Answers
Dodie's triangular plot with 160 rose plants will have 12 rows.
To solve it,
Assigning a variable to the number of rows we want to find. Assume that this variable is "n".
Since there are 5 more plants in each row than in the previous row,
We can use an arithmetic sequence to represent the number of plants in each row.
Specifically, the first row will have 1 plant, and the second row will have
1 + 5 = 6 plants, the third row will have 1 + 5 + 5 = 11 plants, and so on.
The formula for an arithmetic sequence is,
an = a1 + (n-1)d
Where an is the nth term of the sequence,
a1 is the first term,
And d is a common difference.
Using this formula, we can write an expression for the total number of plants in all n rows,
160 = n/2 (2 + (n-1)5)
Simplifying this equation, we get,
160 = 2.5n² + 2.5n - 5
Now we can solve for n using the quadratic formula,
n = (-2.5 ± √(2.5²+ 4(2.5)(165)))/(2(2.5))
After simplifying this equation, we get two solutions,
n = -13.2 and n = 12.2.
Since we can't have a negative number of rows, we'll take the positive solution, n = 12.2.
Now, since we can't have a fraction of a row, we'll round down to the nearest integer.
Therefore, Dodie's plot will have 12 rows.
To learn more about quadratic equations visit:
https://brainly.com/question/30098550
#SPJ12
steps for 540 + 6x = 810
Answers
Answer:
x = 45
Step-by-step explanation:
\(540 + 6x = 810\)
Step 1 : Collect like terms
\(6x = 810 - 540\)
Step 2 : Simplify
\(6x = 270\)
Divide both sides of the equation by 6
\( \frac{6x}{6} = \frac{270}{6} \)
Step 4 : Simplify
\(x = 45\)
I hope it helps :)
Answer:
Well...X=45
Step-by-step explanation:
Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation:540+6*x-(810)=0
Pull out like factors :-270 + 6x = 6 • (x - 45)
Solve : x-45 = 0::
Add 45 to both sides of the equation: x = 45