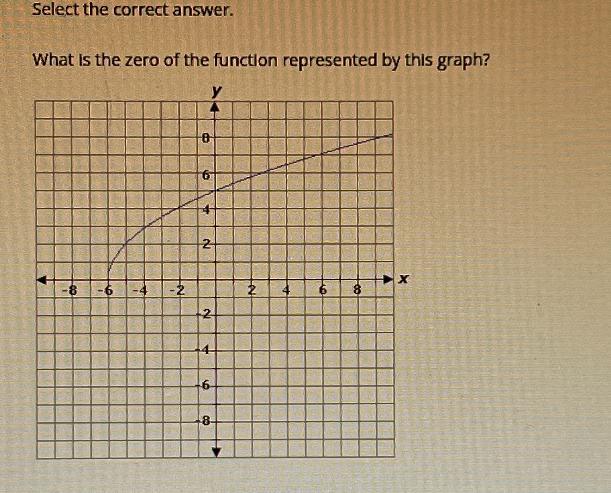
Select the correct answer.What is the zero of the function represents by this graph?SHORT QUICK ANSWERS ONLY NOT A TEST

Answer:

The equation of the polynomial in vertex form is \(y +8= (-2)\cdot (x-3)^{2}\), its vertex is \((h,k) = (3, -8)\).

The expression of the axis of symmetry is \(x = 3\).

The y-intercept of the function is -26.

Step-by-step explanation:

The vertex form of the second order polynomial is defined by the following expression:

\(y-k = C\cdot (x-h)^{2}\)  (1)

Where:

\(x\) - Independent variable, dimensionless.

\(y\) - Dependent variable, dimensionless.

\(h,k\) - Coordinates of the vertex, dimensionless.

\(C\) - Vertex constant, dimensionless.

Let \(y = -2\cdot x^{2}+12\cdot x - 26\), then we proceed to present the produre for the determination of the vertex form:

1) \(y = -2\cdot x^{2}+12\cdot x - 26\) Given

2) \(y = (-1)\cdot (2\cdot x^{2})+(-1)\cdot (-12\cdot x) + (-1)\cdot (26)\) \((-a)\cdot (-b) = a\cdot b\)/\((-a)\cdot b = -a\cdot b\)

3) \(y = (-1)\cdot (2\cdot x^{2}-12\cdot x +26)\) Distributive property

4) \(y = [(-1)\cdot (2)]\cdot (x^{2}-6\cdot x +13)\) Associative and distributive properties

5) \(y = (-2)\cdot [(x^{2}-6\cdot x+9)+4]\) \((-a)\cdot b = -a\cdot b\)

6) \(y = (-2) \cdot [(x-3)^{2}+4]\) Perfect square trinomial

7) \(y = (-2)\cdot (x-3)^{2}+4\cdot (-2)\) Distributive property

8) \(y = (-2)\cdot (x-3)^{2}+(-8)\) \((-a)\cdot b = -a\cdot b\)

9) \(y +8= (-2)\cdot (x-3)^{2}\) Compatibility of addition/Existence of the additive inverse/Modulative property/Result.

The equation of the polynomial in vertex form is \(y +8= (-2)\cdot (x-3)^{2}\), its vertex is \((h,k) = (3, -8)\).

The axis of symmetry is a line perpendicular to axis in which the square component of the vertex form is set. The expression of the axis of symmetry is \(x = 3\).

The y-intercept is the value of the polynomial when \(x = 0\), then, the value is:

\(y = -2\cdot (0)^{2}+12\cdot (0) -26\)

\(y = -26\)

The y-intercept of the function is -26.

Raw materials purchases in July - Payment for raw materials purchases in July = Desired ending raw materials inventory for July

X pounds - 0.35 * X pounds = 9,500 pounds

Solving this equation will give us the value of X, which represents the pounds of raw materials that should be purchased in July.

To determine the number of pounds of raw materials that should be purchased in July, we need to calculate the raw materials production needs for August and then consider the inventory policies given in the information provided.

Each unit of finished goods requires 5 pounds of raw materials. The budgeted unit sales for August are 19,000 units. Therefore, the raw materials production needs for August would be 19,000 units multiplied by 5 pounds per unit, which equals 95,000 pounds.

The ending raw materials inventory equals 10% of the following month’s raw materials production needs. Therefore, the desired ending raw materials inventory for July would be 10% of 95,000 pounds, which is 9,500 pounds.

To calculate the raw materials purchases for July, we need to consider the payment terms provided. Thirty-five percent of raw materials purchases are paid for in the month of purchase and 65% in the following month.

Let's assume the raw materials purchases for July are X pounds. Then the payment for 35% of X pounds will be made in July, and the payment for 65% of X pounds will be made in August.

The payment for raw materials purchases in July (35% of X pounds) will be:

0.35 * X pounds

The payment for raw materials purchases in August (65% of X pounds) will be:

0.65 * X pounds

Since the raw materials purchases for July should cover the desired ending raw materials inventory for July (9,500 pounds), we can set up the following equation:

Raw materials purchases in July - Payment for raw materials purchases in July = Desired ending raw materials inventory for July

X pounds - 0.35 * X pounds = 9,500 pounds

Solving this equation will give us the value of X, which represents the pounds of raw materials that should be purchased in July.

for such more question on equation

#SPJ8

Answer:

z = 12

Step-by-step explanation:

Solve for  z  by simplifying both sides of the equation, then isolating the variable.

The number of gallons of water that you drink in a year is 240.9 gallons.

We have to find the number of gallons of water that you drink in a year.

For that, first wee need to find the amount of water that you drink in a day.

Each person will drink water in a day in different amounts.

We can take an average of 2.5 liters that a man drink in a day.

Then

Amount of water drink in a year = 2.5 × 365

                                                      = 912.5 liters

Now we need to find the amount of water in gallons.

Convert liters in gallons.

1 liter = 0.264 gallons

So,

912.5 liters = 912.5 × 0.264 gallons

                  = 240.9 gallons

Hence the amount is 240.9 gallons.

Learn more about Conversion here :

https://brainly.com/question/31419854

#SPJ1

Finding the line of best fit is something a Machine Learning Model would do.

This particular ML model is called "Linear Regressor" or "Linear Regression Model". Look it up and there are definitely calculators for it, as it is relatively simple.

You can also, if you know how to use ML libraries and code, use Python to determine the value of \(b\).

Hope this helps.

A = \(\frac{1}{2}h(b_{1} +b_{2} )\)

If A = 136 when \(b_{1}\) = 7 and h = 16, find \(b_{2}\)

We are given the equation that we are working with:

A = \(\frac{1}{2}h(b_{1} +b_{2} )\)

We are given certain values that the variables, in this case, are equal to:

A = 136

\(b_{1}\) = 7

h = 16

Substitute the given variables in the given equation for the corresponding numbers:

A = \(\frac{1}{2}h(b_{1} +b_{2} )\)

136 = \(\frac{1}{2}\) * 16 (7 + \(b_{2}\))

We know all the values in the equation except  \(b_{2}\). In order to find  \(b_{2}\) we must isolate it on one side of the equation

136 = 8 (7 + \(b_{2}\))

\(\frac{136}{8}\) = \(\frac{8 (7 + b_{2}) }{8}\)

17 = 7 + \(b_{2}\)

17 - 7 = 7 - 7 + \(b_{2}\)

10 =   \(b_{2}\)

If   \(b_{2}\) is equal to 10 then if we plug it back into the given equation both sides of the equation should equal each other. Remember to use PEMDAS

136 = \(\frac{1}{2}\) * 16 (7 + \(b_{2}\))

136 = \(\frac{1}{2}\) * 16 (7 + 10)

136 = \(\frac{1}{2}\) * 16 (17)

136 = 8 (17)

136 = 136

\(b_{2}\) = 10

22>x>36 is the range for the third side's measurement when two sides of a triangle are measured at 7 km and 29 km.

Given that,

When the other two sides of a triangle are measured at 7 km and 29 km.

We have to determine the range for the third side's measurement.

We know that,

Take the measured sides.

7 km and 29 km

So, we can write as

The two sides added together are greater than the third side.

So, take one side as x

We get,

7+x>29

Taking 7 to the right side we get negative 7
x>29-7

x>22

Now taking 29 to left side and x to sides

7+29>x

36>x

Therefore, 22>x>36 is the range for the third side's measurement when two sides of a triangle are measured at 7 km and 29 km.

To learn more about range visit: https://brainly.com/question/28135761

#SPJ4

Answer:

m<wzx = 71

Step-by-step explanation:

Assuming these are interior angles of a triangle.

The sum of all three interior angles of a triangle is always 180 degrees, therefore:

m<xyz + m<wxz + m<wzx = 180

Substitute our values:

58 + 51 + m<wzx = 180

m<wzx = 180 - 58 - 51

m<wzx = 71

The volume of the cone is 13 cm³. option D

To determine the volume of the cone, we have that;

The formula for calculating the volume of a cone is expressed as;

Volume = (1/3)πr ²√(L ² - r ²).

Such that;

Substitute the values, we have;

Volume = 1/3 × 3.14 ² × √(25 - 9)

Find the squares, we get;

Volume, V = 1/3 × 9. 86 × √16

Find the square root

Volume, V = 1/3 × 9.86 × 4

Volume, V = 13 cm³

Learn more about volume at:
#SPJ1

9. The value of x is 7

10. In the figure  x = 10

11. The relationship is that their sum is 180 degrees

This relationship is known as the Same-Side Interior Angles Theorem.

12. The statement is true.

Supporting statement: If the two lines are parallel, then the alternate exterior angles created by the transversal line are equal

14 < 3 = 94 degrees

9. The value of x is solved using the knowledge of corresponding angles are equal

< A = < B

4x = 3x + 7

x = 7

10. In the figure < 3 and < 6 are alternate internal angles which is equal

7x - 10 = 5x + 10

7x - 5x = 10 + 10

2x = 20

x = 10

11. The relationship between the interior angles on the same side is that their sum is 180 degrees

This relationship is known as the Same-Side Interior Angles Theorem. It is a fundamental concept in geometry and is used to solve problems involving parallel lines and transversals.

12. The statement is true.

Supporting statement: If the two lines are parallel, then the alternate exterior angles created by the transversal line are equal

13. The measure of w is solved using the idea of vertical angels

w + 85 = 148

w = 148 - 85

w = 63

14. The mistake is that < 5 is not corresponding angle to < 2

The correct solution is < 3 = < 5 alternate internal angles

< 3 + 86 = 180 supplementary angles

< 3 = 180 - 86

< 3 = 94 degrees

Learn more about corresponding angle at:

https://brainly.com/question/28769265

#SPJ2

Answer:

what are the other decimals?

Step-by-step explanation:

Given:

To find the degree of the polynomial:

The degree of the given polynomial is, 2+3=5

So, the given polynomial is a fifth-degree polynomial.

Thus, the answer is a fifth-degree polynomial.

The correct answer is option D: A line passes through the point (0, 0) and continues through the point (12, 3)

For the first question:

The table shows a proportional relationship between x and y. To describe what the graph of this proportional relationship would look like, we can examine the given data points.

The data points are (12, 3), (8, 26), and (24, ?). We can observe that as x increases, y also increases. This indicates a positive correlation between the variables. Additionally, we can see that the ratio of y to x remains constant for each data point.

Now, let's analyze the answer options:

A. A line passes through the point (0, 0) and continues through the point (3, 12).

This answer option does not align with the given data because there is no data point with an x-value of 3 and a corresponding y-value of 12.

B. A line passes through the point (0, 0) and continues through the point (2, 8).

This answer option aligns with the given data because (2, 8) is a valid data point from the table, and the line passes through the origin (0, 0).

C. A line passes through the point (0, 0) and continues through the point (6, 24).

This answer option does not align with the given data because there is no data point with an x-value of 6 and a corresponding y-value of 24.

D. A line passes through the point (0, 0) and continues through the point (12, 3).

This answer option aligns with the given data because (12, 3) is a valid data point from the table, and the line passes through the origin (0, 0).

Based on the analysis, the correct answer is option D: A line passes through the point (0, 0) and continues through the point (12, 3). This accurately represents the graph of the proportional relationship given in the table.

For the second question, I'm sorry, but you didn't provide the multiple-choice options or the complete question. Could you please provide the question and options so that I can assist you further?

for more such question on point visit

https://brainly.com/question/1859113

#SPJ8

Answer:

I think is 15 dollars.

Step-by-step explanation:

each pound cost 1.5 multiply it by 10

Answer:

$15

Step-by-step explanation:

4 pounds are $6

10pounds are $?

1 pound would be $1.5, because 6/4 = 3/2= 1.5

If one pound is 1.5 dollars, 10 pounds would be 10*1.5=$15

If Gavin contributes towards a Pension fund (7,5% of his Basic Salary), then his net salary will be reduced by the amount he contributed towards pension fund i.e. R652.5.

1.1 Name of employee is Gavin Pillay. 1.2 UIF stands for Unemployment Insurance Fund. UIF is a benefit to provide short-term relief to workers who lose their jobs, or can't work due to illness, maternity or adoption leave. 1.3 The UIF paid by Gavin is calculated correctly.

Firstly, we need to calculate Gross Salary of Gavin, which is given as: Basic Salary + Overtime + M = R8700 + R1200 + R3201 = R13101Then, calculate total deductions from gross salary.

Total Deductions = PAYE + UIF = R1200 + 87 = R1287Hence, Gavin's net salary = Gross salary - Total Deductions = R13101 - R1287 = R11814Therefore, UIF paid by Gavin is calculated correctly as R87.1.4 This payslip is for the month of May i.e.

31/05/2023.1.5 Basic salary of Gavin = R8700. Deduct 7.5% of his basic salary to calculate his pension fund contribution. Pension Fund Contribution = 7.5/100 x R8700 = R652.5.1.6

Total deductions of Gavin includes PAYE, UIF and pension fund contribution.

Therefore, Total Deductions = PAYE + UIF + Pension Fund Contribution = R1200 + R87 + R652.5 = R1939.5.1.7

Gavin's age can not be determined as his date of birth is not provided.1.8 Address of Gavin's workplace is 21 Halsted Road, Pietermaritzburg?

To learn more about : pension fund

https://brainly.com/question/31531270

#SPJ8

Answer:

see below

Step-by-step explanation:

6/8 of 8 equal parts = 6

3/4 of 4 equal parts  = 3

Since the leading coefficient of P(x) is 1, and has roots of multiplicity 2 at x=1 and x=0, and a root of multiplicity 1 at x=-3 we get that:

Simplifying the above polynomial we get:

Answer: A formula for P(x) is:

The probability distribution of the number of customers that enter the store on a given day is described as follows:

Poisson with a mean of 70 customers.

In a Poisson distribution, the mass function probability that X represents the number of successes of a random variable is given by the equation presented as follows:

\(P(X = x) = \frac{e^{-\mu}\mu^{x}}{(x)!}\)

The parameters are:

A combination of Poisson variables is a Poisson variable, hence the daily distribution is a Poisson variable with mean given by the sum of these following observations:

Hence the mean is of:

8 + 16 + 18 + 28 = 70 customers.

More can be learned about the Poisson distribution at https://brainly.com/question/7879375

#SPJ1

The function f(x) = -2(4)ˣ⁺¹ +140 represents the number of tokens a child has x hours after arriving at an arcade. The practical domain and range of the function are x ≥ 0 and The practical range of the situation is [140, ∞).

The given function is f(x) = -2(4)ˣ⁺¹+ 140, which represents the number of tokens a child has x hours after arriving at an arcade.

To determine the practical domain and range of the function, we need to consider the constraints and limitations of the situation.

For the practical domain, we need to identify the valid values for x, which in this case represents the number of hours the child has been at the arcade. Since time cannot be negative in this context, the practical domain is x ≥ 0, meaning x is a non-negative number or zero.

Therefore, the practical domain of the situation is x ≥ 0.

For the practical range, we need to determine the possible values for the number of tokens the child can have. Looking at the given function, we can see that the term -2(4)ˣ⁺¹represents a decreasing exponential function as x increases. The constant term +140 is added to shift the graph upward.

Since the exponential term decreases as x increases, the function will have a maximum value at x = 0 and approach negative infinity as x approaches infinity. However, due to the presence of the +140 term, the actual range will be shifted upward by 140 units.

Therefore, the practical range of the situation will be all real numbers greater than or equal to 140. In interval notation, we can express it as [140, ∞).

To summarize:

- The practical domain of the situation is x ≥ 0.

- The practical range of the situation is [140, ∞).

Know more about the domain here:
https://brainly.com/question/30096754

#SPJ8

To convert miles per hour to meters per second divide by 2.237

128 miles per hour / 2.237 = 57.22 meters per second.

Using the first equation:

57.22 = sqrt(2 x 9.81 x h)

Remove the sqrt by raising both sides to the second power:

57.22^2 = (2 x 9.81 x h)

Simplify Both sides:

3274.1284 = 19.62h

Divide both sides by 19.62:

H = 3274.1284/ 19.62

H = 166.88 meters

Answer:

17.32 meters

Step-by-step explanation:

Let’s call the height of the tower H. The distance from the point to the base of the tower is 10 m. The angle of elevation from the point to the top of the tower is 60 degrees.

Using trigonometry, we can calculate that:

tan (60) = H / 10

H = 10 * tan (60)

H = 10 * √3

H = 17.32 m

Therefore, the height of the tower is 17.32 meters.

Let me know if I helped :)

Answer:To find the lateral area and surface area of a cone with a diameter of 3.4 centimeters and a slant height of 6.5 centimeters, we first need to find the radius of the cone. The radius is half of the diameter, so it is 1.7 centimeters.

The lateral area of a cone is given by the formula LA = πrs, where r is the radius and s is the slant height. Plugging in the values we have, we get LA = π(1.7)(6.5) = 35.042 square centimeters.

The surface area of a cone is given by the formula SA = πr^2 + πrs, where r is the radius and s is the slant height. Plugging in the values we have, we get SA = π(1.7)^2 + π(1.7)(6.5) = 47.097 square centimeters.

Therefore, the lateral area of the cone is approximately 35.042 square centimeters and the surface area of the cone is approximately 47.097 square centimeters.

I hope this helps!

Step-by-step explanation:

Step-by-step explanation:

Doesn't have solution...

- Real and rational number.

It's a rational number because it can be represented by the integer of integer numbers. It's also a real number because rational numbers belong to the real set of numbers and the number doesn't contain an imaginary component (i).

It's not a natural or whole number because it can't be used to count or order things.

It's not an integer because it can't eb written without using a fractional component.

well, since we know that there are 180° in π radians, how many degrees will it be in 345°?

\(\begin{array}{ccll} degrees&radians\\ \cline{1-2} 180&\pi \\ 345&x \end{array}\implies \cfrac{180}{345}~~ = ~~\cfrac{\pi }{x}\implies \cfrac{12}{23}~~ = ~~\cfrac{\pi }{x} \\\\\\ 12x=23\pi \implies x=\cfrac{23\pi }{12}\)

The number of tens between the given numbers are 1883.

The number of tens between two numbers can be calculated by the concept of proportions. A proportion is a fraction of a total amount, and the measures are related using a rule of three. Due to this, relations between variables, either direct or inverse proportional, can be built to find the desired measures in the problem. Now, to find the number of tens we divide the number by 10. So, the number of tens in the given numbers are

9312/10 = 931 (approximately)

9522/10 = 952 (approximately).

Now, the numbers of tens between the two given numbers can be calculated by adding the number of tens in them that is,

952 + 931 = 1883 tens between the two numbers.

Learn more about Proportion at:

brainly.com/question/28279454

#SPJ1

Answer:

B and D

Step-by-step explanation:

Both B and D cross over the point (4, 8) therefore they share the solution (4, 8)