Seamus has a truck of chairs and tables for a party. There are 8 times as many chairs as tables, for a total of 56 chairs in the truck. How many tables are in the truck?
Answers
Answer:
7
Step-by-step explanation:
Related Questions
A transponder for a toll bridge costs $17.50. With the transponder, the toll is $5 each time you cross the bridge. The only other option is toll-by-plate, for which the toll is $7.25 each time you cross the bridge with an additional administrative fee of $1.25 for each crossing. How many times would you need to cross the bridge for the costs of the two toll options to be the same?
Answers
Answer: you would need to cross the bridge 5 times
Step-by-step explanation:
costing a total of $42.50 for each option.
hope this helps
A market research firm supplies manufacturers with estimates of the retail sales of their products from samples of retail stores. Marketing managers are prone to look at the estimate and ignore sampling error. A random sample of 36
stores this year shows mean sales of 78
units of a small appliance with a standard deviation of 13
units. During the same point in time last year, a random sample of 49
stores had mean sales of 90
units with standard deviation 16
units.
It is of interest to construct a 95 percent confidence interval for the difference in population means 1−2
, where 1
is the mean of this year's sales and 2
is the mean of last year's sales.
Answers
As a result, we can claim with 95% certainty that the population linear difference means 1-2 is between -21.48 and -2.52 units of small appliances.
What is a linear equation?In algebra, a linear equation has the form y=mx+b. The slope is denoted by B, while the y-intercept is denoted by m. Because y and x are variables, the preceding sentence is sometimes referred to as a "linear equation with two variables." Bivariate linear equations are two-variable linear equations. Linear equations may be found in various places: 2x - 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, and 3x - y + z = 3. When an equation has the form y=mx+b, where m represents the slope and b represents the y-intercept, it is said to be linear. A linear equation is one that contains the formula y=mx+b, with m signifying the slope and b denoting the y-intercept.
We may use the following calculation to get a 95% confidence range for the difference in population means 1-2:
\((x1 - x2) t(\alpha/2, df) * \sqrt(s12/n1 + s22/n2)\)
where:
Initially, we must compute the degrees of freedom:
\(df = ((s12/n1) + s22/n2)2/((s12/n1) + (s22/n2)2/(n2-1))\\df = ((13^2/36 + 16^2/49)^2) / ((13^2/36)^2/35 + (16^2/49)^2/48) = 67.94\\(78 - 90) 2.00 * \sqrt(132/36 + 162/49)\\CI = -12 +2.00 * 4.742\\CI = -12+ 9.484\\CI = (-21.48, -2.52) (-21.48, -2.52)\)
As a result, we can claim with 95% certainty that the population difference means 1-2 is between -21.48 and -2.52 units of small appliances.
To know more about linear equation visit:
https://brainly.com/question/11897796
#SPJ1
Homework part2 need help asap

Answers
The key features of the given quadratic functions are listed below.
What is the graph of a quadratic function?In Mathematics and Geometry, the graph of any quadratic function would always form a parabolic curve because it is a u-shaped. Based on the first quadratic function, we can logically deduce that the graph is an upward parabola because the coefficient of x² is positive and the value of "a" is greater than zero (0) i.e 3 > 0.
For the quadratic function y = 3x² - 5, the key features are as follows;
Axis of symmetry: x = 0.
Vertex: (0, -5).
Domain: [-∞, ∞]
Range: [-5, ∞]
For the quadratic function y = -2x² + 12x - 15, the key features are as follows;
Axis of symmetry: x = 3.
Vertex: (3, 3).
Domain: [-∞, ∞]
Range: [-∞, 3]
For the quadratic function y = -x² + 1, the key features are as follows;
Axis of symmetry: x = 0.
Vertex: (0, 1).
Domain: [-∞, ∞]
Range: [-∞, 1]
For the quadratic function y = 2x² - 16x + 30, the key features are as follows;
Axis of symmetry: x = 4.
Vertex: (4, -2).
Domain: [-∞, ∞]
Range: [-2, ∞]
Read more on quadratic functions here: brainly.com/question/24020644
#SPJ1

Here are a few pairs of positive numbers whose sum is 34. (3 pts)
a. Find the product of each pair of numbers.
First
Number
1
4
8
14
Second
Number
33
30
26
20
b. Which pair of numbers that have a sum of 34 will produce the largest possible
product? What is that product?
Answers
Answer: 280
Step-by-step explanation:
The products of each pair of numbers are:
1 x 33 = 33
4 x 30 = 120
8 x 26 = 208
14 x 20 = 280
b. To find the pair of numbers that will produce the largest possible product, we need to look for the pair with the closest product to 340 (the square of 17, which is the average of the two numbers).
The pair of numbers with the closest product to 340 is 14 and 20, whose product is 280. Therefore, the pair of numbers that will produce the largest possible product is 14 and 20, and the product is 280.
Non Shaded Shaded
Area
Area
8
Find the radius
of the small circle

Answers
Answer:
The answer is 16pi or 50.3cm² to 1 d.p
Step-by-step explanation:
The non shaded=area of shaded
d=8
r=d/2=4
A=pir³
A=p1×4²
A=pi×16
A=16picm² or 50.3cm² to 1d.p
Answer:
3.45 cm (3 s.f.)
Step-by-step explanation:
We have been given a 5-sided regular polygon inside a circumcircle. A circumcircle is a circle that passes through all the vertices of a given polygon. Therefore, the radius of the circumcircle is also the radius of the polygon.
To find the radius of a regular polygon given its side length, we can use this formula:
\(\boxed{\begin{minipage}{6 cm}\underline{Radius of a regular polygon}\\\\$r=\dfrac{s}{2\sin\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
Substitute the given side length, s = 8 cm, and the number of sides of the polygon, n = 5, into the radius formula to find an expression for the radius of the polygon (and circumcircle):
\(\begin{aligned}\implies r&=\dfrac{8}{2\sin\left(\dfrac{180^{\circ}}{5}\right)}\\\\ &=\dfrac{4}{\sin\left(36^{\circ}\right)}\\\\ \end{aligned}\)
The formulas for the area of a regular polygon and the area of a circle given their radii are:
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{nr^2\sin\left(\dfrac{360^{\circ}}{n}\right)}{2}$\\\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}\)
\(\boxed{\begin{minipage}{6 cm}\underline{Area of a circle}\\\\$A=\pi r^2$\\\\where:\\\phantom{ww}$\bullet$ $A$ is the area.\\\phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
Therefore, the area of the regular pentagon is:
\(\begin{aligned}\textsf{Area of polygon}&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(\dfrac{360^{\circ}}{5}\right)}{2}\\\\&=\dfrac{5 \cdot \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\sin\left(72^{\circ}\right)}{2}\\\\&=\dfrac{\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}}{2}\\\\&=\dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}\\\\&=110.110553...\; \sf cm^2\end{aligned}\)
The area of the circumcircle is:
\(\begin{aligned}\textsf{Area of circumcircle}&=\pi \left(\dfrac{4}{\sin\left(36^{\circ}\right)}\right)^2\\\\&=\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\&=145.489779...\; \sf cm^2\end{aligned}\)
The area of the shaded area is the area of the circumcircle less the area of the regular pentagon plus the area of the small central circle.
The area of the unshaded area is the area of the regular pentagon less the area of the small central circle.
Given the shaded area is equal to the unshaded area:
\(\begin{aligned}\textsf{Shaded area}&=\textsf{Unshaded area}\\\\\sf Area_{circumcircle}-Area_{polygon}+Area_{circle}&=\sf Area_{polygon}-Area_{circle}\\\\\sf 2\cdot Area_{circle}&=\sf 2\cdot Area_{polygon}-Area_{circumcircle}\\\\2\pi r^2&=2 \cdot \dfrac{40\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)}{\sin^2\left(36^{\circ}\right)}-\dfrac{16\pi}{\sin^2\left(36^{\circ}\right)}\\\\\end{aligned}\)
\(\begin{aligned}2\pi r^2&=\dfrac{80\sin\left(72^{\circ}\right)-16\pi}{\sin^2\left(36^{\circ}\right)}\\\\r^2&=\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}\\\\r&=\sqrt{\dfrac{40\sin\left(72^{\circ}\right)-8\pi}{\pi \sin^2\left(36^{\circ}\right)}}\\\\r&=3.44874763...\sf cm\end{aligned}\)
Therefore, the radius of the small circle is 3.45 cm (3 s.f.).

I am stumped >:( ahhhhhhh

Answers
Answer:
\(\frac{1}{32} yards^{3}\)
Step-by-step explanation:
\(V=w*h*l\)
↓
\(V= \frac{1}{4} *\frac{1}{4} *\frac{1}{2}\)
=
\(\frac{1}{32} yards^{3}\\\)
Hope this helps!
What is the translation from
a) shape X to shape Z?
b) shape Z to shape X?

Answers
The translation form of each shape is given as follows:
a) X to Z: (x, y) -> (x + 5, y + 2).
b) Z to X: (x, y) -> (x - 5, y - 2).
What are the translation rules?The four translation rules are defined as follows:
Left a units: x -> x - a.Right a units: x -> x + a.Up a units: y -> y + a.Down a units: y -> y - a.For the composition of translations, we add the coordinates, hence:
-2 + 7 = 5.5 - 3 = 2.Hence the rule from X to Z is given as follows:
(x, y) -> (x + 5, y + 2).
From Z to X, we have the inverse rule, hence:
(x, y) -> (x - 5, y - 2).
More can be learned about translation at brainly.com/question/29209050
#SPJ1
Which polynomial is prime?
O 3x³ + 3x² - 2x - 2
O 3x³ − 2x² + 3x − 4
-
O
4x³ + 2x² + 6x + 3
O
4x³+4x²-3x - 3

Answers
Answer:
B
Step-by-step explanation:
a prime polynomial is one which does not factor into 2 binomials.
its only factors are 1 and itself
attempt to factorise the given polynomials
3x³ + 3x² - 2x - 2 ( factor the first/second and third/fourth terms )
= 3x²(x + 1) - 2(x + 1) ← factor out common factor (x + 1) from each term
= (x + 1)(3x² - 2) ← in factored form
--------------------------------------------------
3x³ - 2x² + 3x - 4 ( factor the first/second terms
= x²(3x - 2) + 3x - 4 ← 3x - 4 cannot be factored
thus this polynomial is prime
----------------------------------------------------
4x³ + 2x² + 6x + 3 ( factor first/second and third/fourth terms )
= 2x²(2x + 1) + 3(2x + 1) ← factor out common factor (2x + 1) from each term
= (2x + 1)(2x² + 3) ← in factored form
-------------------------------------------------
4x³ + 4x² - 3x - 3 ( factor first/second and third/fourth terms )
= 4x²(x + 1) - 3(x + 1) ← factor out common factor (x + 1) from each term
= (x + 1)(4x² - 3) ← in factored form
--------------------------------------------------
the only polynomial which does not factorise is
3x³ - 2x² + 3x - 4
What is the volume of the solid figure (with congruent, parallel bases) that has a height of 11 feet and the base shown?
volume =
ft 3

Answers
The calculated volume of the solid figure is 421.08 cubic feet
How to determine the volume of the solid figureFrom the question, we have the following parameters that can be used in our computation:
Base area = 38.28 square feet
Height = 11 feet
Using the above as a guide, we have the following:
Volume = Base area * Height
substitute the known values in the above equation, so, we have the following representation
Volume = 38.28 * 11
Evaluate
Volume = 421.08
Hence, the volume of the solid figure is 421.08 cubic feet
Read more about volume at
https://brainly.com/question/463363
#SPJ1
Calculate the side lengths a and b to two decimal places

Answers
Answer:
E
Step-by-step explanation:
using the Sine rule in Δ ABC
\(\frac{a}{sinA}\) = \(\frac{b}{sinB}\) = \(\frac{c}{sinC}\)
where a is the side opposite ∠ A , b opposite ∠ B , c opposite ∠ C
we require to calculate ∠ C
∠ C = 180° - (64 + 85)° = 180° - 149° = 31°
then to find a , using
\(\frac{a}{sinA}\) = \(\frac{c}{sinC}\)
\(\frac{a}{sin64}\) = \(\frac{9.3}{sin31}\) ( cross- multiply )
a × sin31° = 9.3 × sin64° ( divide both sides by sin31° )
a = \(\frac{9.3sin64}{sin31}\) ≈ 16.23 ( to 2 decimal places )
then to find b , using
\(\frac{b}{sinB}\) = \(\frac{c}{sinC}\)
\(\frac{b}{sin85}\) = \(\frac{9.3}{sin31}\) ( cross- multiply )
b × sin31° = 9.3 × sin85° ( divide both sides by sin31° )
b = \(\frac{9.3sin85}{sin31}\) ≈ 17.99 ( to 2 decimal places )
An auto dealer buys a truck at a cost of $15,800 and sells it to consumers at a price of $33,970. Find the amount of the markup, and the percent markup based on the selling price. Round to the nearest tenth percent.
Answers
Answer:
i dont know how to help you:(
What is the value of x in the figure? Enter your answer in the box.
145º
(2x + 15)
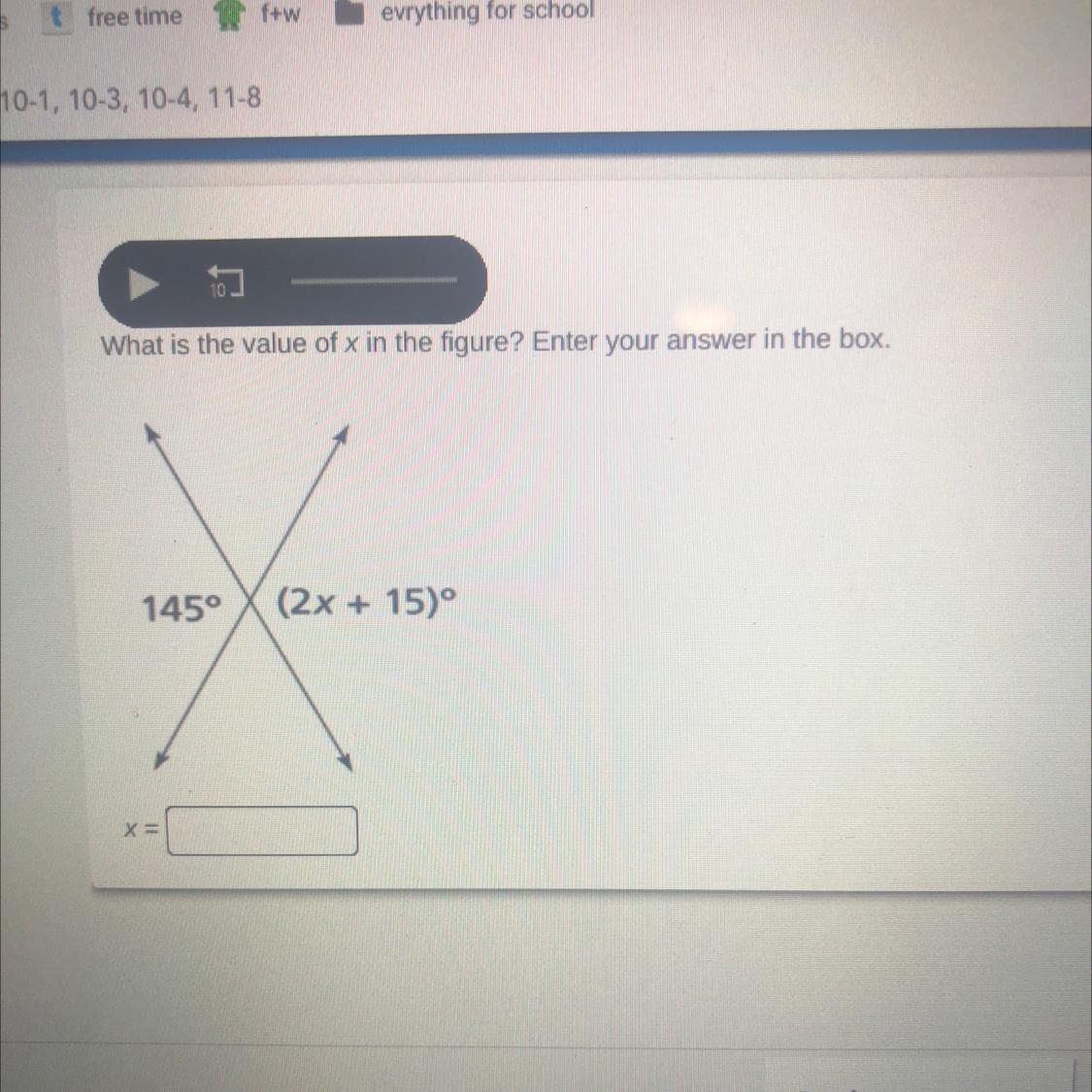
Answers
Answer:
x = 65
Step-by-step explanation:
The angle labeled with the expression " ( 2x + 15 ) " and the angle with the measure of 145° are vertical angles
Vertical angles are congruent (In other words, they are equal to each other)
Hence, 2x + 15 = 145
^ ( Note that we just created an equation that we can use
to solve for x )
Using that same equation we then solve for x
2x + 15 = 145
step 1 subtract 15 from each side
15 - 15 cancels out
145 - 15 = 130
we now have 130 = 2x
step 2 divide each side by 2
130 / 2 = 65
2x / 2 = x
we're left with x = 65
PLEASE HELP ASAP!!!
I'd really appreciate the help, thanks in advance.
The questions below can be solved using the relation between angular size, physical size and distance. For the questions below, provide a complete solution with explanation.
1. Find the Sun's diameter. The sun has an angular diameter of about 0.5° and an average distance from the Earth of about 150 million km. What is the sun's approximate physical diameter? Compare your answer to the actual value of 1 390 000 km.
2. Find a Star's Diameter. The supergiant star Betelgeuse (in the constellation Orion) has a measured angular diameter of 0.040 arcsecond from Earth and a distance from Earth of 720 light-years. What is the actual diameter of Betelgeuse? Compare your answer to the size of our Sun and the Earth-Sun distance.
Answers
The physical diameter of the sun will be 1309000km and the percentage of difference between the diameters will be 5.8%.
How to calculate the diameter?From the information, the sun has an angular diameter of about 0.5° and an average distance from the Earth of about 150 million km. The angular diameter in radians will be:
= 0.5π / 180
= 0.008727 radians
Distance from the sun = 150 × 10^6
The physical diameter of the sun will be:
= 150 × 10^6 × 0.008727
= 1309000km
The difference between the diameters will be:
= 1390000 - 1309000
= 8.1 × 10^4.
The percentage of difference will be:
= (8.1 * 10^4) / 1390000 × 100
= 5.8%
Learn more about sun on:
brainly.com/question/15837114
#SPJ1
Find 2 numbers if their difference is 16 and their ratio is 5:7
Answers
Answer:
40 and 56.
Step-by-step explanation:
x - y = 16 where x is the greater number
If the ratio is 5:7 one number must be 7/12 of the total of the 2 numbers, so:
x = 7/12(x + y)
From first equation x = y + 16, so substituting for x:-
y + 16 = 7/12( 2y + 16)
Multiplying through by 12:
12y + 192 = 7(2y + 16)
12y + 192 = 14y + 112
2y = 192 - 112 = 80
y = 40
So x = 40+ 16 = 56.
Answer:
The numbers are:
56 and 40
Step-by-step explanation:
a - b = 16 eq. 1
5a = 7b eq. 2
from eq. 1:
a = 16 + b
relacing this last eq. in eq. 2
5(16+b) = 7b
5*16 + 5*b = 7b
80 + 5b = 7b
80 = 7b - 5b
80 = 2b
80/2 = b
40 = b
From eq. 1
a - b = 16
a - 40 = 16
a = 16 + 40
a = 56
Check:
from eq. 2:
5a = 7b
5*56 = 7*40 = 280
WILL GIVE BRAINLIEST
Find the equation of the line
perpendicular to y=-2x + 1 that
also intersects the point (8, 2).
y- Hx+ 1
Enter
Answers
Answer:
y=1/2x-2
Step-by-step explanation:
perpendicular lines have a neg. reciprocal for the slope.
for example:
in this equation y=-2x+1
-2 is the slope and the negative reciprocal would be 1/2
hence, the slop of our new line is 1/2
y=1/2x+b
we can substitute the coordinates given for x and y:
2=1/2(8)+b
2=4+b
-2=b
hence the new equation is y=1/2x-2
which inequality is true if p=3.4
Answers
Answer:
F.3p < 10.2
G.13.6 ≤ 3.9p
H.5p > 17.1
J.8.5
Your friend printed a picture of a regular 18-gon. She wants to cut the 18-gon into right triangles. If she divides the figure into 36 right triangles, what are the measures of the non-right angles of each triangle?
Answers
The measures of the non-right angles of each triangle are 40 degrees and 50 degrees.
The sum of the interior angles of a regular 18-gon can be found using the formula:
S = (n - 2) × 180 degrees
n is the number of sides of the polygon.
Substituting n = 18 we get:
S = (18 - 2) × 180 degrees
= 2880 degrees
The 18-gon into 36 right triangles need to draw 18 lines from the center of the polygon to its vertices dividing the polygon into 36 congruent sectors each with a central angle of 360 degrees / 18 = 20 degrees.
Each sector is an isosceles triangle with two sides of equal length radiating from the center of the polygon.
The vertex angle of each isosceles triangle is equal to twice the central angle or 40 degrees.
Since the vertex angle of a right triangle is 90 degrees the two non-right angles of each right triangle are 40 degrees and 50 degrees.
For similar questions on non-right angles
https://brainly.com/question/30571649
#SPJ11
How do I do number 1??
Help me it’s due tomorrow!!!

Answers
The values of x and y are 20 and 12.
The values of x and y are -3 and 2.
We have,
In a parallelogram,
- Opposite sides are congruent:
The opposite sides of a parallelogram have equal lengths.
- Opposite angles are congruent:
The opposite angles of a parallelogram have equal
Now,
a)
Opposite angles are congruent:
So,
5x + 29 = 7x - 11
29 + 11 = 7x - 5x
40 = 2x
2x = 40
x = 40/2
x = 20
And,
3y + 15 = 5y - 9
15 + 9 = 5y - 3y
24 = 2y
y = 24/2
y = 12
b)
Opposite sides are congruent:
So,
-6x = -4x + 6
-6x + 4x = 6
-2x = 6
x = -3
And,
7y + 3 = 12y - 7
12y - 7y = 3 + 7
5y = 10
y = 2
Thus,
The values of x and y are 20 and 12.
The values of x and y are -3 and 2.
Learn more about parallelograms here:
https://brainly.com/question/1563728
#SPJ1
For the positive integer $n$, let $\langle n\rangle$ denote the sum of all the positive divisors of $n$ with the exception of $n$ itself. For example, $\langle 4\rangle=1+2=3$ and $\langle 12 \rangle =1+2+3+4+6=16$. What is $\langle\langle\langle 6\rangle\rangle\rangle?
A. 6B. 12C. 24D. 32E. 36
Answers
For the positive integer n, \(\langle n\rangle\) denote the sum of all the positive divisors of n with the exception of n itself is an option (A). 6.
We start by calculating the value of \(\langle 6 \rangle\), which is the sum of the positive divisors of 6 excluding 6 itself.
Since the divisors of 6 are 1, 2, 3, and 6, we have \(\langle 6 \rangle = 1 + 2 + 3 = 6\).
Next, we need to calculate \(\langle\langle 6 \rangle\rangle\), which is the sum of the positive divisors of 6 excluding 6 itself, and the positive divisors of 6 excluding 6 itself and \(\langle 6 \rangle\).
The divisors of 6 excluding 6 itself are 1, 2, and 3, so \(\langle\langle 6 \rangle\rangle\) is the sum of the positive divisors of 1, 2, and 3.
The divisors of 1 are just 1, the divisors of 2 are 1 and 2, and the divisors of 3 are 1 and 3.
Thus, \(\langle\langle 6 \rangle\rangle = 1 + 2 + 1 + 3 = 7\).
Finally, we need to calculate \(\langle\langle\langle 6\rangle\rangle\rangle\),
which is the sum of the positive divisors of 1, 2, 3, and 7.
The divisors of 1 are just 1, the divisors of 2 are 1 and 2, the divisors of 3 are 1 and 3, and the only divisor of 7 is 1.
Thus, \(\langle\langle\langle 6\rangle\rangle\rangle = 1 + 2 + 1 + 3 + 1 = \boxed{8}\).
For the positive integer n, \(\langle n\rangle\) denote the sum of all the positive divisors of n with the exception of n itself is 6
Hence option A is correct choice.
For similar questions on positive integer
https://brainly.com/question/27761372
#SPJ4
Find the value of (f o g)' at the given value.

Answers
To find the value of (f o g)' at a given value, you first need to understand the concept of composite functions and the chain rule of differentiation. Let's break it down step by step.
To find the value of (f o g)' at a given value, you need to evaluate g(x) and f(x), find their derivatives, and use the chain rule to find the derivative of (f o g) at the given value. It is important to understand the concepts of composite functions and the chain rule to be able to solve problems involving these concepts.
What are composite functions? Composite functions are functions that are formed by composing two or more functions. The notation used to denote composite functions is (f o g)(x), which means that the output of function g is used as the input for function f. In other words, we first evaluate g(x), and then use the result as the input for f(x).
What is the chain rule of differentiation? The chain rule of differentiation is a method used to find the derivative of composite functions. It states that if a function is composed of two or more functions, then its derivative can be found by taking the derivative of the outer function and multiplying it by the derivative of the inner function.
To find the value of (f o g)' at a given value, we need to follow these steps:1. Find g(x) and f(x)2. Find g'(x) and f'(x)3. Evaluate g(x) at the given value4. Use the chain rule to find (f o g)' at the given value
step 1: Find g(x) and f(x)Let's say that we have two functions: g(x) = x^2 + 3x + 1 and f(x) = sqrt(x). To find (f o g)(x), we first need to evaluate g(x) and then use the result as the input for f(x). Therefore, (f o g)(x) = f(g(x)) = sqrt(x^2 + 3x + 1)
Step 2: Find g'(x) and f'(x)To find g'(x), we need to take the derivative of g(x) using the power rule and the sum rule. Therefore, g'(x) = 2x + 3To find f'(x), we need to take the derivative of f(x) using the power rule and the chain rule. Therefore, f'(x) = 1/2(x)^(-1/2)
Step 3: Evaluate g(x) at the given valueSuppose we want to find (f o g)' at x = 2. To do this, we need to first evaluate g(x) at x = 2. Therefore, g(2) = 2^2 + 3(2) + 1 = 11
Step 4: Use the chain rule to find (f o g)' at the given value now we can use the chain rule to find (f o g)' at x = 2. Therefore, (f o g)'(2) = f'(g(2)) * g'(2) = 1/2(11)^(-1/2) * (2)(3) = 3/sqrt(11)
For more such questions on composite
https://brainly.com/question/24820928
#SPJ8
Which statement accurately describes the relationship between JKL and MNP?

Answers
The triangles are not similar
Given data ,
Let the first triangle be ΔJKL
Let the second triangle be ΔMNP
Now , the corresponding sides are
JK / JL ≠ NM / MP
where the corresponding sides of similar triangles are not in the same ratio
And , the common angle to both the triangles is ∠J = ∠M
So , ∠J = ∠M and JK / JL ≠ NM / MP
Hence , the triangles are not similar
To learn more about similar triangles click :
https://brainly.com/question/29378183
#SPJ1
Which equation represents the graphed function?

Answers
Water is added or drained from a tank each day. The first day, 910 of a gallon is added to the empty tank. The second day, 710 of a gallon is drained from the tank. The third day, 810 of a gallon is added to the tank. The fourth day, 610 of a gallon is drained from the tank. how much water is in the tank after 15 days?
Answers
Answer:
200
Step-by-step explanation:
you subtract
Boris is making iced tea. He has a container that has a volume of 7.6 dm3 to hold the iced tea. Find how many kiloliters of iced tea will completely fill the container. Use the table of conversion facts, as needed.
Answers
The capacity of the container is equal to 7.6 × 10⁻³ kiloliters.
How many kiloliters are required to fill a container?
This is a unit conversion question, in which we need to determine how many kiloliters are equivalent to the capacity of a container.
According to capacity tables, a cubic decimeter or 1000 cubic centimeters equals a liter. Then, we can determine the number of kiloliters by using the following cross multiplication:
x = 7.6 dm³ × (1 L / 1 dm³) × (1 kL / 1000 L)
x = 7.6 × 10⁻³ kL
To learn more on unit conversion: https://brainly.com/question/19420601
#SPJ1
Given 1 || m ||
|| n, find the value of x.
(x-6)⁰
60⁰
1
m
n

Answers
The value of x in the lines is 126 degree
We are given that;
Three parallel line and one intersecting line
Angles= (x-6) and 60
Now,
By supplementary angles property
Angle 1 + Angle 2 = 180 degree
Substituting the values of angles
x-6 + 60 = 180
x + 54 = 180
x = 180-54
x = 126
Therefore by supplementary angles answer will be 126 degree.
Learn more about supplementary angles here:
https://brainly.com/question/2882938
#SPJ1
dude what is this i dont understand

Answers
Answer:
g(1) = 1
Step-by-step explanation:
the absolute value function always gives a positive result, that is
| - a | = | a | = a
to evaluate g(1) substitute x = 1 into g(x)
g(1) = - 3| 1 - 2| + 4
= - 3| - 1| + 4
= - 3(1) + 4
= - 3 + 4
= 1
Determine the value of h in the equation 1/5+h=7/5. 6/5 8/25 6/25 8/5
Answers
The value of {h} is equivalent to 6/5.
What is a function?A function, in mathematics, an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).
The domain of a function f(x) is the set of all values for which the function is defined, and the range of the function is the set of all values that function takes.
Given is the function as follows -
(1/5) + h = (7/5)
We can write the function as -
(1/5) + h = (7/5)
h = 7/5 - 1/5
h = (7 - 1)/5
h = 6/5
Therefore, the value of {h} is equivalent to 6/5.
To solve more questions on functions, visit the link below -
brainly.com/question/28135761
#SPJ1
6.(03.02) Write a situation in which positive and negative numbers are used to describe values that have opposite meaning. What does 0 represent in this situation you created?
Answers
Possible Answer 1:
Positive values represent elevations above sea level, while negative values are elevations below sea level. For example, a building may be +100 or simply 100 feet high. Another example: going scuba diving could lead the diver to reach a elevation of -10 meters. The value 0 is the exact location of sea level itself. In other words, if your elevation is 0, then you are at the surface of the water.
==========================================================
Possible Answer 2:
Often in money, loans and borrowing happens. If so, then we use negative numbers to indicate debt. If someone has a bank balance of say -10 dollars, then they owe the bank $10. Positive values mean that they don't owe the money and it's entirely theirs to spend however they want. A balance of 0 means they neither have money, nor do they owe anyone.
==========================================================
Possible Answer 3:
Let's say we define negative distance to mean that you walk some amount to the left (to match up with the fact the negative x values point left). So for instance, we could say the number -14 indicates you walked 14 feet to the left. Positive values on the other hand will mean you walk some amount to the right. Drawing an x axis number line is very recommended. The value 0 indicates that no walking has occurred at all.
==========================================================
Of course, when you write your answer, it should be in your words only. Those answers posted above are just a springboard to get you started.
The equation y=0.28x+3.74 can be used to predict the price of olive oil per quart,
where x is the number of years since 2,000.
According to the model, what will be
the price of olive oil per quart in 2,035?
Round answer to hundredths place. If the
answer doesn't have a hundredths place then include a zero so that the answer
does have an hundredths
Answers
Answer:
44.59 divided by 5.25= 8.49
Hope this helps!!
Answer:
44.5÷56 that how you answer
Selena's dog completed an obstacle course that was 452 meters long. There were four parts to the course, all equal length. How long was each part of the course?
Answers
Answer:
113 meters long
Step-by-step explanation:
If each part is all equal in length, then each part is 1/4 the total length of the obstacle course. Therefore, each part of the course was 1/4(452)=113 meters long