Save Submit Assignment for Grading Exercise 10.04 (Inferences About the Difference Between Two Population Means: Sigmas Known) Question 2 of 13. Hint(s) Condé Nast Traveler conducts an annual survey
Answers
b) Reject the null hypothesis; there is enough evidence to suggest that the readers in Los Angeles gave higher average ratings compared to readers in New York.
Given that Condé Nast Traveler conducts an annual survey, we are provided with the following information: a random sample of 40 readers from Los Angeles gave an average rating of 74.5 with a standard deviation of 2.6, and a random sample of 50 readers from New York gave an average rating of 70.3 with a standard deviation of 2.8.
Additionally, we assume that the population standard deviation for both cities is equal, and the significance level is set at α = 0.01.
To test the claim that readers in Los Angeles gave higher average ratings compared to readers in New York, we need to establish the null hypothesis and alternative hypothesis for this test of significance:
Null Hypothesis: H0: μ1 ≤ μ2 (Readers in Los Angeles gave average ratings less than or equal to readers in New York)
Alternative Hypothesis: H1: μ1 > μ2 (Readers in Los Angeles gave higher average ratings than readers in New York)
Now, with a significance level of α = 0.01, we can calculate the test statistic using the Z-test formula:
Z = ((74.5 - 70.3) - 0) / sqrt [(2.6² / 40) + (2.8² / 50)]
Z = 8.09
Since the sample sizes for both cities are greater than 30, we can utilize the standard normal distribution. Consequently, we can determine the p-value using the Z-table or a calculator. The obtained p-value is less than 0.0001.
Since the obtained p-value is less than the significance level (α = 0.01), we can reject the null hypothesis. Thus, there is sufficient evidence to suggest that readers in Los Angeles gave higher average ratings compared to readers in New York.
Hence, the correct option is b) Reject the null hypothesis; there is enough evidence to suggest that the readers in Los Angeles gave higher average ratings compared to readers in New York.
To learn more about hypothesis, refer below:
https://brainly.com/question/29576929
#SPJ11
Related Questions
What is 8 divided by 1/2
Answers
Answer:
\(8 \div \frac{1}{2} = 8 \times \frac{2}{1} = 8 \times 2 = 16\)
70 = -7 k solve the equations
Answers
Answer:
-10
Step-by-step explanation:
70= -7k
70 -7k
-- --
-7 -7
-10=k
Have a great day
Answer:
k= -10
Step-by-step explanation:
70= -7k
Divide both sides by -7
-7k/-7 = 70/7
Simplify
k=-10
Question is attached. Show workings

Answers
For real and distinct roots of a quadratic a₁v² + a₂v + a₃ = 0, with v the unknown, then the discriminant D > 0 which makes option C correct
Suppose a₁p² + a₂p + a₃ = 0, where a₁, a₂ and a₃ are constants, then the discriminant D = (a₂)² - 4a₁a₃ which makes option C correct.
What is the nature of roots of a quadratic equationThe quadratic equation is of the general form ax² + bx + c = 0 where x is the unknown, a, b and c are constants and the discriminant D = b² - 4ac. The nature of its roots are:
real and distinct if D > 0real and equal if D = 0imaginary or no roots if D < 0For the equation a₁v² + a₂v + a₃ = 0 with real and distinct roots, the discriminant D > 0
For the equation a₁p² + a₂p + a₃ = 0, where a₁, a₂ and a₃ are constants, the discriminant D = (a₂)² - 4a₁a₃.
Therefore, the discriminant D > 0 for the real and distinct roots of the equation a₁v² + a₂v + a₃ = 0. And the discriminant D = (a₂)² - 4a₁a₃ for the quadratic equation a₁p² + a₂p + a₃ = 0
Know more about quadratic equation here:https://brainly.com/question/2507588
#SPJ1
please help me!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
66°
Step-by-step explanation:
Draw the figure to left on a piece of paper and rotate in to fit. I think ∠C = ∠M.
the figures are ≅ so corresponding sizes and angles are ≅.
Simplify (-10c) squared!
Answers
Answer:
-100
Step-by-step explanation:
-10×-10 =-100.
Because square means twice
Answer:
\(\huge\boxed{\sf{100c^2}}\)
Step-by-step explanation:
Hello.
(-10c) squared can be written as
(-10c)²
Now simplify.
First, -10 times -10 is equal to 100.
A negative times a negative is a positiveSo we have
100 times c²
or
100c²
And we're done!
I hope it helps & have an outstanding day!
~ST2710 :)
Let L be the line passing through the point P=(−2, 2, −5) with direction vector →d=[−3, −1, −3]T. Find the shortest distance d from the point P0=(−2, −1, 5) to L, and the point Q on L that is closest to P0.
find d and Q
Answers
The shortest distance (d) between the point P0 and the line L, as well as the closest point Q on L to P0, need to be found.
o find the shortest distance (d) between the point P0 and the line L, we can use the formula that involves the projection of the vector connecting P0 to any point on L onto the direction vector of L.
Find the vector connecting P0 to a point on L: →v = →P0 - →P = [-2 - (-2), -1 - 2, 5 - (-5)] = [0, -3, 10].
Calculate the projection of →v onto the direction vector →d: proj_→d →v = (→v · →d) / ||→d||^2 * →d = (-6 - 3 + 30) / (9 + 1 + 9) * [-3, -1, -3] = [3, 1, 3].
The shortest distance d is the magnitude of the vector →v - proj_→d →v: d = ||→v - proj_→d →v|| = ||[0, -3, 10] - [3, 1, 3]|| = ||[-3, -4, 7]|| = sqrt(74).
The point Q on L that is closest to P0 is found by adding the projection vector to point P: Q = P + proj_→d →v = [-2, 2, -5] + [3, 1, 3] = [1, 3, -2].
Therefore, the shortest distance d from P0 to L is sqrt(74), and the closest point Q on L to P0 is (1, 3, -2).
Learn more Vector click here :brainly.com/question/13322477
#SPJ11
Arianne is 6 years older than jan.six years ago she was twice as old as he.how old is each now?
Answers
integral of 1/sqrt(x^2 - a^2) dx
Answers
To solve the integral of 1/sqrt(x^2 - a^2) dx, we can use the substitution method. Let u = x^2 - a^2, then du/dx = 2x, and dx = du/2x.
Substituting into the integral, we get:
∫ 1/sqrt(x^2 - a^2) dx = ∫ 1/sqrt(u) * du/2x
= (1/2) ∫ 1/sqrt(u) du
= (1/2) * 2sqrt(u) + C
= sqrt(x^2 - a^2) + C
Therefore, the answer to the integral of 1/sqrt(x^2 - a^2) dx is sqrt(x^2 - a^2) + C, where C is the constant of integration.
In summary, the integral of 1/sqrt(x^2 - a^2) dx can be solved using the substitution method, where u = x^2 - a^2. The final answer is sqrt(x^2 - a^2) + C, where C is the constant of integration.
To know more about substitution method visit :-
https://brainly.com/question/12688945
#SPJ11
The integral of \(\frac{1}{\sqrt{x^2 - a^2}} dx\) is \(\ln\left|\frac{\sqrt{x^2 - a^2}}{a} + \frac{x}{a}\right| + C\), where C is the constant of integration
What is intergration?
Integration is a fundamental concept in calculus that involves finding the antiderivative or integral of a function. It is the reverse process of differentiation, which is concerned with finding the derivative of a function.
To find the integral of \(1/\sqrt(x^2 - a^2) dx\), we can use a trigonometric substitution. Let's substitute \(x = a sec(\theta)\), where \(sec(\theta)\) is the reciprocal of the cosine function.
By making this substitution, we can express dx in terms of \(d(\theta)\) as follows:
\(dx = a sec(\theta) tan(\theta) d(\theta)\)
Now, let's substitute these values into the integral:
\(\int \frac{1}{\sqrt{x^2 - a^2}} dx\\\\= \int \frac{1}{\sqrt{(a \sec(theta))^2 - a^2}} (a \sec(\theta) \tan(\theta)) d(\theta)\\\\= \int \frac{1}{\sqrt{a^2(\sec^2(theta) - 1)}} (a \sec(\theta) \tan(\theta)) d(\theta)\\\\= \int \frac{1}{\sqrt{a^2(\tan^2(theta))}} (a \sec(\theta) \tan(\theta)) d(\theta)\\\\= \int \frac{1}{a \tan(theta)} (a \sec(\theta) \tan(\theta)) d(\theta)\)
Simplifying the expression, we have:
\(= \int \sec(\theta) d(\theta)\)
The integral of \(sec(\theta)\) can be evaluated as the natural logarithm of the absolute value of \(sec(\theta)\) plus the tangent\((\theta)\):
\(= \ln|\sec(\theta) + \tan(\theta)| + C\)
Finally, substituting back \(x = a sec(\theta)\), we get:
\(= \ln|\sec(\theta) + \tan(\theta)| + C\\\\= \ln\left|\frac{\sqrt{x^2 - a^2}}{a} + \frac{x}{a}\right| + C\)
Therefore, the integral of \(\frac{1}{\sqrt{x^2 - a^2}} dx\) is \(\ln\left|\frac{\sqrt{x^2 - a^2}}{a} + \frac{x}{a}\right| + C\), where C is the constant of integration
To learn more about integration visit:
https://brainly.com/question/27419605
#SPJ4
The shadow of a tower is equal to its height at 10.45 a.m. The sun’s altitude is
Answers
Incomplete question.
please help i’ll give brainlist to anyone

Answers
Answer:
well i cant really tell so much though
Step-by-step explanation:
what is the volume of the prism?
enter your answer in the box as a mixed number in simplest form.

Answers
Answer:
67 1/2 cm
Step-by-step explanation:
v=lxwxh
v=4 1/2x 6x 2 1/2
v=67 1/2 cm^3
Volume of rectangular prism is given by:
ㅤㅤㅤ➙ V = l × b × h
Here, we have :
length = 6 cmBreadth =\( \sf{2\dfrac{1}{2}}\)cm.height =\(\sf{4\dfrac{1}{2}} \)cmTherefore, volume:
\( \implies\quad \tt {V =l\times b\times h }\)
\( \implies\quad \tt { V =6\times 2\dfrac{1}{2}\times 4\dfrac{1}{2}}\)
\( \implies\quad \small{\tt { V = 6\times \dfrac{(2\times 2)+1}{2}\times \dfrac{(4\times 2)+1}{2}}}\)
\( \implies\quad \tt {V = 6\times \dfrac{4+1}{2}\times \dfrac{8+1}{2} }\)
\( \implies\quad \tt {V =6\times \dfrac{5}{2}\times\dfrac{9}{2} }\)
\( \implies\quad \tt {V =\dfrac{6\times 5\times 9}{2\times 2} }\)
\( \implies\quad \tt { V =\cancel{\dfrac{270}{4}}}\)
\( \implies\quad \tt { V = \dfrac{135}{2}}\)
\( \implies\quad \underline{\underline{\pmb{\tt { V = 67\dfrac{1}{2}\:cm^2}}}}\)
The height of a triangle is 3 inches less than twice the length of its base. If the total area of the triangle is 7 square inches, find the length of the base and height.
Answers
Answer:
Let x be the length of the base of the triangle, then the height h is given by h = 2x - 3 (since the height is 3 inches less than twice the length of the base).
The area of a triangle is given by the formula A = (1/2)bh, where b is the base and h is the height. We are given that the total area of the triangle is 7 square inches, so we can write:
(1/2)(x)(2x - 3) = 7
Multiplying both sides by 2 to eliminate the fraction, we get:
x(2x - 3) = 14
Expanding the left side, we get:
2x^2 - 3x = 14
Subtracting 14 from both sides, we get:
2x^2 - 3x - 14 = 0
We can now use the quadratic formula to solve for x:
x = (-b ± sqrt(b^2 - 4ac))/(2a)
where a = 2, b = -3, and c = -14. Plugging in these values, we get:
x = (-(-3) ± sqrt((-3)^2 - 4(2)(-14)))/(2(2))
= (3 ± sqrt(169))/4
= (3 ± 13)/4
Taking the positive value for x (since the length of the base must be positive), we get:
x = (3 + 13)/4
= 4
Therefore, the length of the base is 4 inches. To find the height h, we can use the formula h = 2x - 3:
h = 2(4) - 3
= 5
So the height of the triangle is 5 inches.
Find the volume and surface area of the figure.

Answers
The surface area and volume of the trianglular prism are 179.2m² and 492.8m³ respectively.
How to calculate the surface area and volume of the trianglular prismarea of one trianglular face = 1/2 × 8m × 11.2m
area of one trianglular face = 44.8m²
surface area of the trianglular prism = 4 × 44.8m²
surface area of the trianglular prism = 179.2m²
Volume of triangular prism = base area × height
base area of prism = 1/2 × 8m × 11.2m
base area of prism = 44.8m²
volume of the trianglular prism = 44.8m² × 11m
volume of the trianglular prism = 492.8m³
Therefore, the surface area and volume of the trianglular prism are 179.2m² and 492.8m³ respectively.
Read more about triangular prism here:https://brainly.com/question/12591701
#SPJ1
Find the difference between (x + 5) and (2x + 3) *
Answers
Answer:
x -2.
Step-by-step explanation:
Given : (x + 5) and (2x + 3).
To find : Find the difference between .
Solution : We have given (x + 5) and (2x + 3).
According to question :
Difference of (x + 5) and (2x + 3).
(2x + 3) - (x +5).
2x + 3 - x - 5 .
On combine like terms.
2x -x +3 -5.
x -2.
Therefore, x -2.
The difference between (x + 5) and (2x + 3) is -x + 2
what's difference :Difference is the result of subtracting one number from another. Therefore,
the difference between (x + 5) and (2x + 3) can be calculated below:
(x + 5) - (2x + 3)Open the bracket with the minus sign
Therefore,
x + 5 - 2x - 3
combine like terms
x - 2x + 5 - 3
-x + 2
Therefore, the difference between (x + 5) and (2x + 3) is -x + 2
learn more on difference here:https://brainly.com/question/2636246?referrer=searchResults
how to find the leading coefficient of a polynomial?
Answers
A polynomial is represented as \(\mathbf{ax^n + bx^{n-1} + cx^{n-2} + .... + d}\)
The leading coefficient of the polynomial is "a"
The leading coefficient of a polynomial is simply the coefficient of the variable with the highest power.
Take for instance:
\(\mathbf{2x^3 + 4x^2 + 5x - 6}\)
In the above polynomial,
The highest power is 3The variable is xThe coefficient of x is 2, when the highest power is 3This means that, the leading coefficient is 2
Another instance:
\(\mathbf{-6y^5 + 2y^4 + 19y^3 - y^2 -17y + 1}\)
In the above polynomial,
The highest power is 5The variable is yThe coefficient of y is -6, when the highest power is 5This means that, the leading coefficient is -6
In general,
The leading coefficient of the polynomial \(\mathbf{ax^n + bx^{n-1} + cx^{n-2} + .... + d}\) is "a"
Read more about leading coefficients at:
https://brainly.com/question/15323309
1 + 1???????????????????
Answers
Answer:
2
Hopefully that's the answer you wanted XD
Answer:
2
Step-by-step explanation:
a least squares linear trend line is just a simple regression line with the years recoded. group of answer choices true false
Answers
a least squares linear trend line is just a simple regression line with the years recoded then it is a true statement
The simple linear regression model is;
y = mx + c
Where,
y = dependent variable
m is the slope
x is the independent variable
c is the y- intercept
The long-term trend only Least-Squares Regression Model also follows the same format except y becomes Yt and x becomes t.
The long-term trend only Least-Squares Regression Model is therefore the same as a simple linear regression only with different variable terms.
learn more about of square here
https://brainly.com/question/19595237
#SPJ4
(b) Given the matrix D = k 0 0 3 k² k³ 0 kª k³ kº k k k 0 0 0 k¹⁰ Find all possible value(s) of k if det(D) = 1024."
Answers
To find the possible values of k, we need to calculate the determinant of matrix D and set it equal to 1024.
Given matrix D:
D = | k 0 0 |
| 3 k² k³ |
| 0 kª k³ kº |
| k k k |
| 0 0 0 |
| k¹⁰ |
The determinant of D can be calculated by expanding along the first row or the first column. Let's expand along the first row:
det(D) = k(det | k³ k k |
| 0 k³ kº |
| 0 0 k¹⁰ |)
- 0(det | 3 k² k³ |
| 0 kª k³ |
| k k k |)
+ 0(det | 3 k² k³ |
| k k k |
| k k k |)
Simplifying further, we have:
det(D) = k(det | k³ k k |
| 0 k³ kº |
| 0 0 k¹⁰ |)
Now, we can calculate the determinant of the 3x3 submatrix:
det | k³ k k |
| 0 k³ kº |
| 0 0 k¹⁰ |
This determinant can be found by expanding along the first row or the first column. Expanding along the first row gives us:
det = k(k³(kº) - 0(k)) - 0(0(k¹⁰)) = k⁴kº = k⁴+kº
Now, we can set det(D) equal to 1024 and solve for k:
k⁴+kº = 1024
Since we are looking for all possible values of k, we need to solve this equation for k. However, solving this equation may require numerical methods or approximations, as it is a quartic equation.
Learn more about matrix here
https://brainly.com/question/2456804
#SPJ11
Taylor was asked to solve the system of linear equations
3x - y = 12 and 10x + 5y = -10
by substitution. His solution is shown below.
Taylor's Solution:
Line 1: 10x + 5(-3x + 12)=-10
Line 2:10x - 15x + 60 = -10
Line 3: -5x +60 = -10
Line 4: -5x = -10 - 60
Line 5: -5x = -70
Line 6: x = 14
Which line is wrong? (pls help I’ll mark as brainliest)

Answers
what proportion of the variation in y can be explained by the variation in the values of x? report answer as a percentage accurate to one decimal plac
Answers
The relation R is not reflexive, but it is symmetric and transitive.
What is transitivity?A homogeneous relation R over the set A, which comprises the elements x, y, and z, is known as a transitive relation. If R relates x to y and y to z, then R likewise relates x to z.
For x, y ∈ Z, xRy if and only if (x+y)² ≡ ±1.
(a) Reflexivity: For x ∈ Z, we have (x + x)² = 4x² ≡ 0 (mod 1), which is not equal to ±1. Therefore, xRx does not hold for any x ∈ Z, and R is not reflexive.
(b) Symmetry: For x, y ∈ Z, if xRy, then (x + y)² ≡ ±1. This implies that (y + x)^2 ≡ (x + y)² ≡ ±1. Therefore, yRx also holds, and R is symmetric.
(c) Transitivity: For x, y, z ∈ Z, if xRy and yRz, then (x + y)² ≡ ±1 and (y + z)² ≡ ±1. Expanding these expressions, we get:
(x + y)² ≡ ±1 => x² + 2xy + y² ≡ ±1
(y + z)² ≡ ±1 => y² + 2yz + z² ≡ ±1
Adding these two equations, we get:
x² + 2xy + y² + y² + 2yz + z² ≡ ±2
Simplifying, we get:
x² + 2xy + 2yz + z² ≡ ±2 - 2y²
Now, we need to show that (x + z)² ≡ ±1. Expanding (x + z)², we get:
(x + z)² = x² + 2xz + z²
Substituting x² + 2xy + 2yz + z² ≡ ±2 - 2y², we get:
(x + z)² ≡ 2 - 2y² + 2xz
To complete the proof, we need to show that there exists some integer k such that 2 - 2y² + 2xz - k² ≡ ±1. We can rewrite this expression as:
2xz - k² ≡ 2y² - 3 (mod 4)
Since the left-hand side is even, the right-hand side must also be even. Therefore, y² ≡ 1 (mod 4), which implies that y is odd.
Now, we can substitute y = 2m + 1 for some integer m, and simplify:
2xz - k² ≡ 8m² + 8m - 1 (mod 4)
We can rewrite the right-hand side as 4(2m² + 2m) - 1, which is congruent to -1 (mod 4). Therefore, there exists some integer k such that 2xz - k² ≡ ±1, which implies that (x + z)² ≡ ±1. Hence, xRz holds, and R is transitive.
In summary, the relation R is not reflexive, but it is symmetric and transitive.
Learn more about reflexivity on:
https://brainly.com/question/25687310
#SPJ4
Simplify the following expressions
a. 2/5- 1/6 b. 3/7-7/14 c. 5/8- 2/3
Answers
Multiply the denominator until both denominators are the same
12/30 - 5/30
Subtract the numerator but NOT the denominator
Final Answer: 7/30
2.) 3/7-7/14
Multiply the denominator until both denominators are the same common denominator
6/14 - 7/14
Subtract the numerator but NOT the denominator
Final Answer: -1/14
3.) 5/8-2/3
Multiply the denominator until both denominators are the same
15/24 - 16/24
Subtract the numerator but NOT the denominator
Final Answer: -1/24
if a cubic box (all sides the same length) has a volume of 1.0 l, what is the length of each side of the box in cm?
Answers
The length of each side of the box is 10 centimeter.
Volume is the amount of space occupied by a three-dimensional figure as measured in cubic units.
Given,
The volume of the cubic box = 1 liter
We know 1 liter= 1000 cubic centimeter
Volume of the cubic box= \(x^3}\)
Then,
\(x^{3}=1000\\ x=\sqrt[3]{1000}\)
x=10 centimeter
Hence, the length of each side of the box is 10 centimeter.
Learn more about volume here
brainly.com/question/1578538
#SPJ4
What is the solution to the equation 4.82y = 156.891?

Answers
Answer:
The answer to this is B. y=32.55
Yu, Nailah, and Elena each bought between 7 and 9 yards of ribbon. Yu bought 3 pieces of ribbon. Nailah bought 5 pieces of ribbon. Elena bought 6 pieces of ribbon. The lengths of ribbons are given below. Drag ribbons to the box below each person's name to show what they could have bought. length of ribbons- 1 2/3yd 4/5yd 3 1/2yd
Answers
Answer:
Elena = 3 1/2 yards
Nailah = 1 2/3 yards
Yu = 4/5 yards
Step-by-step explanation:
Pieces of ribbon purchased :
Yu - 3 pieces
Nailah - 5 pieces
Elena - 6 pieces
We could infer that ;
Elena who bought 6 pieces or ribbon bought the highest amount of ribbon followed by Nailah, then Yu
Given that the number of yards each of Yu, Elena and Nailah could have bought :
1 2/3yd ; 4/5yd ; 3 1/2yd
Elena bought the highest number of prices and hence would possibly have the highest number of yards = 3 1/2
Nailah bought next, with 5 pieces, which is greater than Number of pieces bought by Yu but less than Elena ; hence, she could have bought 1 2/3 yards
Then Yu who has the least could have 4/5 yards
900 students attend Ridgewood Junior High School. 4% of students bring their lunch to school everyday. How many students brought their lunch to school on Thursday?
Answers
1. Write out the problem
4/100 ?/900
2. Start to multiply the numbers
4 x 900 = 3,600
3. Divide the number by 100
3,600 divided by 100 equals 36.
Your answer is 36. So 36 students brought their lunch to school on Thursday.
I hope this helps.

Trying to get the right number possible. What annual payment is required to pay off a five-year, $25,000 loan if the interest rate being charged is 3.50 percent EAR? (Do not round intermediate calculations. Round the final answer to 2 decimal places.Enter the answer in dollars. Omit $sign in your response.) What is the annualrequirement?
Answers
To calculate the annual payment required to pay off a five-year, $25,000 loan at an interest rate of 3.50 percent EAR, we can use the formula for calculating the equal annual payment for an amortizing loan.
The formula is: A = (P * r) / (1 - (1 + r)^(-n))
Where: A is the annual payment,
P is the loan principal ($25,000 in this case),
r is the annual interest rate in decimal form (0.035),
n is the number of years (5 in this case).
Substituting the given values into the formula, we have:
A = (25,000 * 0.035) / (1 - (1 + 0.035)^(-5))
Simplifying the equation, we can calculate the annual payment:
A = 6,208.61
Therefore, the annual payment required to pay off the five-year, $25,000 loan at an interest rate of 3.50 percent EAR is $6,208.61.
Learn more about loan here: brainly.com/question/32625768
#SPJ11
PLEASE HELP ASAP!!!!
Based on the information in the two-way table, what is the
probability that a person selected at random both bikes and
runs?
Round your answer to the nearest tenth of a percent.
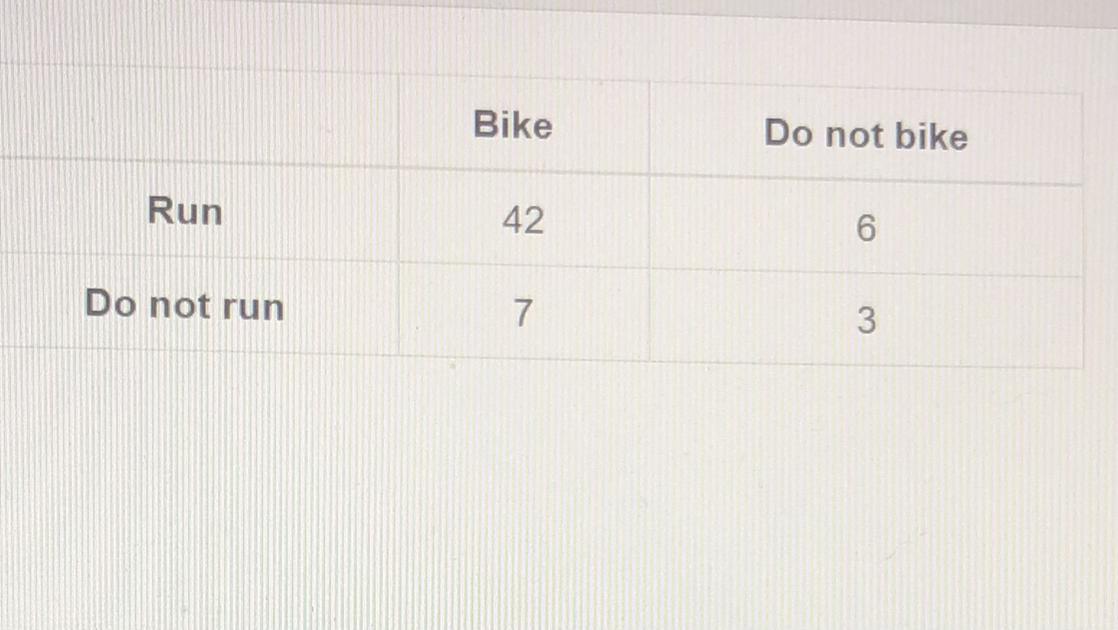
Answers
Answer:10
Step-by-step explanation:
a rectangular prism is filled exactly with 248 cubes. the edge length of each cube is 12 cm. what is the volume of the rectangular prism?
Answers
The volume of the rectangular prism is 428,544 cubic cm.
To find the volume of the rectangular prism, we can start by determining the dimensions of the prism.
Let's assume the length, width, and height of the prism are L, W, and H, respectively.
Given that the rectangular prism is filled exactly with 248 cubes, we can express the total number of cubes as the product of the length, width, and height of the rectangular prism:
\(L \times W \times H = 248\)
Since each cube has an edge length of 12 cm, the volume of one cube can be calculated as follows:
Volume of one cube \(= (12 cm) \times (12 cm) \times(12 cm)\)
Volume of one cube \(= 1728 cm^3\)
Now, we can set up the equation based on the given information:
\(L \times W \times H = 248 \times Volume of one cube\)
\(L \times W \times H = 248 \times 1728 cm^3\)
To find the volume of the rectangular prism, we need to calculate the right side of the equation:
\(248 \times1728 = 428,544 cm^3\)
Therefore, the volume of the rectangular prism is \(428,544 cm^3\).
For such more questions on rectangular prism
https://brainly.com/question/24284033
#SPJ8
Wat is the value of x 0.25 + 13= 4(x- 8
Answers
Answer:
x = 11.3125
Step-by-step explanation:
0.25 + 13 = 4(x - 8)
Distribute the 4 across the parentheses.
0.25 + 13 = 4x - 32
Combine the constants on the left side of the equal sign.
13.25 = 4x - 32
Combine all the constants by adding 32 to both sides.
45.25 = 4x
Divide by 4 to isolate the x.
45.25/4 = x
11.3125 = x
Check.
0.25 + 13 = 4(x - 8)
0.25 + 13 = 4(11.3125 - 8)
0.25 + 13 = 4(3.3125)
0.25 + 13 = 13.25
13.25 = 13.25
write an expression for 8 less than 2 times a number
show your work
Answers
Answer:
Step-by-step explanation:
Let's call the number x. The statement "...2 times a number" if the number is x looks like this:
2x
"8 less than" that looks like this:
... - 8
Putting the whole thing together:
2x - 8