Sand is being dumped from a conveyor belt and forms a conical pile. Assuming that the height of this cone is always exactly 3 times the size of the radius of its base, and that thesand is added at the rate of 10 m^3/min, how fast is the height increasing when the pile is15 m high?
Answers
Answer:
dh/dt = 0.4 m/min
Step-by-step explanation:
The volume of the cone is:
V(c) = (1/3)*r² *h if always h = 3r then r = h/3
The volume of the cone as a function of h will be:
V(h) = (1/3)* (h/3)²*h
V(h) = (1/27)*h³
The increasing rate of the volume is equal to the rate of sand added the:
D(V)/dt = (1/27)*3*h²*dh/dt
D(v) / dt = 10 m³/min
h = 15 m and dh/dt is the rate of increasing of the height
By substitution
10 m³/min = ( 1/9)* 225 * dh/dt (m²)
dh/dt = 90 / 225 m/min
dh/dt = 0.4 m/min
Related Questions
What numbers are equivalent to 25%
Answers
Answer:
0.25 decimal
1/4 decimal
Step-by-step explanation:
What is photosynthesis?
Answers
▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓\(\pmb{\qquad{\qquad{\underline{\green{\underline{\sf{Photosynthesis}}}}}}}\)
Photosynthesis is the process by which green plants take in carbon dioxide and water, in the presence of chlorophyll by using sunlight to make their own food. Oxygen is released as a by product.
Chemical Reaction for PHOTOSYNTHESIS:
\(\sf 12H_2O + 6CO_2 \underset{chlorophyll}{\xrightarrow{Sunlight}} C_6H_{12}O_6 + 6H_2O + 6O_2 \uparrow\)▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓
In the figure below, point B is the corner of street ABC. If streetlights are to b
installed along one side of the street with equal distance between the lights, and a
treetlight must be installed at points A, B and C, at least how many streetlights
an be installed along the street?
A
1625 m
B
cli
1170 m

Answers
Therefore, at least 49 street lights can be installed along one side of the street with equal distance between the lights.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It consists of two parts: the left-hand side (LHS) and the right-hand side (RHS), separated by an equals sign (=). The equals sign indicates that the two expressions are equal, and the goal of solving the equation is to find the value of x that makes this statement true. Equations can be solved using various algebraic techniques, such as simplifying and rearranging the expressions, applying operations to both sides of the equation, and factoring or expanding expressions. Solving an equation involves finding the values of the variables that make the equation true.
Here,
The distance between point A and B is AB, and the distance between point B and C is BC. Let's assume that the distance between each street light is "d".
Since there must be a street light at points A, B, and C, there will be a total of two gaps between these three street lights, which are AB and BC. Thus, the number of street lights required is equal to the sum of the lengths of AB and BC, divided by the distance "d" between the street lights, plus 1 for the street light at point B.
So, the total number of street lights required is
Number of street lights = (AB + BC) / d + 1
We know that AB = 1170 m and BC = 1625 m, and the distance between each street light should be equal. Therefore, we need to find the greatest common factor (GCF) of 1170 and 1625 to determine the distance between each street light.
1170 = 2 x 3 x 3 x 5 x 13
1625 = 5 x 5 x 13
The GCF of 1170 and 1625 is 65, which means the distance between each street light should be 65 meters.
Now we can calculate the total number of street lights required:
Number of street lights = (1170 + 1625) / 65 + 1
= 49
To know more about equation,
https://brainly.com/question/28243079
#SPJ9
Select the correct answer.
Which pair of statements correctly compares the two data sets?
A.
The difference of the means is 1. This value is less than half of the mean absolute deviation of either data set.
B.
The difference of the means is 1. This value is more than half of the mean absolute deviation of either data set.
C.
The difference of the means is 1. This value is 1 times the mean absolute deviation of either data set.
D.
The difference of the means is 1. This value is 2 times the mean absolute deviation of either data set.

Answers
Answer:
Step-by-step explanation:
Do you still need help?
Find an equation of the sphere with center (4, −12, 8) and radius 10.Use an equation to describe its intersection with each of the coordinate planes. (If the sphere does not intersect with the plane, enter DNE.)intersection with xy-plane intersection with xz-plane intersection with yz-plane
Answers
The equation of the sphere with center coordinates (4, −12, 8) and radius 10 is x² -8x + y² + 24y + z² -16z + 124 =0 .
And different plane equations are :
Intersection with xy-plane : ( x - 4 )² + ( y + 12 )² = 6²
Intersection with yz plane :( y + 12 )² + ( z - 8 )² = (√84)²
Intersection with zx plane :( x - 4 )² + ( z - 8 )² = -44
Equation of the sphere with center coordinates (4, −12, 8) and radius 'r' = 10 is :
( x - 4 )² + ( y + 12 )² + ( z - 8 )² = 10²
⇒ x² -8x + y² + 24y + z² -16z + 224 = 100
⇒x² -8x + y² + 24y + z² -16z + 124 =0
Intersection with xy-plane
z = 0
( x - 4 )² + ( y + 12 )² + ( 0 - 8 )² = 10²
⇒( x - 4 )² + ( y + 12 )² = 6²
Circle with center ( 4,-12) and radius 6.
Intersection with yz-plane
x = 0
( 0 - 4 )² + ( y + 12 )² + ( z - 8 )² = 10²
⇒( y + 12 )² + ( z - 8 )² = (√84)²
Circle with center ( -12, 8) and radius √84.
Intersection with zx-plane
y = 0
( x - 4 )² + ( 0 + 12 )² + ( z - 8 )² = 10²
⇒( x - 4 )² + ( z - 8 )² = -44
Not possible as radius cannot be negative.
Therefore, the equation of the sphere with the given center and radius is equal to x² -8x + y² + 24y + z² -16z + 124 =0 and equation of the intersection of different planes are:
xy-plane : ( x - 4 )² + ( y + 12 )² = 6²
yz plane :( y + 12 )² + ( z - 8 )² = (√84)²
zx plane :( x - 4 )² + ( z - 8 )² = -44
Learn more about sphere here
brainly.com/question/12390313
#SPJ4
Two skateboarders start a race at the same time. Skateboarder A travels at a steady rate of 15 feet per second. Skateboarder B travels at a steady rate of 22 feet per second. After 4 minutes, how much farther will Skateboarder B have traveled? Explain your reasoning.
Answers
Answer:
Skateboarder B will have traveled 1,680 feet farther.
Step-by-step
Possible reasoning: There are 240 seconds in 4 minutes
construct a polynomial function with least degree possible with real roots:-1/2,0,1/2 and (-2,f(-2))=(-2,6)
Answers
9514 1404 393
Answer:
f(x) = -0.8x^3 +0.2x
Step-by-step explanation:
For root 'a', one of the factors will be (x-a). For the three given roots, the factored form of the polynomial can be written ...
f(x) = c(x -(-1/2))(x-0)(x -1/2) = cx(x^2 -1/4)
Then for x=-2, the value is ...
f(-2) = c(-2)((-2)^2 -1/4) = -7.5c
f(-2) = 6 = -7.5c
c = -6/7.5 = -0.8
Then the polynomial can be written as ...
f(x) = -0.8x^3 +0.2x

p(x)=5x^4+7x^3-2x^2-3x+c divided by (x+1)
Answers
The remainder is 5 + c, which means that the expression P(x) = \(5x^4 + 7x^3 - 2x^2 - 3x + c\) divided by (x + 1) results in a quotient of\(5x^3 + 2x^2 - 4x + 4\) and a remainder of 5 + c.
To divide the polynomial P(x) = \(5x^4 + 7x^3 - 2x^2 - 3x + c\) by the binomial (x + 1), we can use polynomial long division.
Let's set up the long division:
\(5x^3 + 2x^2 - 4x + 4\)
_______________________
x + 1 | \(5x^4 + 7x^3 - 2x^2 - 3x + c\)
We start by dividing the highest degree term of the dividend (5x^4) by the divisor (x + 1), which gives us 5x^3. We then multiply this quotient by the divisor (x + 1) and subtract it from the dividend:
\(5x^3(x + 1)\)
_______________________
x + 1 | \(5x^4 + 7x^3 - 2x^2 - 3x + c\)
- (\(5x^3 + 5x^2)\)
This leaves us with a new polynomial:\(2x^3 - 7x^2 - 3x + c\). We repeat the process by dividing the highest degree term of this polynomial (2x^3) by the divisor (x + 1), resulting in 2x^2. We then multiply this quotient by the divisor and subtract it from the polynomial:
\(5x^3(x + 1) + 2x^2(x + 1)\)
_______________________
x + 1 | \(5x^4 + 7x^3 - 2x^2 - 3x + c\)
-\((5x^3 + 5x^2)\)
_______________________
\(2x^2 - 3x + c\)
We continue this process until we reach the constant term, resulting in the remainder of the division.
At this point, we have:
\(5x^3(x + 1) + 2x^2(x + 1)\)
_______________________
x + 1 | \(5x^4 + 7x^3 - 2x^2 - 3x + c\)
- \((5x^3 + 5x^2)\)
_______________________
\(2x^2 - 3x + c\)
-\((2x^2 + 2x)\)
_______________________
- 5x + c
- (-5x - 5)
_______________________
5 + c
For more such questions on remainder visit:
https://brainly.com/question/29347810
#SPJ8
PV = $250,000 / (1+0.065)^1 + $37,500 / (1+0.065)^2 + $180,000 / (1+0.065)^3 + $300,000 / (1+0.065)^4 + $750,000 / (1+0.065)^5 + $725,000 / (1+0.065)^6
Answers
The given expression represents the present value of a series of future cash flows discounted at a rate of 6.5% per year.
Each term in the expression represents a cash flow at a specific time in the future, and the denominator in each term represents the discount factor, which reflects the time value of money.
The first term, $250,000 / (1+0.065)^1, represents a cash flow of $250,000 that will be received in one year.
To determine its present value, we divide it by the discount factor (1+0.065)^1, which reflects the fact that the money will be received one year from now and is, therefore, less valuable than money received today.
Similarly, the second term, $37,500 / (1+0.065)², represents a cash flow of $37,500 that will be received in two years.
To determine its present value, we divide it by the discount factor (1+0.065)²,
which reflects the fact that the money will be received two years from now and is, therefore, less valuable than money received today.
This process is repeated for each term in the expression, representing cash flows that will be received in three, four, five, and six years, respectively.
The sum of these present values represents the total present value of the cash flows or the amount that they are worth today if they are discounted at a rate of 6.5% per year.
Learn more about Simplification here:
https://brainly.com/question/28996879
#SPJ1
This is about scatter plots and association i just need number 1

Answers
The form of association that would be found in the variables would be:
Positive association No association Negative association How to find the association ?As the number of hours spent playing a video game increases, the player is likely to reach higher levels within the game. So positive association.
The number of letters in a person's name and the last digit of their phone number are likely to be unrelated and randomly distributed. There is no association.
As the temperature of the drink decreases, the number of ice cubes in the drink is likely to increase, and vice versa. This is therefore negative association.
Find out more on negative association at https://brainly.com/question/29264211
#SPJ1
Jessica needs to know how much water her new fish tank can hold:
A rectangular prism with a length of 8 inches, a width of 4 inches, and a height of 9 inches.
Determine the total volume of the fish tank.
Answers
The fish tank has a total volume of 288 inch³. As a result, Jessica's new fish tank has a capacity of 288 inch³ for water.
The volume of a rectangular prism can be calculated using the formula:
V = l x b x h..........(i)
where,
V ⇒ Volume
l ⇒ length
b ⇒ width
h ⇒ height
From the question, we are given the values,
l = 8 inches
b = 4 inches
h = 9 inches
Putting these values in equation (i), we get,
V = 8 x 4 x 9
⇒ V = 288 in³
Therefore, the fish tank has a total volume of 288 inch³. As a result, Jessica's new fish tank has a capacity of 288 inch³ for water.
Learn more about the volume of rectangular prism on:
https://brainly.com/question/24284033
Angle TLN equals (3X -18)°, angle MZQ equals (5X +14)° and

Answers
For the given figure, x = 23° and y = 129°
Parallel lines:
Parallel lines are lines that always stay the same distance apart and never meet.
Transversal line :
A transversal is a line that crosses two or more other lines.
given,
∠TLN = (3x - 18)°
∠MZQ = (5x + 14)°
∠NLM = y°
Now,
∠MZP + ∠MZQ = 180° (Linear Pair)
∠MZP = 180° - ∠MZQ ...........(I)
again,
∠NLM + ∠TLN =180° ...........(II) (Linear Pair)
As, ∠TLN = ∠MZP (Corresponding Angle)
(3x - 18)° = 180° - ∠MZQ
(3x - 18)° = 180° - (5x + 14)°
3x + 5x = 180° - 14° + 18°
8x = 184°
x = 184 / 8
x = 23°
From (II),
∠NLM + ∠TLN =180°
y° + 3x - 18° = 180°
y = 180 - 3x + 18
= 180 - 3* 23 + 18
= 180 - 69 +18
y = 129°
For the given figure,
x = 23° and y = 129°
To learn more about Parallel line visit:
https://brainly.com/question/17432060
#SPJ9
19 - a = 42
What is a?
Answers
Answer:
61
Step-by-step explanation:
add 42 the 19 because of reverse operation
Someone help me with this

Answers
Answer:
Step-by-step explanation:

In 2015, the average distance from Earth to the moon was about 3.74 x 105 km. The distance from Earth to Mars was about 9.25 x 107 km. How much farther is traveling from Earth to Mars than from Earth to the moon? Write your answer in scientific notation.
Answers
Traveling from Earth to Mars is approximately 9.249626 x 10^7 km farther than traveling from Earth to the moon.
Earth to Mars is compared to traveling from Earth to the moon, we need to calculate the difference between the distances.
The distance from Earth to the moon is approximately 3.74 x 10^5 km.
The distance from Earth to Mars is approximately 9.25 x 10^7 km.
To find the difference, we subtract the distance to the moon from the distance to Mars:
9.25 x 10^7 km - 3.74 x 10^5 km
To subtract these numbers, we need to make sure the exponents are the same. We can rewrite the distance to the moon in scientific notation with the same exponent as the distance to Mars:
3.74 x 10^5 km = 0.374 x 10^6 km (since 0.374 = 3.74 x 10^5 / 10^6)
Now we can perform the subtraction:
9.25 x 10^7 km - 0.374 x 10^6 km = 9.25 x 10^7 km - 0.374 x 10^6 km
To subtract, we subtract the coefficients and keep the same exponent:
9.25 x 10^7 km - 0.374 x 10^6 km = 9.25 x 10^7 - 0.374 x 10^6 km
Simplifying the subtraction:
9.25 x 10^7 - 0.374 x 10^6 km = 9.249626 x 10^7 km
Therefore, traveling from Earth to Mars is approximately 9.249626 x 10^7 km farther than traveling from Earth to the moon.
Scientific notation is a convenient way to express very large or very small numbers. It consists of a coefficient (a number between 1 and 10) multiplied by a power of 10 (exponent). It allows us to write and manipulate such numbers in a compact and standardized form.
To know more about Traveling .
https://brainly.com/question/21219866
#SPJ11
Chris needs a total of $340 to buy a new bicycle. He has $40 saved. He earns $15 each week delivering newspapers. How many weeks will Chris have to deliver papers to have enough money to buy the bicycle?
Answers
Answer: 20 weeks
Step-by-step explanation:
340 - 40 = 300
15 (w)
300 / 15 = 20
15 (20) = 300
There is a 6.5% tax on a $750 refrigerator. How much is paid
altogether for the refrigerator?
Answers
Answer:
The total price of the refrigerator is $798.75.
Step-by-step explanation:
6.5% of $750 is $48.75
So, $750 plus $48.75 equals $798.75.
OKK PLEASE HELP if correct will give brainliest help and 5 star pls help by 1230 pt

Answers
To increase an amount by 30%, what single multiplier would you use? and To decrease an amount by 30%, what single multiplier would you use?
Answers
Answer:
To increase, use 1.3
to decrease, use .7
Step-by-step explanation
WILL MARK BRAINLY!
Which inequality is true?
1-100 < 50
--50 100
1-100 > 50
4-50 > -100
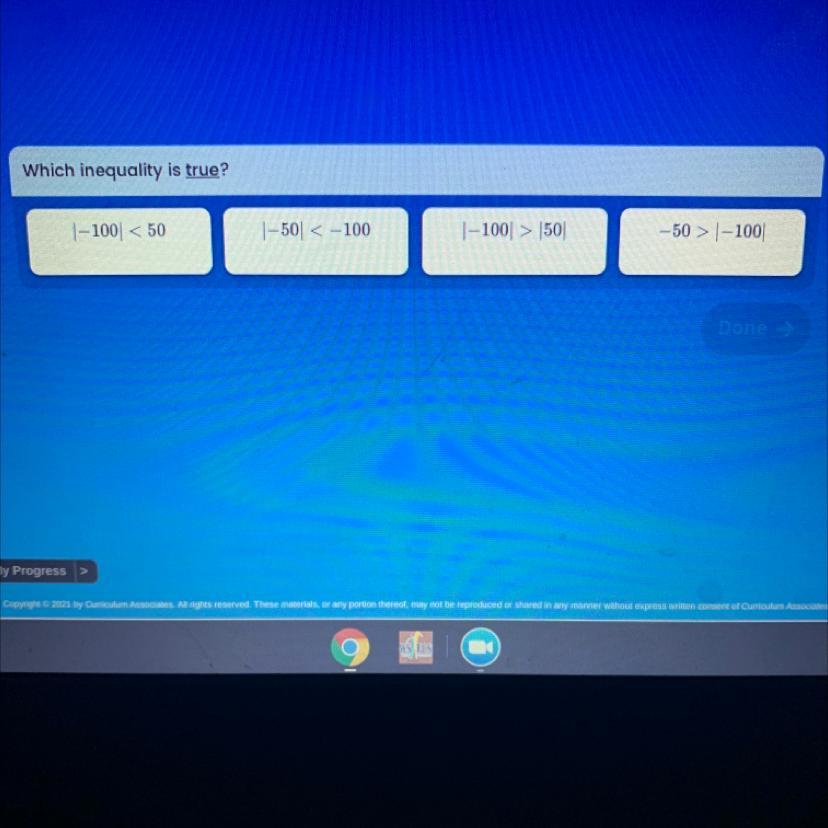
Answers
the third one, you have written not clearly
bwhwhsbsh hsbsvs bw wjw wjw whe
Consumers Energy states that the average electric bill across the state is $39.09. You want to test the claim that the average bill amount is actually different from $39.09. What are the appropriate hypotheses for this test
Answers
The null hypothesis is \(\mu = 39.09\)
The symbol \(\mu\) is the Greek letter mu
The alternate hypothesis is \(\mu \ne 39.09\) telling us we have a two-tailed test here. The "not equal" is directly tied to the keyword "different" given in the instructions. In other words, mu being different from 39.09 directly leads to \(\mu \ne 39.09\)
So either mu is 39.09 or it's not 39.09
You can use H0 and H1 to represent the null and alternate hypotheses respectively.
----------------------
Summary:
The two hypotheses are
H0: \(\mu = 39.09\)
H1: \(\mu \ne 39.09\)
This is a two tailed test.
John drove 138 miles in 3 hours. Use the formula d = rt, where d is distance, r is rate, and is time, to find John's rate of speed
in miles per hour.
Answers
By the formula d = rt, we obtain that the speed of John is 46 miles per hour.
What is a unitary method?A unitary method is a mathematical way of obtaining the value of a single unit and then deriving any no. of given units by multiplying it with the single unit.
Given, John drove 138 miles in 3 hours.
The speed of John can be obtained by dividing the total distance covered by the amount of time.
Also given, The formula to find John's rate of speed is, d = rt.
Therefore,
138 = 3r.
r = 138/3.
r = 46 miles per hour.
learn more about the unitary method here :
https://brainly.com/question/28276953
#SPJ1
The kettle in Keith,s kitchen is 80% full. After 20% of the water in it has been poured out. There are 1152ml of water left. What volume of water does Keith’s kitchen kettle hold when it is full?
Answers
The volume of water that Keith's kitchen kettle holds when it is full is 1800 ml.
Assume that Keith's kitchen kettle has a "x" ml capacity when it is full.
The kettle is initially 80% full, which means it holds 0.8x ml of water, according to the problem.
20% of the water is poured out, leaving 80% of the original amount of water in the kettle, which is:
0.8x * 0.8 = 0.64x ml
We are informed that the 1152 ml of water that is left equates to:
0.64x = 1152
By multiplying both sides by 0.64, we obtain:
x = 1800
Consequently, Keith's cooking kettle has an 1800 ml capacity when it is full.
To know more similar question visit:
https://brainly.com/question/79178
#SPJ1
Which shows how to calculate the number of liters he used if he used 5 cups of water?
divide 5 by 4.22
multiply 5 by 4.22
divide 5 by 1.05
multiply 5 by 1.05
Answers
Answer:
The first one is d) fluid ounces
The second one I think is c) meters
the third one I think is d) 2kg
Step-by-step explanation:
QUESTION ON PIC THANK YOU

Answers
Answer:
10/10
Step-by-step explanation:
Graphing rational functions. I need help asap!!!!

Answers
Answer:
1.
Vert. asymptote: x = {-3, 2}
Horiz. asymptote: y = 0
x-int: None
Question 3.
a. There is no hole
b. Vert. asymptote: x = {-2, 2}
c. f(x) = 0: x = {0, -1/2}
d. The graph has no hole at (-2, 4)
Question 4.
a. Vert. asymptote: x = {-2, 2}
b. f(x) = 0: x = {0, -1/2}
c. Horizontal asymptote: y = 2
d. The graph has no hole
I'm a bit confused. Some of the things stated in the question aren't true like how there are holes in places where there aren't.
11. Which of the following points is on the
line 3x - 5y = 1
A. (1, 2)
B. (2,1)
C. (3/5,1)
D. (2,3)
Answers
Answer:
B. (2,1)
Step-by-step explanation:
Substitute the first value from the parentheses for x, and the second value for y in the equation.
Calculate.
If the answer is true, the point is a solution on the line.
3(2) -5(1) = 1
6 –5 = 1
1 = 1. True. point B is a solution on the line.
D* for example:
3(2) -5(3) = 1
6 - 15 = 1
–9 = 1 False. This is not a solution on the line.
You get the idea. The others are also false.
Determine the minimum sample size needed if we want to estimate the population percent of students who LOVE statistics. We want the estimate to be within 5% of the true proportion, with 99% confidence. Assume a previous study estimated that percent to be twenty percent. 425 43 101 664
Answers
425 is the smallest sample size required when the percentage of pupils in the population who LOVE statistics.
Given that,
We have to find the smallest sample size required to determine the percentage of pupils in the population who LOVE statistics. With 99% confidence, the estimate should be within 5% of the true proportion. Assume that past research pegged that percentage at 20%.
p = 0.20
1 - p = 0.80
Margin of error = E = 0.05
At 99% confidence level
α= 1 - 99%
α = 1 - 0.99 =0.01
α/2 = 0.005
Zα/2 = Z0.005 = 2.576
Sample size = n = (Zα / 2 / E )2 × p × (1 - p)
= (2.576 / 0.05)2 × 0.20 × 0.80
= 424.68
Sample size = n = 425
Therefore, 425 is the smallest sample size required when the percentage of pupils in the population who LOVE statistics.
To learn more about size visit: https://brainly.com/question/18587054
#SPJ4
I would like help on this can you please help

Answers
Given:
A function
\(f(x)=-2x^2+9\)and value of g(x) at x.
To find:
Maximum value of both functions.
Explanation:
For criticle points find f'(x) = 0 and f''(x)>0. Then value will be maximum.
Solution:
Now, first derivative is
\(\begin{gathered} f^(x)=-2x^2+9 \\ f^{\prime}(x)=-4x \end{gathered}\)Now, put f'(x)=0 and criticle point will be 0.
Now,
\(f^{^^{\prime}^{\prime}}(x)=-4\)As second derivative of function is negetive at x=0. So, we will get maximum at x=0
So, At x=0
\(f(0)=9\)So, maximum value of f(x) is 9 and maximum value of g(x) is 11.
Hence, this is the maximum values of f(x) and g(x).
Find the average of the numbers 6 4/7, 1 5/56, 9 1/7, 3 5/8. Write the solution as a mixed number or a fraction in lowest terms.
Answers
Answer:
\(\frac{187}{112}\)
Step-by-step explanation:
Just add them all up in the calculator and divide by the number of numbers, which in this case is 4
Step-by-step explanation:
follow the steps in the attached
