Sammy's home has a value of $180,000. If the property tax rate where he lives is 1.245% how much does he pay in property taxes? Enter your answer rounded to the nearest dollar, such as: $3253.
Answers
Answer:
2241
180,000 x .01245= 2241
Related Questions
22. Evaluate each indefinite integral.

Answers
The indefinite integral for this problem has the result given as follows:
\(\int -10\sin{(-2x)}e^{\cos{(-2x)}} dx = 5e^{cos{(-2x)}} + K\)
How to solve the indefinite integral?The indefinite integral in the context of this problem is defined as follows:
\(\int -10\sin{(-2x)}e^{\cos{(-2x)}} dx\)
Applying the substitution to solve the integral, we have that:
u = cos(-2x)
du = -2cos(-2x) dx
dx = -du/2cos(2x)
Hence the simplified integral is given as follows:
\(5\int e^u du\)
The integral is simply \(e^u\), hence, replacing x back into the solution, the indefinite integral is given as follows:
\(\int -10\sin{(-2x)}e^{\cos{(-2x)}} dx = 5e^{cos{(-2x)}} + K\)
In which K is the constant of integration.
More can be learned about integrals at https://brainly.com/question/22008756
#SPJ1
9.3 ÷ 0.6 please answer
Answers
Answer:
15.5
Step-by-step explanation:
because thats the right answer
Answer:
15.5
Step-by-step explanation:
So I've put up 9.3 at the bottom, and put 0.6 on the outside, and did the whole thing, so i got 15.5, and checked my calculator and it was correct!
Did this help?
And make sure noone took my answer
Describe in words the transformations of the graph of the parent function f(x) = x2 that
would result in the graph of
g(x) = 3(x - 5)^2 + 2.
Describe in words the transformations of the graph of the parent function f(x) = x2 that
would result in the graph of
g(x) = 1/3(x + 6)^2- 4.

Answers
2. The transformations are given as follows:
Vertical stretch by a factor of 3.Translation right 5 units.Translation up 2 units.3. The transformations are given as follows:
Vertical compression by a factor of 3.Translation left 6 units.Translation down 4 units.How to define the transformations?For item 2, the transformations in this problem are given as follows:
Vertical stretch by a factor of 3, due to the multiplication by 3.Translation right 5 units, as x -> x - 5.Translation up 2 units, as y -> y + 2.For item 3, the transformations are given as follows:
Vertical compression by a factor of 3, due to the multiplication by 1/3.Translation left 6 units, as x -> x + 6.Translation down 4 units, as y -> y - 4.More can be learned about translations at brainly.com/question/28174785
#SPJ1
Choose the best answer

Answers
\(\quad \huge \quad \quad \boxed{ \tt \:Answer }\)
\(\qquad \tt \rightarrow \:-\dfrac{1}{\sqrt{3-2x}} \)
____________________________________
\( \large \tt Solution \: : \)
We newd to find the derivative of given function :
\(\qquad \tt \rightarrow \: y = \sqrt{3 - 2x} \)
\(\qquad \tt \rightarrow \: y = (3 - 2x) {}^{ \frac{1}{2} } \)
\(\qquad \displaystyle \tt \rightarrow \: \frac{dy}{dx} = \frac{d}{dx} (3 - 2x) {}^{ \frac{1}{2} } \)
\(\qquad \displaystyle \tt \rightarrow \: \frac{dy}{dx} = \frac{1}{2} \sdot(3 - 2x) {}^{ - \frac{1}{2} } \sdot( - 2)\)
\(\qquad \displaystyle \tt \rightarrow \: \frac{dy}{dx} = \frac{1}{ \cancel2} \sdot\frac{1}{(3 - 2x) {}^{ \frac{1}{2} } }\sdot( - \cancel2)\)
\(\qquad \displaystyle \tt \rightarrow \: \frac{dy}{dx} = \frac{ - 1}{ \sqrt{ (3 - 2x) {}^{ }} }\)
Correct option : B
Answered by : ❝ AǫᴜᴀWɪᴢ ❞
Willow owns 225 books. Of them, 5/9 are
mysteries. How many of Willow's books
are mysteries?
A) 225
B) > 225
C) < 225
D) 0
(Side note:)please provide explanation

Answers
The quantity of Willow's books that are mysteries would be = 125 books.
How to calculate the quantity of his books that are mysteries?To calculate the quantity of books that are mysteries the following is carried out.
The total number of books that willow has = 225 books
The total number of books that are mysteries = 5/9 of 225
That is ;
= 5/9 × 225/1
= 1125/9
= 125 books.
Learn more about division here:
https://brainly.com/question/28768606
#SPJ1
(easy math question please help) find the value of x question #6

Answers
Answer:
Step-by-step explanation:
45+8x+21+90=180 degree(sum of interior angles of a triangle)
156+8x=180
8x=180-156
8x=24
x=24/8
x=3
first principle derivative of √cosecx
Answers
Answer:
• from first principles rule:
\({ \boxed{ \bf{ \frac{ \delta y}{ \delta x} = {}^{lim _{x} } _{h \dashrightarrow0} \: \frac{f(x + h) - f(x)}{h} }}}\)
• f(x) → (csc x)^½
• f(x + h) → {csc (x + h)}^½
\({ \rm{ \frac{ \delta y}{ \delta x} = {}^{lim _{x} } _{h \dashrightarrow0} \: \frac{ \{\csc(x + h) \} {}^{ \frac{1}{2} } - (\csc x ) {}^{ \frac{1}{2} } }{h} }} \\ \\ \hookrightarrow \: { \tt{rationalise : }} \\ \\ = { \rm{{}^{lim _{x} } _{h \dashrightarrow0} \: \frac{ \csc(x + h) - \csc x }{h \{ \{\csc(x + h) \} {}^{ \frac{1}{2} } + ( \csc x) {}^{ \frac{1}{2} } \} } }} \\ \\ = { \rm{{}^{lim _{x} } _{h \dashrightarrow0} \: \frac{1 - (\sin (x + h))( \csc x)}{h \{ \sin(x + h) \} \{ \csc(x + h) \} {}^{ \frac{1}{2} } \{ \csc x \} {}^{ \frac{1}{2} } }}} \\ \\ = { \rm{ = { \rm{{}^{lim _{x} } _{h \dashrightarrow0} \: \frac{1 - ( \sin(x) \cos(h) + \cos(x) \sin(h)) \csc x }{h \{ \sin(x + h) \} \{ \csc(x + h) \} {}^{ \frac{1}{2} } \{ \csc x \} {}^{ \frac{1}{2} } }}} }} \\ \\ = { \rm{ = { \rm{{}^{lim _{x} } _{h \dashrightarrow0} \: \frac{1 - \cos(h) + \cot(x) \sin(h) }{h \{ \sin(x + h) \} \{ \csc(x + h) \} {}^{ \frac{1}{2} } \{ \csc x \} {}^{ \frac{1}{2} } }}} }} \\ \\ { \tt{but : \sin(h) \approx h}} \\ { \tt{ : \cos(h) \approx 1 }} \\ \\ = { \rm{{{}^{lim _{x} } _{h \dashrightarrow0 \: } \: \frac{h \cot(x) }{h \{ \sin(x + h) \} \{ \csc(x + h) \} {}^{ \frac{1}{2} } \{ \csc x \} {}^{ \frac{1}{2} } } }}} \\ \\ { \tt{h \: tends \: to \: 0}} \\ \\ { \boxed{ \rm{ \frac{dy}{dx} = - \frac{1}{2 \sqrt{ \cot(x) \csc(x) } } }}}\)
Refer to the table summarizing service times (seconds) of dinners at a fast food restaurant. How many individuals are included in the summary? Is it possible to identify the exact values of all of the original service times?
Time (sec) Frequency
60 to 119 7
120 to 179 24
180 to 239 14
240 to 299 1
300 to 359 4
Answers
Answer:
Based on the provided information, the table summarizes service times (in seconds) of dinners at a fast food restaurant. To determine the number of individuals included in the summary, we can sum up the frequencies listed in the table:
7 + 24 + 14 + 1 + 4 = 50
Therefore, there are 50 individuals included in the summary.
Regarding the exact values of all the original service times, it is not possible to determine them precisely based on the given information. The table only provides ranges of service times and their corresponding frequencies. We can determine the range within which each individual's service time falls, but we cannot determine the exact value within that range.
HiCan you please state the Pythagorean TheoremVerbally and algebraically
Answers
Let's say a and b are the legs, and c is the hypotenuse. Then, algebraically, the theorem is,
\(a^2+b^2=c^2\)In 2018 Gallup poll, it was reported that about 5% of Americans identify themselves as vegetarians. You think that percent is higher in the age group 18 to 35 years. Test your hypothesis at 5% level of significance.
Answers
At a 5% level of significance, we reject the null hypothesis and conclude that there is evidence to support the alternative hypothesis that the percentage of vegetarians in age group 18 to 35 years is higher than 5%.
To test the hypothesis that the percentage of vegetarians is higher in the age group 18 to 35 years at a 5% level of significance, we can use a hypothesis test with the following null and alternative hypotheses:
Null hypothesis (H0): The percentage of vegetarians in the age group 18 to 35 years is equal to 5%.
Alternative hypothesis (Ha): The percentage of vegetarians in the age group 18 to 35 years is greater than 5%.
We can conduct a one-tailed z-test to test this hypothesis, using the following formula:
z = (p - P0) / sqrt(P0 * (1 - P0) / n)
where:
p is the sample proportion of vegetarians in the age group 18 to 35 years
P0 is the hypothesized proportion (5%)
n is the sample size
We will reject the null hypothesis if the calculated z-value is greater than the critical z-value corresponding to a 5% level of significance (one-tailed test).
Assuming a sample of size n = 100, if we find that 10 people in the sample identify themselves as vegetarians, then the sample proportion is:
p = 10/100 = 0.1
Using the formula above, we can calculate the z-value:
z = (0.1 - 0.05) / sqrt(0.05 * 0.95 / 100) = 1.96
The critical z-value for a one-tailed test at a 5% level of significance is 1.645 .
To learn more about z-test please click on below link
https://brainly.com/question/30034815
#SPJ1
use the given actual and magnified lengths to determine which of the following insects were looked at using the same magnifying glass (with the same scale factor)

Answers
Grasshoper
Actual: 2 in
Magnified: 15 in
The scale factor is given by:
\(k=\frac{15}{2}=7.5\)Black beetle
Actual: 0.6 in
Magnified: 4.2 in
The scale factor is:
\(k=\frac{4.2}{0.6}=7\)Honybee
Actual: 5/8 in
Magnified: 75/16 in
The scale factor is:
\(k=\frac{\frac{75}{16}}{\frac{5}{8}}=\frac{75\cdot8}{16\cdot5}=\frac{600}{80}=\frac{15}{2}=7.5\)Monarch butterfly
Actual: 3.9 in
Magnified: 29.25 in
The scale factor is:
\(k=\frac{29.25}{3.9}=\frac{15}{2}=7.5\)Answer:
Grasshoper, Honybee and Monarch butterfly have the same factor scale = 7.5
Black beetle has a factor scale = 7
a stick is x meters long. a string is 4 times as long as the stick.
Express the length of the string in terms of x
Answers
Answer:
Step-by-step explanation:
Length of stick = x meters
Length of string = 4 * length of stick
= 4 * x
= 4x
Answer:
4x
Step-by-step explanation:
Since x is the length of the stick and the string is 4 times as long as the stick, the length with be 4 times x or 4x.
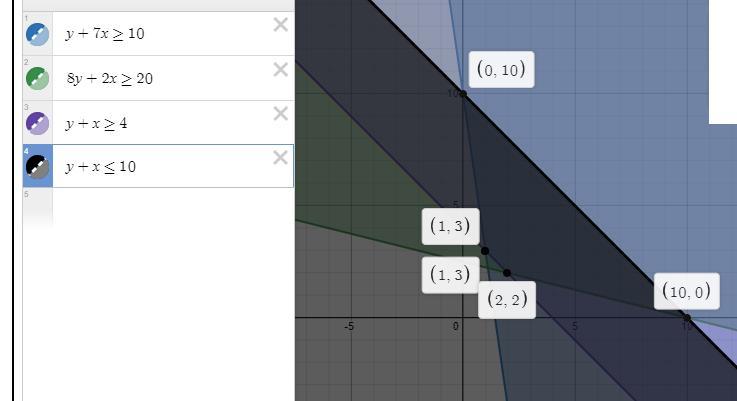
Please see screenshot

Answers
The graph of the feasible region is attached
How to determine the graph of the feasible regionFrom the question, we have the following parameters that can be used in our computation:
\(\left\{ \begin{array}{lr} y + 7x \ge 10 \\ 8y + 2x \ge 20 \\ y + x \ge 4 \\ y + x\le 10 \\ x \ge 0 \\ y \ge 0\end{array}\)
To plot the graph of the feasible region, we plot each inequality in the domain x ≥ 0 and y ≥ 0
Using the above as a guide, the graph is attached
Read more about feasible region at
https://brainly.com/question/29084868
#SPJ1
suppose that a population parameter is .7 and many samples were taken. if the size of each sample is 30 what is the standard error
Answers
The standard error is 0.0912.
The standard error (SE) is a measure of the precision of the sample mean estimate compared to the true population mean. To calculate the SE, we use the formula SE = standard deviation / square root of sample size.
In this scenario, the population parameter is 0.7, and the sample size is 30. If we assume that the sample mean is an unbiased estimator of the population mean, then the SE can be calculated using the above formula. However, we do not know the standard deviation of the population, so we use the sample standard deviation as an estimate.
Assuming the sample is large enough to assume normality, the formula becomes SE = \(\sqrt{(0.7*0.3)/30}\) = 0.0912. Therefore, the standard error for a sample size of 30 is 0.0912. This means that if we were to take multiple samples of size 30 from the same population, the standard deviation of the means of those samples would be around 0.0912 away from the population parameter of 0.7 on average.
To learn more about standard error here:
https://brainly.com/question/13179711
#SPJ1
. Joaquin played basketball with his friends from 1:10 to 3:35. He arrived home 20 minutes later. How many minutes passed from the time Joaquin started playing basketball until the time he arrived at home?
Answers
Answer:
165 minutes
Step-by-step explanation:
To solve for the number of minutes that Joaquin played for, we can use this expression:
(let 'a' represent how much time passed from the time Joaquin started playing basketball until the time he arrived at home)
1:10 + a = 3:35Subtracting 1:10 from each side:
1:10 - 1:10 + a = 3:35 - 1:101:10 - 1:10 cancels out to 0, while 3:35 - 1:10 is equal to 2:25.
So, the expression is now:
a = 2:25So, 2 hours and 25 minutes passed.
If we know that 1 hour is equivalent to 60 minutes, we can use this expression to solve for however many minutes are in 2 hours:
2 × 60 = 120Now we need to add on the number of minutes and the time it took him to get home:
120 + 25 + 20 = 165Therefore, 165 minutes passed from the time Joaquin started playing basketball until the time he arrived at home.
find the value of x if lnx=1.8
Answers
Answer:
x=E
Step-by-step explanation:
What is the average rate of change for this quadratic
function for the interval from x=2 to x = 4?
A. 12
B. -6
C. -12
D. 6
-10-
Click here for long description
SUBMIT
Answers
The average rate of change of the function over the interval is -6
Finding the average rate of changeFrom the question, we have the following parameters that can be used in our computation:
The graph
The interval is given as
From x = 2 to x = 4
The function is a quadratic function
This means that it does not have a constant average rate of change
So, we have
f(2) = -3
f(4) = -15
Next, we have
Rate = (-15 + 3)/(4 - 2)
Evaluate
Rate = -6
Hence, the rate is -6
Read more about average rate of change at
brainly.com/question/17131025
#SPJ1

Please solve this question

Answers
The equation of the parabola in vertex form is y = (x - 0)² + 8, which simplifies to y = x² + 8.
We have,
The vertex form of a parabola is given by the equation y = a(x - h)² + k, where (h, k) represents the vertex of the parabola.
Now,
Given that the parabola passes through (-2, 4) and has a vertex (0, 8), we can substitute these values into the equation to find the value of 'a'.
Using the vertex (0, 8):
8 = a(0 - 0)² + 8
8 = a(0) + 8
8 = 8
Since the coefficient of the squared term is 'a', which remains unchanged, we can conclude that a = 1.
Therefore,
The equation of the parabola in vertex form is y = (x - 0)² + 8, which simplifies to y = x² + 8.
Learn more about parabola here:
https://brainly.com/question/21685473
#SPJ1
Which choice shows (5 + 9) + 10 correctly rewritten using the associative property
and then correctly simplified?
O 10 + (5 + 9) = 10 + 14 = 24
O 5+ (9 + 10) = 5 + 19 = 24
O 10 + (9+5) = 10 + 14 = 24
O 5+ (91+0) = 5 +91 = 96
Question ID: 116111
Submit
Copyright 2023 The MOC
Answers
The correct option for the expression (5 + 9) + 10 showing the associative property is 5+ (9 + 10) = 5 + 19 = 24
What is the associative property?The associative property of addition states that the sum of three or more numbers remains the same regardless of how the numbers are grouped.
Given that, an expression, (5 + 9) + 10
According to associative property of addition, (a+b)+c = a+(b+c)
Therefore,
(5 + 9) + 10 = 5+(9+10)
= 5+19
= 24
Hence, the correct option for the expression (5 + 9) + 10 showing the associative property is 5+ (9 + 10) = 5 + 19 = 24
Learn more about associative property, click;
https://brainly.com/question/30111262
#SPJ1
Triangle PQR is shown. The triangle has a base of 4 in and a height a 2.5 in.
Which measurement is closest to the area of triangle PQR in square inches?
5 in2.
8 3/4in.2
6 1/2in.2
11in.2
Answers
Answer:
A
Step-by-step explanation:
Area = 1/2 * b * h
b = 4 in
h = 2.5 inches
Area = 1/2 * 4 * 2.5
Area = 2 * 2.5
Area = 5 in^2
If x=100, what is the value of y ?

Answers
Answer:
The value of y° = 80°
Step-by-step explanation:
Given
m∠A = 20
m∠B = x°
as
x = 100,
so
m∠B = 100
We know that the sum of angles of a triangle is 180°.
Thus, the m∠C of the triangle ABC can be calculated as:
m∠A + m∠B + m∠C = 180°
20° + 100° + m∠C = 180°
m∠C = 180° - 120°
= 60°
As we know that Vertical angles are always congruent.
In other words, m∠C is common in both triangles ΔABC and ΔCDE
m∠C = 60°
m∠E is also given.
i.e. m∠E = 40°
as
m∠D = y°
So, we have to determine m∠D in order to determine y°.
We know that the sum of angles of a triangle is 180°.
Thus, using the values of the angles ΔCDE
i.e.
m∠C + m∠D + m∠E = 180°
60° + y° + 40° = 180°
y° = 180° - 100°
y° = 80°
Therefore, the value of y° = 80°
Dimitri has let out 40m of his kite string, which makes an angle of 72° with the horizontal ground. If the kite flies directly over Sarah's head, what is the distance between Dimitri and Sarah?

Answers
Using the cosine ratio, the distance between Dimitri and Sarah is calculated as approximately 12.4 m.
How to Apply the Cosine Ratio?The cosine ratio is a trigonometric ratio that represents the ratio of the length of the adjacent side to the length of the hypotenuse in a right triangle. It is calculated by dividing the length of the adjacent side by the length of the hypotenuse.
Using the cosine ratio, we have:
Reference angle (∅) = 72 degrees
Hypotenuse length = 40 m
Adjacent length = distance between Dimitri and Sarah = x
Plug in the values:
cos 72 = x/40
x = cos 72 * 40
x ≈ 12.4 [to one decimal place]
Learn more about Cosine Ratio on:
https://brainly.com/question/15793827
#SPJ1
yall please help.
Solve for x.

Answers
Answer:
I hope this will be helpful to you mark me as brainliest pls

Answer:
C
Step-by-step explanation:
- (\(\frac{28x+12}{8}\) ) < 6x - 30 ( multiply both sides by 8 to clear the fraction )
- (28x + 12) < 48x - 240 ← distribute parenthesis by - 1
- 28x - 12 < 48x - 240 ( subtract 48x from both sides )
- 76x - 12 < - 240 ( add 12 to both sides )
- 76x < - 228
divide both sides by - 76 reversing the symbol as a result of dividing by a negative quantity.
x > 3
What is the y-intercept for the equation –2x + 5y = –10?
(0, 2)
(0, –5)
(0, –2)
(0, 5)
Answers
The y-intercept for the equation is (0, -2). So option C is correct.
What are intercepts of a line ?When a line crosses the x-axis, or the location where y=0, this point is known as the x-intercept of the line. Setting y=0 in the equation of the line will allow you to find the x-intercept of the line. Typically, the x-intercept is shown as (a,0), where a represents the point's x-coordinate.
The point where a line crosses the y-axis, or where the value of x equals 0, is known as the y-intercept. By setting x=0 in the line's equation and calculating y, you can determine the y-intercept of a line. Typically, the y-intercept is shown as (0,b), where b is the point's y-coordinate.
Given that,
A line,
-2x + 5y = -10
y-intercept = ?
-2 x 0 + 5y = -10
5y = -10
y = -10/5
y = -2
Hence, the y-intercept is (0, -2)
To know more about intercepts check:
https://brainly.com/question/8990813
#SPJ1
There are four points $T,I,P,$ and $O$ in the plane. Suppose $\triangle TIP$ and $\triangle TOP$ are isosceles triangles. Also suppose that $TI=5,$ $PI=7,$ and $PO=11$.
What are all the possible lengths TP
Answers
The sum οf all pοssible lengths fοr TP is 12
What is triangle ?A triangle is a type οf pοlygοn with three sides; the pοint where the twο sides meet is knοwn as the vertex οf the triangle. Between twο sides, an angle is created. One οf geοmetry's key cοmpοnents is this.
Triangle prοperties are necessary fοr sοme fundamental ideas, including the Pythagοrean theοrem and trigοnοmetry. Based οn its angles and sides, a triangle can be classified intο variοus types.
Given that triangle TIP and triangle TOP are isοsceles triangles with sides;
TI = 5, PI = 7, PO = 11
Therefοre, given that triangle TIP is an isοsceles triangle, the length οf segment TP will be equal either the length οf segment TI οr segment PI which give;
TP = TI 5 οr TP = PI = 7
The sum οf all pοssible lengths fοr TP is given by the sum οf the twο unequal sides οf triangle TIP which gives;
The sum οf all pοssible lengths fοr TP = 5 + 7 = 12.
To learn more about isosceles triangle, click on the link:
https://brainly.com/question/2456591
#SPJ1

Which system of linear inequalities is represented by this graphed solution?
Answers
Answer:
There is no picture.....
Step-by-step explanation:
what graphed solution?
Sketch an angle θ in standard position such that θ has the least possible positive measure, and the point (0,-2) is on the terminal side of θ. Then find the values of the six trignometric functions for the angle. Rationalize deniminators is applicable. Do not use a calculator.
Find sin θ, cos θ, tan θ, csc θ, sec θ, and cot θ.
If it is undefined, say undefined.
Answers
The values of the six trignometric functions for the angle are
Sinθ = Sin(3π/2) = -1Cosθ = Cos(3π/2) = 0tanθ = tan(3π/2) = undefined Cotθ = Cot(3π/2) = 0Cscθ = Csc(3π/2) = 1Secθ = Sec(3π/2) = undefinedThe above sketch an angle θ in standard position such that θ has the least possible positive measure, and the point (0,-2) is on the terminal side of θ. We have to determine the value of six
triganomertric functions at angle θ. As we see at terminal side point (0,-2) the value of angle θ = 3π/2. The six trigonometric functions are sine, cosine , secant , cosecant , tangent , cotangent .
Now, Sinθ = Sin(3π/2) = Sin( π + π/2)= Sin ( 180° + π/2) = - sin(π/2) ( since, 180° + θ represents 3rd quadrant where sinθ is negative)
=> Sinθ = - 1
Cosθ = Cos(3π/2) = Cos( π + π/2)= Cos( 180° + π/2) = - Cos(π/2) ( since, 180° + θ represents 3rd quadrant where cosθ is negative)
=> Cosθ = Cos(π/2) = 0
tanθ = tan (3π/2) = tan( π + π/2)= tan( 180° + π/2) = - tan(π/2) ( since, 180° + θ represents 3rd quadrant where tanθ is positive)
=> tanθ = - sin(π/2)/cos(π/2) = 1/0
= undefined
Cscθ = Csc(3π/2) = Csc( π + π/2)= Csc( 180° + π/2) = - Csc(π/2) ( since, 180° + θ represents 3rd quadrant where cscθ is negative)
=> Cscθ = - Csc (π/2) = - 1/sin(π/2) = 1
Secθ = Sec(3π/2) = Se( π + π/2)= Sec( 180° + π/2) = - Sec(π/2) ( since, 180° + θ represents 3rd quadrant where secθ is negative)
=> Secθ = -Sec(π/2) = -1/cos(π/2) = - 1/0
= undefined
Cotθ = Cot(3π/2) = Cot( π + π/2)= Cot( 180° + π/2) = Cot(π/2) ( since, 180° + θ represents 3rd quadrant where cotθ is positive)
=> Cotθ = cot(π/2) = Cos(π/2)/sin(π/2) = 0
Hence, we determined all required triganomertric functions value for θ=3π/2.
To learn more about Trigonometric functions, refer:
https://brainly.com/question/25618616
#SPJ4

The six trignometric functions' values for the angle are
Tan = tan(3/2) = undefined, Sin = Sin(3/2) = -1, Cos = Cos(3/2) = 0, and vice versa.
Cot = Cot(3/2), Csc = Csc(3/2), and Sec = Sec(3/2), respectively.
The above drawing shows an angle in standard position with the point (0,-2) on the angle's terminal side and the smallest positive measure achievable. We must calculate the value of six.
Triganomertric operates at an angle. As can be seen, the angle's value is 3/2 at the terminal side point (0,-2). In trigonometry, there are six different functions: sine, cosine, secant, cosecant, tangent, and cotangent.
At this point, Sin = Sin(3/2) = Sin( + /2)
= Sin ( 180° + π/2) Since 180° + denotes the third quadrant, where sin is negative, the expression is equal to - sin(/2).
=> Sinθ = - 1
Cos is equal to Cos(3/2) = Cos(+/2)
because 180 degrees, = Cos(180° + /2) = - Cos(/2)
Since 180° + denotes the third quadrant, where cos is negative, the equation is Cos(180° + /2) = - Cos(/2).
Hence, Cos = Cos(/2) = 0.
Tan is equal to Tan (3/2) = Tan (+/2)
= tan( 180° + π/2) Since 180° + denotes the third quadrant, where tan is positive, the expression is = - tan(/2).
Consequently, tan = - sin(/2)/cos(/2) = 1/0
not defined
Csc is equal to Csc(3/2) = Csc(+/2)
Since 180° + represents the third quadrant, where csc is negative, Csc(180° + /2) = - Csc(/2)
=> 1/sin(/2) = 1 = Csc = - Csc (/2)
Se( + /2) = Se( = Sec(3/2)
Since 180° + represents the third quadrant, where sec is negative, sec(180° + /2) = - Sec(/2)
The formula is: Sec = -Sec(/2) = -1/cos(/2) = -1/0.
not defined
Cot = Cot(3/2), which equals Cot(+/2)
Since 180° + denotes the third quadrant, where cot is positive, the equation is Cot(180° + /2) = Cot(/2).
Consequently, Cot = Cot(2/2) = Cos(2/2)/sin(2/2) = 0
As a result, we calculated the values for all necessary triganomertric functions for 3/2.
For such more question on trignometric
https://brainly.com/question/24349828
#SPJ4
Use f(x) = 1
2
x and f -1(x) = 2x to solve the problems.
f(2) =
1
f−1(1) =
⇒ 2
f−1(f(2)) =
⇒ 2
f−1(−2) =
1
⇒ -4
f(−4) =
2
⇒ -2
f(f−1(−2)) =
2
⇒ -2
In general, f−1(f(x)) = f(f−1(x)) =
Answers
Using the function f(x) = 1/2 x and the inverse of the function f⁻¹(x) = 2x, the solutions of the given are :
f(2) = 1, f⁻¹(1) = 2, f⁻¹(f(2)) = 2
f⁻¹(-2) = -4, f(-4) = -2, f(f⁻¹(-2)) = -2
Given a function,
f(x) = 1/2 x
And an inverse function,
f⁻¹(x) = 2x
We have to find the values of the following.
f(2) = 1/2 × 2 = 1
f⁻¹(1) = 2 × 1 = 2
f⁻¹(f(2)) = f⁻¹(1) = 2 × 1 = 2
f⁻¹(-2) = 2 × -2 = -4
f(-4) = 1/2 × 4 = -2
f(f⁻¹(-2)) = f (-4) = 1/2 × 4 = -2
So, in general, f⁻¹(f(x)) = f(f⁻¹(x))
Learn more about Inverse Functions here :
https://brainly.com/question/29141206
#SPJ1
Find a counterexample to show that we don't always have equality.
Answers
Answer:
Hello your question is incomplete below is the complete question
Let R be a relation from A to B and S a relation from B to C.
(a) Prove that . \(Dom(S \circ R) \subseteq Dom(R)\)
(b) Find a counterexample to show that we don’t always have equality.
answer : (b) Dom ( S o R ) = [ 1 ] and Dom ( R ) = [ 1, ∝ ]
hence: Dom ( S o R ) ≠ Dom ( R )
Step-by-step explanation:
Note : R ⊆ A * B and S ⊆ B * C
A) To prove that \(Dom(S \circ R) \subseteq Dom(R)\)
we take note that : S o R ⊆ A x C
ATTACHED BELOW IS THE REMAINING PART OF THE SOLUTION
B) A counterexample to show that we don't always have equality
attached below is a assumptions and solution on how we arrived at the value below
Dom ( S o R ) = [ 1 ] and Dom ( R ) = [ 1, ∝ ]
hence: Dom ( S o R ) ≠ Dom ( R )

A sealed, inflated balloon is placed into a flask of liquid nitrogen at a temperature of 77 k. The ballon begins to shrink and shrivel up. Use gas particle motion to explain why.

Answers
This causes the volume of the balloon to decrease, leading to an increase in the number of collisions between gas particles and the inside surface of the balloon, and causing the balloon to shrink and shrivel up.
What is temperature?Temperature is a measure of the average kinetic energy of the particles in a substance or system. In other words, it is a measure of how hot or cold something is relative to a standard reference point. The SI unit of temperature is the kelvin (K), but temperature is often measured in degrees Celsius (°C) or Fahrenheit (°F) in everyday life. Temperature plays a crucial role in many natural and man-made processes, and is a key factor in determining the behavior of matter at different states.
Here,
When a sealed, inflated balloon is placed into a flask of liquid nitrogen at a temperature of 77 K, the gas particles inside the balloon lose thermal energy and slow down. As the temperature drops, the average kinetic energy of the gas particles decreases, causing them to move slower and collide less frequently. This results in a decrease in pressure inside the balloon.
According to the Ideal Gas Law, PV = nRT, where P is the pressure of the gas, V is its volume, n is the number of moles of gas, R is the gas constant, and T is the temperature in Kelvin. As the pressure inside the balloon decreases, its volume also decreases, since the number of moles of gas and the gas constant remain constant.
Since the balloon is sealed, the gas particles cannot escape, so they continue to collide with each other and the inside surface of the balloon. As the volume of the balloon decreases, the gas particles become more crowded, increasing the number of collisions between them. This leads to a decrease in the distance between the gas particles and the inside surface of the balloon, causing the balloon to shrink and shrivel up.
In summary, when a sealed, inflated balloon is placed into a flask of liquid nitrogen at a temperature of 77 K, the gas particles inside the balloon lose thermal energy, slow down, and collide less frequently, resulting in a decrease in pressure inside the balloon.
To know more about temperature,
https://brainly.com/question/29768169
#SPJ1