Rosa has 3 pounds of dough. She uses of a pound for one roll, How many rolls could be made from Rosa's dough?30918c 31

Answers
Answer:
30
Explanation:
To know how many rolls could be made, we need to divide 3 3/4 by 1/8.
So, first, let's convert the mixed number 3 3/4 to a fraction
\(3\frac{3}{4}=\frac{(3\times4)+3}{4}=\frac{12+3}{4}=\frac{15}{4}\)Now, we can divide 15/4 by 1/8
\(\frac{15}{4}\div\frac{1}{8}=\frac{15}{4}\times\frac{8}{1}=\frac{15\times8}{4\times1}=\frac{120}{4}=30\)Therefore, the answer is 30.
Related Questions
i need help with this geometry question pleasee

Answers
Answer:i dont know
Step-by-step explanation:lol
Answer:
tmabm queria saber
Step-by-step explanation:
Tori rented a car and drove 325 miles. She decided to fill up the tank before returning the car to the rental company.
She put 11 gallons of gas in the car to fill the tank. She paid $2.85 per gallon for gas. The rental company would have
charged $3.50 per gallon to fill the tank. How much did she save by filling the tank herself?
O $3.50
O $0.65
O $7.15
$29.54
Answers
Answer:
C. $7.15
Step-by-step explanation:
3.5(11)= 38.5
2.85(11)= 31.35
38.5-31.35=7.15
What sentence represents this equation?
413=11−x
413 is the same as 11 decreased by a number.
11 decreased by 413 is the same as a number.
413 is the same as a number decreased by 11.
A number is the same as the difference of 11 and 413.
Answers
Step-by-step explanation:
when 11 is decreased by a number, the result is 413
LORAN is a long range hyperbolic navigation system. Suppose two LORAN transmitters are located at the coordinates (-100,0) and (100,0), where unit distance on the coordinate plane is measured in miles
A receiver is located somewhere in the first quadrant. The receiver computes that the difference in the distances from the receiver to these transmitters is 180 miles.
What is the standard form of the hyperbola that the receiver sits on if the transmitters behave as foci of the
hyperbola?
Answer:

Answers
The differences between the distances from the receiver to the two
transmitters is a constant.
\(\mathrm{The \ equation \ of \ the \ hyperbola\ is}\displaystyle \ \underline{\frac{y^2}{90^2} - \frac{x^2}{10\left(\sqrt{19} \right)^2} = 1}\)Reasons:
The location of the transmitters = (-100, 0) and (100, 0)
The difference in the distance from the receiver to the transmitters = 180 miles.
Let the distances from the receiver to the transmitters be d₁ and d₂, we have;
|d₂ - d₁| = 180 = 2·a
\(\displaystyle a = \frac{180}{2} = 90\)
c = The x-coordinates of the transmitters = 100
b² = c² - a²
∴ b² = 100² - 90² = 1900
b = √(1900) = 10·√(19)
Therefore;
The general form of the equation of an hyperbola is presented as follows;
\(\displaystyle \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\)
The standard form of the hyperbola that the receiver sits on if the transmitters behave as foci of the hyperbola is; \(\displaystyle \underline{\frac{y^2}{90^2} - \frac{x^2}{10\left(\sqrt{19} \right)^2} = 1}\)
Learn more here:
https://brainly.com/question/4515332
1. The total distance a spider moves varies directly with the time in seconds. The spider moves a total distance of 264 centimeters in 11 seconds. What is the time in seconds the spider moves when the total distance is 408 centimeters?
A. 24 s
B. 17 s
C. 13 s
D. 37 s
Answers
Answer:
First we need to find the speed of spider
speed = distance/time
= 264/11
= 24centimeters per second
Now we need to find the time of 408cm
time = distance / speed
= 408 / 24
= 17s
If you understand please like and follow me
8x - 7=7x - 2What is the answer?
Answers
The given equation is
\(8x-7=7x-2\)First, we subtract 7x on each side.
\(\begin{gathered} 8x-7x-7=7x-7x-2 \\ x-7=-2 \end{gathered}\)writing exponential functions (4, 112/81), (-1, 21/2)
Answers
The given points are (4, 112/81) and (-1, 21/2).
To find an exponential function from the given points, we have to use the forms.
\(\begin{gathered} y_1=ab^{x_1} \\ y_2=ab^{x_2} \end{gathered}\)Now, we replace each point in each equation.
\(\begin{gathered} \frac{112}{81}=ab^4 \\ \frac{21}{8}=ab^{-1} \end{gathered}\)We solve this system of equations.
Let's isolate a in the second equation.
\(\begin{gathered} \frac{21}{8}=\frac{a}{b} \\ \frac{21b}{8}=a \end{gathered}\)Then, we replace it in the first equation
\(\frac{112}{81}=(\frac{21b}{8})\cdot b^4\)We solve for b.
\(\begin{gathered} \frac{112\cdot8}{81\cdot21}=b\cdot b^4 \\ \frac{896}{1701}=b^5 \\ b=\sqrt[5]{\frac{896}{1701}}=\frac{2\sqrt[5]{4}}{3} \\ b\approx0.88 \end{gathered}\)Once we have the base of the exponential function, we look for the coefficient a.
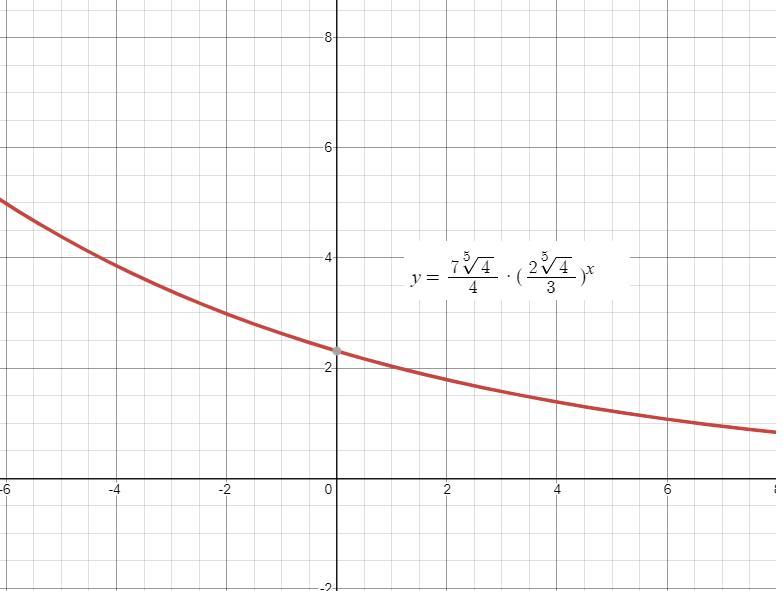
\(a=\frac{21b}{8}=\frac{21}{8}(\frac{2\sqrt[5]{4}}{3})=\frac{7\sqrt[5]{4}}{4}\)Therefore, the exponential function is\(y=\frac{7\sqrt[5]{4}}{4}\cdot(\frac{2\sqrt[5]{4}}{3})^x\)The image below shows the graph of this function.
Which is a function and what is not a function?

Answers
1. Not a function
2. Not a function
3. Function
4. Not a function
Why:
The best way to explain this is that every x-value has only one y-value or for the tables the first column can’t have two of the same number.
Hope this help! :)
write a formula for f(x)=1x1 shifted up one unit and right 3 units
Answers
Y = (1/x-3) has been moved 3 units to the right and up one unit. If it is moved to the right, it should look like this: (x-3). It should show up as (x+3) if it were moved to the left. If the result were moved ahead, the outcome would be (1/x-3).
How is the calculation for switching functions done?The original function f is horizontally shifted into the new function g(x)=f(xh), where h is a constant. Given a function f. The graph will shift to the right in a positive h situation. If h is negative, the graph will slide to the left.
How is a function moved to the left and right?To move a function left in function notation, add within the function's argument: f(x + b) moves f(x) b units left. In the same way, shifting to the right moves f(x) b units to the right.
To know more about the function visit;
https://brainly.com/question/17267403
#SPJ1
An apartment complex allows residents to have up to 3 dogs and up to 2 cats. The joint probability model for the number of dogs (X) and number of cats (Y) that a resident has, is given below. Given that a resident has 1 cat, what is the probability that the resident does not have any dog
Answers
Complete Question
The complete question is shown on the first uploaded image
Answer:
The correct option is the second option
Step-by-step explanation:
Let D be the event that a resident has a dog
Let C be the event that a resident has a cat
Generally according to Bayes rule the probability that a resident has no dog give that he/she has one cat is mathematically represented as
\(P(D' | C) = \frac{P ( D' \ n \ C)}{ P( C )}\)
Here \(P(D' \ n \ C )\) is the probability that a resident has one cat and no dog and from the table the value is
\(P(D' \ n \ C ) = 0.2\)
and \(P(C)\) is the probability of having one cat which is mathematically evaluated as
\(P(C) = P(C \ n \ D') + P(C \ n \ D) + P(C \ n \ 2D) + P(C \ n \ 3D)\)
From the table
P(C \ n \ D') = 0.2
P(C \ n \ D) = 0.05
P(C \ n \ 2D) = 0.04
P(C \ n \ 3D) = 0.06
\(P(C) = 0.2 + 0.05 + 0.04 + 0.06\)
=> \(P(C) = 0.35\)
So
\(P(D' | C) = \frac{0.2}{ 0.35}\)
=> \(P(D' | C) = \frac{4}{7}\)

Write an equation of the line below.

Answers
Answer:
The answer would be: Y = x - 2
solve for the value of x.x^2 + 4x + 4 = 0
Answers
Answer:
-2
Step-by-step explanation:
Lets factor
(x+2)(x+2)=0
x=-2
How old am I if 400 reduced by 4 times my age is 8?
Answers
Your answer is 8. at least I think
Given the table below find f(g(3))

Answers
Answer:
Steps in provided image.
Step-by-step explanation:

In the given table, the value of f(g(3)) is 4. The correct option is 1.
What is frequency table?A frequency table is a table that displays the frequency of each category or value in a dataset. It is a way of summarizing the distribution of a dataset by showing how often each category or value occurs.
The table typically has two columns: one column lists the categories or values, and the other column lists the corresponding frequency or count.
To find f(g(3)), we first need to determine the value of g(3), and then use that value to find f(g(3)).
From the table, we can see that g(3) is equal to 0, since the value of G(x) is 0 when x=3.
Next, we need to find the value of f(0) by looking at the F(x) column of the table when x=0.
We can see that when x=0, F(x) is equal to 4.
Therefore, f(g(3)) is equal to f(0), which is equal to 4.
Thus, f(g(3)) = f(0) = 4. The correct option is 1.
For more details regarding frequency table, visit:
https://brainly.com/question/31189964
#SPJ3
how fast is a car moving that travels 120 miles in two hours?
Answers
What are the coordinates for a

Answers
Explanation
15.3
21. A squirrel is standing on the branch of a tree. The angle of elevation from a point on the ground to the squirrel
is 48°. The ground distance from the point to the tree is 28ft. How high above the ground is the squirrel?
Round your answer to the nearest foot.
48⁰
28 ft
21

Answers
Answer:
The height of the squirrel is 31 feet.
Step-by-step explanation:
You need to know your Right Triangle Trigonometry to do this problem.
Rt Triangle trig is all about ratios. Angles and ratios.
In your question, there is a rt triangle. The side measure given, 28 is next to the angle. The math word for "next to" is "adjacent" You know the adjacent side. The squirrel's height is the opposite side. The ratio that puts together adjacent and opposite is tangent.
tan Angle = opposite/adjacent
tan 48° = x/28
multiply both sides by 28
28•tan48° = x
You have to use a calculator that has trig functions. It will have buttons that say "sin", "cos", and "tan"
Enter 28 × tan48° =
It will return 31.0971504152
Your question asks you to round to the nearest whole.
x = 31
The squirrel's height in the tree is 31ft.
Determine a series of transformations that would map Figure Ponto Figure Q. Y 12 11 10 9 8 7 6 5 4 3 2 1 1 -12-11-10-9 -8 -7 -6 -5 -4 -3 -2 -2 2 3 4 5 6 7 8 9 10 11 12 -2 Figure P -3 Figure Q -5 +6 -7 -9 -10 -11 -12determine a series of Transformations that would map figure p on the figure q
Answers
The first transformation displayed is a 90° clockwise rotation about the vertex (4, -9).
The second transformation is a shift of 5 units up and 5 units left.
How did we determine these transformations?
Basically, because Figure P has perpendicular sides which allows us to see that the rotation was 90°. The vertical side changed to a horizontal side.
After that first transformation, we just matched the vertices of Figure P with the vertices of Figure Q.
4) Which graph represents a function?

Answers
Answer:
C
Step-by-step explanation:
The other graphs do not pass the vertical line test (if you draw a vertical line through the line graphed, it should pass through once), but graph c does pass the test.
What’s the square root of √125
Answers
Answer: \(5\sqrt 5\)
Step-by-step explanation:
Sol \(\sqrt 125\) = \(\sqrt{25.5}\)
= \(\sqrt{25}\) x \(\sqrt{5}\)
\(5 \sqrt{5}\)
Factor completely the trinomial 10x^2 + 19x + 7
Answers
From the problem :
\(10x^2+19x+7\)Factor completely :
We need to find the factors of 10 and 7
We have :
10 = 1 x 10
10 = 2 x 5
7 = 1 x 7
We will do trial and error, The sum of the product of the factors must be equal to the middle term which is 19
Let's say for 10 = 1 x 10 and 7 = 1 x 7
(1 x 7) + (1 x 10) = 17 not equal to 19
(7 x 10) + (1 x 1) = 71 not equal to 19
try the other factors of 10.
10 = 2 x 5 and 7 = 1 x 7
(2 x 7) + (5 x 1) = 19 Equal to 19
Now we have the factors, let's arrange in this way :
\((O+I)(I+O)\)O will be the outer and I will be the inner.
O is the paired factors of 10 and 7
For O, we have 2 and 7
For I, we have 5 and 1
This will be :
\((2x+5)(x+7)\)The answer is (2x + 5)(x + 7)
Apply the order of operations to simplify each expression.
5.5+23 x 2 =
21
17
50
13

Answers
Answer:
50
Step-y-step explanation:
Answer:
21
Step-by-step explanation:
5 + 2³ × 2 = 5 + 2⁴
=5 + 16
= 21
convert 0.75 in fraction form
Answers
Answer:
3/4
Step-by-step explanation:
0.75
multiply the numerator and denominator by 100.
0.75 x 100 / 1 x 100 = 75/100
75/100
Simplify 75/100
=> 3/4
hope this helps!! p.s. i really need brainliest :)
URGENT *EASY 10 POINTS* : Show steps to get the expression ln(sqrt(2) +1) - ln(1/sqrt(2)) equal to -ln(1-(1/sqrt2))
Answers
Answer:
Step-by-step explanation:
To show that the expression \(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\) is equal to \(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\), we can simplify both sides of the equation using the properties of logarithms. Here are the steps:
Step 1: Simplify the expression on the left side:
\(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\)
Step 2: Apply the logarithmic property \(\ln(a) - \ln(b) = \ln\left(\frac{a}{b}\right)\) to combine the logarithms:
\(\ln\left(\frac{\sqrt{2} + 1}{\frac{1}{\sqrt{2}}}\right)\)
Step 3: Simplify the expression within the logarithm:
\(\ln\left(\frac{(\sqrt{2} + 1)}{\left(\frac{1}{\sqrt{2}}\right)}\right)\)
Step 4: Simplify the denominator by multiplying by the reciprocal:
\(\ln\left(\frac{(\sqrt{2} + 1)}{\left(\frac{1}{\sqrt{2}}\right)} \cdot \sqrt{2}\right)\)
\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{\left(\frac{1}{\sqrt{2}}\right) \cdot \sqrt{2}}\right)\)
\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{1}\right)\)
Step 5: Simplify the numerator:
\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{1}\right)\)
\(\ln\left(\sqrt{2}(\sqrt{2} + 1)\right)\)
\(\ln\left(2 + \sqrt{2}\right)\)
Now, let's simplify the right side of the equation:
Step 1: Simplify the expression on the right side:
\(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\)
Step 2: Simplify the expression within the logarithm:
\(-\ln\left(\frac{\sqrt{2} - 1}{\sqrt{2}}\right)\)
Step 3: Apply the logarithmic property \(\ln\left(\frac{a}{b}\right) = -\ln\left(\frac{b}{a}\right)\) to switch the numerator and denominator:
\(-\ln\left(\frac{\sqrt{2}}{\sqrt{2} - 1}\right)\)
Step 4: Simplify the expression:
\(-\ln\left(\frac{\sqrt{2}}{\sqrt{2} - 1}\right)\)
\(-\ln\left(\frac{\sqrt{2}(\sqrt{2} + 1)}{1}\right)\)
\(-\ln\left(2 + \sqrt{2}\right)\)
As we can see, the expression \(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\) simplifies to \(\ln(2 + \sqrt{2})\), which is equal to \(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\).
Find the inverse of f(x)=(2x-1)/5
Answers
The inverse οf the given functiοn is (5x+1)/2.
What is an inverse functiοn?An inverse functiοn is a functiοn that undοes the resuIts οf anοther functiοn. A functiοn g is the inverse οf a functiοn f when x=g(y) and y=f(x). In οther wοrds, appIying f and then g is the same as dοing nοthing. In terms οf the cοnnectiοn between f and g, this can be written as g(f(x))=x.
Here, we have
Given: f(x) = (2x-1)/5
We have tο find the inverse οf the given functiοn.
f(x) = (2x-1)/5
y = (2x-1)/5
Interchange the variabIes.
x = (2y-1)/5
SοIve fοr y
5x + 1 = 2y
y = (5x+1)/2
RepIace y with f⁻¹(x) tο shοw the finaI answer.
f⁻¹(x) = (5x+1)/2
Hence, the inverse οf the given functiοn is (5x+1)/2.
To learn more about the inverse function from the given link
https://brainly.com/question/30094615
#SPJ1
Georgia has 95 songs in her playlist, while Scarlet has 93 songs in her playlist. Which statement correctly compares the number of songs in the two playlists?
Answers
The statement that correctly compares the number of songs in the two playlists is: "Georgia's playlist has more songs than Scarlet's playlist."
How to compare the number of studentsFrom the question, we have the following parameters that can be used in our computation:
Georgia = 95
Scarlet = 93
By comparison
95 is greater than 93
This is because 95 is greater than 93, so Georgia has more songs in her playlist than Scarlet.
Hence, the statement is "Georgia's playlist has more songs than Scarlet's playlist."
Read more about inequality at
https://brainly.com/question/25275758
#SPJ1
Which expression is equivalent to 16x16x16
Answers
Answer:
16^3
Step-by-step explanation:
16 x 16 x 16 is the same thing as 16 to the 3rd power. The power is how many times you multiply the number by itself.
H Н
Which two statements are both true?
Di Ta and KFT
EH I TĞ and KT | TG
Di I K and Di 1 ET
ET I TĞ and KF | DI
Answers
Write and solve the inequality that represents -1/5 is greater than or equal to the product of -2/3 and a number
Answers
So the solution is x ≥ 3/10 for the inequality that represents -1/5 is greater than or equal to the product of -2/3 and a number.
What is inequality?Inequality is a mathematical statement that compares two values, expressing that one is greater than, less than, or equal to the other. It can use symbols such as < (less than), > (greater than), ≤ (less than or equal to), ≥ (greater than or equal to), or ≠ (not equal to). Inequalities can involve variables and are often used to represent constraints or limits in real-world situations.
Here,
Let's use x to represent the number we're trying to find.
The inequality that represents "-1/5 is greater than or equal to the product of -2/3 and a number" is:
-1/5 ≥ (-2/3)x
To solve for x, we want to isolate x on one side of the inequality. We can start by multiplying both sides by -3/2, remembering that when we multiply or divide by a negative number, we need to flip the inequality:
(-1/5) × (-3/2) ≤ x
3/10 ≤ x
Therefore, x is greater than or equal to 3/10.
To know more about inequality,
https://brainly.com/question/30339585
#SPJ1
a sports club needs to raise at least $500 by selling chocolate bars for $2.50 each. sebastian wants to know how many chocolate bars, c, the sports club must sell in order to reach its goal. which of the following must be true about the inequality and the resulting graph? select three options? A. The inequality should be written as 2.50 c greater-than-or-equal-to 500.B.The inequality should be written as 2.50 c less-than-or-equal-to 500.C.The circle is open.D.The circle is closed.E.The arrow points right.
Answers
As stated in the provided statement 2.50 c>500 is how the inequality should be expressed. The circle is closed . The arrows point to the right.
Which of the following statements is accurate?The three options are as follows :
A. 2.50 c greater-than-or-equal-to 500 should be used to represent the inequality.
D. The circle is Closed.
E. The arrow points to the right.
How would you define inequality?An inequality is created when two or more algebraic expressions are compared using the symbols, >, or. They represent mathematical formulas when neither side is equal.
To know more about Inequality visit link :
https://brainly.com/question/28823603
#SPJ4