Rewrite the equation below so that it does not have fractions.
4-(3)/(4)x=(5)/(6)
Do not use decimals in your answer. PLS HELPPP
Answers
Answer:
9x=38
Step-by-step explanation:
Related Questions
A company currently has 200 units of a product on-hand that it orders every two weeks (14 days) when the salesperson visits the premises. Demand for the product averages 20 units per day with a standard deviation of 5 units. Lead time for the product to arrive is seven days. Management has a goal of a 95 percent probability of not stocking out for this product. The salesperson is due to come in late this afternoon when 180 units are left in stock (assuming that 20 are sold today). How many units should be ordered?
Answers
To determine the number of units that should be ordered, we need to consider the lead time, demand, and the desired probability of not stocking out.
1. First, let's calculate the demand during the lead time. Since the lead time is 7 days and the average daily demand is 20 units, the demand during the lead time is 7 days * 20 units/day = 140 units.
2. Next, we calculate the safety stock needed to achieve the 95% probability of not stocking out. The safety stock is the product of the standard deviation and the Z-score corresponding to the desired service level. For a 95% probability, the Z-score is 1.65. So, the safety stock is 1.65 * 5 units = 8.25 units (rounding up to 9 units).
3. Now, we calculate the reorder point, which is the sum of the demand during the lead time and the safety stock. Reorder point = 140 units + 9 units = 149 units.
4. Finally, we subtract the current on-hand units and the units sold today from the reorder point to determine the number of units to be ordered. Units to be ordered = 149 units - 180 units + 20 units = -11 units.
Since we cannot order a negative number of units, we conclude that no units should be ordered in this scenario.
Based on the given information and calculations, no units should be ordered in this case as there is no need to replenish the stock.
To know more about probability , visit ;
https://brainly.com/question/30884104
#SPJ11
jasmine's swimming lesson lasts 2-3 of an hour it takes 1-6 of an hour to do her homework does jasmine's spend more time on her home work or her swimming lesson PLEASE HELP DUE TODAY IN I READY MATH BOOK
Answers
Answer:
spends more time on swimming
Find 34−13.95 . Express your answer in decimal form.
Answers
Answer:
34-13.95 = 20.05
Step-by-step explanation:
Answer:
20.05
Step-by-step explanation:
34 - 13.95 = 20.05
An expert witness for a paternity lawsuit testifies that the length of a pregnancy is normally distributed with a mean of 280 days and a standard deviation of 13 days. An alleged father was out of the country from 240 to 306 days before the birth of the child, so the pregnancy would have been less than 240 days or more than 306 days long if he was the father. The birth was uncomplicated, and the child needed no medical intervention. What is the probability that he was NOT the father? What is the probability that he could be the father? Calculate the z-scores first, and then use those to calculate the probability.
Answers
For an a normally distributed the length of a pregnancy, with mean of 280 days and a standard deviation of 13 days,
a) the probability that he was NOT the father is equals to the 0.9762.
b) The probability that he could be the father is equals the 0.0238.
We have an expert witness for a paternity lawsuit testifies that the length of a pregnancy is normally distributed. Let variable X has normal distribution, Mean, μ = 280 days
standard deviations, σ = 13 days
An alleged father was out of the country from 240 to 306 days before the birth of the child. So, the variable value varies X < 240 or X> 306. Using Z-Score formula for normal distribution,
\(z= \frac{x -μ}{σ}\)
For x = 240
=> z =( 240 - 280)/13
= -40/13 = - 3.07
For x = 306
=> z = (306 - 280)/13
= 26/13 = 2
a) Probability that he not be the father , P ( 240< x < 306) or P(E)
= \( P ( \frac{240 - 280}{13 }< \frac{x - \mu}{\sigma} < \frac{306 - 280}{13})\)
= P (- 3.07 < z < 2 )
= P( x< 2) - P(z< - 3.07)
Using the normal distribution table value of probabilities for z < 2 and z< - 3.07 are determined, = 0.9762
= P(240<x <306)
b) Probability that he could be the father,
\(P( \bar E) \) = 1 - P(E)
= 1 - 0.9762
= 0.0238
Hence, required value is 0.0238.
For more information about normal distribution, visit :
https://brainly.com/question/4079902
#SPJ4
Determine the equation of the tangent plane and normal line of
the curve f(x,y,z)=x2+y2-2xy-x+3y-z-4 at p(2,
-3, 18)
Answers
To determine the equation of the tangent plane and normal line of the given curve at the point P(2, -3, 18), we need to find the partial derivatives of the function f(x, y, z) = x^2 + y^2 - 2xy - x + 3y - z - 4.
Taking the partial derivatives with respect to x, y, and z, we have:
fx = 2x - 2y - 1
fy = -2x + 2y + 3
fz = -1
Evaluating these partial derivatives at the point P(2, -3, 18), we find:
fx(2, -3, 18) = 2(2) - 2(-3) - 1 = 9
fy(2, -3, 18) = -2(2) + 2(-3) + 3 = -7
fz(2, -3, 18) = -1
The equation of the tangent plane at P is given by:
9(x - 2) - 7(y + 3) - 1(z - 18) = 0
Simplifying the equation, we get:
9x - 7y - z - 3 = 0
To find the equation of the normal line, we use the direction ratios from the coefficients of x, y, and z in the tangent plane equation. The direction ratios are (9, -7, -1).Therefore, the equation of the normal line passing through P(2, -3, 18) is:
x = 2 + 9t
y = -3 - 7t
z = 18 - t
where t is a parameter representing the distance along the normal line from the point P.
To learn more about tangent plane click here : brainly.com/question/33052311
#SPJ11
Which algebraic expression represents the phrase “two times the quantity of a number minus 12”?
2y - 12
2(y -12)
2(y + 12)
2y + 12
Answers
Answer:
A
Step-by-step explanation:
two times a quantity of number_ 2y
minus twelve-. 2y - 12
Answer: A
Step-by-step explanation:
when my age is divided by 7 the remainder is 4, if your age is 3 times my age so when you divide your age by 7, what will be the remainder?
Answers
Answer:
12
Step-by-step explanation:
let my age be x
x/7=4cross multiplyyou will get 28so 3 times of 28 divided by 784 divided by 7 is 12Find the best linear approximation, L(x), to f(x) = e' near x = 0. i.L(x) = x+1 ii. L(x) = x iii. LX) = c + 1
Answers
The best linear approximation to the function f(x) = e^x near x = 0 is L(x) = x + 1.
The given function is f(x) = e^x near x = 0.
To find the best linear approximation, L(x), we use the formula:
L(x) = f(a) + f'(a)(x-a),
where a is the point near which we are approximating.
Let a = 0, so that a is near the point x = 0.
f(a) = f(0) = e^0 = 1
f'(x) = d/dx (e^x) = e^x;
so f'(a) = f'(0) = e^0 = 1
Substituting these values into the formula: L(x) = 1 + 1(x-0) = x + 1
Therefore, the best linear approximation to f(x) = e^x near x = 0 is L(x) = x + 1.
For instance, linear approximation is used to approximate the change in a physical quantity due to a small change in another quantity that affects it.
To know more about linear approximation, visit:
https://brainly.com/question/1621850
#SPJ11
The cost of 1 pear is 2 cents more than the cost of 1 apple.
Find the value of a and the value of p
Answers
If the value of apple = x
The value of pear = x + 2 cents
How do I find the area between two curves?
Answers
Finding the area between two curves involves finding the bounds of integration, taking the difference of the two functions, and finally integrating the resulting function to find the area enclosed by the two curves.
To find the area between two curves, you need to find the bounds of the integration, which are the points where the two curves intersect. Then you need to integrate the difference of the two functions using definite integration.
To perform the definite integration, you need to find the antiderivative (indefinite integral) of each function and then subtract the lower bound antiderivative from the upper bound antiderivative.
Here you can learn more about the area between two curves
https://brainly.com/question/25546169#
#SPJ11
Select all the equations where b=11b=11b, equals, 11 is a solution. Choose 2 answers: Choose 2 answers: (Choice A) A 2b=2112b=2112, b, equals, 211 (Choice B) B b+18=7b+18=7b, plus, 18, equals, 7 (Choice C) C 77=7b77=7b77, equals, 7, b (Choice D) D 9=b-29=b−29, equals, b, minus, 2 (Choice E) E 11=33\div{b}11=33÷b
Answers
Answer:
Step-by-step explanation:
We are to choose all the equation that evaluates b to be 11. The following equations are true;
77 = 7b
To get b, we will divide both sides by 7
77/7 = 7b/7
11 = b
b = 11
This shows that the equation is correct since b = 11
Also 9 = b-2
To get b, we will add 2 to both sides of the expression
9+2 = b-2+2
11 = b
b = 11
This shows that the equation is correct since b = 11
Hence option C and D are correct
Answer:
C and D
Step-by-step explanation:
You do the opposite of the question to get answer.
can someone pls help

Answers
Answer:
x=5
Step-by-step explanation:
An isosceles trapezoid has two pairs of congruent base angles. This means angle F has to equal angle E. So we have 2x^2+21=3x^2-4. Move the variables to one side and we get 25=x^2. Square root both sides and we get two values x=5 and x=-5. Since angles cannot necessarily be negative, we only want the positive value. In this case x=5.
find the equation of the plane with the given description in scalar form. passes through (1,−1,2) and is parallel to 11x+ 9y+ 6z=19.
Answers
The equation of the plane in the scalar form that passes through (1, -1, 2) and is parallel to 11x + 9y + 6z = 19 is
11x + 9y + 6z - 14 = 0.
We have,
The given plane, 11x + 9y + 6z = 19, can be rewritten as:
11x + 9y + 6z - 19 = 0.
where the actual form is ax + by + cz - d = 0
Now,
The coefficients of a, b, and c, namely 11, 9, and 6, represent the normal vector to the plane.
So, the normal vector to the desired plane is (11, 9, 6).
The required plane is parallel to the given plane.
Using the point-normal form of a plane equation, the equation of the desired plane can be written as:
11(x - 1) + 9(y + 1) + 6(z - 2) = 0.
where (1, -1, 2) is the point that passes through it.
Expanding and simplifying the equation,
11x - 11 + 9y + 9 + 6z - 12 = 0.
11x + 9y + 6z - 14 = 0.
Therefore,
The equation of the plane in scalar form that passes through (1, -1, 2) and is parallel to 11x + 9y + 6z = 19 is
11x + 9y + 6z - 14 = 0.
Learn more about the equation of a plane here:
https://brainly.com/question/17013160
#SPJ12
Find the value of x:

Answers
Answer:
x = 17°
Step-by-step explanation:
2x - 4= 30° {being vertically opposite angles }
2x = 30° + 4°
2x = 34°
x = 17°
Hope it will help :)
Find the independent and dependent variable in the following word problem: " Students at the Norwood High School homecoming dance always get their pictures taken. The number of pictures the photographer will take is determined by how many students are attending the dance.
Answers
Answer:
Step-by-step explanation:
....................................................
slader The logarithmic equation is a nonlinear regression equation of the form ya. The accompanying data are the shoe sizes and heights (in inches) of men. Graphs of the regression line and the logarithmic equation are also provided. Which equation is a better model for the data? Explain.
Answers
Answer:
The graphs and the table is missing in the question.
Step-by-step explanation:
The guidelines for interpreting correlation co-efficient r are :
1. Strong correlation 0.7<|r|≤1
2. Moderate correlation 0.4<|r|<0.7
3. Weak correlation 0.2<|r|<0.4
4. No correlation 0≤|r|<0.2
Logarithmic regression
(i). Mean : \($ {\overset{-}{ln}x} = \frac{\sum ln x_i}{n}, \ \ \ {\overset{-}y} = \frac{\sum y_i}{n} $\)
(ii) Trend line : \($ y = A +B \ln x, \ \ B = \frac{S_{xy}}{S_{xx}}, \ \ A={\overset{-}y-B{\overset{-}{\ln x}}}$\)
(iii). Correlation coefficient : \($ r = \frac {S_{xy}}{\sqrt{S_{xx}} \sqrt{S_{yy}}} $\)
\($ S_{xx} = \sum (\ln x_i - {\overset{-}{\ln x}})^2 = \sum (\ln x_i)^2-n. ({\overset{-}{\ln x}})^2$\)
\($ S_{yy} = \sum(y_i - {\overset{-}y})^2 = \sumy_i^2 - n. {\overset{-}y^2}$\)
\($ S_{xy} = \sum(\ln x_i - {\overset{-}{\ln x}})(y_i-{\overset{-}y}) = \sum \ln x_i y_i - n. {\overset{-}{\ln x}}{\overset{-}y} $\)
Now using the technology we can calculate
The equation of the regression curve is y = A + B(lnx)
we get A = 30.72 , B = 17.19
The equation of regression curve is \($ \hat y$\) = 30.72 + 17.19(lnx)
a rectangular warehouse will have 5000 square feet of floor space and will be separated into two rectangular rooms by an interior wall. the cost of the exterior walls is $140 per linear foot and the cost of the interior wall is $110 per linear foot. find the dimensions that will minimize the cost of building the warehouse.
Answers
x = 58.62 feet
y = 85.3 feet
Given that,
The cost of exterior walls is $140 per linear foot.
The cost of interior walls is $100 per linear foot.
xy = 5000
⇒ y = 5000/x
For the exterior walls, we have 2(x + y)(110)
For the interior wall, we have 100x
The cost function = C
⇒ C = 2(x + y)(110) + 100x
⇒ C = 220(x + y) + 100x
= 220x + 240y + 100x
= 320x + 240y
Recall that y = 5000/x
C = 320x + 220(5000/x)
C = 320x + 1100000/x
Differentiate C with respect to x
C'(x) = 320 - 1100000/x²
= (320x² -1100000) / x²
To minimize cost
C'(x) = 0
(320x² -1100000) / x² = 0
320x² -1100000 = 0
⇒ 320x² = 1100000
⇒ x² = 1100000/320
⇒ x = √1100000/320
⇒ x = 58.62 feet
Recall that y = 5000/x
y = 5000/58.62
y = 85.3 feet
Learn more about minimize:
https://brainly.com/question/13014022
#SPJ4
a raise of $310,000 is evenly distributed among 210 professors. estimate the amount each professor receives.
Answers
Each professor would receive an estimated amount of approximately $1,476.19.
the total number or quantity : aggregate. trying to figure the amount of time it will take. : the quantity at hand or under consideration.
To estimate the amount each professor receives, we divide the total raise of $310,000 by the number of professors, which is 210.
Amount each professor receives = Total raise / Number of professors
= $310,000 / 210
Using a calculator or performing the division, we find:
Amount each professor receives ≈ $1,476.19
Know more about amount here:
https://brainly.com/question/32453941
#SPJ11
whitch inequality represents this situation

Answers
Option B is correct, the inequality which represents the length of segment AB is greater than length of segment AD is 9x-16>1.5x+42
The given rectangle is ABCD.
The length of segment AB is 9x-16 units
The length of segment AD is 1.5x+42 units
We have to find the inequality which represents the length of segment AB is greater than length of segment AD
> is the symbol used to represent greater than
AB>AD
9x-16>1.5x+42
Hence, option B is correct, the inequality which represents the length of segment AB is greater than length of segment AD is 9x-16>1.5x+42
To learn more on Inequality click:
https://brainly.com/question/28823603
#SPJ1
A member only speaker series allows people to join for 6$ and then pay 4$ for every event attended .What is the maximum number of events someone can attend for a total cost of 50$
Answers
Answer:
11
Step-by-step explanation:
50-6=44
44/4=11
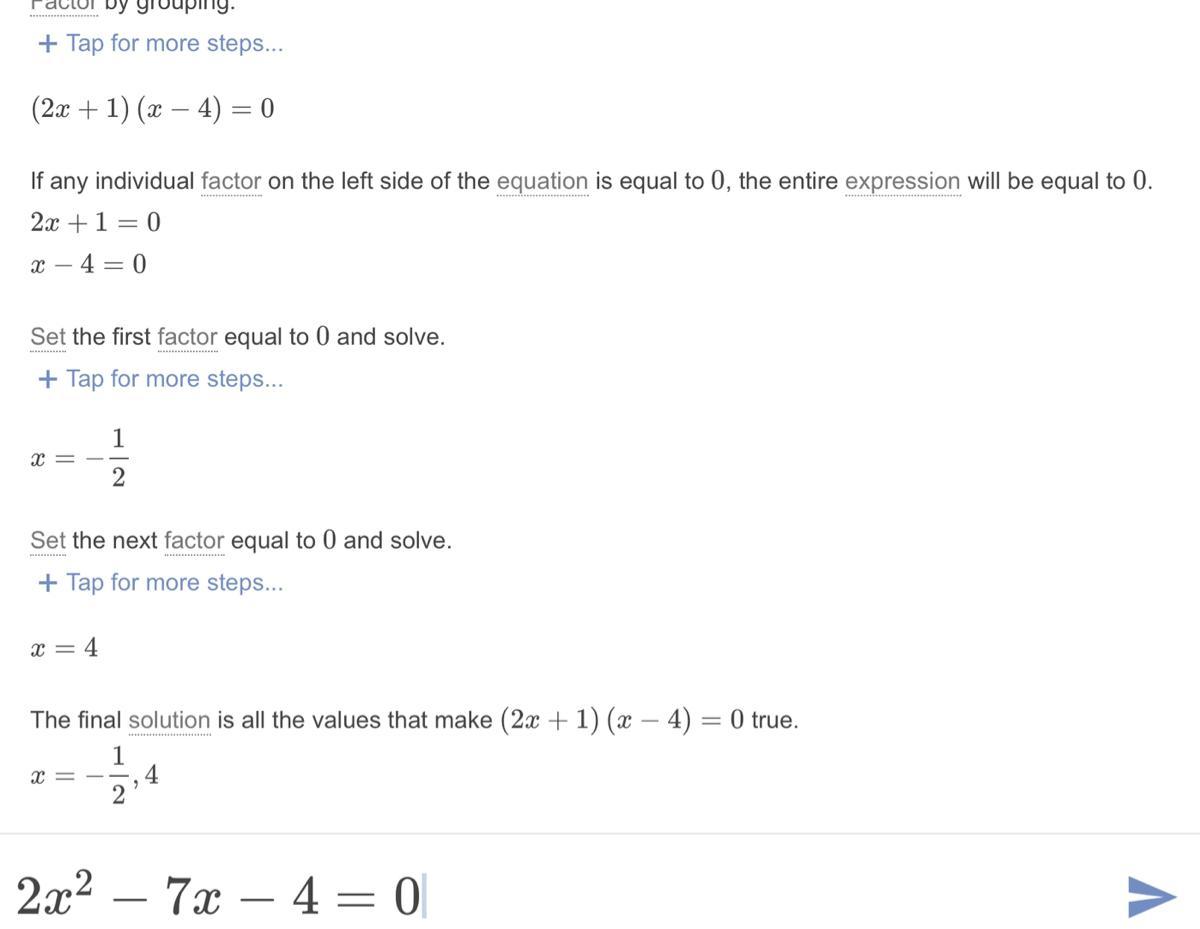
Solve by factoring 2x^2-7x-4=0
Answers
I have to write 20 words so here they are
Please help me with edge question .

Answers
\(~\hspace{7em}\textit{negative exponents} \\\\ a^{-n} \implies \cfrac{1}{a^n} ~\hspace{4.5em} a^n\implies \cfrac{1}{a^{-n}} ~\hspace{4.5em} \cfrac{a^n}{a^m}\implies a^na^{-m}\implies a^{n-m} \\\\[-0.35em] ~\dotfill\\\\ (4)^{\frac{-4}{2}} \implies (4)^{-2}\implies 4^{-2}\implies \cfrac{1}{4^2}\implies \cfrac{1}{16}\)
Just #9 please I need help (30 points)

Answers
Answer:
Step-by-step explanation:
The graph starts at x = - 3 and ends x = 2. For all x between -3 and 2, there points on the graph. Hence the domain, in interval notation, is written as
[-3 , 2]
We have closed circles at x = - 3 and x = 2 because -3 and 2 are included in the domain which is indicated by the closed brackets at x = - 3 and x = 2.
The range is the set of possible output values, which are shown on the y-axis.
This is why our graph goes from (-3,8) to (2,3)

What type of triangle is △str? right triangle equilateral triangle isosceles triangle scalene triangle
Answers
The type of triangle is △STR is isosceles triangle.
What's triangleA triangle is a flat shape bounded by three sides. In another sense, a triangle is formed by three line segments called sides and each side intersects with two other sides.
When classified from its angles, triangles consist of acute triangles, right triangles, and obtuse triangles. Even so, the sum of the angles of a triangle is always 180 degrees. Based on the classification of its sides, triangles consist of equilateral triangles, arbitrary triangles, and acute triangles.
Learn more about isosceles triangle at
https://brainly.com/question/2456591
#SPJ1

Find the distance between the points (7,9) and (6, 3).
Answers
Answer:
6.082763
Step-by-step explanation:
bubba decides to put an extra coat of paint on his barn. he buys 3 gallons of paint. the paint is applied with a thickness of 0.0552 mm. a gallon is the same as 3.78 liters volume. how large of an area cam bubba paint with a single coating of this paint if he manages a uniform thickness?
Answers
Bubba can paint an area of approximately 205,797.10 square meters with a single coating of the 3 gallons of paint, assuming he manages a uniform thickness.
The area that Bubba can paint with a single coating of the 3 gallons of paint, we need to first convert the volume of the paint into liters. As given, 1 gallon is the same as 3.78 liters.
3 gallons x 3.78 liters/gallon = 11.34 liters
Now, we need to use the thickness of the paint to calculate the area that can be covered with this amount of paint. The thickness of the paint is given as 0.0552 mm. We need to convert this to meters so that it is in the same units as the area. 1 mm is equal to 0.001 meters, so:
0.0552 mm x 0.001 meters/mm = 0.0000552 meters
The thickness of the paint in meters. Now we can use the volume and thickness of the paint to calculate the area that can be covered. The formula for this is:
Area = Volume / Thickness
Area = 11.34 liters / 0.0000552 meters
Area = 205,797.10 square meters
Yo know more about area visit:-
https://brainly.com/question/1631786
#SPJ11
The cost, in dollars, for a video game developer to code g games can be represented by the function v(g) . The number of games produced in w weeks is given by the function g(w) = 4w.
Answers
After w weeks, the expression for the total cost of games is 250 + 4000w.
What is Expression?
Mathematical expressions consist of at least two numbers or variables, at least one arithmetic operation, and a statement. It's possible to multiply, divide, add, or subtract with this mathematical operation. An expression's structure is as follows: Expression: (Math Operator, Number/Variable, Math Operator)
An algebraic expression known as a linear expression has terms that are either constants or variables raised to the first power. Alternatively put, none of the exponents can be greater than 1.
As an illustration, while x is a variable raised to the first power, x2 is a variable raised to the second power. An illustration of a constant is 5.
Linear expressions are what the two expressions are. One variable raised to the power of one makes up a linear expression.
250 + 1000g.
Where: g(w) = 4w.
250 + 1000(4w).
250 + 4000w.
Therefore, number of games produced in w weeks is 250 + 4000w.
Learn more about mathematical expression click here;
https://brainly.com/question/4344214
#SPJ4
let me know if you need to see the answer choices1) is, or is not 2) -3/2 and 3/4, -3/2 and 2/3, or -4/3 and 3/4 3) are, or are not

Answers
Quadrilateral ABCD is not a rectangle because consecutive sides have slopes of 3/4 and -3/2 so they are not perpendicular
1) Considering that to be a rectangle that quadrilateral needs to have perpendicular line segments and two pairs of congruent segments.
2) Let's find the slope of the line segments AB and BC, bearing in mind the coordinates of A(-2,-1) B(2,2) and C(4,-1)
\(\begin{gathered} m_{AB}=\frac{2-(-1)}{2-(-2)}=\frac{3}{4} \\ m_{BC}=\frac{-1-2}{4-2}=\frac{-3}{2} \\ m_{CD}=\frac{-4-(-1)}{0-4}=\frac{-3}{-4}=\frac{3}{4} \\ m_{AD}=\frac{-4-(-1)}{0-(-2)}=\frac{-3}{2} \end{gathered}\)Note, that in order to state that there are perpendicular lines, the slope of AB and BC should be the opposite and reciprocal so AB is 3/4 and BC should be -4/3. The same does not occur to AB and AD.
3) Hence, the answer is:
Quadrilateral ABCD is not a rectangle because consecutive sides have slopes of 3/4 and -3/2 so they are not perpendicular
Answer to this pls....

Answers
Answer:
\(\angle 1=32^{o}\)
Step-by-step explanation:
\(\angle 2 = 32^{o}, (corresponding-angles- are- equal)\\\angle 2=\angle 1, (alternate-angles - are-equal)\\therefore\\\angle 1=32^{o}\)
Describe how the graph is related to the graph of y = lxl.

Answers
Answer:
The graph is 1 unit shift to right of y = lxl
Step-by-step explanation:
horizontal shift to right 1 unit of y = lxl
