Researcher are recording how much of an experimental medication is in a person’s bloodstream every hour. they discover that half-life of the medication is about 6 hours.
Answers
When researchers record how much of an experimental medication is in a person's bloodstream every hour, they are measuring the medication's concentration over time. This information is important because it can help determine the medication's effectiveness and potential side effects.
The half-life of a medication is the time it takes for half of the drug to be eliminated from the body. In this case, the half-life of the experimental medication is about 6 hours.
Knowing the half-life of a medication is important because it can help predict how long it will take for the drug to be eliminated from the body and when the next dose should be administered. For example, if a medication has a half-life of 6 hours, it means that after 6 hours, half of the medication will be eliminated from the body.
After another 6 hours, half of the remaining medication will be eliminated, and so on.
By monitoring the concentration of the medication in a person's bloodstream every hour, researchers can determine how quickly the drug is being absorbed and eliminated from the body. z
This information can help optimize dosing and minimize potential side effects. Overall, understanding the pharmacokinetics of a medication is crucial for safe and effective use in clinical practice.
To know more about medication refer here
https://brainly.in/question/3845606#
#SPJ11
Related Questions
Answer the two questions below please

Answers
Answer:
Step-by-step explanation:
we can replace 5 with \(\sqrt{5}^{2}\)
then.
\(\sqrt{5}^{n-1+2}=\sqrt{5}^{n+1}\)
10.2.4:Using the bijection rule to count ternary strings whose digits sum to a multiple of 3. i About Let T={0,1,2}.A string x E T" is said to be balanced if the sum of the digits is an integer multiple of 3 (a) Show a bijection between the set of strings in T that are balanced and T.Explain why your function is a bijection (b) How many strings in T are balanced? Feedback?
Answers
There are 3 balanced strings in set T.
How many balanced strings are in set T?To count the number of balanced strings in the set T={0, 1, 2}, we can establish a bijection between the set of balanced strings and T itself. A balanced string is defined as a string in which the sum of its digits is a multiple of 3.
We can define a function f: T" -> T that maps each string in T" to T by preserving the balanced property. If a string in T" is already balanced, f returns the string itself. If the string is not balanced, f replaces the last digit with digit that makes the sum a multiple of 3.
By showing that this function is both injective (one-to-one) and surjective (onto), we establish a bijection. The bijection rule states that if two sets have a bijection between them, they have the same cardinality. Therefore, the number of balanced strings is equal to the number of elements in T, which is 3.
learn more about function
brainly.com/question/30721594
#SPJ11
Identify Central Ideas Explain how a country with little land and few natural resources could make up for such deficits-without depending on other countries-and have a healthy economy .
Answers
A country with little land and few natural resources could make up for such deficits without depending on other countries and having a healthy economy by developing its Human Capital.
What are examples of small countries with low natural resources and high GDP?Examples of small countries with low natural resources and high GDP are:
JapanVatican CityCosta Rica etc.It is to be noted that of all the factors of production, (Land, labor, Capital, and Entrepreneurship) Human Capital (Labor and Entrepreneurship) are the most valuable and yield the greatest return on investment.
The Democratic Republic of the Congo is commonly regarded as the world's richest country in terms of natural resources; its undiscovered stockpiles of raw minerals are estimated to be worth more than US $24 trillion.
Learn more about natural resources:
https://brainly.com/question/13954163
#SPJ1
Explain each step and write each expression as a product
(a+b)^2-(b+c)^2
Answers
a(a+2b) - c(c + 2b) is the product form of the expression (a+b)^2-(b+c)^2
How to simplify the expression as a productWhat is simplification of an algebraic expression?
Simplification of an algebraic expression is defined as a way of writing an expression in the most efficient and compact form without affecting the value of the original expression
Given (a+b)^2-(b+c)^2
(a+b)²-(b+c)² = (a+b)(a+b) - (b+c)(b+c) (Clear the parenthesis)
= ( a(a+b) + b(a+b) ) - ( b(b+c) + c(b+c) )
= (a² + ab + ab + b²) - (b²+ bc + bc +c²)
= (a² + 2ab + b²) - (b²+ 2bc +c²)
= a² + 2ab + b² - b² - 2bc - c² (Add/subtract like terms)
= a² + 2ab - 2bc - c² (Factorise)
= a(a+2b) - c(2b + c) (Rearrange)
= a(a+2b) - c(c + 2b)
Therefore, the expression (a+b)^2-(b+c)^2 can be simplified as a product to a(a+2b) - c(c + 2b)
Learn more about simplification of algebraic expression on:
https://brainly.com/question/723406
#SPJ1
I really need help with part a and b, please help. Incorrect answers will be downvoted, correct answers will be upvoted. 1. The army is interested in characterizing the acoustic signature of a helicopter. The following data show measurements of acoustic pressure (made dimensionless) for a two-bladed helicopter rotor through of a rotor revolution. The data points are equally spaced in time, and the period of the data collection is of a second. p=00.00040.0015 0.0028 0.0040 0.0048 0.0057 0.0071 0.0095 0.0134 0.0185 0.02420.0302 0.0364 0.0447 0.0577 0.0776 0.0955 0.0907 -0.0477 -0.0812 -0.0563 -0.0329 -0.0127 0.0032 0.0147 0.0221 0.0256 0.0255 0.0222 0.0170 0.0112 0.0064 0.0035 0.0023 0.0020 0.0019 0.0016 0.0009 0.0002 a) Find the real discrete Fourier transform for this data set. (b) Any term in the Fourier series can be written: ak Cos(kwt)+bk sin(kwt) =ck Cos(kwt+$k) ak Find the ck's and plot their amplitude on a bar graph vs. k to illustrate the relative size of each term in the series. Explain the significance of the plot
Answers
(a) The real discrete Fourier transform (DFT) is calculated for the given data set to analyze the helicopter's acoustic signature.
(b) To obtain the ck values and illustrate the relative size of each term in the Fourier series, we calculate the magnitude of each coefficient and plot their amplitudes on a bar graph against the corresponding frequency component, k.
To analyze the helicopter's acoustic signature, the real DFT is computed for the provided data set. The DFT transforms the time-domain measurements of acoustic pressure into the frequency domain, revealing the different frequencies present and their corresponding amplitudes. This analysis helps in understanding the spectral characteristics of the helicopter's acoustic signature and identifying prominent frequency components.
Using the Fourier series representation, the amplitudes (ck's) of the different frequency components in the Fourier series are determined. These amplitudes represent the relative sizes of each term in the series, indicating the contribution of each frequency component to the overall acoustic signature. By plotting the amplitudes on a bar graph, the relative strengths of different frequency components become visually apparent, enabling a clear comparison of their importance in characterizing the helicopter's acoustic signature.
Learn more about Fourier transform
brainly.com/question/29063535
#SPJ11
Which graph is defined by the function given below?
y = (x-3)(x-3)

Answers
Answer: graph b
Step-by-step explanation:
Vertex: ( 3 ,0 )
Focus: ( 3 , 1 4 )
Axis of Symmetry: x = 3
Directrix: y = − 1 4
In farming, the relationship between precipitation during the growing season and crop yield is quadratic. The following table shows the amount of rainfall (in inches) with corresponding soybean crop yields (in bushels per acre) for an agricultural region.
Rainfall Crop Yield
2.25 42.1
2.75 43.0
3.25 43.8
3.75 44.2
4.25 44.5
4.75 44.3
5.25 43.5
Use a quadratic regression calculator to write a quadratic function that provides a reasonable fit to this set of data.
Answers
Answer:
2.25 42.1
2.75 43.0
3.25 43.8
Step-by-step explanation:
soybean crop yields (in bushels per acre) for an agricultural region.
Rainfall Crop Yield
2.25 42.1
2.75 43.0
3.25 43.8
3.75 44.2
4.25 44.5
4.75 44.3
5.25 43.5
Use a quadratic regression calculator to write a quadratic function that provides a reasonable fit to this set of data
How do you calculate the rate of change of a periodic function
Answers
The rate of change of a periodic function is itself a periodic function. In the case of a sinusoidal wave, the derivative is also a sinusoidal wave with the same period, but shifted by a phase angle of \(π/2.\)
The rate of change of a periodic function at a specific point is equal to the instantaneous slope of the tangent line to the graph of the function at that point.
To calculate the rate of change of a periodic function, you need to take the derivative of the function with respect to the independent variable (usually time). If the function is a sinusoidal wave, you can use trigonometric identities to find the derivative.
For example, let's say we have a function f(t) = sin(t), which represents a sinusoidal wave. To find the rate of change of the function at a particular point t = a, we need to take the derivative of the function with respect to t:
f'(t) = cos(t)
Then we can evaluate this derivative at t = a to find the rate of change at that point:
f'(a) = cos(a)
This tells us the instantaneous rate of change of the function at the point t = a.
Note that the rate of change of a periodic function is itself a periodic function. In the case of a sinusoidal wave, the derivative is also a sinusoidal wave with the same period, but shifted by a phase angle of \(π/2.\)
For such more questions on Periodic Function Derivatives.
https://brainly.com/question/1851537
#SPJ11
4. What are the Z-scores for the following Confidence Interval levels? Remember, you MUST account for both tails of the curve, positive and negative, when identifying each. That means you will need to do a little math to obtain the correct z-value. 3 Points 68%= 85% = 99% =
Answers
In order to calculate the z-scores for the given Confidence Interval (CI) levels, we need to use the Z-table. It is also known as the standard normal distribution table. Here are the z-scores for the given Confidence Interval levels:1. 68% CI: The confidence interval corresponds to 1 standard deviation on each side of the mean.
Thus, the z-score for the 68% \(CI is ±1.00.2. 85% CI\): The confidence interval corresponds to 1.44 standard deviations on each side of the mean.
We can calculate the z-score using the following formula:\(z = invNorm((1 + 0.85)/2)z = invNorm(0.925)z ≈ ±1.44\)Note that invNorm is the inverse normal cumulative distribution function (CDF) which tells us the z-score given a certain area under the curve.3. 99% CI: The confidence interval corresponds to 2.58 standard deviations on each side of the mean. We can calculate the z-score using the following formula:\(z = invNorm((1 + 0.99)/2)z = invNorm(0.995)z ≈ ±2.58\)
Note that in general, to calculate the z-score for a CI level of (100 - α)% where α is the level of significance, we can use the following formula:\(z = invNorm((1 + α/100)/2)\) Hope this helps!
To know more about distribution visit:
https://brainly.com/question/29664127
#SPJ11
two point charges are placed on the x-axis as follows: charge q1 = 3.99 nc is located at x= 0.205 m , and charge q2 = 5.01 nc is at x= -0.302 m .
Answers
Two point charges, q1 = 3.99 nC located at x = 0.205 m and q2 = 5.01 nC at x = -0.302 m, are placed on the x-axis. The electric field and direction at a given point can be calculated using the principle of superposition.
The electric field at a point due to a point charge is given by Coulomb's law, E = kq/r^2, where E is the electric field, k is Coulomb's constant (8.99 x 10^9 Nm^2/C^2), q is the charge, and r is the distance between the point charge and the point where the electric field is being measured. To calculate the net electric field at a point due to multiple charges, we use the principle of superposition, which states that the total electric field at a point is the vector sum of the electric fields due to each individual charge.
In this case, we have two charges, q1 = 3.99 nC and q2 = 5.01 nC. The electric field at a point P on the x-axis, due to q1, can be calculated as E1 = kq1/r1^2, where r1 is the distance between q1 and point P. Similarly, the electric field at point P due to q2 can be calculated as E2 = kq2/r2^2, where r2 is the distance between q2 and point P. To find the net electric field at point P, we add the electric fields vectorially, E_net = E1 + E2.
To learn more about superposition click here: brainly.com/question/12493909
#SPJ11
x - 2/5 = 1/6
what is the answer for x?
Answers
Answer:
17/30
Step-by-step explanation:
Answer:
x=17/30
Step-by-step explanation:
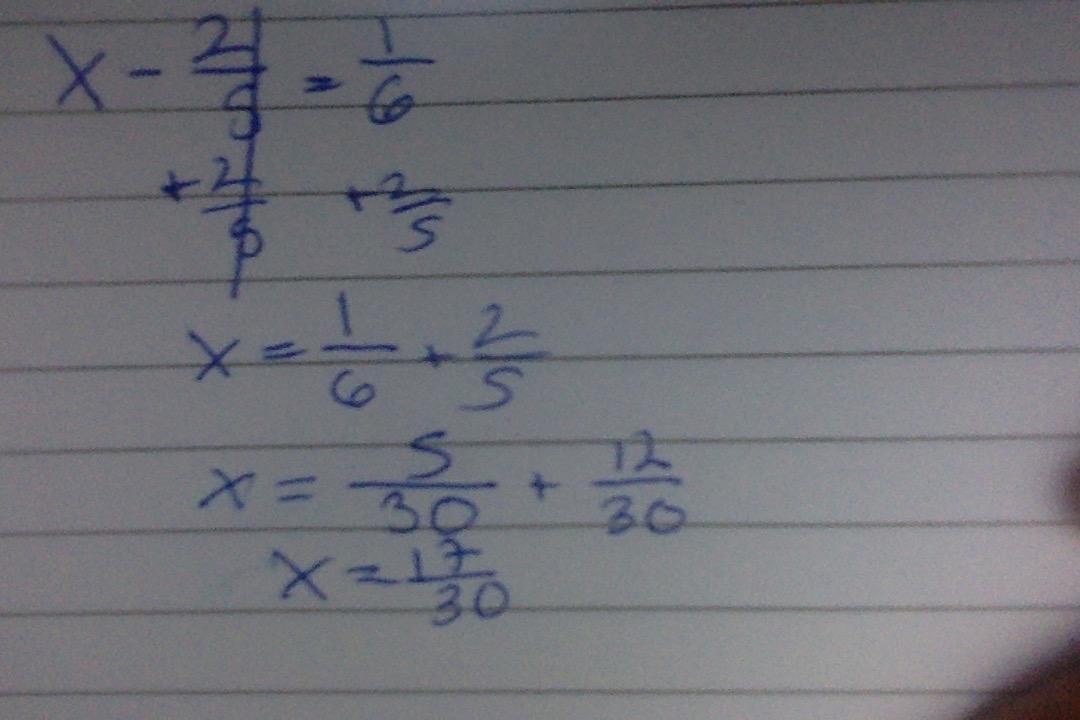
how do you find the zeros of polynomial r^2-28=-3x? Please show steps as I do not understand how to solve this problem. Thank you ^-^
Answers
Answer:
x = -7 and x = 4
Step-by-step explanation:
Note, I am taking the polynomial equation as
\(x^2 - 28 = -3x\)
Otherwise it does not become a polynomial of one variable and cannot be solved
Zeros of a polynomial are the values of x where the polynomial value itself is 0
Standard equation for a polynomial of degree 2 is ax² + bx + c = 0 where a, b and c are constants
Degree is the highest exponent. Here the highest exponent is 2 so the polynomial has degree 2. Such a polynomial is called a quadratic polynomial
So we first have to convert
x² - 28 = - 3x into this form ax² + bx + c
1. Add 3x to both sides
x² - 28 + 3x = -3x + 3x =0
==> x² + 3x - 28 = 0
With a = 1, b = 3 and c = -28
2. Factor x² + 3x - 28 = 0
Here a = 1, b = 3 and c = -28
Factoring means find two expressions x+a and x +b such that (x + a) (x + b) = x² + 3x - 28 = 0
Then we can state that
x + a = 0 ==> x = -a as one solution
x + b = 0 ==> x = -b as the other solution
To factor, find two numbers m and n(could be negative) such that mn = c and m + n = b
28 has factors 7 and 4 so that is a good start
-28 = -7 x 4 or could also be 7 x -4
How do we choose?
Add both and see what gives you +3
-7 + 4 = -3 Nope
7 + -4 = 7-4 = 3 YES
So the factors are 7 and -4
(x + m) = (x + 7)
(x + n) = (x -4)
So the original quadratic polynomial becomes
(x + 7)(x -4) =
This means
x + 7 = 0 ==> x = -7
x - 4 = 0 ==> x = 4
So the solutions(also called roots) of x² + 3x - 28 = 0 are:
x = -7 and x = 4
Both the above values satisfy the quadratic equation
Find the amount accumulated after
investing a principal P for t years at an
interest rate compounded annually.
P = $15,500
r = 9.5%
t = 12
Hint: A = P (1 + ) kt
A = $[?]
Round your answer to the nearest cent (hundredth).

Answers
The amount accumulated after investing a principal P for t years at an interest rate compounded annually is $46,057.58.
How to solve compound interest ?Compound interest is the interest you earn on interest. Compound interest is the interest calculated on the principal and the interest accumulated over the previous period.
Therefore, let's find the amount accumulated after investing a principal P for t years at an interest rate compounded annually.
\(A = p(1 + \frac{r}{n} )^{nt}\)
where
P = principalr = ratet = timen = number of timep = 15,500
r = 9.5%
t = 12
n = 1
\(A = 15500(1 + \frac{0.095}{1} )^{1(12)}\)
A = 15,500.00(1 + 0.095)¹²
A = $46,057.58
learn more on compound interest here: https://brainly.com/question/13803287
#SPJ1
$46,057.58, answer for acellus
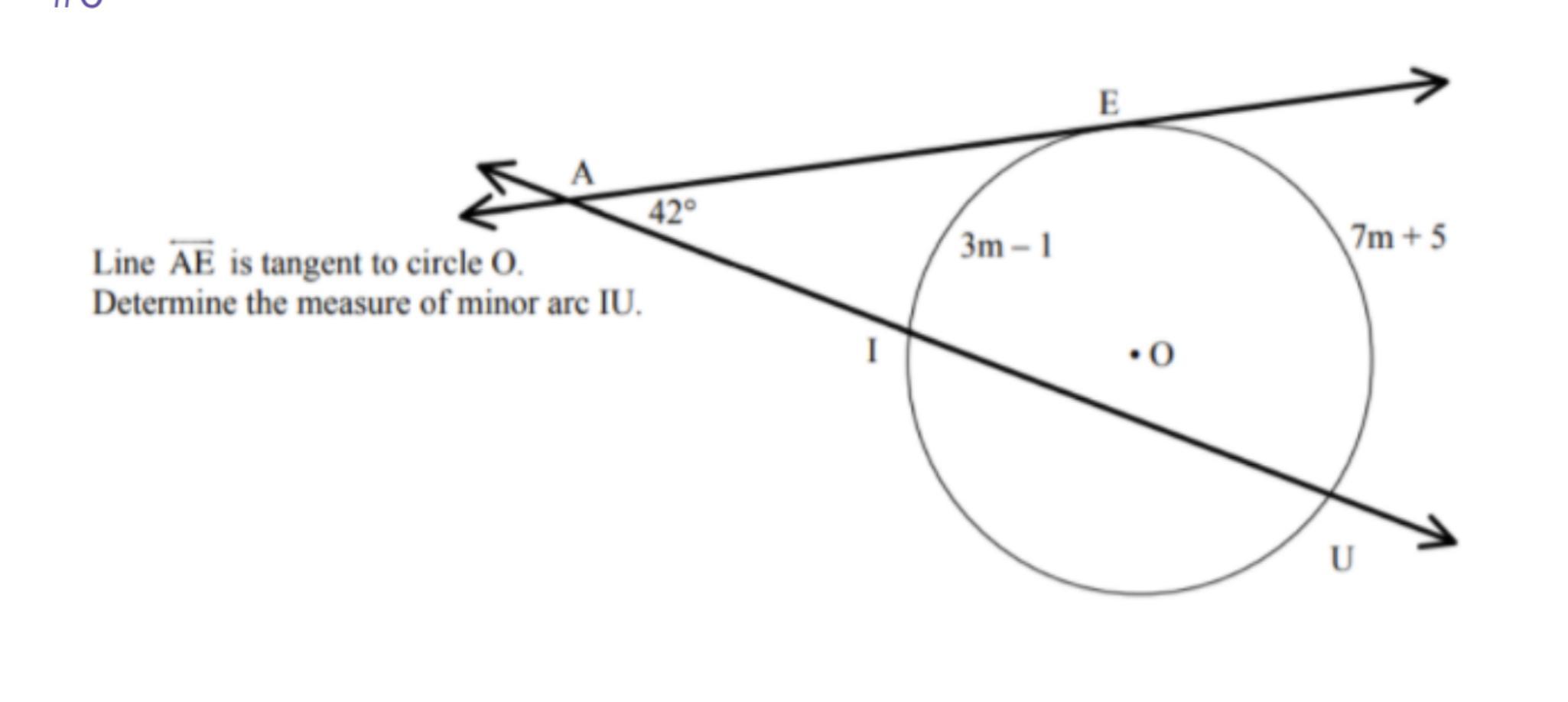
Circle experts...help! will give brainly to most detailed answer
Answers
Answer:
IU=161
Step-by-step explanation:
Angle Formed by Two Secants= 1/2 (difference of Intercepted Arcs)
42 = 1/2 (7m+5 - (3m-1))
Distribute the minus sign
42 = 1/2 (7m+5 - 3m+1))
Combine like terms
42 = 1/2 ( 4m+6)
Distribute the 1/2
42 = 2m+3
Subtract 3 from each side
42-3 = 2m+3-3
39 = 2m
Divide by 2
19.5 = m
The sum of the arcs = 360
IU+ 3m-1 + 7m+5 = 360
IU +10m+4 = 360
IU +10(19.5) +4 = 360
IU +195+4 = 360
IU = 360 - 199
IU=161
Problem - Firms in a competitive market have the following production costs for various levels of output. The market price is currently $4. Quantity Total Cost 0 1 10 2 13 3 18 4 25 34 1. How many units will each firm supply to maximize profit, and how much profit will each firm earn? Show calculations. 2. When the market price is at $4, is the market in long-run equilibrium? Explain your answer. 3. At what price will the market be in long-run equilibrium? Show calculations.
Answers
For various levels of output, businesses in a competitive market have the following production costs. Right now, the price on the market is $4. Total Cost Quantity 0 1 10 2 13 3 18 4 25 34. Therefore,
1. Each firm maximizes profit by supplying 2 units where MR = MC.
2. At $4 market price, market not in long-run equilibrium as ATC ($6.5) > price.
3. Market reaches long-run equilibrium at $6, the minimum point of ATC curve.
To determine the units each firm will supply to maximize profit and calculate the profit, we need to examine the cost and revenue associated with each quantity of output.
Quantity Total Cost
0 1
1 10
2 13
3 18
4 25
1. To find the quantity that maximizes profit for each firm, we need to compare the marginal cost (MC) and marginal revenue (MR) at each quantity level.
Quantity Total Cost MC MR
0 1 - -
1 10 9 4
2 13 3 4
3 18 5 4
4 25 7 4
To maximize profit, a firm will produce where MR equals MC. Looking at the table, we can see that at a quantity of 2, the MR and MC are equal. Therefore, each firm will supply 2 units to maximize profit.
2. To determine if the market is in long-run equilibrium at a market price of $4, we need to compare the market price with the average total cost (ATC) for each firm. If the market price is equal to or greater than the ATC, the market is in long-run equilibrium.
Let's calculate the ATC for each firm at a quantity of 2:
\(ATC = \frac{Total Cost}{Quantity}\)
\(ATC = \frac{13}{2}\)
ATC = 6.5
The ATC for each firm is $6.5, which is greater than the market price of $4. Therefore, the market is not in long-run equilibrium because firms are not covering their costs and would not continue to operate in the long run.
3. To determine the price at which the market will be in long-run equilibrium, we need to find the minimum point of the average total cost (ATC) curve. This point represents the price at which firms can cover their costs and earn a normal profit in the long run.
Looking at the table, we can observe that the minimum ATC occurs at a quantity of 3. Let's calculate the ATC at this quantity:
\(ATC = \frac{Total Cost}{Quantity}\)
\(ATC = \frac{18}{3} = 6\)
Therefore, the market will be in long-run equilibrium at a price of $6, which corresponds to the minimum point of the ATC curve.
To know more about the average total cost curve refer here,
https://brainly.com/question/14869550#
#SPJ11
I NEED THIS NOW PLEASE
Casey wants to buy a gym membership. One gym has a $120 joining fee and costs $40 per month. Another gym has no joining fee and costs $70 per month. When would Casey pay the same amount to be a member of either gym? How much would he pay?
Answers
Subtract 40 from 70 and you get 30
Then you divide 30 into 120 and you get 4.
So in 4 months he will pay the same.
Once you get that.
You plug 4 into. 120+40(4)=280
As well as the other gym option. Which is the 70 per month. So 70(4)=280.
So in the end he will end up paying the same amount for both gyms. So either one he chooses will be a win win. Even with the 120 joining fee. I do hope this help.
Consider the graph of the function f{x} = -{2}^x + 4
What is the range of function f?


Answers
The range of the function f(x) = \(-2^{x}\) + 4 is -∞ < y < 4.
What is range of a function?
All potential values for y are included in a function's range. The equation to determine a function's range is Y = f. (x). If every x value has exactly one y value, then it is merely a function in a relation.
We are given a function which is defined as f(x) = \(-2^{x}\) + 4.
We know that range is the output we get after substituting the value of x.
So, in this situation, we will get the value for y less than 4 or equal to 4 because when x = 0, we will get 4 and when x = 1, we will get 2 as there is a minus sign before 2 due to which this will be always a negative value.
Thus, the range of the function will be -∞ < y < 4.
Hence, the third option is the correct option.
Learn more about range from the given link
https://brainly.com/question/7954282
#SPJ1
Joe walked is dog 3/3 mile every morning how much mike did he walked his dog every morning
Answers
Answer:
1 mile.
Step-by-step explanation:
3/3 mile is equal to 1 mile.
Answer:
Joe walked his dog 1 mile.
Step-by-step explanation:
3/3 =1 mile.
Click and drag like terms onto each other to simplify fully.
2-5+7y-5x+7x-2y
Answers
Answer: 5y + 2x - 3
(In simplest form)
given two sides of a triangle, find a range of possible lengths for the third side. a) 24 ft, 52 ft answer < x < answer b) 16 km, 17 km answer < x < answer
Answers
The range of possible lengths for the third side be
0 ft < x < 76 ft
0 ft < x < 33 ft
Given, two sides of a triangle
we have to find the range of possible length for the third side of the triangle.
a) 24 ft and 52 ft
given first side of the triangle be, 24 ft
and second side of the triangle be, 52 ft
as we know that the third side should be less than the sum of the remaining two sides of any triangle.
So, let the third side be x
x < 24 + 52
x < 76
Therefore, the third side should be less than 76 ft and obviously greater than 0 ft.
Range of the third side be, 0 ft < x < 76 ft
b) 16 ft and 17 ft
given first side of the triangle be, 16 ft
and second side of the triangle be, 17 ft
as we know that the third side should be less than the sum of the remaining two sides of any triangle.
So, let the third side be x
x < 16 + 17
x < 33
Therefore, the third side should be less than 33 ft and obviously greater than 0 ft.
Range of the third side be, 0 ft < x < 33 ft
Hence, the range of possible lengths for the third side be
0 ft < x < 76 ft
0 ft < x < 33 ft
Learn more about Sides of Triangles here https://brainly.com/question/22407545
#SPJ4
need help with number 8

Answers
Answer:
x = 14 2/3
Step-by-step explanation:
it is a parallelogram.
that means AB is parallel to CD, and AD to BC.
it also means that the total angles at B and D must be equal. and the total angles at A and C.
and the sum of all angles in a parallelogram is 360 degrees.
so, we have
360 = 2×(4x + 4x + 8) + 2×(x + 10 + 2x + 8) =
= 8x + 7x + 16 + 2x + 20 + 4x + 16 =
= 21x + 52
308 = 21x
x = 14.666666666.... = 14 2/3
What is the measurement of angle C? Part C
Answers
Forgot picture
Answer:
130 degrees is your answer
Step-by-step explanation:
The measurement of angle C is given by the expression 180° – 25° – 25°. So, angle C measures 130°.- answer from edmentum
4/5 divided by 1/10 = ? to solve this problem aske the question......\ the quotient is
Answers
Given:
\(\begin{gathered} \frac{(\frac{4}{5})}{\frac{1}{10}}=\frac{4}{5}\times\frac{10}{1} \\ =\frac{4\times10}{5\times1} \\ =\frac{40}{5} \\ =8 \end{gathered}\)Thus, the answer of 4/5 divided by 1/10 is 8.
Suppose there are five processes, their arrival time and running time are listed as follows. Adopt FCFS and SJF, respectively, give the schedule order and average waiting time. (12) 1) Give the schedule order of FCFS. (3) 2) Compute the average waiting time of FCFS. (3) Give the schedule order of SJF. (3) 3) 4) Compute the average waiting time of SJF. (3) Process Arrival time Running time Pl 0 3 P2 3 10 P3 4 6 P4 5 1
Answers
Average waiting time for FCFS: 8.75
SJF schedule order: Pl -> P4 -> P3 -> P2Average waiting time for SJF: 4.75
To solve this scheduling problem using FCFS (First-Come, First-Served) and SJF (Shortest Job First) algorithms, let's go step by step:
Schedule order for FCFS:
The FCFS algorithm schedules processes based on their arrival time. So, the schedule order for FCFS is as follows:
Pl -> P2 -> P3 -> P4
Average waiting time for FCFS:
To compute the average waiting time for FCFS, we need to calculate the waiting time for each process and then take the average.
Process | Arrival Time | Running Time | Waiting Time
Pl | 0 | 3 | 0
P2 | 3 | 10 | 3
P3 | 4 | 6 | 13
P4 | 5 | 1 | 19
Average waiting time = (0 + 3 + 13 + 19) / 4 = 8.75
Therefore, the average waiting time for FCFS is 8.75.
Schedule order for SJF:
The SJF algorithm schedules processes based on their running time. The process with the shortest running time gets executed first. If multiple processes have the same running time, the process with the earliest arrival time is selected first. The schedule order for SJF is as follows:
Pl -> P4 -> P3 -> P2
Average waiting time for SJF:
To compute the average waiting time for SJF, we need to calculate the waiting time for each process and then take the average.
Process | Arrival Time | Running Time | Waiting Time
Pl | 0 | 3 | 0
P4 | 5 | 1 | 3
P3 | 4 | 6 | 6
P2 | 3 | 10 | 10
Average waiting time = (0 + 3 + 6 + 10) / 4 = 4.75
Therefore, the average waiting time for SJF is 4.75.
To know more about FCFS :
brainly.com/question/32861141
#SPJ11
Please help me I don’t understand it at all

Answers
Answer:
The second choice; KJL and HGJ
Step-by-step explanation:
These 2 angles are corresponding angles
find a function f such that f '(x) = 3x^2 + 6x + 5. are there any other functions that satisfy this?
Answers
The one function that satisfies f '(x) = 3x² + 6x + 5 is f(x) = x³ + 3x²÷2 + 5x + C. where C is the constant of integration.
How we find the function?The given function's derivative is f'(x) = 3x² + 6x + 5.
To find the original function f(x), we need to integrate the derivative.
We can integrate the given function f'(x) term by term, using the power rule of integration:
∫f'(x) dx = ∫(3x² + 6x + 5) dx
f(x) = x^3 + 3x²÷2 + 5x + C
Any constant value of C can be added to the above function, resulting in an infinite number of functions that satisfy
f '(x) = 3x² + 6x + 5.
f(x) = x^3 + 3x²÷2 + 5x + 2 and f(x) = x³ + 3x²÷2 + 5x - 7 are both valid solutions to f '(x) = 3x² + 6x + 5, with different constant values of C.
This is because the constant of integration represents an arbitrary constant, and when we take the derivative, the constant term becomes zero. Hence, any function that differs from the original function by a constant value will also have the same derivative.
Learn more about Function
brainly.com/question/12426369
#SPJ11
y =-4x – 5y = 3x- 2Is (3,7) a solution of the system?Choose 1 answer:YesNo

Answers
To be a solution of the system, it has to be true in both equations.
As the coordinate is (x,y), then we have to replace 3 in every x in the equations and 7 in every y in the equations.
• Equation 1
\(y=-4x-5\)\(7=-4\cdot3-5\)\(7=-12-5\)\(7=-17\)As this is NOT TRUE, then it is not a solution for this equation, and as we are looking for a solution for the system of equations, then this is not a solution.
Answer: B. No
Use the spinner to find the odds in favor of stopping on a number greater than 10.

Answers
Answer:
7:10
Step-by-step explanation:
1. There are a total of 10 sections, each with a different number.
2. Out of all these sections, 3 sections are less than 10 and 7 are greater than 10.
This means that 7 out of 10 numbers are greater than 10.To write this statement as a ratio, we can rewrite the two numbers in the ratio of numerator to denominator: 7:10Therefore, the odds are 7:10.
A watchman was paid basic wage of $250.00 a day. If he worked everyday in the month, calculate his basic wage for February, 1988.
A. $6,250.00
B. $7,200.00
C. $7,250.00
D. $7,500.00
Answers
Answer:
Since February 1988 is a leap year, February has 29 days in it. Multiply 29 times $250.00 to get C. $7,250.00.
The area of a square is 100 m². What is its perimeter?
Answers
Answer:
hope it helps you.........

Answer:
correct me if I'm wrong but 40?