REPOST*
Which equation or inequality shows the relationship between the plotted points on the number line
A. 3 < -6
B.-6 > -3.
C.-6 < -3
D.-3 < -6
Answers
Answer:
C
Step-by-step explanation:
-6 is more to the left of the number line than -3
Related Questions
Use an adaptive weighting scheme to reduce the effects of outliers on linear least squares fitting. Read x y points (from a file named on the command line or from standard input) and fit a line (i.e., c0 + c1x = y) to the points using weighted least squares. Output the coefficients c of the initial fit and of the final fit. Use the following iterative weighting approach: 1: Initialize all weight values wi = 1.0, 0 ≤ i < n for n points and place as the diagonal values of an n × n matrix W. All off diagonal values of W are zero. 2: Initialize line coefficients cold to large real values . (i.e., sys.float info.max in Python or std::numeric limits::max() in C++). 3: for loop from 0 to MaxIterations do 4: Solve the weighted least squares problem for coefficients c using the normal equations approach:
Answers
To reduce the effects of outliers on linear least squares fitting, we can use an adaptive weighting scheme. The approach involves initializing all weight values to 1.0 and placing them as diagonal values of an n × n matrix W. All off-diagonal values of W are set to zero. We then initialize the line coefficients to large real values.
Next, we use an iterative approach to update the weights and re-estimate the line coefficients. In each iteration, we calculate the residuals (i.e., the difference between the observed and predicted values) and use them to update the weights. Specifically, we set wi = 1/(residuali^2), where residual is the residual for the ith data point. We then update the weight matrix W with the new weight values.
We then solve the weighted least squares problem for coefficients c using the normal equations approach. This involves multiplying the transpose of the design matrix X with the weight matrix W and the response vector y and then solving for c using the resulting equation: (X^T)WXc = (X^T)Wy.
We repeat the above steps until convergence or until we reach a predetermined maximum number of iterations. Finally, we output the coefficients c of the initial fit and of the final fit. The initial fit is obtained using the original weight matrix with all values set to 1.0, while the final fit is obtained using the converged weight matrix with updated weight values.
Learn more about adaptive weighting scheme here:
https://brainly.com/question/12993120
#SPJ11
The table shows values for a quadratic function.
What is the average rate of change for this function for the interval from x = 1
to x = 3?

Answers
The average rate of change for this function for the interval from x = 1
to x = 3 will be 8. Therefore option B is correct.
How to find the average rate of change of something?Let the thing that is changing be y and the thing with which the rate is being compared is x, then we have the average rate of change of y as x changes as:
\(\text{Average rate} = \dfrac{y_2 - y_1}{x_2 - x_1}\)
where when
\(x = x_1, y = y_1\\and \\x = x_2, y = y_2\)
The average rate of change can be calculated as;
From x=1 to x=3,
y = 2 and y = 18
Therefore, based on the table, when:
\(x_1 = 1 y_1 = 2 \\and \\x_2 = 3, y_2 = 18\)
Then:
\(\text{Average rate} = \dfrac{y_2 - y_1}{x_2 - x_1}\)
\(\text{Average rate} = \dfrac{18 - 2}{3-1}\\\\\text{Average rate} = \dfrac{16}{2}\\\\\text{Average rate} = 8\)
Therefore option B is correct.
Learn more about average;
https://brainly.com/question/12424098
#SPJ1
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
A sample of bacteria taken from a river has an initial concentration of 2.1 million bacteria per milliliter and its concentration triples each week. (a) Find an exponential model that calculates the concentration after x weeks. (b) Estimate the concentration after 1.6 weeks. (a) B(x) = (Type an equation usingx as the variable.)
Answers
The exponential model that calculates the concentration of bacteria after x weeks can be represented by the equation B(x) = 2.1 million * (3^x), the concentration after 1.6 weeks would be approximately 14.87 million bacteria per milliliter.
This equation assumes that the concentration triples each week, starting from the initial concentration of 2.1 million bacteria per milliliter.
To estimate the concentration after 1.6 weeks, we can substitute x = 1.6 into the exponential model. B(1.6) = 2.1 million * (3^1.6) ≈ 14.87 million bacteria per milliliter. Therefore, after 1.6 weeks, the estimated concentration of bacteria in the river would be approximately 14.87 million bacteria per milliliter.
The exponential model B(x) = 2.1 million * (3^x) represents the concentration of bacteria after x weeks, where the concentration triples each week. By substituting x = 1.6 into the equation, we estimate that the concentration after 1.6 weeks would be approximately 14.87 million bacteria per milliliter.
Learn more about equation here:
https://brainly.com/question/29538993
#SPJ11
Combine like terms to create an equivalent expression 2/5m- 4/5 -3/5
Answers
Answer:
2/5m - 7/5
Step-by-step explanation:
Combine the like terms (-4/5 and -3/5)
Last question need to be answered in less than 5 mins

Answers
Answer:
Step-by-step explanation:
492
HELP ASAP LAST QUESTION I PROMISE

Answers
Answer:
\(a=36\: \sf ms^{-2}\)
Step-by-step explanation:
\(\textsf{Displacement}\:x=4t^3-27t+8\)
\(\implies \textsf{Velocity}\:v=\dfrac{dx}{dt}=12t^2-27\)
\(\implies \textsf{Acceleration}\:a=\dfrac{dv}{dt}=24t\)
At the moment the direction of motion of P reverses, the velocity of P will be zero. Therefore, find the value of t when v = 0:
\(\implies v=0\)
\(\implies 12t^2-27=0\)
\(\implies t^2=\dfrac{27}{12}=\dfrac94\)
\(\implies t=\pm\sqrt{\dfrac94}=\pm\dfrac32\)
As time is positive, P reverses when t = 3/2 s
To find acceleration at this time, simply substitute the found value of t into the equation for acceleration:
\(\implies a=24(\frac32)\)
\(\implies a=36\: \sf ms^{-2}\)
see look it says it is wrong

Answers
Answer:
21 ft.Step-by-step explanation:
Not area. Perimeter.
Simple way:
4.25 + 6.25 + 4.25 + 6.25Advanced way:
(4.25 + 6.25)*2Solve:
4.25 + 4.25 + 3.25 + 6.25= 8.5 + 12.5= 21.Solve:
(4.25 + 6.25)*2= 10.5 * 2= 21.Your answer is 21.
Give an example of a fraction that is sometimes used to approximate pi?
Answers
A fraction that is sometimes used to approximate pi is 22/7.
What is fraction that is sometimes used to approximate pi?One example of a fraction that is sometimes used to approximate pi is 22/7. This fraction is an approximation of pi that has been used for centuries, even though it is not an exact value of pi.
It is a good approximation that is accurate to within about 0.04%, which makes it useful in many practical applications.
The fraction 22/7 comes from dividing the circumference of a circle by its diameter, which is the definition of pi. While the exact value of pi is an irrational number that cannot be expressed as a fraction, 22/7 is a commonly used approximation that is easy to remember and calculate with. However,
there are more accurate approximations of pi that can be used for more precise calculations, such as 355/113 or 3.14159265359.
To know more about Greek symbols visit:
brainly.com/question/7269995
#SPJ1
-2w + 15= -3/2 Find w
Answers
Answer:
w = 33/4 or 8 1/4
Step-by-step explanation:
-2w + 15= -3/2
Solve for w
Multiply each side by 2
-4w + 30 = -3
Subtract 30 from each side
-4w + 30 -30 = -3-30
-4w = -33
Divide by -4
-4w/-4 = -33/-4
w = 33/4
w = 8 1/4
Answer:
Step-by-step explanation:

find the value of y when x equals -1.
8x - 2y =10
Answers
Answer:
y = - 9
Step-by-step explanation:
Substitute in -1 for x
8(-1) - 2y = 10
-8 - 2y = 10
Subtract -8 from both sides
-8 - (-8) cancels out to 0
10 - (-8) = 18
We are left with:
-2y = 18
Divide by -2 on both sides.
-2y/-2 = y
18/-2 = -9
y = -9
Show how to find m<1 using the inverse cos of <1.

Answers
\(\text{We know that,}\\\\\cos \theta = \dfrac{\text{Base}}{\text{Hypotenuse}}\\\\\\\text{For}~ \angle1,\\\\~~~~~~\cos \angle 1 = \dfrac bc\\\\\\\implies \cos \angle 1 = \dfrac 35\\\\\\\implies \angle 1 = \cos^{-1} \left( \dfrac 35 \right)\\\\\\\implies \angle 1 = 53.13^{\circ}\\\\\\\text{For} ~ \angle 2,\\\\~~~~~~~\cos \angle 2 = \dfrac ac\\\\\\\)
\(\implies \cos \angle 2 = \dfrac 45\\\\\\\implies \angle 2 =\cos^{-1} \left( \dfrac 45 \right)\\ \\\\\implies \angle 2 = 36.86^{\circ}\)
\(\text{Hence,}~~ m\angle 1 = 53.13^{\circ}~~ \text{and}~~ m\angle 2 =36.86^{\circ}.\)
The base of a regular pyramid is a hexagon.
Answers
Answer:
The base of the regular pyramid is a square.
Step-by-step explanation:
The number of computer shutdowns during any month has a Poisson Distribution, averaging 0.25 shutdowns per month.
A) What is the porbability of at least 3 computers shutdowns during the year?
B) During the next year, what is the probability of at least 3 months (Out of 12) with exactly 1 computer shutdown in each?
Answers
The probability of at least 3 computer shutdowns during the year is 0.6472 or 64.72%. The probability of at least 3 months with exactly 1 shutdown is 0.5886 or 58.86%.
The number of shutdowns during the year has a Poisson Distribution with parameter λ = 0.25 * 12 = 3. We want to find the probability of at least 3 shutdowns during the year, which is:
P(X >= 3) = 1 - P(X < 3)
Using the cumulative distribution function (CDF) for the Poisson Distribution, we get:
P(X < 3) = F(2) = e^(-λ) * (λ^0/0! + λ^1/1!) + e^(-λ) * (λ^2/2!) = e^(-3) * (1 + 3 + 9/2) = 0.3528
Therefore, P(X >= 3) = 1 - P(X < 3) = 1 - 0.3528 = 0.6472
The number of months with exactly 1 shutdown during the year has a Poisson Distribution with parameter λ = 0.25. The probability of a month having exactly 1 shutdown is:
P(X = 1) = e^(-λ) * (λ^1/1!) = 0.25 * e^(-0.25)
The number of months with exactly 1 shutdown in a year has a Binomial Distribution with parameters n = 12 and p = P(X = 1). We want to find the probability of at least 3 months with exactly 1 shutdown, which is:
P(X >= 3) = 1 - P(X < 3)
Using the cumulative distribution function (CDF) for the Binomial Distribution, we get:
P(X < 3) = F(2) = Σ (12 choose k) * p^k * (1-p)^(12-k), for k = 0 to 2
P(X < 3) = (12 choose 0) * 0.25^0 * 0.75^12 + (12 choose 1) * 0.25^1 * 0.75^11 + (12 choose 2) * 0.25^2 * 0.75^10
P(X < 3) = 0.4114
Therefore, P(X >= 3) = 1 - P(X < 3) = 1 - 0.4114 = 0.5886
To know ore about Probability:
https://brainly.com/question/11234923
#SPJ4
Write the equation for the line that contains the points (5,6) and (10,12). [No picture this is the full question]
Answers
Answer:
y=1 and 1/5x
Step-by-step explanation:
Explain how you know that x^2-8x+20 is always positive.
Please help.
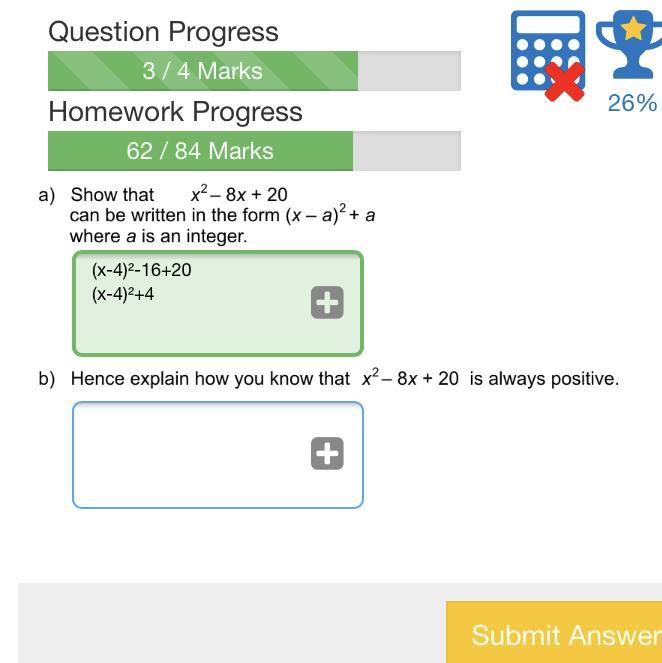
Answers
Answer:
if you rearrange to complete the square, you get (x^2-4)^2 +4
and seeing as anything squared will always be positive or zero, the lowest possible value for (x^2-4)^2 is 0, when x = 4
and 0 + 4 = 4, which is greater than 0, so positive
Step-by-step explanation:
We have x^2-8x+20 is always positive.
What is equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign. In its simplest form in algebra, the definition of an equation is a mathematical statement that shows that two mathematical expressions are equal. For instance, 3x + 5 = 14 is an equation, in which 3x + 5 and 14 are two expressions separated by an 'equal' sign.
here, we have,
x^2-8x+20
=x^2-2.x.4+16+4
if you rearrange to complete the square,
you get (x^2-4)^2 +4
and seeing as anything squared will always be positive or zero,
the lowest possible value for (x^2-4)^2 is 0, when x = 4
and 0 + 4 = 4, which is greater than 0,
so, positive.
To learn more on equation click:
brainly.com/question/24169758
#SPJ2
solve the quadratic equation \(3x^{2} +x-5=0\)
give your answers to 2 decimal places
Answers
Answer:
-1.47, 1.14 to 2 decimal places.
Step-by-step explanation:
3x^2 + x - 5 = 0
3(x^2 + 1/3x) - 5 = 0
Completing the square on the expression in the parentheses:
3[(x + 1/6)^2 - 1/36) - 5 = 0
3(x + 1/6)^2 - 1/12 - 5 = 0
(x + 1/6)^2 = 61/12 / 3
(x + 1/6)^2 = 61/36
(x + 1/6) = +/-√61 / 6
x = -1/6 +/- √61 / 6
x = 1.135, -1.468
If real gdp in a particular year is $80 billion and nominal gdp is $240 billion, the gdp price index for that year is 100. 300. 240. 200.
Answers
Answer:
If real GDP in a particular year is $80 billion and nominal GDP is $240 billion, the GDP price index for that year is: 300.
Step-by-step explanation:
What happens to the value of the expression 100-x as x increases
Answers
The number 100-x has a decreasing worth as x rises.
What does a mathematical expression look like?A mathematical statement is referred to as an expression or an algebraic expression if it contains numbers, factors, and a numerical operation between them..For example, the arithmetic sign + separates the terms 4m and 5 from of the variable m in the expression 4m + 5..
The number 100-x has a decreasing worth as x rises. This is due to the fact that the phrase 100-x denotes a linear equation with a -1 slope. This indicates that the expression's value drops by one for each unit rise in x. As a result, the expression's value decreases as x increases. For instance, if x is 50, the expression's value is 50; however, if x is 70, the expression's value is 30. The meaning of the equation decreases in proportion to how much x increases.
To know more about Expression visit:
https://brainly.com/question/1859113
#SPJ1
19. What is the distance between P(-3, 10 ) and Q( 12, -6 )? Round to the nearest hundredth
if necessary. d=
Answers
Answer:
To calculate the distance between two points, we can use a formula that is a variation Pythagorean Theorem. Look:
"d" represents the distance and coordinates are expressed as follows: (x, y)
Let's go to the calculations.
The answer is 12,6 u.c.
Step-by-step explanation:
In the given figure ABCD, prove that
angleBCD= angleBAD+ angle ABC+angle ADC.
[Hint: Join A and C then extended AC to the point E]

Answers
We have proved that Angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
To prove that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, we can use the following steps:
Step 1: Join points A and C with a line segment. Let's label the point where AC intersects with line segment BD as point E.
Step 2: Since line segment AC is drawn, we can consider triangle ABC and triangle ADC separately.
Step 3: In triangle ABC, we have angle B + angle ABC + angle BCA = 180 degrees (due to the sum of angles in a triangle).
Step 4: In triangle ADC, we have angle D + angle ADC + angle CDA = 180 degrees.
Step 5: From steps 3 and 4, we can deduce that angle B + angle ABC + angle BCA + angle D + angle ADC + angle CDA = 360 degrees (by adding the equations from steps 3 and 4).
Step 6: Consider quadrilateral ABED. The sum of angles in a quadrilateral is 360 degrees.
Step 7: In quadrilateral ABED, we have angle BAD + angle ABC + angle BCD + angle CDA = 360 degrees.
Step 8: Comparing steps 5 and 7, we can conclude that angle B + angle BCD + angle D = angle BAD + angle ABC + angle ADC.
Step 9: Rearranging step 8, we get angle BCD = angle BAD + angle ABC + angle ADC.
Therefore, we have proved that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
For more questions on Angle .
https://brainly.com/question/31615777
#SPJ8
Given: Quadrilateral \(\displaystyle\sf ABCD\)
To prove: \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\)
Proof:
1. Draw segment \(\displaystyle\sf AC\) and extend it to point \(\displaystyle\sf E\).
2. Consider triangle \(\displaystyle\sf ACD\) and triangle \(\displaystyle\sf BCE\).
3. In triangle \(\displaystyle\sf ACD\):
- \(\displaystyle\sf \angle ACD = \angle BAD + \angle ADC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).4. In triangle \(\displaystyle\sf BCE\):
- \(\displaystyle\sf \angle BCE = \angle BAD + \angle ABC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).5. Since \(\displaystyle\sf \angle BCE\) and \(\displaystyle\sf \angle BCD\) are corresponding angles formed by transversal \(\displaystyle\sf BE\):
- \(\displaystyle\sf \angle BCE = \angle BCD\).6. Combining the equations from steps 3 and 4:
- \(\displaystyle\sf \angle BCD = \angle ACD = \angle BAD + \angle ADC\). - \(\displaystyle\sf \angle BCD = \angle BCE = \angle BAD + \angle ABC + \angle ADC\).Therefore, we have proven that in quadrilateral \(\displaystyle\sf ABCD\), \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
the teacher workroom has a small room used for the meetings that it shaped like a square . if one wall measures 8 feet what is the area of the floor of that meeting room
Answers
The area of the teacher workroom is 64 feet squared
make x the subject of the formula
x/2c = a + 4
Answers
Answer:
x=8c
or
x=8
Step-by-step explanation:
Hope that helps :)
the given scatterplot shows the average annual global surface temperature, in degrees celsius, for each year from 2000 to 2015. the line drawn is the least squares line for the data set.
Answers
The scatterplot with the least squares line provides insights into the relationship between average annual global surface temperature and the years from 2000 to 2015, allowing us to assess trends, strength of correlation, and make predictions within certain limitations.
The scatterplot represents the relationship between the average annual global surface temperature, in degrees Celsius, and the corresponding years from 2000 to 2015. The line drawn on the plot is the least squares line, which is the best fit line that minimizes the overall distance between the observed data points and the line.
The least squares line is determined using a statistical method called linear regression. It calculates the equation of a straight line that represents the trend in the data. This line serves as a mathematical model to estimate the average temperature based on the year.
By analyzing the scatterplot and the least squares line, we can make several observations. Firstly, we can see whether the temperature has been increasing, decreasing, or remaining relatively stable over the given years. If the slope of the line is positive, it indicates a positive correlation, implying that the temperature has been increasing. Conversely, a negative slope suggests a decreasing trend.
Additionally, we can evaluate the strength of the relationship between temperature and time by examining how closely the data points cluster around the line. If the points are closely grouped around the line, it suggests a strong correlation, indicating that the line is a good representation of the data. On the other hand, if the points are more scattered, the correlation may be weaker.
Furthermore, the line can be used to predict the average annual global surface temperature for future years beyond the data range of 2000 to 2015. However, it's important to note that such predictions should be made with caution and considering other factors that may affect global temperatures, such as climate change and natural variability.
for such more question on least squares
https://brainly.com/question/3617398
#SPJ8
Question
The given scatterplot shows the average annual global surface temperature, in degrees celsius, for each year from 2000 to 2015. the line drawn is the least squares line for the data set.
9 3/4 as a percent step by step
Answers
Answer:
9 3/4 in a percent is 975%.
If you change 9 3/4 into a decimal, it will be 9.75, and 9.75 converted into a percent is 975%
What is the value of the expression 12 x (-1.6)
Answers
Answer: -19.2
Step-by-step explanation:
the total bank loan for a car is $15, 265. the bank withdrawals $295.80 each month to pay off the car. write a formula to represent this sequence
Answers
15625=295.80x is the expression for the given condition.
What is expression?An expression or mathematical expression is a finite collection of symbols that is well-formed according to context-dependent norms. In mathematics, an expression is a phrase that has at least two numbers or variables and at least one arithmetic operation. Addition, subtraction, multiplication, or division are all examples of math operations. A number, a variable, or a combination of numbers, variables, and operation symbols constitutes an expression. An equation consists of two expressions joined by an equal sign. Example of a word: the sum of 8 and 3. Example of a word: The product of 8 and 3 equals 11. 8 + 3 is an expression.
Here,
Let x be the number of month to payout.
15625=295.80x
x=52.82
The expression for given condition is 15625=295.80x.
To know more about expression,
https://brainly.com/question/30091997
#SPJ4
whats your yes and no
Answers
A new type of organic pesticide has been developed and will be marketed if it is at least as effective as its chemical-based competitor. List the null hypothesis, alternate hypothesis, and describe the Type I and Type II errors that could result, in this context.
Answers
Null Hypothesis (H0): The new organic pesticide is equally effective as the chemical-based competitor.
Alternative Hypothesis (H1): The new organic pesticide is more effective than the chemical-based competitor.
Type I error: Rejecting the null hypothesis when it is true, i.e., concluding that the new organic pesticide is more effective when it is not.
Type II error: Failing to reject the null hypothesis when it is false, i.e., concluding that the new organic pesticide is not more effective when it is.
In the context of comparing the effectiveness of a new organic pesticide with a chemical-based competitor, we can define the null hypothesis (H0) and the alternative hypothesis (H1) as follows:
Null Hypothesis (H0): The new organic pesticide is equally effective as the chemical-based competitor.
Alternative Hypothesis (H1): The new organic pesticide is more effective than the chemical-based competitor.
Type I error (False Positive): This error occurs when we reject the null hypothesis (H0) when it is actually true.
In this context, a Type I error would be made if we conclude that the new organic pesticide is more effective than the chemical-based competitor when it is actually not.
It means we would falsely accept the alternative hypothesis (H1) and market the organic pesticide as more effective, even though it is not.
Type II error (False Negative): This error occurs when we fail to reject the null hypothesis (H0) when it is actually false.
In this context, a Type II error would be made if we conclude that the new organic pesticide is not more effective than the chemical-based competitor when it is actually better.
It means we would fail to accept the alternative hypothesis (H1) and miss the opportunity to market the organic pesticide, even though it is effective.
The choice of the Type I and Type II errors depends on the risks associated with the decision.
In this case, a Type I error could lead to marketing an organic pesticide that is not actually effective, potentially causing financial losses and damage to the company's reputation.
On the other hand, a Type II error could result in missing out on marketing a genuinely effective pesticide, leading to lost opportunities and potential revenue.
To make an informed decision, it is important to consider the desired level of significance (alpha) and power (1 - beta) in hypothesis testing. These values determine the acceptable trade-off between Type I and Type II errors and depend on factors such as the importance of the outcome and the costs associated with the errors.
For similar question on null hypothesis.
https://brainly.com/question/25263462
#SPJ11
Who sang Will the Circle Be Unbroken with the Nitty Gritty Dirt Band?
Answers
The most famous version of the song was recorded by the Nitty Gritty Dirt Band. "Will the Circle Be Unbroken" is a traditional Christian hymn that has been recorded by many artists over the years.
However, the most famous version of the song was recorded by the Nitty Gritty Dirt Band in 1972 as a collaborative project that featured a wide variety of country, bluegrass, and folk musicians, including legends such as Mother Maybelle Carter, Earl Scruggs, and Doc Watson. The three-disc album was a critical and commercial success and helped to popularize traditional country and bluegrass music among a wider audience. The Nitty Gritty Dirt Band's rendition of "Will the Circle Be Unbroken" remains a beloved classic in the history of American music.
Find more about Nitty Gritty Dirt Band
brainly.com/question/6061970
#SPJ4