Rene is three times as old as his sister Rosy. In 5 years, he will be twice as old as his sister Rosy. What is Rene’s present age?
Answers
Therefore, Rene's age is 15

Related Questions
1. Why might the Federal Reserve change the discount rate?
A. to prompt financial institutions to alter their lending activity
B. to signal financial institutions to purchase government securities
C. to encourage financial institutions to hold excess reserves for profit
D. to convince financial institutions to decrease their cash on deposit
2. A marginal tax on consumers shifts the demand curve to the left, all other things being even. A marginal tax on sellers of a good shifts the….
A. supply curve to the right.
B. supply curve to the left.
C. demand curve to the right.
D. demand curve to the left.
3. The federal debt represents the aggregate of which factor over time?
A. rising interest rates
B. periods of structural unemployment
C. unpaid budget deficits
D. competitive devaluations of currency
Answers
This refers to the total amount of money that the federal government owes to creditors, including individuals, businesses, and foreign governments. It is primarily the result of unpaid budget deficits, which occur when the government spends more money than it collects in revenue. The federal debt can increase over time due to interest charges on the outstanding debt, as well as additional deficits in future years. Rising interest rates, periods of structural unemployment, and competitive devaluations of currency can all have an impact on the economy and government finances, but they do not directly contribute to the federal debt.
The Federal Reserve can change the discount rate, which is the interest rate at which banks can borrow from the Fed, to influence the borrowing behavior of banks. If the Fed lowers the discount rate, it becomes cheaper for banks to borrow money, which can lead to increased lending activity and economic growth. Conversely, if the Fed raises the discount rate, it becomes more expensive for banks to borrow money, which can decrease lending activity and slow down economic growth.
A marginal tax on sellers of a good will increase the costs of production, leading to a decrease in supply. This means that sellers will produce and offer less of the good at any given price, which will shift the supply curve to the left.
Leran more about federal debt on
https://brainly.com/question/14080872
#SPJ1
PLs solveg g g g g g g g g g g g

Answers

Answer:
4°=1
g g g g g g g g g g
Step-by-step explanation:
Please help !! 10 pts!!!!

Answers
Y = 8000/1000= 8
Y= 8*20
Y= 160
Which calculation will ALWAYS give a result greater than 1? 89 × a number less than 1 7 × a number less than 1 125 − a fraction less than 25 37 + a fraction less than 12
Answers
Answer:
The answer is "Option C".
Step-by-step explanation:
Please find the correct question in the attached file.
\(\to 1 \frac{2}{5} = \frac{7}{5} \\\\let \\ \to \frac{7}{5} =1.4\\\\\to \frac{2}{5}= 0.4\\\\\to 1.4- 0.4\\\\ \to 1\\\)
Its outcome is 1.4 if we subtract from 0.4. However, a fraction of less than 2/5 may be deducted. This means that the outcome still exceeds 1, that's why choice C is correct.
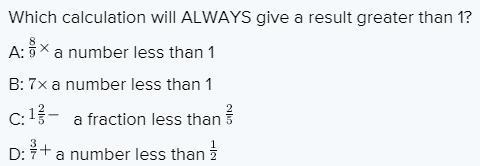
BRAINLIEST IF RIGHT FOR SURE
the difference between a number is 12 is 30
show steps brainly if correct
Answers
Answer:
18
X + 12 = 30
-12. -12. Subtract 12
X = 18. Answer
Answer:
42
Step-by-step explanation:
Slope is -4, and (3, 4) is on the line.
Answers
What is a slope in math?
The slope of a line is a measure of its steepness. Mathematically, slope is calculated as "rise over run" (change in y divided by change in x).
Whenever the equation of a line is written in the form y = mx + b, it is called the slope-intercept form of the equation. The m is the slope of the line. And b is the b in the point that is the y-intercept (0, b). For example, for the equation y = 3x – 7, the slope is 3, and the y-intercept is (0, −7).
To find the correct answer, we need to look at the formula for a straight line: y=mx+b where m= the slope of the line and b= the y intercept. We know from the problem that the slope must be equal to -4, leaving us with y= -4x +b. From here you can substitute the given point in the equation and solve for b.
-3= -4(4) +b
-3= -16+b
+16 +16
13= b
This tells us that b=13, now we simply substitute that into the formula.
The solution to your question is y=-4x+13
To learn more about slope visit:
https://brainly.com/question/3605446
#SPJ1
Problem Solving A London airport is 200 miles from Manchester airport. A plane leaves Manchester airport at 10 am to fly to the London airport. The plane flies at an average speed of 120 mph. What time does the plane arrive at the London airport?
Answers
The time the plane arrives at the London airport from the airport in Manchester, found using the kinematic equation for speed, and the conversion of the units from hours to minutes is 11:40 a.m.
What are the kinematic equations of motion?The kinematic equations describe the motion of an object that moves with constant acceleration.
Distance from the London airport to the Manchester airport, D = 200 miles
The average speed of the plane, v = 120 mph
Time the plane leaves Manchester airport = 10 a.m.
The kinematic equation that can be used to find the time of flight is presented as follows;
\(Speed, \, v = \dfrac{Distance, \, D }{Time, \, t}\)
Therefore;
\(t = \dfrac{D}{v}\)
The time of flight is therefore;
\(t = \dfrac{200}{120} = \dfrac{5}{3} = 1\dfrac{2}{3}\)
The time of flight is \(1\frac{2}{3}\) hours or 5/3 hours which in minutes is therefore:
\(t = \dfrac{5}{3} \, hr \times 60 \, min/hr= 100 \, min\)
100 minutes = 1 hour 40 minutesThe time of arrival is 10 a.m. + 1 hour 40 minutes = 11:40 a.m.
Learn more about the kinematic equations of motion here:
https://brainly.com/question/29580588
#SPJ1
The task should be the equivalent of approximately 500 words - or 1-3 pages at 11pt fontsize including examples, well set out equations, diagrams etc. It should be understandable to another student enrolled in this subject and include at least 3 references. Choose 1 of the following topics for investigation. Option 1 - Basics of Group Theory i. Learn the basics of what a 'group' is in group theory and provide a brief introduction in your own words. ii. Explain how group theory and some related concepts (e.g., Fields, Rings) relate to topics covered in SIT292 and provide original examples demonstrating fulfillment of properties, how the theory is useful etc. iii. Give an example of how the theory is applied in a different context or with a different mathematical structure, e.g. Dihedral groups in group theory or abstract examples of fields. Option 2 - Matrix Decompositions i. Learn how to perform either (choose one only) (a) Singular value decomposition, (b) QR decomposition or (c) QZ decomposition (generalised Schur decomposition - for real matrices), and provide a brief introduction in your own words. You can find basic descriptions of each type under the 'Matrix decomposition' Wikipedia entry, however you will need to find resources that go into more detail and provide better explanation. ii. Explain how the decomposition is useful in the context of linear algebra, and relate to specific topics covered in SIT292. iii. Work through an original example with annotation and explanation to help demonstrate how the method can be used.
Answers
Group theory is a branch of mathematics that studies the properties and structures of groups. It provides a framework for understanding symmetry, transformations, and patterns in various mathematical and scientific disciplines.
Group theory is a mathematical concept that explores the properties of groups. In mathematics, a group is a set of elements combined with an operation that satisfies specific conditions.
These conditions include closure (the operation performed on two elements of the group results in another element of the group), associativity (the order in which operations are performed does not affect the outcome), identity (there exists an element that does not change other elements when combined with them), and inverse (every element has an inverse element that, when combined, yields the identity element).
Groups have applications in many areas, including abstract algebra, geometry, physics, and computer science. In the context of linear algebra, group theory is particularly relevant.
The study of matrices and their operations involves understanding groups and their properties. For example, matrix multiplication exhibits the closure and associativity properties of groups. By applying group theory, we can analyze the behavior of matrices and identify patterns and symmetries.
Moreover, group theory connects to other mathematical concepts such as fields and rings. Fields are mathematical structures that include operations of addition, subtraction, multiplication, and division, while rings involve operations of addition and multiplication.
By studying the relationships between groups, fields, and rings, we can deepen our understanding of algebraic structures and their applications.
To illustrate the usefulness of group theory, consider the example of dihedral groups. Dihedral groups are a specific type of group that represents symmetries of regular polygons.
By applying group theory to dihedral groups, we can analyze the rotational and reflective symmetries of polygons, which have implications in geometry, crystallography, and other areas.
Learn more about Scientific disciplines
brainly.com/question/32667067
#SPJ11
Curtis Corporation reports net income for 20X9 of $150,000.00. Curtis Corporation had (1 point)
outstanding for all of 20X9 10,000 shares of cumulative $50.00 par, 10 percent preferred stock.
Curtis Corporation had outstanding for all of 20x9 75,000 shares of $10.00 par common stock.
Earnings per share is
O $1.20.
O $10.00
O $1.33.
O $2.00
Answers
Answer: $1.33.
Step-by-step explanation:
Earnings per share = (Net income - Preferred dividends) / Common shares outstanding
Preferred dividends = 10,000 shares * 50 * 10%
= $50,000
Earnings per share = (150,000 - 50,000) / 75,000
= $1.33
Lines a and b are parallel. What is the measure of angle s?
S= Enter your answer in the box.

Answers
Answer:
Step-by-step explanation:
t = 158 Corresponding angles
t + s = 180 They are supplementary angles
158 + s = 180 Subtract 158 from both sides
s = 180 - 158
s = 22
As a note, all angles in this situation are either 158 or 22.
What is the value of b in the equation y = mx + b for the line shown on the
graph above?

Answers
Answer:
-1
Step-by-step explanation:
the line crosses y at -1
In the form of a simple equation, what is the relationship between the number of address lines A on a decoder and its number of output lines Q? If a multiplexer has 4 address lines, how many output bits would it have?
Answers
The relationship between the number of address lines A on a decoder and its number of output lines Q is :
Q = 2^A
A multiplexer has 4 address lines, 1 output bit.
Binary Decoders are another type of digital logic device that has inputs of 2-bit, 3-bit or 4-bit codes depending upon the number of data input lines, so a decoder that has a set of two or more bits will be defined as having an n-bit code, and therefore it will be possible to represent 2n possible values. Thus, a decoder generally decodes a binary value into a non-binary one by setting exactly one of its n outputs to logic “1”.
The relationship between the number of address lines A on a decoder and its number of output lines Q is :
Q = 2^A
How is the number of select lines determined for a multiplexer?The number of select lines for a multiplexer is determined by the number of input lines, where the select lines are equal to the base-2 logarithm of the number of input lines. For example, a 16-input multiplexer requires four select lines because 2^4 = 16.
If a multiplexer has 4 address lines, 1 output bit.
Learn more about Decoders at:
https://brainly.com/question/30436042
#SPJ4
When James has five apples and he gives Aliya one apple how many apples does he have left
Answers
Answer: He has 4 apples left.
Step-by-step explanation:
5-1=4
(hope this helps)
Answer:4
Step-by-step explanation: James had 5 apples which later he gave one to aliya so 5-1 is 4
The time between calls to a corporate office is exponentially distributed with a mean of 10 minutes. (a) What is the probability that there are more than three calls in one-half hour? (b) What is the probability that there are no calls within one-half hour? (c) Determine x such that the probability that there are no calls within x hours is 0.01 (d) What is the probability that there are no calls within a two-hour interval? (e) If four no overlapping one-half-hour intervals are selected, what is the probability that none of these intervals contains any call?
Answers
the probability that none of the four non-overlapping one-half hour intervals contains any call is approximately 0.00000614.
(a) The probability of having more than three calls in one-half hour can be calculated using the exponential distribution. Since the mean of the exponential distribution is 10 minutes, the rate parameter (λ) can be calculated as λ = 1/mean = 1/10 = 0.1 calls per minute.
To find the probability of having more than three calls in one-half hour (30 minutes), we need to calculate the cumulative distribution function (CDF) of the exponential distribution up to three calls and subtract it from 1.
P(X > 3) = 1 - P(X ≤ 3)
= 1 - (1 - e^(-λt)) [where t is the time duration in minutes]
= 1 - (1 - e^(-0.1 * 30))
= 1 - (1 - e^(-3))
= 1 - (1 - 0.049787)
= 0.049787
Therefore, the probability of having more than three calls in one-half hour is approximately 0.0498 or 4.98%.
(b) The probability of having no calls within one-half hour can be calculated using the exponential distribution as well.
P(X = 0) = e^(-λt) [where t is the time duration in minutes]
= e^(-0.1 * 30)
= e^(-3)
≈ 0.049787
Therefore, the probability of having no calls within one-half hour is approximately 0.0498 or 4.98%.
(c) To determine x such that the probability of having no calls within x hours is 0.01, we need to solve the exponential distribution equation.
0.01 = e^(-0.1 * x * 60)
Taking the natural logarithm of both sides, we get:
ln(0.01) = -0.1 * x * 60
x = ln(0.01) / (-0.1 * 60)
≈ 230.26
Therefore, x is approximately 230.26 hours.
(d) The probability of having no calls within a two-hour interval can be calculated using the exponential distribution.
P(X = 0) = e^(-λt) [where t is the time duration in minutes]
= e^(-0.1 * 120)
= e^(-12)
≈ 6.14e-06
Therefore, the probability of having no calls within a two-hour interval is approximately 6.14e-06 or 0.00000614.
(e) If four non-overlapping one-half hour intervals are selected, the probability that none of these intervals contains any call can be calculated by multiplying the individual probabilities of no calls in each interval.
P(no calls in one interval) = e^(-0.1 * 30)
≈ 0.0498
P(no calls in all four intervals) = (0.0498)^4
≈ 6.14e-06
Therefore, the probability that none of the four intervals contains any call is approximately 6.14e-06 or 0.00000614.
Conclusion: In this scenario with exponentially distributed call intervals, we calculated probabilities for different cases. The probability of having more than three calls in one-half hour is approximately 4.98%, while the probability of having no calls within one-half hour is also approximately 4.98%. We found that x is approximately 230.26 hours for a 0.01 probability of having no calls within x hours. The probability of having no calls within a two-hour interval is approximately 0
.00000614. Lastly, the probability that none of the four non-overlapping one-half hour intervals contains any call is approximately 0.00000614.
To know more about probability follow the link:
https://brainly.com/question/23417919
#SPJ11
in example 4.4 suppose that it has rained neither yesterday nor the day before yesterday. what is the probability that it will rain tomorrow?
Answers
The probability of rain tomorrow is the same regardless of whether it has rained in the past two days or not. Therefore, we cannot use the given information to make a prediction about the weather tomorrow.
In example 4.4, we are given a situation where it has not rained in the past two days. The question asks for the probability of rain tomorrow. This type of question falls under the category of conditional probability. In conditional probability, we find the probability of an event given that another event has already occurred.
To solve this problem, we can use Bayes' theorem. Bayes' theorem states that the probability of an event A given that event B has occurred is equal to the probability of event B given that event A has occurred multiplied by the probability of event A divided by the probability of event B.
Let us define the events in this problem as follows:
A = It will rain tomorrow
B = It has not rained in the past two days
Using the given information, we know that P(B) = 0.75 (since there are four possible outcomes: rain yesterday, rain day before yesterday, rain both days, no rain both days, and we are given that the latter has occurred). We need to find P(A|B).
To find P(A|B), we need to find P(B|A), which is the probability that it has not rained in the past two days given that it will rain tomorrow. Since we do not have any information about the relationship between these two events, we can assume that they are independent.
Therefore, P(B|A) = P(B) = 0.75
Now, we can use Bayes' theorem to find P(A|B):
P(A|B) = P(B|A) * P(A) / P(B)
P(A|B) = 0.75 * P(A) / 0.75
P(A|B) = P(A)
This means that the probability of rain tomorrow is the same regardless of whether it has rained in the past two days or not. Therefore, we cannot use the given information to make a prediction about the weather tomorrow.
for more questions on probability
https://brainly.com/question/24756209
#SPJ11
What is the product? StartFraction 4 k + 2 Over k squared minus 4 EndFraction times StartFraction k minus 2 Over 2 k + 1 EndFraction StartFraction 4 Over 2 k + 1 EndFraction StartFraction 2 Over k minus 2 EndFraction StartFraction 2 Over 2 k + 1 EndFraction StartFraction 2 Over k + 2 EndFraction
Answers
Answer:
\(\frac{2}{k+2}\)
Step-by-step explanation:
Given the expression:
\(\frac{4k+2}{k^2-4} * \frac{k-2}{2k+1}\)
We are to find the product as shown:
\(= \frac{4k+2}{k^2-4} * \frac{k-2}{2k+1}\\\\= \frac{2(2k+1)}{k^2-2^2} * \frac{k-2}{2k+1}\\\\= \frac{2(2k+1)}{(k-2)(k+2)} * \frac{k-2}{2k+1}\\\\= \frac{2}{k+2} * 1\\\\= \frac{2}{k+2}\)
Hence the required function is \(\frac{2}{k+2}\)
d. StartFraction 2 Over k + 2 EndFraction
aka
d. 2/k+2
find an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is 5xy. (note: start your answer with y
Answers
The equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is y = (5/2) * x^2y + 1. This equation represents a curve where the y-coordinate is a function of the x-coordinate, satisfying the conditions.
To determine an equation of the curve that satisfies the conditions, we can integrate the slope function with respect to x to obtain the equation of the curve. Let's proceed with the calculations:
We have:
Point: (0, 1)
Slope: 5xy
We can start by integrating the slope function to find the equation of the curve:
∫(dy/dx) dx = ∫(5xy) dx
Integrating both sides:
∫dy = ∫(5xy) dx
Integrating with respect to y on the left side gives us:
y = ∫(5xy) dx
To solve this integral, we treat y as a constant and integrate with respect to x:
y = 5∫(xy) dx
Using the power rule of integration, where the integral of x^n dx is (1/(n+1)) * x^(n+1), we integrate x with respect to x and get:
y = 5 * (1/2) * x^2y + C
Applying the initial condition (0, 1), we substitute x = 0 and y = 1 into the equation to find the value of the constant C:
1 = 5 * (1/2) * (0)^2 * 1 + C
1 = C
Therefore, the equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is:
y = 5 * (1/2) * x^2y + 1
Simplifying further, we have:
y = (5/2) * x^2y + 1
To know more about equation of the curve refer here:
https://brainly.com/question/31467851#
#SPJ11
Can anyone explain why the answer is B? Tyyy

Answers
Answer:
B. 4.09 cm²
Step-by-step explanation:
Let point O be the center of the circle.
As the center of the circle is the midpoint of the diameter, place point O midway between P and R.
Therefore, line segments OP and OQ are the radii of the circle.
As the radius (r) of a circle is half its diameter, r = OP = OQ = 5 cm.
As OP = OQ, triangle POQ is an isosceles triangle, where its apex angle is the central angle θ.
To calculate the shaded area, we need to subtract the area of the isosceles triangle POQ from the area of the sector of the circle POQ.
To do this, we first need to find the measure of angle θ by using the chord length formula:
\(\boxed{\begin{minipage}{5.8 cm}\underline{Chord length formula}\\\\Chord length $=2r\sin\left(\dfrac{\theta}{2}\right)$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the central angle.\\\end{minipage}}\)
Given the radius is 5 cm and the chord length PQ is 6 cm.
\(\begin{aligned}\textsf{Chord length}&=2r\sin\left(\dfrac{\theta}{2}\right)\\\\\implies 6&=2(5)\sin \left(\dfrac{\theta}{2}\right)\\\\6&=10\sin \left(\dfrac{\theta}{2}\right)\\\\\dfrac{3}{5}&=\sin \left(\dfrac{\theta}{2}\right)\\\\\dfrac{\theta}{2}&=\sin^{-1} \left(\dfrac{3}{5}\right)\\\\\theta&=2\sin^{-1} \left(\dfrac{3}{5}\right)\\\\\theta&=73.73979529...^{\circ}\end{aligned}\)
Therefore, the measure of angle θ is 73.73979529...°.
Next, we need to find the area of the sector POQ.
To do this, use the formula for the area of a sector.
\(\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\left(\dfrac{\theta}{360^{\circ}}\right) \pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in degrees.\\\end{minipage}}\)
Substitute θ = 73.73979529...° and r = 5 into the formula:
\(\begin{aligned}\textsf{Area of section $POQ$}&=\left(\dfrac{73.73979529...^{\circ}}{360^{\circ}}\right) \pi (5)^2\\\\&=0.20483... \cdot 25\pi\\\\&=16.0875277...\; \sf cm^2\end{aligned}\)
Therefore, the area of sector POQ is 16.0875277... cm².
Now we need to find the area of the isosceles triangle POQ.
To do this, we can use the area of an isosceles triangle formula.
\(\boxed{\begin{minipage}{6.7 cm}\underline{Area of an isosceles triangle}\\\\$A=\dfrac{1}{2}b\sqrt{a^2-\dfrac{b^2}{4}}$\\\\where:\\ \phantom{ww}$\bullet$ $a$ is the leg (congruent sides). \\ \phantom{ww}$\bullet$ $b$ is the base (side opposite the apex).\\\end{minipage}}\)
The base of triangle POQ is the chord, so b = 6 cm.
The legs are the radii of the circle, so a = 5 cm.
Substitute these values into the formula:
\(\begin{aligned}\textsf{Area of $\triangle POQ$}&=\dfrac{1}{2}(6)\sqrt{5^2-\dfrac{6^2}{4}}\\\\ &=3\sqrt{25-9}\\\\&=3\sqrt{16}\\\\&=3\cdot 4\\\\&=12\; \sf cm^2\end{aligned}\)
So the area of the isosceles triangle POQ is 12 cm².
Finally, to calculate the shaded area, subtract the area of the isosceles triangle from the area of the sector:
\(\begin{aligned}\textsf{Shaded area}&=\textsf{Area of sector $POQ$}-\textsf{Area of $\triangle POQ$}\\\\&=16.0875277...-12\\\\&=4.0875277...\\\\&=4.09\; \sf cm^2\end{aligned}\)
Therefore, the area of the shaded region is 4.09 cm².

As you have seen, relativistic calculations usually involve the quantity When is appreciably greater than we must use relativistic formulas instead of Newtonian ones. For what speed (in terms of is the value of greater than (b) 10
greater than 1 ; (c) 100
greater than 1
Answers
The value of γ is greater than 1 for any v > 0, greater than 10 for v > 0.995c, and greater than 100 for v > 0.99995c.
To determine for what speed (in terms of c) the value of γ is greater than 1, 10, and 100, we'll use the formula for the Lorentz factor (γ):
γ = 1 / √(1 - v²/c²)
where v is the speed and
c is the speed of light.
(a) For γ > 1:
Since γ is always greater than 1 for any speed v greater than 0, we can say that γ is appreciably greater than 1 for any v > 0.
(b) For γ > 10:
We need to solve the equation 10 = 1 / √(1 - v²/c²) for v/c:
Squaring both sides, we get 100 = 1 / (1 - v²/c²).
Now, solve for v²/c²: v²/c² = 1 - 1/100 = 99/100.
So, v/c = √(99/100), which implies v > 0.995c for γ > 10.
(c) For γ > 100:
Similar to (b), solve the equation 100 = 1 / √(1 - v²/c²) for v/c:
Squaring both sides, we get 10000 = 1 / (1 - v²/c²).
Now, solve for v²/c²: v²/c² = 1 - 1/10000 = 9999/10000.
So, v/c = √(9999/10000), which implies v > 0.99995c for γ > 100.
To know more about "Speed" refer here:
https://brainly.com/question/8025703#
#SPJ11
How many 1/8's are in 1/2 inch?
A.
8.
B
6
c
4
D
3
Answers
Answer:
C
Step-by-step explanation:
8) Write the equation in standard or y=mx+b form

Answers
The equation of the line in slope-intercept form is y = -2x + 1/4
Equation of a lineA line is the shortest distance between two points. The standard equation of a line is expressed as y = mx + b
where:
m is the slope
b is the intercept
Using the coordinate points (0, 1/4) and (-1, 2 1/4)
Determine the slope
Slope = (2 1/4 - 1/4)/-1
Slope = 8/-4
slope = -2
Since the y-intercept is the point where x = 0, hence the y-intercept is 1/4
Determine the equation
y = -2x + 1/4
Hence the equation of the line in slope-intercept form is y = -2x + 1/4
Learn more on equation of a line here: https://brainly.com/question/13763238
#SPJ1
Please helppppppppppppppppppp :) .

Answers
Answer and Step-by-step explanation:
I think this is the correct answer (in picture):
This is because you can either get Heads or Tails, so once you flip it once, you just flip it again and you will get either heads or tails.
#teamtrees #PAW (Plant And Water)

Is (x+1) a factor of f(x) = x^4 - 3x^3 + 2x - 2?

Answers
Answer:
\(\text{Yes}\)Explanation:
According to the factor theorem, if we set x+1 to zero, the substitute the x value into the polynomial, if we get a value of zero, then x+1 is a factor of the polynomial, otherwise, it is not
We start by setting x+1 to zero:
\(\begin{gathered} \text{ x+1 = 0} \\ x\text{ = -1} \end{gathered}\)Substitute -1 into the polynomial:
\(\begin{gathered} f(-1)=-1^4-3(-1)^3+2(-1)-2 \\ f(-1)\text{ = 1+3-2-2} \\ f(-1)\text{ = 4-4} \\ f(-1)\text{ = 0} \end{gathered}\)This shows that (x+1) is a factor of the polynomial
5(-7k+4d) Use k=-7 and d=4
Simplified is??
Answers
Answer:
325
Step-by-step explanation:
k = -7
d=4
5(-7k + 4d)
5(-7(-7) + 4(4))
5(49 + 16)
325
please give brainliest I need it to level up
A school playground is in the shape of a parallelogram. The base of the parallelogram is six times as long as the height. The area of the playground is 5040 square feet. What is the length of the longer side of the playground? Round to the nearest foot.Hint : Use A = bh.
Answers
Let x be the height, we know that the base is six times as long, this means that the base can be express as:
\(b=6x\)Now, thas we know the height and the base we plug them in the equation for the area and solve for x:
\(\begin{gathered} 6x\cdot x=5040 \\ 6x^2=5040 \\ x^2=\frac{5040}{6} \\ x^2=840 \\ x=\sqrt{840} \\ x\approx28.98 \end{gathered}\)Now, that we know the value of x we can calculate the length of the base (which is the longer side of the playground):
\(6(28.98)=173.88\)Therefore, the length of the longer side is 173.88 ft
x=3y+1
2x+4y=12
Solve each system by substitution
Answers
The required values are :
\(\qquad \sf \dashrightarrow \:x = 4\)
and
\(\qquad \sf \dashrightarrow \:y = 1\)
Check the attachment for solution ~
➖➖➖➖➖➖➖➖➖➖➖➖➖➖➖➖➖

Stacy has a spinner and a number cube after spinning and rolling the number cube she will add two number what is the probability that the sum of the numbers from the spinner and number cube will be 3 or 4
Answers
Complete question :
Stacy has a spinner (1 - 4) and a number cube (1 - 6) after spinning and rolling the number cube she will add two number what is the probability that the sum of the numbers from the spinner and number cube will be 3 or 4
Answer:
5 /24
Step-by-step explanation:
The sample space for the sun of the outcome of the spinner and rolled number cube ;
Sample space = total possible outcomes = 6 * 4 = 24
Required outcome = sum equals 3 or 4 = 5
P(obtaining a sum of 3 or 4) = required outcome / Total possible outcomes
P(obtaining a sum of 3 or 4) = 5 /24

Marking BRAINLYEST need help ASAP
In the diagram, the measures of 3 and 6 are 50°. The measure of 5 is
130°. Are lines cand d parallel?
1/2
3 4
d
5
6
7
8
O A. Yes, because 5 and 6 are supplementary
B. No, because 6 and 5 are not congruent.
O C. Yes, because 3 and 6 are congruent.
D. No, because 3 and 5 are not supplementary

Answers
Answer:
c
Step-by-step explanation:
The solution is, (c) Yes, because angle 3 and angle 6 are congruent.
What is an angle?In Plane Geometry, a figure which is formed by two rays or lines that shares a common endpoint is called an angle. The two rays are called the sides of an angle, and the common endpoint is called the vertex.
here, we have,
given that,
Angles 3 and 6 are "alternate interior" angles. When those angles are congruent, as these are, then the lines crossed by the transversal are parallel.
we have,
We expect angles 5 and 6 to be supplementary because they are a linear pair.
That fact says nothing about the relationship of line d to line c.
Hence, The solution is, (c) Yes, because angle 3 and angle 6 are congruent.
To learn more on angle click:
brainly.com/question/28451077
#SPJ5
2 apples cost 2 dabloons.
How much does 1 apple cost
Answers
True or false: Weight which is less than 85% of what is considered normal for age and height is a main characteristic of bulimia nervosa.
Answers
The statement refers to anorexia nervosa and not bulimia nervosa. Therefore, the statement is FALSE.
What is Bulimia Nervosa?Bulimia nervosa can be described as an eating disorder whereby an individual eats a lot of food without control and afterwards try to purge themselves to get rid of extra calories.
On the other hand, a similar eating disorder that is characterized with fear of being overfat but also follows with abnormal excessive weight loss is called anorexia nervosa.
Therefore, the statement refers to anorexia nervosa and not bulimia nervosa. Therefore, the statement is FALSE.
Learn more about bulimia nervosa on:
https://brainly.com/question/7061676