Re-write the quadratic function below in Standard Form y = −2(x−6)(x−2)
Answers
Answer:
THE answer is y= -2x²+16x-24
Step-by-step explanation:
OK, so the standard form for an equation is ax²+bx+c
When you look at the equation we see that there is a -2 all by itself so we need too bring it within the parenthesis, so we'll distribute it..... so now instead of 2(x-6), we have -2x-12..........Why? because (2 times x is 2x and 2 times six is 12)
next when you write it ALL out, you get (-2x+12)(x-2) now we need to put this in the standard form by using the FOIL method
F- first O-outer I-inner L-last..... so multiplying the First from both equations we get -2x², Outer is -2x times -2 which is 4 because two negatives make a positive, Inner is 12 times x which is 12x, Last is 12 times -2 whchis -24. Put them all together and you get. 2x²+12x+4x- 24, now we combine like terms (in bold) and we get -2x²+16x-24. Look at the standard form i gave above and see how the final answer matches
-2x²+16x-24
ax² +bx + c
Related Questions
x reduced by 5 is less than 12
Answers
Answer:
x < 17
Step-by-step explanation:
im guessing its simplify the equation.
just add 5 to both sides and positive 5 cancels out the subtract five.
twelve + five is 17.
Leah can run 720 yards in 4.5 minutes. How many yards can she run in 2 minutes at the same rate?
A. 350
B. 320
C. 160
D. 110
Answers
Leah can run 320 yards in 2 minutes at the same rate as she can run 720 yards in 4.5 minutes. The correct option is B. 320.
To find out how many yards Leah can run in 2 minutes at the same rate, we can use the concept of proportionality.
Let's set up a proportion based on the information given:
720 yards / 4.5 minutes = x yards / 2 minutes
To find the value of x, we can cross-multiply:
4.5 minutes × x yards = 720 yards × 2 minutes
Now, divide both sides by 4.5 to solve for x:
x yards = (720 yards × 2 minutes) / 4.5 minutes
x yards = 320 yards
So, Leah can run 320 yards in 2 minutes at the same rate.
The correct answer is B. 320.
To know more about proportionality:
https://brainly.com/question/8598338
#SPJ2
Please help me
Find the values of x and y

Answers
(12x +15)°=75° .…(शिर्षभिमुख कोण भएर)
or, 12x+15=75
or, 12x=75-15
or, 12x=60
or, x=60÷12
or, x=5
(6y-27)°=105° .…(शिर्षभिमुख कोण भएर)
or, 6y-27=105
or, 6y=105+27
or, 6y=132
or, y=132÷6
or, y=22
Calculate the surface area of the cylinder below the diameter of the cylinder is 14 cm.
(Don’t mind the -1)

Answers
the surface area is the sum of the circle at the top, the circle at the bottom and the rectangle that "covers the cylinder", like the label of a can if that makes sense.
the surface area for each circle is
S= π × r²
where r is the radius, this is diameter/2
the surface area for the rectangle is
S= b × h
where the base is the diameter and the height comes from this formula
hyp² = op² + adj²
because you have a right triangle where your hypotenuse is 20cm, your opposite cathetus is the one you need because is theheight of the cylinder , and the adjacent cathetus is the diameter
hope this helps, the answer should be 507.68cm²
+please help i dont know how to solve this

Answers
Answer:
thee answer is 3375ft
Step-by-step explanation:
Volume =length x width x height
V = 15ft x 15ft x 15ft
=3375 ft
can I please get brainly
Find the particular solution of the differential equation that satisfies the initial condition. (Enter your solution as an equation.)
Differential Equation:
dT+k(T-60)dt=0
Initial Condition:
T=139 when t=0
Answers
Answer:
T = 79e^(-kt) +60
Step-by-step explanation:
You want the particular solution to the differential equation ...
dT +k(T -60)dt = 0 . . . . T(0) = 139
SolutionThis is a separable differential equation, so we can solve it by separating the variables and integrating each side:
\(\dfrac{dT}{T-60}=-k\,dt\\\\\displaystyle \int{\dfrac{dT}{T-60}}=\int{-k}\,dt\\\\\ln{(T-60)}=-kt+C\\\\T-60=e^{-kt+C}=Ce^{-kt}\qquad\text{take antilogs; values of $C$ are different}\)
Applying the initial condition, we have ...
139 -60 = C = 79
Then the particular solution is ...
\(\boxed{T=79e^{-kt}+60}\)
Determine the truth value of each of the following complex statements.
Circle your answer or put it in red. (NOTE: LET A, B, C BE TRUE AND X, Y, Z BE FALSE)
3. B. Z 4. Xv-Y
5. CvZ 6. B-Z 7. (A v B)Z 8. (AZ) 9. B v (Y - A) 10. A) -(Z v-Y) 11.( AY) v (-Z.C) 12. -X v-B) (~Y v A) 13. (Y » C)-(B3-X) 14.(C =~A) v (Y = Z) 15.-(AC)(-XB) 16.( AY). (-Z.C) 17.-[( AZ) = (-C •-X)] 18. ~~[( AZ) = (-C •-X)] 19.-(A.-Z) v (Y = Z) 20. A. A
Answers
The truth values for the given complex statements are:
3. False
4. False
5. False
6. True
7. False
8. Undefined
9. True
10. True
11. True
12. False
13. True
14. True
15. True
16. False
17. True
18. False
19. True
20. False
To determine the truth value of each complex statement, we'll use the given truth values:
A = True
B = True
C = True
X = False
Y = False
Z = False
Let's evaluate each statement:
3. B • Z
B = True, Z = False
Truth value = True • False = False
4. X V Y
X = False, Y = False
Truth value = False V False = False
5. ~C v Z
C = True, Z = False
Truth value = ~True v False = False v False = False
6. B - Z
B = True, Z = False
Truth value = True - False = True
7. (A v B) Z
A = True, B = True, Z = False
Truth value = (True v True) • False = True • False = False
8. ~(THIS)
"THIS" is not defined, so we cannot determine its truth value.
9. B v (Y • A)
B = True, Y = False, A = True
Truth value = True v (False • True) = True v False = True
10. A • (Z v ~Y)
A = True, Z = False, Y = False
Truth value = True • (False v ~False) = True • (False v True) = True • True = True
11. (A • Y) v (~Z • C)
A = True, Y = False, Z = False, C = True
Truth value = (True • False) v (~False • True) = False v True = True
12. (X v ~B) • (~Y v A)
X = False, B = True, Y = False, A = True
Truth value = (False v ~True) • (~False v True) = False • True = False
13. (Y • C) ~ (B • ~X)
Y = False, C = True, B = True, X = False
Truth value = (False • True) ~ (True • ~False) = False ~ True = True
14. (C • A) v (Y = Z)
C = True, A = True, Y = False, Z = False
Truth value = (True • True) v (False = False) = True v True = True
15. (A • C) (~X • B)
A = True, C = True, X = False, B = True
Truth value = (True • True) (~False • True) = True • True = True
16. (A • Y) (~Z • C)
A = True, Y = False, Z = False, C = True
Truth value = (True • False) (~False • True) = False • True = False
17. ~[(A • Z) (~C • ~X)]
A = True, Z = False, C = True, X = False
Truth value = ~(True • False) (~True • ~False) = ~False • True = True
18. [(A • Z) (~C • ~X)]
A = True, Z = False, C = True, X = False
Truth value = (True • False) (~True • ~False) = False • True = False
19. (A • Z) v (Y = Z)
A = True, Z = False, Y = False
Truth value = (True • False) v (False = False) = False v True = True
20. A • ~A
A = True
Truth value = True • ~True = True • False = False
Therefore, the truth values for the given complex statements are:
3. False
4. False
5. False
6. True
7. False
8. Undefined
9. True
10. True
11. True
12. False
13. True
14. True
15. True
16. False
17. True
18. False
19. True
20. False
Learn more about Truth Value at
brainly.com/question/29137731
#SPJ4
Help me exercise 1 and 2

Answers
Answer:
it is so hard as I am studying in just grade 8
HELP QUICK, I WILL DO ANYTHING, I WILL GIVE BRAINLIEST AND 15 POINTS HELP QUICK
I need help with writing an expression for this figure.
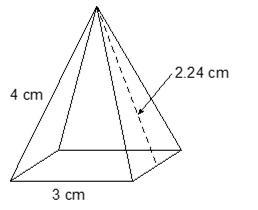
Answers
Answer:
2bs + b^2, this is the equation to find the surface area. B is base length and s is slant height.
Step-by-step explanation:
please help will mark Brainliest

Answers
Answer:
9 - 4x = 9
Step-by-step explanation:
Hope it Helps
In a 2012 interview with CBS News, Tom Hanks said that "80% of the population are really great, caring people who will help you and tell the truth. And I think 20% of the population are crooks and liars." A new lie detector suit has been tested and was sho
wn to correctly identify truthful people 88.9% of the time and correctly identify liars 75.6% of the time. A positive test is one in which the person is identified as a liar and a negative test is one in which the person is identified as truthful. Sometimes, the test suggests that a truthful person is a liar (a "false positive"); other times, the test indicates that a liar is being truthful (a "false negative"). Assume that Tom Hanks and the company that makes the lie detector suit are telling the truth. A randomly selected person from the population tests positive for being a liar. Find the probability that this person is a liar.
Answers
The probability that a randomly selected person from the population, who tests positive for being a liar, is indeed a liar is approximately 0.63 or 63%.
To find the probability that a randomly selected person who tests positive for being a liar is indeed a liar, we can use Bayes' theorem. Let's define the following events:
A: The person is a liar.
B: The person tests positive for being a liar.
We are given the following probabilities:
P(A) = 0.20 (Tom Hanks' statement that 20% of the population are liars)
P(B|A) = 0.756 (the lie detector correctly identifies a liar)
P(B|not A) = 0.111 (the lie detector incorrectly identifies a truthful person as a liar)
We want to find P(A|B), the probability that the person is a liar given that they tested positive. According to Bayes' theorem, we have:
P(A|B) = (P(B|A) * P(A)) / P(B)
To find P(B), we can use the law of total probability:
P(B) = P(B|A) * P(A) + P(B|not A) * P(not A)
Since we know that P(not A) = 1 - P(A), we can substitute this into the equation:
P(B) = P(B|A) * P(A) + P(B|not A) * (1 - P(A))
Plugging in the given probabilities, we have:
P(B) = (0.756 * 0.20) + (0.111 * 0.80) = 0.1512 + 0.0888 = 0.24
Now we can substitute this back into the equation for P(A|B):
P(A|B) = (0.756 * 0.20) / 0.24 = 0.1512 / 0.24 = 0.63
Therefore, the probability that a randomly selected person from the population, who tests positive for being a liar, is indeed a liar is approximately 0.63 or 63%.
For more such questions on probability
https://brainly.com/question/31828911
#SPJ8
adding and subtracting fractions with whole numbers
Answers
The steps for adding and subtracting fractions with whole numbers:
- Write the whole number in the form of a fraction.
- Convert the fractions to like fractions.
- Add/Subtract the numerators while the denominator remains the same.
We know that the fraction is used to represent the portion or part of the whole thing.
The fraction has two parts: numerator and denominator.
The top part of fraction is numerator and the bottom part of fraction is denominator.
consider a fraction 1/8.
Here, numerator is 1, denominator is 8
When certain thing is divided into 8 equal parts then each part of is represented by fraction1/8
In case of adding and subtracting fractions with whole numbers:
Let us assume that 'a' represents the whole number and \(\frac{x}{y}\) be fraction
First we write the whole number in the form of a fraction.
So, a = \(a = \frac{a}{1}\)
Now we find the LCM of the denominators of fractions \(\frac{a}{1} ,\frac{x}{y}\) and then convert the given fractions to like fractions.
Let m be the LCM of the denominators of fractions \(\frac{a}{1} ,\frac{x}{y}\)
So, the fractions becomes \(\frac{a}{m} ,\frac{x}{m}\)
Last we Add/Subtract the numerators while the denominator remains the same.
i.e., \(\frac{a\pm x}{m}\)
Learn more about fraction here:
brainly.com/question/24638688
#SPJ4
The complete question is:
How to add /subtract fractions with whole numbers?
4(0.5x - 3) = x - 0.25(12 - 8x)
Answers
Answer:
x = -9
Step-by-step explanation:
4(0.5x - 3) = x - 0.25(12 - 8x)
2x - 12 = x - 3 + 2x
2x - 12 = 3x - 3
2x = 3x + 9
-x = 9
x = -9
A gas mixture has a total pressure of 0.56 atm and consists of He and Ne. If the partial pressure of the He in the mixture os 0.27 atm. What is the partial pressure of the Ne in the mixture?
Answers
The partial pressure of the Ne in the mixture is 0.29 atm if the as mixture has a total pressure of 0.56 atm and consists of He and Ne.
What is Dalton's law?Dalton's law states that the total partial pressures of all the gases in a mixture of non-reacting gases at a constant temperature equal the pressure the mixture exerts.
We have:
A gas mixture has a total pressure of 0.56 atm and consists of He and Ne. If the partial pressure of the He in the mixture os 0.27 atm.
According to Dalton's law
Total pressure = partial pressure of He + Partial pressure of Ne
0.56 = 0.27 + P(Ne)
P(Ne) = 0.29 atm
Thus, the partial pressure of the Ne in the mixture is 0.29 atm if the as mixture has a total pressure of 0.56 atm and consists of He and Ne.
Learn more about the dalton law here:
https://brainly.com/question/14263053
#SPJ1
Sara has 16 red flowers and 24 yellow flowers. She wants to make bouquets with the same number of each color flower in each bouquet.
Part A: What is the greatest number of bouquets she can make?
(Include the numerical answer only.)
Answers
Answer:
8
Step-by-step explanation:
make 8 bouquets: Each bouquet will have 2 red flowers and 3 yellow flowers.
please solve both the parts because it's compulsory, I will give you thumbs up vote for this . Please use pumping lemma method . Let Σ={a,b}. For each k≥1, let C k
be the language consisting of all strings that contain an a exactly k places from the right-hand end. Thus C k
=Σ ∗
aΣ k−1
. Describe an NFA with k+1 states that recognizes C k
in terms of both a state diagram and a formal description.
Answers
The formal description for the NFA that recognizes Ck is as follows:
M = ({q₀, q₁, q₂, q₃,…qk}, Σ, δ, q₀, {qk}) where δ is the transition function defined as
δ(qi, a) = qi+1 if 0 ≤ i ≤ k-1, and δ(qk-j, a) = qk-j for 1 ≤ j ≤ k.
For Σ = {a, b} and k ≥ 1, let Ck be the language that consists of all the strings which contains an a exactly k places from the right-hand end.
That means, Ck = Σ*aΣk-1.
To get an NFA with k+1 states that recognizes Ck, follow these steps:
We can start by taking the NFA with (k+1) states,
where {q₀, q₁, q₂, q₃,…qk} are the set of states.
The transition diagram for the NFA is given below, which can be represented as (q₀, q₁, q₂, q₃, …qk)
q₀ ----> q₁ on aq₁ ----> q₂ on a or b.
Now, the loopback transitions start from the kth state in the following way:
qk ----> qk on a or bqk-1 ----> qk on a or bqk-2 ----> qk on a or bqk-3 ----> qk on a or bq2 ----> qk on a or bq1 ----> qk on a or b.
To be more precise, if k=3, the transition diagram will look like the following diagram.
Finally, the formal description for the NFA that recognizes Ck is as follows:
M = ({q₀, q₁, q₂, q₃,…qk}, Σ, δ, q₀, {qk}) where δ is the transition function defined as
δ(qi, a) = qi+1 if 0 ≤ i ≤ k-1, and δ(qk-j, a) = qk-j for 1 ≤ j ≤ k.
To know more about transition, visit:
https://brainly.com/question/14274301
#SPJ11
How to write 4.651 in expanded form with decimals?
Answers
Answer:
\(0.4651 \times {10}^{1} \)
Pro ) Find \( \frac{d y}{d x} \) from \( y=\ln x^{2}+\ln (x+3)-\ln (2 x+1) \)
Answers
To find (the derivative of \( y \) with respect to \( x \)) from the given function \( y = \ln(x^2) + \ln(x+3) - \ln(2x+1) \), we can apply the rules of logarithmic differentiation.
First, we can rewrite the function using logarithmic properties:
\(\( y = \ln(x^2) + \ln(x+3) - \ln(2x+1) = \ln(x^2(x+3)) - \ln(2x+1) \).\)
Now, using the rules of logarithmic differentiation, we can differentiate \( y \) with respect to \( x \) as follows:
\( \frac{dy}{dx} = \frac{1}{x^2(x+3)} \cdot (2x(x+3)) - \frac{1}{2x+1} \).
Simplifying further:
\(\( \frac{dy}{dx} = \frac{2x(x+3)}{x^2(x+3)} - \frac{1}{2x+1} \).\( \frac{dy}{dx} = \frac{2x^2 + 6x}{x^2(x+3)} - \frac{1}{2x+1} \).Thus, \( \frac{dy}{dx} = \frac{2x^2 + 6x}{x^2(x+3)} - \frac{1}{2x+1} \) is the derivative of \( y \) with respect to \( x \)\) for the given function.
Learn more about logarithmic differentiation here: brainly.com/question/14350001
#SPJ11
PLEASE HELP GIVING POINTS :))!!

Answers
Answer:
(3, 1)
Step-by-step explanation:
The coordinates of point B' after rotating segment AB 90° about point A will be (3, 1)
an internet company charges 500 pesos for the first 30 GB used in a month. every exceeding GB will then cost 30 but if the costumer reach a total of 50 GB and above, a flat rate of 1000 will be flat instead. write a piecewise function C(g) that represent the charge according to GB used?
Answers
Answer:
For first 30 GB, a fix payment of 500 Pesos, equation would be:
C(g) = 500(g⁰), note: g⁰ = 1, where g ≤ 30
It is also equal to C(g) = 500 when g ≤ 30.
For 30 GB to 49 GB, 30 pesos each GB will be charged, equation would be:
C(g) = 500 + 30(g-30)
C(g) = 500 + 30g - 90
C(g) = 30g + 410, where 30 < g < 50
For 50 GB and above, the equation will be:
C(g) = 1000(g⁰), where g ≥ 50
It is also equal to C(g) = 1000, when g ≥ 50.
2. suppose that a deck of 52 cards contains 26 red cards and 26 black cards (and assume the red cards are numbered 1 to 26, and so are the black cards). say we use the 52 cards to randomly distribute 13 cards each among two players (2 players receive 13 card each). a. how many ways are there to pass out 13 cards to each of the two players?
Answers
There are 5,148,644 ways to pass out 13 cards to each of the two players from a deck of 52 cards containing 26 red cards and 26 black cards, assuming that the distribution is random.
To distribute 13 cards each among two players from a deck of 52 cards containing 26 red cards and 26 black cards, we can use the formula for combinations. The number of ways to choose 13 cards from 52 is given by:
52 choose 13 = 52! / (13! * 39!) = 635,013,559,600
This represents the total number of ways to choose 13 cards from the deck, without regard to which player receives which cards.
To determine the number of ways to pass out 13 cards to each of the two players, we need to divide this total number by the number of ways to distribute the cards evenly between the players. Since each player receives 13 cards, we can think of the distribution as dividing the deck into two piles of 26 cards each, and then choosing 13 cards from each pile for each player. The number of ways to do this is given by:
(26 choose 13) * (26 choose 13) = (26! / (13! * 13!)) * (26! / (13! * 13!)) = 5,148,644
Therefore, there are 5,148,644 ways to pass out 13 cards to each of the two players from a deck of 52 cards containing 26 red cards and 26 black cards, assuming that the distribution is random.
to learn more about number click here:
brainly.com/question/30752681
#SPJ11
a basket of fruits contains 5 apples and 3 pears. sharon took two fruits at random. what is the probability that both fruits are apples? write your answer in the simplest form of fraction
Answers
The probability that Sharon randomly selects two apples from the basket of fruits, given that there are 5 apples and 3 pears, can be expressed as a fraction.
To find the probability, we need to consider the total number of possible outcomes and the number of favorable outcomes.
The total number of possible outcomes is the number of ways Sharon can select any two fruits from the basket, which can be calculated using combinations. In this case, there are 8 fruits in total, so the total number of possible outcomes is C(8, 2) = 28.
The number of favorable outcomes is the number of ways Sharon can select two apples from the five available in the basket, which is C(5, 2) = 10.
Therefore, the probability that both fruits Sharon selects are apples is 10/28, which can be simplified to 5/14.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
standard form of (x+4)(x-6
Answers
x^2 - 6x + 4x - 24
X^2 - 2x - 24
find a cartesian equation for the curve and identify it. r = 2 csc(θ)
Answers
The cartesian equation of the curve \(r=2 \hspace{0.1cm} csc \hspace{0.1cm} \theta\) is \(y=2\).
A Cartesian equation is essential in mathematics. It corresponds to a mathematical formula that expresses the connection between elements as a function of their positions on a plane known as Cartesian.
A two-dimensional coordinate scheme called the Cartesian plane employs a horizontal x-axis and an upward y-axis to identify locations in space.
Given that, \(r=2 \hspace{0.1cm} csc \hspace{0.1cm} \theta\).
So, \(csc\hspace{0.1cm}\theta=cosec \hspace{0.1cm}\theta\).
The equation becomes as follows:
\(r=2cosec\hspace{0.1cm} \theta\)
By using the trigonometric equation \(cosec\hspace{0.1cm} \theta=\frac{1}{sin\hspace{0.1cm}\theta}\), we get
\(r= \frac{2}{sin \hspace{0.1cm} \theta}\)
Multiplying both sides by \(sin\hspace{0.1cm}\theta\), we get
\(r \hspace{0.1cm}sin\hspace{0.1cm}\theta =2\hspace{0.1cm}\frac{sin\hspace{0.1cm}\theta}{sin\hspace{0.1cm}\theta}\)
\(rsin\hspace{0.1cm}\theta=2\)
By the parametric equations \(x=rcos\hspace{0.1cm}\theta\) and \(y=rsin\hspace{0.1cm}\theta\), we get
\(y=2\)
It is a horizantal line.
Hence, the cartesian equation of the curve \(r=2 \hspace{0.1cm} csc \hspace{0.1cm} \theta\) is \(y=2\).
Read more about cartesian equation:
https://brainly.com/question/30857232
The cartesian equation for the curve is: y = 2 This is a horizontal line passing through the point (0,2).
To find a Cartesian equation for the curve given by the polar equation r = 2 csc(θ), we will convert the polar coordinates (r, θ) into Cartesian coordinates (x, y) using the following relationships:
x = r * cos(θ)
y = r * sin(θ)
Step 1: Express r in terms of θ
r = 2 csc(θ)
Step 2: Since csc(θ) = 1 / sin(θ), rewrite the equation as
r = 2 / sin(θ)
Step 3: Express x and y in terms of r and θ
x = r * cos(θ)
y = r * sin(θ)
Step 4: Substitute r from Step 2 into the y equation
y = (2 / sin(θ)) * sin(θ)
Step 5: Simplify the equation
y = 2
The Cartesian equation for the given polar equation is y = 2, which represents a horizontal line passing through the point (0, 2).
Learn more about cartesian equation:
brainly.com/question/11676110
#SPJ11
cant solve x+4y=0
3x+2y=20
Answers
Answer:
The answer to this question is -2.
Step-by-step explanation:
First, multiply one of the equations by something that can cancel out the other variable.
3x+2y=20
3(x+4y=0)
3x+2y=20
3x+12y=0
Now, subtract both equations.
-10y=20
Now, divide both sides by -10.
y=-2
Hope this helps!
3h + 4, where h = 7 pls help
Answers
Answer:
25
Step-by-step explanation:
3 (7) + 4 =
21 + 4 = 25
good luck, hope this helps :)
Answer:
25
Step-by-step explanation:
1. we need to substitute h
so it would look like:
\(3(7)+4\\21+4\\25\)
Hope this helps and answers your question! Have a great day/night!
PLEASE HELP On a clock, what is the angle formed by the hour hand and minute hand at 1:30? Assume the hour and minute hand each move at a constant rate. A.67 B.105 C.120 D.135
Answers
Answer:
D. 135°
Step-by-step explanation:
Time is 1:30
The minute hand traveled half of full circle
The minute hand position is:
360°×1/2= 180°The hour hand traveled 1.5 hr ÷ 12 hr= 1/8 of full circle
The hour hand position is:
360°×1/8= 45°the difference between the hands:
180°-45°= 135°Choice D. 135° is the correct one
what is the perimeter of a rectangle with the points (-3,4)(2.2)(-4,1)1,-1)
Answers
The perimeter of the rectangle is approximately √29 + √37 + √29 + √41.
To find the perimeter of a rectangle, we need to calculate the lengths of all four sides and then sum them up.
Given the coordinates of the rectangle's vertices as (-3, 4), (2, 2), (-4, 1), and (1, -1), we can determine the lengths of the sides.
Side AB:
Using the distance formula, we calculate the distance between points A(-3, 4) and B(2, 2):
AB = √((2 - (-3))^2 + (2 - 4)^2) = √(5^2 + (-2)^2) = √(25 + 4) = √29
Side BC:
Using the distance formula, we calculate the distance between points B(2, 2) and C(-4, 1):
BC = √((-4 - 2)^2 + (1 - 2)^2) = √((-6)^2 + (-1)^2) = √(36 + 1) = √37
Side CD:
Using the distance formula, we calculate the distance between points C(-4, 1) and D(1, -1):
CD = √((1 - (-4))^2 + (-1 - 1)^2) = √(5^2 + (-2)^2) = √(25 + 4) = √29
Side DA:
Using the distance formula, we calculate the distance between points D(1, -1) and A(-3, 4):
DA = √((-3 - 1)^2 + (4 - (-1))^2) = √((-4)^2 + 5^2) = √(16 + 25) = √41
Now, we can sum up the lengths of all four sides to find the perimeter:
Perimeter = AB + BC + CD + DA
Perimeter = √29 + √37 + √29 + √41
So, the perimeter of the rectangle is approximately √29 + √37 + √29 + √41.
for such more question on perimeter
https://brainly.com/question/23875717
#SPJ8
Lucy Liu went shopping at Hollister with her friends together they spent a mean price of $40 on eight sweaters the first step and sweaters cost $50 $55 $30 $35 $39 $40 and $42 how much in dollars does the eighth sweater cost
Answers
Answer:he eighth sweater costs $29
Step-by-step explanation:
Let the price of the eighth sweater be re[presented as X
We know that
Mean Price =Total sum of cost of sweater bought/ Number of sweater'
Plugging in our known values we have that
40=$50+ $55+ $30+ $35+ $39+ $40 + $42+X /8
8 X 40 =291 +X
320=291 +X
X =320-291
X=29
Therefore, the eighth sweater costs $29
Answer: 29
Step-by-step explanation:
I got a question and im anwsering here bc i want the points either way how is this a high school question im in 6th this is a hw problem
if sales were low today, what is the probability that they will be average for the next three days? write your answer as an integer or decimal.
Answers
The probability of low sales for the next three days, given that sales were low today, is 1.0 or 100%.
To find the transition matrix for the Markov chain, we can represent it as follows:
| P(1 → 1) P(1 → 2) P(1 → 3) |
| P(2 → 1) P(2 → 2) P(2 → 3) |
| P(3 → 1) P(3 → 2) P(3 → 3) |
From the given information, we can determine the transition probabilities as follows:
P(1 → 1) = 1 (since if sales are low one day, they are always low the next day)
P(1 → 2) = 0 (since if sales are low one day, they can never be average the next day)
P(1 → 3) = 0 (since if sales are low one day, they can never be high the next day)
P(2 → 1) = 0.1 (10% chance of going from average to low)
P(2 → 2) = 0.4 (40% chance of staying average)
P(2 → 3) = 0.5 (50% chance of going from average to high)
P(3 → 1) = 0.7 (70% chance of going from high to low)
P(3 → 2) = 0 (since if sales are high one day, they can never be average the next day)
P(3 → 3) = 0.3 (30% chance of staying high)
The transition matrix is:
| 1.0 0.0 0.0 |
| 0.1 0.4 0.5 |
| 0.7 0.0 0.3 |
To find the probability of low sales for the next three days, we can calculate the product of the transition matrix raised to the power of 3:
| 1.0 0.0 0.0 |³
| 0.1 0.4 0.5 |
| 0.7 0.0 0.3 |
Performing the matrix multiplication, we get:
| 1.0 0.0 0.0 |
| 0.1 0.4 0.5 |
| 0.7 0.0 0.3 |
So, the probability of low sales for the next three days, given that sales were low today, is 1.0 or 100%.
To know more about probability click here :
https://brainly.com/question/32468931
#SPJ4
The complete question :
The Creamlest Cone, a local ice cream shop, classifies sales each day as "Tow." average,"or "high. "if sales are low one day, then they are always low the next day if sales are average one day, then there is a 10% chance they will be low the next day, a 4090 chance they wal be average the next day and a 50% chance they will be high the next day. If sales are high one day, then there is a 70% chance they wil be low the next day and a 30% chance they will be high the next day if state 1 = ow sales, state 2 average sales, and state 3 high sales, find the transition matnx for the Markov chain write entries as integers or decimals. If sales were low today, what is the probability that they will be low for the next three days? Write answer as an integer or decimal