Ranny is buying presents for members of his family. He wants to spend $10 less on his brother than he spends on his sister, and six dollars more than twice the amount he spends on his sister on his mother. If Ranny has $100 to spend, how much does he intend to spend on his brother? Please answer with a numerical explanation. No other explanation required.
Answers
Answer:
8
Step-by-step explanation:
Answer:
Step-by-step explanation: ahshshhshdbd
Related Questions
I want to know what is the formula for an endpoint with the midpoint of a line segement.
Answers
Answer:
Did u actually need the answer or is this another c.hat?
Step-by-step explanation:
Answer question 1-15 by 6pm

Answers
Answer:
Step-by-step explanation:
It is not really a question we can help you with you have to draw shapes for each 3 letters
4. A pizza shop has 12" pizzas with 6 slices and 16" pizzas with slices. Which pizza has bigger slices?
Answers
If ST=17 and RT=41, find RS. Use the number line below.
Answers
The length of segment RS is given as follows:
RS = 24.
What does the angle addition postulate state?The angle addition postulate states that if two or more angles share a common vertex and a common angle, forming a combination, the measure of the larger angle will be given by the sum of the measures of each of the angles.
The segment RT is the combination of segments RS and ST, hence:
RT = RS + ST.
Hence the length of segment RS is given as follows:
41 = RS + 17
RS = 24.
More can be learned about the angle addition postulate at https://brainly.com/question/24782727
#SPJ1
find an equation for the tangent plane to the surfacez 1=xy5cos(z) at the point (1,1,0)
Answers
The equation for the tangent plane to the surface at the point `(1,1,0)` is `z = 5y - 5`.
The given equation is `z=1=xy5cos(z)`.
We need to find the equation for the tangent plane to the surface at the point `(1,1,0)`.
The equation for the tangent plane can be given as: `z-z0 = f_x(x0,y0)*(x-x0) + f_y(x0,y0)*(y-y0)` where `(x0,y0,z0)` is the given point and `f_x` and `f_y` are the partial derivatives of the function `z=f(x,y)` with respect to x and y, respectively.
Let's find the partial derivatives:'f_x (x,y) = y^5 cos(z)`Differentiating `f` with respect to x, we get: `∂f/∂x = 0` since there is no x-term in the function.
Therefore, `f_x(x0,y0) = 0`.`f_y(x,y) = 5xy^4 cos(z)`Differentiating `f` with respect to y, we get: `∂f/∂y = 5x*y^4*cos(z)` Hence, `f_y(x0,y0) = 5*1*1^4*cos(0) = 5`.Therefore, the equation for the tangent plane is: `z-0 = 0*(x-1) + 5*(y-1)` Simplifying, we get: `z = 5y - 5`.
Thus, the equation for the tangent plane to the surface at the point `(1,1,0)` is `z = 5y - 5`.
#SPJ11
a company wants to study the effectiveness of a new pain relief medicine. they recruit 100100100 volunteers who suffer chronic pain. they assign each subject a number from 111 to 100100100 and use a random number generator to assign the first 505050 subjects selected to the treatment group. the remaining 505050 subjects are assigned to the control group. what type of experiment design is this?
Answers
The experimental design which is used in the study is Completely randomized design.
Completely Randomized design may be defined as a technique in which all the solutions are assigned at random so that each questions receive all the possible solutions. According to the question we know that the sample size is 100 volunteers who are suffering from chronic pain. Now, out of the 100 volunteers, 50 males and 50 females are chosen. Further out of the 50 males, 25 males are randomly assigned to the treatment group while the other 25 males are assigned to a control group. Since, the treatments are randomly assigned completely, each of the volunteers have an equal chance of receiving the treatments.
Learn more about randomized design at:
brainly.com/question/9363521
#SPJ4
if sin x = 2 9 sinx=29 , x in quadrant i, then find (without finding x). sin(2x)
cos(2x)
tan(2x)
Answers
The value of Sin(2x) ,cos(2x) and tan(2x) are sin(2x) = \(29 \sqrt{\frac{643}{4} }\), cos(2x) = -\(\frac{-99}{2}\), and tan(2x) =-\(\frac{-29}{12}\).. We can use the identity sin(2x) = 2sin(x)cos(x) to find sin(2x).
How to find the value of Sin(2x) ,cos(2x) and tan(2x) ?First, we need to find cos(x) using the Pythagorean identity.
cos(x) = √(1 - sin²(x))
cos(x) = √(1 - (29/2)²)
cos(x) = √(1 - 841/4)
cos(x) = √(643/4)
Now we can find sin(2x):
sin(2x) = 2sin(x)cos(x)
sin(2x) = 2(\(\frac{29}{2}\))(\(\frac{643}{4}\))
sin(2x) = 29\(\frac{643}{4}\)
To find cos(2x), we can use the identity cos(2x) = cos²(x) - sin²(x):
cos(2x) = cos²(x) - sin²(x)
cos(2x) = \(\frac{643}{4}\) - (\(\frac{841}{4}\))
cos(2x) = -\(\frac{198}{4}\)
cos(2x) = -\(\frac{-99}{2}\)
Finally, to find tan(2x), we can use the identity tan(2x) =\(\frac{2tan(x)}{1-tan^{2}(x) }\) :
tan(x) = sin(x)/cos(x) \(\frac{sin(x)}{cos(x)}\)
tan(x) = \(\frac{29}{2} : \frac{\sqrt{643} } }{2}\)
tan(x) = \(\frac{29}{\sqrt{643} }\)
tan²(x) = \((\frac{29}{√643})}{2}\)
tan²(x) = \(\frac{841}{643}\)
tan(2x) = \(\frac{2tan(x)}{1-tan^{2}(x) }\)
tan(2x) = (2(29/√643))/(1 - 841/643) \(\frac{\frac{2(29)}{643} }{1-\frac{841}{643} }\)
tan(2x) = -\(\frac{-29}{12}\)
Therefore, sin(2x) = \(29 \sqrt{\frac{643}{4} }\), cos(2x) = -\(\frac{-99}{2}\), and tan(2x) =-\(\frac{-29}{12}\).
Learn more about phytagoras
https://brainly.com/question/343682
#SPJ11
And this one two plz
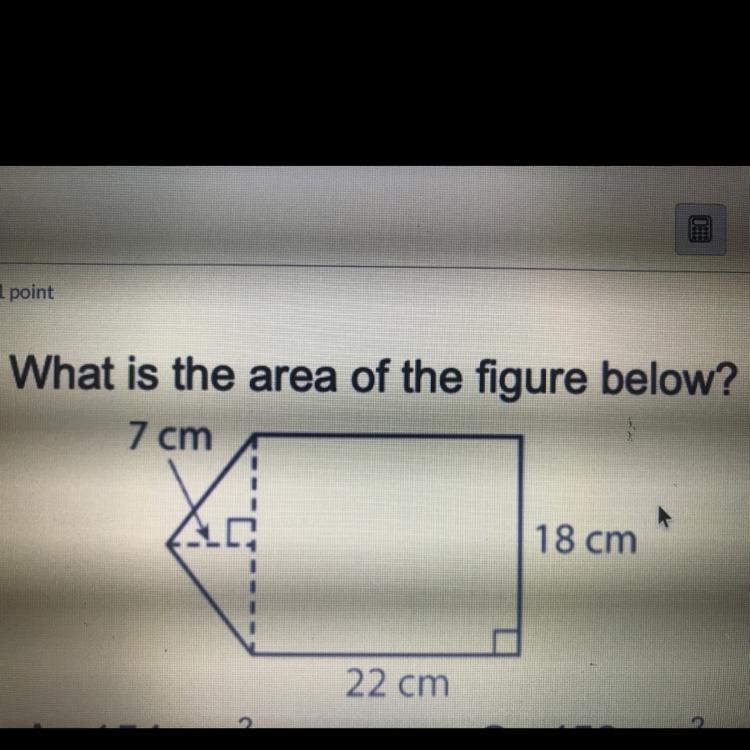
Answers
Answer:
459 cm squared
Step-by-step explanation:
The triangle has a base of 18 and a height of 7.
Do 18x7/2 to get 63 cm squared.
The rectangle has a length and width of 22 and 18.
Do 22x18 to get 396 cm squared.
Add 396 and 63 to get a total area of 459 square cm.
Answer:
Your answer is 459 cm²
Step-by-step explanation:
Find the slope of the line that passes through the points M(0,2) and N (1,7)
A. 1
B.-1
C.5
D.-5
Answers
Answer:
Hi... Your answer is... C=5
what is the length of the midsegment of this trapezoid? enter your answer in the box.
Answers
The length of the midsegment of the trapezoid is 8 units
Trapezoid
A trapezoid, also known as a trapezium, is a flat closed shape having 4 straight sides, with one pair of parallel sides. The parallel sides of a trapezium are known as the bases, and its non-parallel sides are called legs.
The midsegment of a trapezoid is the segment connecting the midpoints of the two non-parallel sides of the trapezoid and is parallel to the pair of parallel sides.
In this problem
The two non-parallel sides of the trapezoid are AD and BC
Step 1
Find the midpoint side of AD
Let
E the midpoint AD
A ( 2,4 ) D (-2,-1)
Find the x-coordinate of the midpoint AD
\(x = \frac{2-2}{2} = 0\)
Find the y-coordinate of the midpoint AD
\(y = \frac{4 - 1}{2} = 1.5\)
the point E is equal to (0, 1.5 )
Step 2
Find the midpoint side of BC
Let
F the midpoint BC
\(B ( 7,4) C ( 9, -1)\)
Find the x-coordinate of the midpoint BC
\(x = \frac{9+2}{7} = 8\)
Find the y-coordinate of the midpoint BC
\(y = \frac{4 - 1}{2} = 1.5\)
The point F is equal to ( 8 , 1.5 )
Step 3
Find the distance EF
Know that
The formula to calculate the distance between two points is equal to
\(d = \sqrt{(y2 - y1)^{2}+ (x2 -x1)^{2} }\)
we have
E ( 0 ,1.5) F ( 8, 1.5)
substitute the values
\(d = \sqrt{(1.5 - 1.5)^{2} + (8-0 )^{2} }\)
d = 8 units
Therefore
The length of the midsegment of the trapezoid is 8 units
To learn more about Trapezoid visit:
brainly.com/question/8643562
#SPJ4
I really need help with this it’s on Aleks

Answers
Answer:
y = 2
Step-by-step explanation:
Given
\(\sqrt[3]{3y+2}\) + 4 = 6 ( subtract 4 from both sides )
\(\sqrt[3]{3y+2}\) = 2 ( cube both sides )
3y + 2 = 2³ = 8 ( subtract 2 from both sides )
3y = 6 ( divide both sides by 3 )
y = 2
What are the solutions of x2 10x 16 = 0? write the equation in standard form. factor the polynomial. apply the zero product property. solve the resulting equations. x2 10x 16 = 0 (x 2)(x 8) = 0 x 2 = 0 or x 8 = 0 x = and x =
Answers
The values of x or the solution of the of provided polynomial equation are x=-2 and x=-8.
What is the factor of polynomial?The factor of a polynomial is the terms in linear form, which are, when multiplied together, give the original polynomial equation as a result.
The given polynomial equation in standard form is,
\(x^2 +10x +16 = 0\)
Now factor the polynomial.
\(x^2 +10x +16 = 0\\(x 2)(x 8) = 0\)
Apply the zero product property and find out the factors as,
\(x +2 = 0, x +8 = 0\)
Solve the resulting equations by equating both the factors one by one to the zero and find the roots.
\(x +2 = 0\\x=-2\\\)
Similarly, for x+8=0,
\(x +8 = 0\\x=-8\)
Thus, the values of x or the roots of the equation are,
\(x = -2, x =-8\)
Hence, the values of x or the solution of the of provided polynomial equation are x=-2 and x=-8.
Learn more about factor of polynomial here;
https://brainly.com/question/24380382
Answer:
-2 and -8
Step-by-step explanation:
got my answer from the person above.

Given f(x)=x*-x³-6x², for what values of x will f(x) > 0?
Answers
The values of x will f(x) > 0 for x < 0, and f(x) < 0 for -6 < x < 0 and x > -6.
To determine the values of x for which f(x) > 0, we need to find the intervals where the function is positive. Let's analyze the function f(x) = x*-x³-6x².
First, let's factor out an x from the expression to simplify it: f(x) = x(-x² - 6x).
Now, we can observe that if x = 0, the entire expression becomes 0, so f(x) = 0.
Next, we analyze the signs of the factors:
1. For x < 0, both x and (-x² - 6x) are negative, resulting in a positive product. Hence, f(x) > 0 in this range.
2. For -6 < x < 0, x is negative, but (-x² - 6x) is positive, resulting in a negative product. Therefore, f(x) < 0 in this range.
3. For x > -6, both x and (-x² - 6x) are positive, resulting in a negative product. Thus, f(x) < 0 in this range.
For such more questions on values
https://brainly.com/question/843074
#SPJ8
If a fair coin will be flipped three times, what is the probability of flipping at least two heads in a row
Answers
The probability of flipping at least two heads in a row is 3/8.
Let E be an event of flipping atleast two heads in a row.
According to the given question.
A fair coin is flipped three times.
Therefore,
The sample space when a fair coin is flipped three times is
{HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Where, H denotes of getting H and T denotes getting tail.
So, there is total eight possible outcomes we get when a fair coin is flipped.
Now, the total possible sequences or outcomes of getting or flipping atleast two heads in a row would be {HHH, HHT, THH}
⇒ Total number of favorable outcomes = 3
Therefore, the probability of flipping at least two heads in a row is given by
P(E) = number of favorable outcomes/total number of outcomes
⇒ P(E) = 3/8
Hence, the probability of flipping at least two heads in a row is 3/8.
Find out more information about probability here:
https://brainly.com/question/11234923
#SPJ4
HELP?!?
The diameter of a proton times 10 raised to what power is equivalent to the diameter of a nucleus?
Answers
Answer:
The answer is -3.
(Hope this helps)
Step-by-step explanation:
The diameter of a nucleus is much smaller than the diameter of a proton. In fact, it is about 10,000 times smaller!
If we imagine the diameter of a proton to be equal to 1 unit, then the diameter of a nucleus would be equal to 0.0001 units.
To write this in scientific notation, we can express it as 1 x 10^-3 units.
So, the diameter of a proton times 10 raised to what power is equivalent to the diameter of a nucleus?
The answer is -3.
The diameter of a proton times 10 raised to the power of -1 is equivalent to the diameter of a nucleus.
Explanation:The diameter of a proton is approximately 1.75 x 10-15 meters, and the diameter of a typical atomic nucleus is approximately 1 x 10-14 meters.
To find the power to which we need to raise 10 in order to equate the two diameters, we can set up an equation:
1.75 x 10-15 = 1 x 10-14 * 10x
Dividing both sides of the equation by 1 x 10-14, we get:
x = -1
Therefore, the diameter of a proton times 10 raised to the power of -1 is equivalent to the diameter of a nucleus.
Learn more about Proton and nucleus diameter here:https://brainly.com/question/32674365
#SPJ2
Those methods involving the collection, presentation, and characterization of a set of data in order to properly describe the various features of that set of data are called?
Answers
Those methods involving the collection, presentation, and characterization of a set of data in order to properly describe the various features of that set of data are called descriptive statistics.
Descriptive statistics:- Descriptive statistics helps to describe, summarize and organize the set of data efficiently and in an informative way, so that it'll be easier to make conclusion about the data in order to make rational decisions. This method describes the characteristics of a dataset.
Example:- The average test score for the students of a particular class, gives descriptive sense of the typical scores.
There are three types of descriptive statistics-
Univariate statistics:- It summarizes only one variable at a time.Bivariate statistics:- It compares between two variables.Multivariate statistics:- It compares between more than two variables.Thus we can conclude that, those methods involving the collection, presentation, and characterization of a set of data in order to properly describe the various features of that set of data are called descriptive statistics.
To know more about descriptive statistics refer below link:
https://brainly.com/question/13335435
#SPJ4
Part 1 of 2 Question content area top Part 1 Two of the most expensive cars in the world are car A and car B. The prices of these two cars differ by more than $. The price of car A is $. a. Assuming that you do not know which model is more expensive, write an absolute value inequality that describes this situation. Use x for the price of car B. b. What are the possibilities for the price of car B?
Answers
Considering the given situation, it is found that:
a. The absolute value inequality is: |x - 131745| > 15000.
b. The possibilities for the price of car B are of x < $116,745 or x > x > $146,745.
What is the absolute value function?The absolute value function is defined by the following piecewise rule, depending on the input of the function:
|x| = x, x ≥ 0.|x| = -x, x < 0.It gives the distance of a point x to the origin, hence, for example, |-2| = |2| = 0.
In this problem, the difference between the price of car B of x and the price of car A of $131,745 is greater than $15,000, hence the absolute value inequality that models this situation is:
|x - 131745| > 15000.
Hence the possibilities for the price of car B are:
x - 131745 < -15000 -> x < -15000 + 131745 -> x < $116,745.x - 131745 > 15000 -> x > 131745 + 15000 -> x > $146,745.What is the missing information?The complete problem is given by:
"Two of the most expensive cars in the world are car A and car B. The prices of these two cars differ by more than $15,000. The price of car A is $131,745. a. Assuming that you do not know which model is more expensive, write an absolute value inequality that describes this situation. Use x for the cost of car B. b. What are the possibilities for the price of car B?"
More can be learned about the absolute value function at https://brainly.com/question/25971887
#SPJ1
10. Given the demand = −2 − 4 + 68 and the supply function = −2 + 2 +
12. Calculate
(a) the consumer’s surplus
(b) the producer’s surplus assuming pure competition
Answers
The given demand and supply of the function has ,
Equilibrium price is Rs. 14 and the equilibrium quantity is equal to 40 units.
The consumer surplus for the given function is Rs. 1,080.
The producer's surplus for the given function is Rs. 40.
Demand of the function 'Qd' = -2P + 68
Supply of the function 'Qs' = 2P + 12
The equilibrium price and quantity by setting the demand equal to the supply.
⇒ Qd = Qs
Setting Qd equal to Qs, we get,
⇒-2P + 68 = 2P + 12
Solving for P, we get,
⇒4P = 56
⇒P = 14
Substituting P back into either the demand or supply equation, we get,
⇒Qd = -2(14) + 68
= 40
⇒Qs = 2(14) + 12
= 40
So the equilibrium price is Rs. 14 and the equilibrium quantity is 40 units.
The consumer's surplus,
= The area below the demand curve and above the equilibrium price.
⇒ Consumer's surplus
= (1/2) x (Equilibrium quantity) x (Difference between maximum price and equilibrium price)
⇒ Consumer's surplus = (1/2) x (40) x (68 - 14)
⇒ Consumer's surplus = Rs. 1,080
The consumer's surplus is Rs. 1,080.
The producer's surplus
= The area above the supply curve and below the equilibrium price.
⇒ Producer's surplus
= (1/2) x (Equilibrium quantity) x (Difference between equilibrium price and minimum price)
⇒ Producer's surplus = (1/2) x (40) x (14 - 12)
⇒ Producer's surplus = Rs. 40
The producer's surplus is Rs. 40.
Therefore, for the given demand and supply function we have,
Equilibrium price and the equilibrium quantity is equal to Rs. 14 and 40units.
Consumer’s Surplus is Rs. 1,080.
Producer's surplus is Rs. 40.
Learn more about function here
brainly.com/question/24096086
#SPJ4
The above question is incomplete , the complete question is:
Given the demand = −2P + 68 and the supply function = 2P + 12. Calculate
The equilibrium price and the equilibrium quantity
(a) the consumer’s surplus
(b) the producer’s surplus assuming pure competition
What's the y intercept

Answers
Answer:
3
Step-by-step explanation:
it intercepts the y axis at 3
Answer:
3 2
Step-by-step explanation:
I just know
Determine P(c) using the remainder theorem.. (look at image)

Answers
Answer:
P(-5) = 109
Step-by-step explanation:
Remainder theorem:If the polynomial p(x) is divided by the linear polynomial (x-a), the remainder is p(a).
Dividend = divisor * quotient + remainder.
p(x) = (x-a) * q(x) + p(a)
Here, q(x) is the quotient and p(a) is the remainder.
P(x) = 4x² - x + 4
P(-5) = 4*(-5)² - 1*(-5) + 4
= 4*25 + 5 + 4
= 100 + 5 + 4
= 109
On multiple-Choice history Test, rita received a mark of 80%. She answer 32 correctly
Answers
Let total number of questions be x.
According to the question,
80% of x is 32
or 80/100 × x = 32
or x = 32 ÷ 80/100
or x = 32 × 100/80
or x = 32 × 10/8
or x = 4 × 10
or x = 40
So, total number of questions is 40.
Write the mathematical model and use Solver to answer the following question:
A farm co-op has 6,000 acres available to plant with corn and soybeans. Each acre of corn requires 9 gallons of fertilizer/herbicide and 0.75 hour of labor to harvest. Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1hour of labor to harvest. The co-op has available at most 40,501 gallons of fertilizer/herbicide and at most 5,250 hours of labor for harvesting. Find the maximum profit if the profits per acre are $75 for corn and $40 for soybeans. Round your answer to the nearest cent if necessary.
a. $210,000.00
b. $393,750.00
c. $371,255.83
d. $180,004.44
e. $318,744.17
Answers
The maximum profit if the profits per acre are $75 for corn and $40 for soybeans is $371,255.83. Therefore, the correct option is c.
To find the maximum profit from planting corn and soybeans, we can use linear programming. Let's first define the variables and write the constraints.
Let x be the number of acres of corn and y be the number of acres of soybeans.
1. Total acre constraint: x + y ≤ 6,000
2. Fertilizer/herbicide constraint: 9x + 3y ≤ 40,501
3. Labor constraint: 0.75x + y ≤ 5,250
The objective function to maximize is the profit function: P(x,y) = 75x + 40y
Now, we will use the Solver to find the maximum profit:
Step 1: Set up a spreadsheet with the constraints and the objective function.
Step 2: Go to the Data tab and click on Solver. If Solver is not available, you may need to add it in Excel Options.
Step 3: Set the objective function by selecting the cell with the profit function.
Step 4: Choose "Max" for the objective.
Step 5: Add the constraints by selecting the corresponding cells.
Step 6: Click on "Solve" and the Solver will find the optimal values for x and y.
After using Solver, we find that the optimal values are x = 4,363.89 (corn) and y = 1,636.11 (soybeans), which yields a maximum profit of $371,255.83. Therefore, the correct answer is c: $371,255.83
Learn more about Linear programming:
https://brainly.com/question/14309521
#SPJ11
is 10\3 a improper fraction? Explain
Answers
Answer: Yes
Step-by-step explanation:
An improper fraction is any fraction that has a numerator that is greater than the denominator
please solve the problem7602 (a)Solve the differential equation by method of variation of parameters: de 26 4y +9y
Answers
The general solution of the given differential equation is \(y(x) = c1e^{3x} + c2xe^{3x} - 2/3e^{-3x}/x + 4/3e^{-3x}/x^2.\) The given differential equation is a second-order linear differential equation with constant coefficients.
To solve this equation by the method of variation of parameters, we assume that the solution can be written as
\(y = u1(x)y1(x) + u2(x)y2(x),\)
where y1(x) and y2(x) are linearly independent solutions of the homogeneous equation, which is obtained by setting the right-hand side of the given equation to zero.
The characteristic equation for the homogeneous equation is (D-3)² = 0, where D is the differentiation operator. Hence, the general solution of the homogeneous equation is \(yh(x) = c1e^{3x} + c2xe^{3x}.\)
To find the particular solution, we need to find the functions u1(x) and u2(x) by assuming that y = u1(x)y1(x) + u2(x)y2(x) satisfies the given equation. Substituting y in the differential equation, we obtain two equations involving u1'(x), u2'(x), u1(x), and u2(x). Solving these equations, we get\(u1(x) = -2/3e^{-3x}/x \; and \; u2(x) = 4/3e^{-3x}/x^2.\)
Therefore, the general solution of the given differential equation is \(y(x) = c1e^{3x} + c2xe^{3x} - 2/3e^{-3x}/x + 4/3e^{-3x}/x^2.\)
To know more about differential equations refer here:
https://brainly.com/question/14620493#
#SPJ11
Complete Question:
Solve the differential equation by method of variation of parameters: \(\frac{d^{2}y}{dx^{2}} -6 \frac{dy}{dx} + 9y = \frac{6^{3x}}{x^{2}}\)
which slope is perpendicular to the given slope: m=1/4*
Answers
Answer:
\( - \frac{4}{1} = - 4\)
Given that 1 inch = 2.54 cm, how many centimeters are there in 8 feet? Answers may be written using decimal form and should be rounded to the nearest hundredth when necessary.
Answers
Answer:
There is 243.84 cm in 8 feet.
Step-by-step explanation:
We have:
1 inch = 2.54 cm
1 feet = 12 inch
We can find the number of centimeters (n) present in 8 feet as follows:
\( n = \frac{2.54 cm}{1 inch}*\frac{12 inch}{1 ft}*8 ft = 243.84 cm \)
Therefore, there is 243.84 cm in 8 feet.
I hope it helps you!
Answer:
243.84
Step-by-step explanation:
She must determine height of the clock tower using a 1.5 m transit instrument (calculations are done 1.5 m above level ground) from a distance 100 m from the tower she found the angle of elevation to be 19 degrees. How high is the clock tower from 1 decimal place?
Answers
Step-by-step explanation:
We can use trigonometry to solve this problem. Let's draw a diagram:
```
A - observer (1.5 m above ground)
B - base of the clock tower
C - top of the clock tower
D - intersection of AB and the horizontal ground
E - point on the ground directly below C
C
|
|
|
|
| x
|
|
|
-------------
|
|
|
|
|
|
|
|
|
B
|
|
|
|
|
|
|
|
|
|
|
A
```
We want to find the height of the clock tower, which is CE. We have the angle of elevation ACD, which is 19 degrees, and the distance AB, which is 100 m. We can use tangent to find CE:
tan(ACD) = CE / AB
tan(19) = CE / 100
CE = 100 * tan(19)
CE ≈ 34.5 m (rounded to 1 decimal place)
Therefore, the height of the clock tower is approximately 34.5 m.
may you please answer this question

Answers
Answer:
Step-by-step explanation:
Vertically opposite angles are congruent.
∠A = ∠C
∠A + ∠C = 254
∠A + ∠A = 254
2∠A = 254
∠A = 254/2
∠A = 127
Linear Pair: In two adjacent angles, if the non common arms are opposite rays, then they are called linear and they add up to 180
∠A + ∠B = 180 {linear pair}
127 + ∠B = 180
∠B = 180- 127
∠B = 53°
The equation find what x is and the angle mesures

Answers
ANSWER:
\(\begin{gathered} 2x+3x-6=78 \\ x=16.8 \end{gathered}\)STEP-BY-STEP EXPLANATION:
According to the graph, the sum of these two angles is equal to 78°, therefore, the equation would be:
\(2x+3x-6=78\)If we solve the value of x it would be:
\(\begin{gathered} 5x=78+6 \\ x=\frac{84}{5} \\ x=16.8 \end{gathered}\)What do you do in your free time? :D
Answers
Answer:
sleep most definitely worth it
Answer:
heyyy
Step-by-step explanation:
I eat and watch TV. i also like drawing, and math a lot so i do those things too. I also kinda like sudoku LOL