Randy's swimming coach kept track of his average 50-meter lap times during the first 3 weeks of training. How much greater was the percent of change from Week 1 to Week 2 than from Week 2 to Week 3? Round to the nearest tenth of a percent.

Answers
The percent of the first change is greater by 2.36%.
Time in 1st week = 28.8 sec
Time in 2nd week = 27.6 sec
Time in 3rd week = 27.1 sec
∴ Change of time from week 1 to week 2 = (28.8 - 27.6) sec
= 1.2 sec
∴ Percent of change from week 1 to week 2 = \(\frac{time change}{1st week time} \times 100\) %
= \(\frac{1.2}{28.8} \times 100\) %
= 4.17%
∴ Change of time from week 2 to week 3 = (27.6 - 27.1) sec
= 0.5 sec
∴ Percent of change from week 2 to week 3 = \(\frac{Time change}{2nd week time} \times 100\) %
= \(\frac{0.5}{27.6} \times 100\) %
= 1.81%
∴ The greater change was in the first week. The amount by which it was greater is = (4.17 - 1.81) %
= 2.36%
Answer) The percent of the first change is greater by 2.36%.
To learn more about percentages:
https://brainly.com/question/26352729
#SPJ1
Related Questions
write the first six cube if natural number
Answers
Answer:
1³ = 1
2³ = 8
3³ = 27
4³ = 64
5³ = 125
6³ = 216
Step-by-step explanation:
Answer:
The cube of first six natural numbers are
1, 8, 27, 65, 125, 216
Step-by-step explanation:
Natural Numbers are known as 1, 2, 3, 4, ..., ∞
Now,
For Cube of first six natural numbers
1³ = 1
2³ = 8
3³ = 27
4³ = 64
5³ = 125
6³ = 216
Thus, The cube of first six natural numbers are
1, 8, 27, 65, 125, 216
-TheUnknownScientist
(b)
4x+3
2x-1
- 2 =
6x+2
2x-1
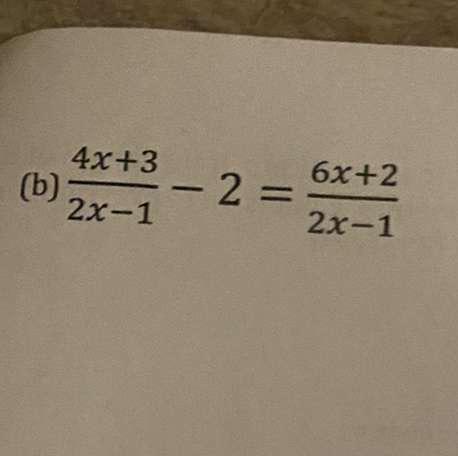
Answers
Answer:
56
Step-by-step explanation:
Is algebra.
PLEASE HELP NO LINKS OR FILES.
I don't want links.
I don't want links.
I don't want links.
I don't want links.

Answers
Answer:
(6x+1)^2
Step-by-step explanation:
Factor using the perfect square rule.
Can you round 14.392
Answers
Answer:
The answer would be 14.0
Step-by-step explanation:
you would find what the decimal is and because it is below 14.49 you would round down
Please mark as brainllest i really need it have a nice week
[o]-[o]
\___/
5y+6x=40
3y-8x=-46
x=
y=
Answers
Answer: (x,y) = (175/29, 22/29)
Step-by-step explanation:
solve the equation
y = 8 - 6/5x
3y - 8x = -46
substitute the value of y
3(8 - 6/5x) - 8x = -46
solve the equation
x = 175 / 29
substitute the value of x
y = 8 - 6/5(175/29)
solve the equation
y = 22/29
answer: (x,y) = (175/29, 22/29)
Use this new algebraic method to find equations for the line with the following properties:
A slope of −3, passing through the point (15,−50).
Show your work in the sketch box on the left.
Step 1: Substitute values for m, x, and y.
Step 2: Solve equation for b.
Step 3: Rewrite your equation with only m and b.
What is the equation of this line?
Answers
Answer:
Y = -3x + 90
Step-by-step explanation:
Y= Mx + b
M - (-3)
X - 15
Y - (-50)
Y = Mx + b
50 = (-3)(15) + b
50 = -45 + b
95 = b
Y = -3x + 90
Hope this helps
Can i please get answer ty

Answers
Juan invested $100 in a savings account the earns 5% annually. The value, A, of the investment can be calculated using the equation A=p(1+r) with and exponent of t, where p is the investment in dollars, r is the interest rate, and t is the time of years. What amount will be in the savings account in two years?
Answers
Answer:
$110.25
Step-by-step explanation:
Step one:
given
principal= $100
rate= 5%
time = 2 years
Required
The final amount
Step two:
The compound interest formula is
\(A=p(1+r)^t\)
substituting we have
\(A=100(1+0.05)^2\\\\A=100(1.05)^2\\\\A=100*1.1025\\\\A=110.25\\\\\)
The final amount is $110.25
2/3 x 12 =
3 of 20 =
10/9 x 21 =
please solve all three
Answers
Answer: 8 , 60 , 23.3
Step-by-step explanation: 2/3 x 12 = 8
3 of 20 = 60
10/9 x 21 = 70/3 = 23.3
a radiography program graduate has 4 attempts over a three-year period to pass the arrt exam. question 16 options: true false
Answers
The statement regarding a radiography program graduate having four attempts over a three-year period to pass the ARRT exam is insufficiently defined, and as a result, cannot be determined as either true or false.
The requirements and policies for the ARRT exam, including the number of attempts allowed and the time period for reattempting the exam, may vary depending on the specific rules set by the ARRT or the organization administering the exam.
Without specific information on the ARRT (American Registry of Radiologic Technologists) exam policy in this scenario, it is impossible to confirm the accuracy of the statement.
To determine the validity of the statement, one would need to refer to the official guidelines and regulations set forth by the ARRT or the radiography program in question.
These guidelines would provide clear information on the number of attempts allowed and the time frame for reattempting the exam.
Learn more about Radiography here:
brainly.com/question/31656474
#SPJ11
\(\huge\bold\red{{HELP}}\)
![[tex]\huge\bold\red{{HELP}}[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/OCEG8of0EMSXcpokJ8SLCA2Cw8KYwWz1.jpeg)
Answers
Answer: 16x\sqrt{2x}
Step-by-step explanation:
WELL HELLO BUDDY!
it is nice to see you again.
please,
whip out a piece of paper because we are going to be doing some QUICK MAFFS.
draw 512.
ok now draw two sticks coming out of 512
512
/ \
2 256
now lets keep going, do you see what im doing? i just divided 512 by 2
ok now lets go
512
/ \
2 256
/ \
16 16
im just looking for numbers that can DIVIDE 256 WITH NO DECIMALS!
ok so i keep going right? lets go.
the attached picture is the full diagram. scroll down to look at the picture.
WHAT I WANT YOU TO DO IS CIRCLE THE NUMBERS, IN PAIRS, that are at the END of the stem. so you can only circle the numbers that are at the end, the ones that dont branch off into further numbers. ok? in this way, we find that we have four pairs of 2's. and we have one 2 thats all by itself :( ok... interesting... so four pairs of 2's, lets find \(2^{4}\) (the exponent will be how many pairs you found). but we have one 2 thats all alone so lets put it in the radical... and the 16 we found as a result of
but DONT FORGET THE x's in this equation! \(x^{3}\) to be exact. we can actually put one x outside the radical since \(x^{2}\) under a radical just solves as x. the square root of \(x^{2}\) is just x, so x is outside of the radical.
but remember that we were given x^{3} to start off with! so we are gonna have one x all by his or her lonesome.
our answer will then be.... \(16x\sqrt{2x}\)
put the rest of your questions in their own posts on brainly because the other ones are too much work for just one question
![[tex]\huge\bold\red{{HELP}}[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/UaplxCGi28R6fjqWoxmst0EhR5vbUrlB.png)
Suppose a consumer's utility function is given by: \[ U=x^{1 / 5} y^{4 / 5} \] This is an example of a Cobb-Douglas model. The Cobb-Douglas model is used extensively in economics. a) Set y=1 and graph the marginal utility of x; put marginal utility on the vertical axis and x on the horizontal axis. Your graph does not have to be perfect, but it should have the correct shape. b) What is the MRS for this consumer? Explain in words what the MRS is.
Answers
a) To graph the marginal utility of x, we need to find the derivative of the utility function with respect to x. Given that y=1, the utility function becomes U=x^(1/5). Taking the derivative of U with respect to x, we get dU/dx = (1/5)x^(-4/5). This represents the marginal utility of x.
When we graph the marginal utility of x, we put the marginal utility on the vertical axis and x on the horizontal axis. Since x^(-4/5) is positive for all positive values of x, the graph of the marginal utility of x will have a positive slope that decreases as x increases. The shape of the graph will resemble a downward-sloping curve that approaches zero as x approaches infinity.
b) The MRS (Marginal Rate of Substitution) for this consumer is the rate at which the consumer is willing to trade one good for another while keeping the total utility constant. In this case, the MRS is the negative ratio of the marginal utility of x to the marginal utility of y. Mathematically, MRS = -(dU/dx)/(dU/dy).
Since y is a constant and dU/dy = 0, the MRS simplifies to MRS = -(dU/dx)/0 = undefined. This means that the consumer is not willing to trade any amount of y for x, as the marginal utility of y is zero. The consumer only derives utility from x and does not value y in terms of marginal utility.
The graph of the marginal utility of x will have a positive slope that decreases as x increases. The MRS for this consumer is undefined, indicating that the consumer does not value y in terms of marginal utility.
To know more about marginal utility , visit ;
https://brainly.com/question/34280910
#SPJ11
what is the magnitude of r prime of quantity pi over 3 end quantity given r of t equals a vector with two components, tan t and negative csc of 2t question mark one third square root of thirty four one half square root of nineteen two square root of thirteen over three four thirds square root of ten
Answers
To find the magnitude of r prime of quantity pi over 3 end quantity, we first need to take the derivative of r of t. r prime of t = a vector with two components, sec^2(t) and 2csc(2t) .Then, we can evaluate r prime of pi/3 using these components: r prime of pi/3 = a vector with two components, sec^2(pi/3) and 2csc(2(pi/3)).
Using the fact that sec^2(pi/3) = 4 and csc(2(pi/3)) = -2sqrt(3)/3, we can simplify the vector to: r prime of pi/3 = a vector with two components, 4 and -4sqrt(3)/3
Now, we can find the magnitude of this vector using the formula:
magnitude of a vector = square root of (sum of squares of its components)
magnitude of r prime of pi/3 = square root of (4^2 + (-4sqrt(3)/3)^2)
= square root of (16 + 16/3)
= square root of (64/3)
= 4/square root of 3
Multiplying this by the given constants (1/3 square root of thirty four, 1/2 square root of nineteen, 2 square root of thirteen over three, 4/3 square root of ten), we get the final answer:
magnitude of r prime of quantity pi over 3 end quantity = (4/square root of 3) * (1/3 square root of thirty four) * (1/2 square root of nineteen) * (2 square root of thirteen over three) * (4/3 square root of ten)
= 16/square root of (3 * 34 * 19 * 13 * 10/9)
= 16/square root of 2,583.49
= 16/50.83
= 0.3147 (rounded to four decimal point)
To find the magnitude of r'(π/3), we need to take the square root of the sum of the squared components:
Magnitude of r'(π/3) = √[sec^4(π/3) + (2*cot(2(π/3))*csc^2(2(π/3)))^2]
Once you evaluate the trigonometric functions at π/3 and simplify the expression, you will have the magnitude of r'(π/3).
To learn more about magnitude : brainly.com/question/25305474
#SPJ11
The area of a square whose side is 5 cm is
Answers
Answer:
25
Step-by-step explanation:
5 x 5 = 25
Answer:
the area is 20
Step-by-step explanation:
each side is 5 and a square has 4 sides
5x4=20
Recall that the constant term, C, cancels out when evaluating a definite integral and therefore, the C is traditionally omitted in the calculations. Evaluate the definite integral. integral_1/5^50/x^3 dx = [-25x^-2]+1/5^1 = F()-F (1/5) =
Answers
That the constant of integration C cancels out when we evaluate the definite integral, so we do not need to include it in the final answer.
We can evaluate the definite integral using the power rule of integration, which states that
∫ \(x^n dx = (x^(n+1))/(n+1) + C\)
where C is the constant of integration.
So, for the given definite integral, we have:
∫ \((1/(5^(50)x^3)) dx\)
\(= (-1/2) * (1/(5^(50))) * (1/x^2) + C\)
Evaluating this from x = 1 to x = 1/5, we get:
\(= (-1/2) * (1/(5^(50))) * (1/(1/5)^2) - (-1/2) * (1/(5^(50))) * (1/1^2)\)
\(= (-1/2) * (5^2) * (5^(50)) + (1/2) * (5^(50))\)
\(= - (1/2) * (5^(52)) + (1/2) * (5^(50))\)
\(= (1/2) * (5^(50)) * (1 - 5^2)\)
\(= (1/2) * (5^(50)) * (-24)\)
\(= -12 * (5^(50))\)
So, the value of the definite integral is \(-12 * (5^(50))\). Note that the constant of integration C cancels out when we evaluate the definite integral, so we do not need to include it in the final answer.
To learn more about need visit:
https://brainly.com/question/26302665
#SPJ11
Diana sold $150.00 worth of products and earns a commission of 3.5%. How much did she earn in commission?
Answers
Answer:
$5.25
Step-by-step explanation:
Take $150.00 times 3.5% to get $5.25
150(.035) = 5.25
Answer:
$5.25
Step-by-step explanation:
She earned 3.5% of $150.00.
To find a percent of a number, multiply the percent by the number.
3.5% * $150.00 =
= 0.035 * $150.00
= $5.25
Benoît has a home business selling antique watches. If he sells x watches, in thousands, his profit, P, in thousands of dollars, is given by
P=−50x^2 + 550x − 900
Determine Benoît’s break-even points
Determine his maximum profit and how many antique watches he must sell to achieve this profit.
Answers
The number of watches that just be sold is 90 and the profit is -356400.
How to calculate the profit?From the information given, the equation is given as:
P = −50x² + 550x − 900
P = -5x² + 55x - 90
= -5x² + 45x + 10x - 90
= -5x(x - 9) + 10(x - 9)
= (-5x + 10)(x - 9)
x - 9 = 0
x = 0 + 9 = 9
The watches that must be sold will be (9 × 10) = 90
The profit will be:
P = −50x² + 550x − 900
P = -50(90)² + 550(90) - 900
P = -405000 + 49500 - 900
P = -356400
Learn more about profit on:
brainly.com/question/1078746
#SPJ1
Given that ABCD is a rectangle, where EC = 7x -3 and AE=4x + 8. Find DE.
Answers
The length of segment DE on the rectangle, considering the midpoint, is given as follows:
DE = 22.67.
What is the midpoint?The midpoint of a segment divides a segment into two segments of equal length, having half the length of the entire segment.
In this problem, the diagonal of the rectangle represented by segment AC has midpoint E, hence the measure of x is calculated as follows:
EC = AE.
The measures are as follows:
EC = 7x - 3.AE = 4x + 8.Hence:
7x - 3 = 4x + 8
7x - 4x = 8 + 3
3x = 11
x = 11/3.
Segment DE is also half of a diagonal, hence it's length is obtained with the numeric value of any segment EC or AE, as follows:
DE = EC = 7x - 3 = 7 x 11/3 - 3 = 77/3 - 9/3 = 68/3 = 22.67.
Missing InformationThe rectangle is given by the image at the end of the answer.
More can be learned about rectangles at https://brainly.com/question/10489198
#SPJ1

a photograph is 5 inches by 8 inches. a frame shop charges $3.00 per inch for a silver frame. how much would it cost to buy a silver frame for the photograph?
Answers
Answer: The total cost for the frame is $78.00
Step-by-step explanation:
Photograph size = 5 inches x 8 inches
Perimeter = 5 + 5 +8 + 8
Perimeter =26 inches
Cost = $3.00 / inch for a silver frame
Total frame cost = 26 inches x $3.00 = $78.00
Please remember to vote this answer as Brainliest if I earned it!
A skydiver jumps out of a plane from a certain height. The graph below shows their
height h in feet after t seconds. What is the skydiver's initial height?

Answers
Step-by-step explanation:
At t = 0 the graph shows the initial height to be 12 544 ft
Which fraction and decimal forms match the long division problem?

Answers
Answer: C
Step-by-step explanation: C
2 divided into 9 parts is 2/9.
Let's' explain this visually
Take this pizza, (image below)
Let's say we have two pizzas for 8 friends (including ourselves), so naturally, we'll cut the pizza's each into 9 slices, 1 for each, now everyone gets 1/9 of a pizza, but there are two pizzas, so if we add 1/9+1/9, we'll get two ninths.
Now 2/9=0.2 repeating!
This is how I got my answer sorry for the vague explanation

Two very large parallel plates are perpendicular to the xx axis and have a small separation, dd. (The dimensions are distorted for purposes of visualization.) The first plate, located at x=0x=0, has a negative uniform charge density, −σ−σ, and is designated as the zero of electric potential. The second plate, located at x=dx=d, has a positive uniform charge density, +σ+σ.
20% Part (a) In terms of the variables provided in the problem statement, enter a vector expression for the electric field, E⃗ E→, that is valid in the gap between the two plates
20% Part (b) In terms of the variables provided in the problem statement, enter an expression for the electric potential that is valid in the gap between the two plates.
Answers
In the gap between the two plates, the electric field is constant and directed from the positive plate towards the negative plate. The magnitude of the electric field between the plates is given by:E = / (2).
where σ is the charge density, and ε₀ is the permittivity of free space. The direction of the electric field is from the positive plate towards the negative plate along the negative axis, denoted as E = E b where E is a unit vector in the direction.
Part (b) Expression for the electric potential in the gap between the two plates:
The electric potential between two points is defined as the work done per unit charge in moving a positive test charge from one point to another. Since the electric field in the gap between the plates is constant and only depends on the charge density, the potential difference (V) between the two plates is given by:
V = E d
where E is the magnitude of the electric field and d is the separation between the plates. The negative sign arises because the potential decreases as we move from the positive plate to the negative plate. Thus, the expression for the electric potential in the gap between the two plates is E d. The electric potential at any point within the gap is then obtained by subtracting the potential at the negative plate (which is zero) from the potential at that point.
Learn more about parallel plates here:
brainly.com/question/32237278
#SPJ11
Suppose $8,500 is compounded weekly for 34 years. If no other deposits are made, what rate is needed for the balance to quadruple in that time? Round the answer to the nearest hundredth of a percent.
Answers
To quadruple a balance in 34 years with weekly compounding and no additional deposits, an interest rate of approximately 2.74% per year is required.
To determine the required rate for the balance to quadruple in 34 years, we can use the compound interest formula:
\[A = P \left(1 + \frac{r}{n}\right)^{nt}\]
Where:
A = Final balance
P = Principal amount (initial deposit)
r = Annual interest rate (in decimal form)
n = Number of times interest is compounded per year
t = Number of years
In this case, the initial deposit is $8,500, and we want the balance to quadruple, which means the final balance (A) should be $8,500 * 4 = $34,000. The principal amount (P) and the number of years (t) are given as 8,500 and 34, respectively.
We need to solve for the interest rate (r). Since the interest is compounded weekly, n = 52 (52 weeks in a year).
The formula can be rearranged to solve for r:
\[r = n \left( \left(\frac{A}{P}\right)^{\frac{1}{nt}} - 1 \right)\]
Substituting the known values:
\[r = 52 \left( \left(\frac{34,000}{8,500}\right)^{\frac{1}{52 \times 34}} - 1 \right)\]
Calculating this expression, we find:
\[r \approx 0.0274\]
Multiplying by 100 to convert to a percentage:
\[r \approx 2.74\%\]
Therefore, the required interest rate for the balance to quadruple in 34 years, compounded weekly, is approximately 2.74%.
To learn more about interest click here brainly.com/question/30393144
#SPJ11
Simplifying the equation below! Please help.

Answers
Answer:
that would be -11
Step-by-step explanation:
it is asking for the absolute value of -7-4 however absolute value is always positive once you solve that you have a negative symbol on the outside that turns ur answer negative
Answer:
- 3
Step-by-step explanation:
- | -7+4|
Determine inside the absolute value first
-7+4 = -3
Replace inside the absolute value
- |-3|
The absolute value means take the non negative value
|-3| =3
- 3
Charles needs enough fencing to enclose a rectangular garden with a perimeter of 140 feet. If the width of its garden is to be 30 feet right the equation that can be used to solve for the length of the garden and go to mine the gardens area
Answers
The equation that can be used to find length of the garden is 140 =2l +60. The area of the rectangular garden is 1200 square feet.
To find the length of the rectangular garden, we can use the perimeter equation, which states that the perimeter of a rectangle is given by P = 2(l + w), where P is the perimeter, l is the length, and w is the width.
Given that the perimeter of the garden is 140 feet and the width is 30 feet, we can substitute these values into the equation:
140 = 2(l + 30)
Simplifying further:
140 = 2l + 60
Now, let's isolate the variable by subtracting 60 from both sides:
140 - 60 = 2l
80 = 2l
Dividing both sides by 2:
l = 40
Therefore, the length of the garden is 40 feet.
To find the garden's area, we can use the formula A = l * w, where A represents the area. Substituting the length and width values:
A = 40 * 30
A = 1200 square feet.
For more such questions on area
https://brainly.com/question/25292087
#SPJ8
A taco truck is parked at a local lunch site and customers queue up to buy tacos at a rate of one every two minutes. The arrivals of customers are completely independent of one another. It takes 50 ieconds on average to serve a customer (using a single server), with a standard deviation of 20 econds. 1. What is the average time (in seconds) it takes a customer from when they arrive to the truck until they receive their taco. seconds 2. What is the average utilization of the truck? 3. How many people, on average, are waiting in line? people 4. What is the minimum number of servers they would need to get the probability of delay to under 10% ? (Assume all servers have identical service rates.) servers
Answers
1. The average time it takes a customer from when they arrive at the truck until they receive their taco is 141.67 seconds.
2. The average utilization of the truck 141.67 seconds.
3. On average, there is 1 person waiting in line.
4. In order to achieve a delay probability of under 10%, a minimum of 1 server is required.
How to calculate the value1 The arrival rate is 1 customer every 2 minutes, which is equivalent to 0.5 customers per minute. The service rate is 1 customer per 50 seconds, which is equivalent to 1.2 customers per minute (since there are 60 seconds in a minute).
2 Average Number of Customers = (0.5 / 1.2) + 1 = 1.4167.
Average Waiting Time = 1.4167 * (50 + 50)
= 141.67 seconds.
3 The average utilization of the truck is given by the formula: Utilization = Arrival Rate / Service Rate.
Utilization = 0.5 / 1.2
= 0.4167 (or 41.67%).
The average number of people waiting in line can be calculated using the formula: Average Number of Customers - Average Utilization.
Average Number of Customers - Average Utilization = 1.4167 - 0.4167
= 1.
4 Given that the desired delay probability is 10% (or 0.1), we can rearrange the formula to solve for the utilization:
Utilization = Delay Probability / (1 + Delay Probability).
=
Utilization = 0.1 / (1 + 0.1) = 0.0909 (or 9.09%).
The utilization we calculated represents the maximum utilization to achieve a delay probability of 10%. In conclusion, to achieve a delay probability of under 10%, a minimum of 1 server is required.
Learn more about average time on
https://brainly.com/question/31955830
#SPJ1
Find the point on the line 3x + y = 8 that is closest to the point (-3,2)
Answers
Answer: To find the point on the line 3x + y = 8 that is closest to the point (-3,2), we need to minimize the distance between the line and the point.
Let (x, y) be the point on the line that is closest to (-3, 2). Then the vector from the point (-3, 2) to (x, y) is orthogonal (perpendicular) to the line. The direction vector of the line is <3, 1>, so the direction vector of the orthogonal vector is <-1/3, 1>.
Now we can write an equation for the line passing through (-3, 2) with the direction vector <-1/3, 1>:
(x - (-3))/(-1/3) = (y - 2)/1
Simplifying, we get:
3x + y = 11
This is the line passing through (-3, 2) that is orthogonal to the original line 3x + y = 8.
To find the intersection of these two lines, we can solve the system of equations:
3x + y = 8
3x + y = 11
Subtracting the first equation from the second, we get:
0 = 3
This is a contradiction, which means the two lines do not intersect. Therefore, the point on the line 3x + y = 8 that is closest to (-3, 2) does not exist.
However, we can still find the closest point to (-3, 2) on the line 3x + y = 8. This point will be the intersection of the line passing through (-3, 2) with the direction vector <-1/3, 1> and the line 3x + y = 8.
The equation of the line passing through (-3, 2) with the direction vector <-1/3, 1> is:
(x - (-3))/(-1/3) = (y - 2)/1
Simplifying, we get:
3x + y = 11
To find the intersection point with the line 3x + y = 8, we can solve the system of equations:
3x + y = 8
3x + y = 11
Subtracting the first equation from the second, we get:
0 = 3
This is a contradiction, which means the two lines do not intersect. Therefore, the point on the line 3x + y = 8 that is closest to (-3, 2) does not exist.
Step-by-step explanation:
given the derivative of the function f(x) is f′(x)=2x2−2x−60, which of the following statements is true?
a. f(x) has an inflection point at x b. f(x) has an inflection point at x = 2 c. f(x) has a local minimum at x = -5. d. f(x) has a local minimum at x = -6 e. f(x) has a local maximum at x = 6/ a
Answers
we cannot determine whether `f(x)` has a local maximum at `x = 6/a`.Thus, the correct option is C: `f(x)` has a local minimum at `x = -5`.
We know that the derivative of a function provides information about the slope of the graph of that function. Hence, we can use the information provided by the derivative of a function to make certain conclusions about the shape and behavior of the graph of that function.Now, given the derivative of the function f(x) is `f′(x) = 2x² − 2x − 60`. Let us find the second derivative of this function as follows:
`f′(x) = 2x² − 2x − 60`
Differentiating `f′(x)`, we get: `f′′(x) = 4x − 2`Now, let's discuss each option one by one:Option A: `f(x)` has an inflection point at `x`.We can conclude this by finding the point where the concavity of the function changes, i.e., the point where `f′′(x)` changes sign. For this function, `f′′(x) = 4x − 2`.We have to solve the inequality `f′′(x) < 0` for `x`. `4x − 2 < 0 ⇒ x < 1/2`Therefore, the function `f(x)` is concave down for `x < 1/2` and concave up for `x > 1/2`.Thus, the function has an inflection point at `x = 1/2`.So, this option is incorrect.Option B: `f(x)` has an inflection point at `x = 2`.We have already seen that the function has an inflection point at `x = 1/2`. So, this option is incorrect.Option C: `f(x)` has a local minimum at `x = -5`.To find the local minimum of the function, we have to find the critical points of the function. These are the points where `f′(x) = 0` or `f′(x)` is undefined. Here, `f′(x) = 2x² − 2x − 60`.We have to solve the equation `f′(x) = 0` for `x`. `2x² − 2x − 60 = 0 ⇒ x² − x − 30 = 0 ⇒ (x − 6)(x + 5) = 0`So, the critical points are `x = 6` and `x = -5`.We can find the nature of these critical points by analyzing the sign of `f′(x)` on either side of the critical points: On the interval `(-∞,-5)`, `f′(x) < 0`. On the interval `(-5,6)`, `f′(x) > 0`.On the interval `(6,∞)`, `f′(x) > 0`.So, `x = -5` is a local maximum and `x = 6` is a local minimum.Therefore, the option C is correct.Option D: `f(x)` has a local minimum at `x = -6`.This option is incorrect as the function has a local minimum at `x = 6`, not `x = -6`.Option E: `f(x)` has a local maximum at `x = 6/a`.As the value of `a` is not known, we cannot determine the value of `6/a`.
\To know more about derivative:
https://brainly.com/question/29144258
#SPJ11
The specification limits for a product are 9.87 cm and 11.61 cm. A process that produces the product has a mean of 10.85 cm and a standard deviation of 0.33 cm. What is the process capability, Cpk? a
Answers
The process capability index Cpk for the provided process ≈ 0.7687.
To calculate the process capability index Cpk, we need to use the following formula:
Cpk = min((USL - μ) / (3 * σ), (μ - LSL) / (3 * σ))
where USL is the upper specification limit, LSL is the lower specification limit, μ is the process mean, and σ is the process standard deviation.
USL = 11.61 cm (upper specification limit)
LSL = 9.87 cm (lower specification limit)
μ = 10.85 cm (process mean)
σ = 0.33 cm (process standard deviation)
Substituting these values into the formula, we can calculate Cpk:
Cpk = min((11.61 - 10.85) / (3 * 0.33), (10.85 - 9.87) / (3 * 0.33))
Cpk = min(0.76 / 0.99, 0.98 / 0.99)
Cpk = min(0.7687, 0.9899)
Cpk = 0.7687 (rounded to four decimal places)
To know more about process capability index refer here:
https://brainly.com/question/31977664#
#SPJ11
Write down the 3rd term in the sequence given by: T(n) = 2n² + n
Answers
Answer:
T(3) = 21
Step-by-step explanation:
To find the third term, substitute n = 3 into T(n) , that is
T(3) = 2(3)² + 3 = 2(9) + 3 = 18 + 3 = 21