Answers
Answer:
1. x = 102. x = -63. 944. x = 2Step-by-step explanation:
1. F and M are equal angles and sum of internal angles = 180, so
2(7x + 5) + 30 = 18014x + 10 + 30 = 18014x = 140x = 102. Triangle is equilateral as all angles are equal, so all sides are equal:
4x + 43 = -2x + 74x + 2x = 7 - 436x = -36x = -63. Isosceles triangle with equal angles of R and T:
4x + 7 = 7x - 20 (using values as per picture not text)7x - 4x = 20 + 73x = 27x = 9Angle S is
180 - 2(4*9 + 7)= 180 - 2(43) = 180 - 86 = 944. Angle 2 is supplementary with 156 as isosceles triangles and vertical angles are equal, therefore:
180 - 156 = 6 + 9x24 = 6 + 9x18 = 9xx = 2Related Questions
) Which operations are used in the expression 6(x + 8)? Choose ALL that apply.
multiplication
addition
division
subtraction
Answers
Answer:
Multiplication and addition
Step-by-step explanation:
When there are no signs between the brackets and a number, it is multiplication.
Please mark me Brainliest :)
The number of students in a literature class is 12 fewer than the number of students in sociology. The total enrollment for the two classes is 96 students. How many students are in each class?
Answers
There are 54 students in the sociology class and 42 students in the literature class.
To solve this problem, we can use algebra. Let x be the number of students in sociology, then the number of students in literature is x - 12.
Let L represent the number of students in the literature class.
Let S represent the number of students in the sociology class.
Equation 1: L = S - 12 (The number of students in the literature class is 12 fewer than the number of students in sociology.)
Equation 2: L + S = 96 (The total enrollment for the two classes is 96 students.)
To solve this system of equations, we can substitute Equation 1 into Equation 2:
(S - 12) + S = 96
S - 12 + S = 96
2S - 12 = 96
2S = 108
S = 54
Substituting the value of S back into Equation 1:
L = 54 - 12
L = 42
To know more about algebra refer here:
https://brainly.com/question/29131718#
#SPJ11
in words explain how to determine the y intercepts of a rational function. be sure to include if theres a specific way to easily find the y intercept and the possible number of y intercepts
Answers
Answer:
evaluate f(0)there will be 0 y-intercepts if f(0) is undefined, 1 otherwise.Step-by-step explanation:
You want to know how to determine the y-intercepts of a rational function, and their possible number.
Rational functionA rational function f(x) is the ratio of two polynomial functions p(x) and q(x):
f(x) = p(x)/q(x)
As such, both numerator and denominator have single function values for any value of the independent variable. The y-intercept of f(x) is ...
f(0) = p(0)/q(0)
The values of p(0) and q(0) are simply the constant terms in those respective functions.
The simple way to find the y-intercept is to look at the ratio of the constant terms in the polynomial functions making up the rational function. If that is defined, there is one y-intercept. If it is undefined (q(0)=0), then there are no y-intercepts.
<95141404393>
If a line had the equation y − 6 = -1/7(x + 2) what would the slope of a line that is
perpendicular to the equation be?
Answers
Answer:
7
Step-by-step explanation:
the equation of a line in point- slope form is
y - b = m(x - a)
where m is the slope and (a, b ) a point on the line
y = 6 = - \(\frac{1}{7}\) (x + 2) ← is in point- slope form
with slope m = - \(\frac{1}{7}\)
given a line with slope m then the slope of a line perpendicular to it is
\(m_{perpendicular}\) = - \(\frac{1}{m}\) = - \(\frac{1}{-\frac{1}{7} }\) = 7
A bridge, PR, across a river is 400 m long. Gabe is launching a canoe at point Q.
He will paddle in a diagonal line across the river to point P. He plans to return along a route beside the bridge from P to R, and then along the shore from R back to Q. How far will this be altogether?
Answers
Therefore, the total distance Gabe will paddle is 2x + 400 meters. The exact value of x depends on the width of the river, which is not provided in the given information.
To find the total distance Gabe will paddle, we need to consider the distance he will travel from Q to P, then from P to R, and finally from R back to Q.
First, let's consider the distance from Q to P. Since Gabe will paddle in a diagonal line across the river, this distance can be calculated using the Pythagorean theorem.
The length of the bridge (PR) is given as 400 meters, which is the hypotenuse of a right triangle. The width of the river can be considered as the perpendicular side, and the distance Gabe will paddle from Q to P is the other side. Let's call this distance x.
Using the Pythagorean theorem, we have:
x^2 + (width of the river)^2 = PR^2
Since the width of the river is not given, we'll represent it as w. Therefore:
x^2 + w^2 = 400^2
Next, let's consider the distance from P to R. Gabe will paddle along a route beside the bridge, which means he will travel the length of the bridge (PR) again. So, the distance from P to R is also 400 meters.
Finally, Gabe will paddle back from R to Q along the shore. Since he will follow the shoreline, the distance he will paddle is equal to the distance from Q to P, which is x.
To find the total distance, we add up the distances:
Total distance = QP + PR + RQ
= x + 400 + x
= 2x + 400
For more suchy questions on distance visit:
https://brainly.com/question/28551043
#SPJ8
When an uncertain event is expressed as a set of possible values, these values are often combined with their respective probabilities into a single mean value called what
Answers
When an uncertain event is expressed as a set of possible values, these values are often combined with their respective probabilities into a single mean value called the expected value or the mathematical expectation.
The expected value is a concept used in probability theory and statistics to represent the long-term average outcome of a random variable or uncertain event. It is calculated by multiplying each possible value of the event by its corresponding probability and summing up these products. The result is a single value that represents the average or mean outcome of the event.
The expected value provides a way to summarize the overall outcome of an uncertain event in a single numerical value. It serves as a useful tool in decision-making and risk analysis, as it helps to assess the potential outcomes and evaluate the potential gains or losses associated with different probabilities. By considering the expected value, individuals or organizations can make informed decisions based on the average outcome of the event and weigh the potential risks and rewards.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ11
Pls if anyone can solve NOW

Answers
Answer:
Step-by-step explanation:
For the graphing, we can graph both equations, and where they intercept is the answer. Okay, so we can give x random inputs and get y as an output which is one pair of coordinates. I usually like using 0 as x. y-3(0)=12. y-0=12. y=12. So for our first equation, on of the coordinates is (0,12). Now we can insert another input for x! ( I chose 1.) y-3(1)=12. y-3=12. y=15. So our other pair of coordinates for the first equation is (1,15). We can do the same with the second equation. 2y+8(0)= -4. 2y+0= -4. y=-2. The first pair of coordinates for the second equation is (0,-2). Another input we can put in is 1, again. 2y+8(1)=-4. 2y+8=-4. 2y= -12. y= -6. So our second pair of coordinates for our second equation is (1,-6). We can graph this with a graphing calculator, or mark these points and draw a straight line through them. When we draw a line through them, the part where the two lines intersect is the answer.
When we do substitution, we need to solve for x or y in the bottom equation. I want to solve for x. ( NOTE: IF YOU SOLVE FOR y, YOU STILL GET THE SAME ANSWER) x=-56-3y. Then we replace the x on the top equation with 56-3y. And we get: 2(56-3y)-y=0. We can use the distributive property. The answer I have is 112-6y-y=0. -6y-y is -7y. 112-7y=0. We can add 7y to both sides so they seperate the variables and the numbers. 112=7y. Lastly, divide by 7. For y, we get 16. To get x, we insert y, AKA 16 into x+3y= -56. x+3(16)=-56. x+48= -56. Our last step to get x is to subtract 48 from both sides leaving us with: x= -100. Our final answer is y= 16 and x= -100.
It's vacation time. You drive 90 miles along a scenic highway and then take a 5-mile run along a hiking trail. Your driving rate is nine times that of your running rate. The graph shows the total time you spend driving and running, f(x), as a function of your running rate, x.
If the total time for driving and running is 3 hours, what is your running rate?
Answers
The running rate is 5 miles per hour.Let's denote the running rate as "r" and the driving rate as "9r" (since the driving rate is nine times the running rate).
To find the running rate, we need to determine the time spent driving and running separately and then add them together to equal 3 hours.
The time spent running can be calculated as the distance divided by the running rate:
Time running = Distance / Running rate = 5 / r
The time spent driving can be calculated similarly:
Time driving = Distance / Driving rate = 90 / (9r) = 10 / r
The total time spent driving and running is given as 3 hours:
Time running + Time driving = 3
5 / r + 10 / r = 3
To solve this equation, we can combine the fractions on the left side:
(5 + 10) / r = 3
15 / r = 3
Next, we can cross-multiply to isolate the variable:
15 = 3r
Dividing both sides by 3, we find:
r = 5
Therefore, the running rate is 5 miles per hour.
learn more about fractions here: brainly.com/question/10354322
#SPJ11
f (x) = 2x² - 10x + 13
Find f (-4)

Answers
Answer:
85
Step-by-step explanation:
In this question, you would solve by plugging in -4 to x.
Solve:
f(-4) = 2(-4)² - 10(-4) + 13
= 2(16) + 40 + 13
= 32 + 40 + 13
= 72 + 13
= 85
f(-4) = 85
Please help!!!
Composition of functions~

Answers
Answer:
\(\left(g\:\circ \:\:\:h\right)\left(-4\right)=-2\)
Hence, option B) is true.
Step-by-step explanation:
Given
g(t) = t² - 2
h(t) = t + 4
To determine
\(\left(g\:\circ \:\:h\right)\left(-4\right)=?\)
Using the formula
\(\left(g\:\circ \:\:h\right)\left(-4\right)\:=g\left(h\left(-4\right)\right)\)
In order to determine g(h(-4)), first we need to determine h(-4), so
substituting t = -4 in h(t) = t + 4
h(t) = t + 4
h(-4) = -4 + 4
h(-4) = 0
so we can write
\(\left(g\:\circ \:\:\:h\right)\left(-4\right)\:=g\left(h\left(-4\right)\right)=g\left(0\right)\)
now, to determine g(0), substitute t = 0 in g(t) = t² - 2v
g(t) = t² - 2
g(0) = (0)² - 2
g(0) = 0 - 2
g(0) = -2
so, finally we get
\(\left(g\:\circ \:\:\:h\right)\left(-4\right)\:=g\left(h\left(-4\right)\right)=g\left(0\right)=-2\)
Therefore,
\(\left(g\:\circ \:\:\:h\right)\left(-4\right)=-2\)
Hence, option B) is true.
Fabio and Carlos play on a basketball team together. In the last game, Fabio had 7 points less than 2 times as many points as Carlos. Fabio scored 31 points in the game. How many points did Carlos score?
Answers
Carlos points are 12
Let , Fabio points = x= 31
Carlos points = Y
Fabio had 7 points less than 2 times as many points as Carlos.
X = 2Y - 7
X = 2Y - 7
X + 7 = 2Y
Y = (x + 7)/2
X = (31 - 7)/2
x = 24/2
X = 12
Carlos points are 12
To learn more about other example:
https://brainly.com/question/839610?referrer=searchResults
Express the product of 2x^2+6x-8 and x+3 in standard form
Answers
Answer:
2 x^ 2 + 7 x − 5
Step-by-step explanation:
2x^(2)+6x-8+x+3 and then write in standard form and came up with 2 x^ 2 + 7 x − 5.
Please try your best

Answers
Answer:
y= - 4/1x + 5
Step-by-step explanation:
Answer:
y=-4x+5
Step-by-step explanation:
4 equals the slope (rise over run) and 5 equals the y-intercept
I’ve tried solving this question but haven’t had any luck

Answers
The volume of balloon is given
\(V(r)=\frac{4}{3}(\Pi)r^2\)It is also given that the radius is increasing over time with the relation r(t)=15t.
a. The volume in terms of time is
\((V\circ r)(t)=\frac{4}{3}(\Pi)(15t)^3=4\times5\times15\times15(\Pi)t^3=4500(\Pi)t^3\)b. The volume is given 600,000 cubic inches. We have to determine the time in minutes.
\(600,000=4500\times(\Pi)\times t^3\)\(t^3=\frac{600,000}{4500\times\Pi}=42.463\)\(t=3.45\min \)Hence the time in minutes is 3.45 min.
A large university accepts 60% of the students who apply. Of the students the university accepts, 45% actually enroll. If 20,000 students apply, how many actually enroll?
Answers
Answer:
444 because 20000 divided by 45 is 444
7630 Two fair six-sided dice are tossed independently. Let X denotes the maximum of the six-sided two tosses a. What is the pmf of X? b. Find E(X). [3+2]
Answers
E(X)\(= 1(1/36) + 2(2/36) + 3(4/36) + 4(6/36) + 5(8/36) + 6(10/36)\)
= 4.47 approximately, to two decimal places. Hence, the required values are pmf of X and E(X).
Given that two fair six-sided dice are tossed independently. Let X denotes the maximum of the six-sided two tosses a. We need to find the pmf of X and E(X).a. What is the pmf of X? Probability mass function (pmf) gives the probability of each value of a random variable.
Here X represents the maximum value when two fair six-sided dice are tossed independently. The possible values of X are {1, 2, 3, 4, 5, 6}.Since X denotes the maximum value, the pmf of X isP(X = 1) = P(1, 1) = 1/36P(X = 2) = P(1, 2) + P(2, 1) = 2/36P(X = 3) = P(1, 3) + P(2, 3) + P(3, 1) + P(3, 2) = 4/36P(X = 4) = P(1, 4) + P(2, 4) + P(3, 4) + P(4, 1) + P(4, 2) + P(4, 3) = 6/36P(X = 5) = P(1, 5) + P(2, 5) + P(3, 5) + P(4, 5) + P(5, 1) + P(5, 2) + P(5, 3) + P(5, 4) = 8/36P(X = 6) = P(1, 6) + P(2, 6) + P(3, 6) + P(4, 6) + P(5, 6) + P(6, 1) + P(6, 2) + P(6, 3) + P(6, 4) + P(6, 5) = 10/36
To know more about decimal places visit:-
https://brainly.com/question/30650781
#SPJ11
what is the interest on RS. 1000 at 10 p.c.p.a for 1 year.
Answers
Answer:
Interest wil be 10% of 100 which is 10
So, interest will be Rs.10
And total amount to be payed will be 100+10 which is Rs.110
Answer:
Interest= Rs. 10
Step-by-step explanation:
Interest of Rs.100 on 10 p.c.p.a is 10% of 100
i.e., 100*10/100 = 10
Thus we have 10 as the interest
what is the percent of decrease from 10 to 4
Answers
Answer:
60% decrease i am doing decrease this year i actually just did assignment couple hours ago
Step-by-step explanation:
a researcher wishes to determine whether the salaries of professional nurses employed by private hospitals are higher than those of nurses employed by government-owned hospitals. she selects a random sample of nurses from each type of hospital and calculates the means and standard deviations of their salaries. private hospital nurses had a mean salary of $26,800 (sample of 100 nurses), while the government-owned hospital nurses had a mean salary of $25,400 (sample of 800). at the 0.01 level, can she conclude that the private hospitals pay more than the government hospitals? it is known that salaries vary normally and and it is reasonable to assume there is no difference in variability of salary between the two groups.
Answers
the researcher can conclude that private hospitals pay more than government-owned hospitals based on the sample data.
To test whether private hospitals pay more than government-owned hospitals, we can use a two-sample t-test with equal variances.
The null hypothesis is that there is no difference in mean salary between the two groups:
H0: μprivate = μgovernment
The alternative hypothesis is that private hospitals pay more than government-owned hospitals:
Ha: μprivate > μgovernment
We can use a significance level of 0.01, which corresponds to a critical value of t = 2.364 (with degrees of freedom = 898).
First, we need to calculate the pooled standard deviation:
Sp = sqrt(((n private - 1)s^2private + (n government - 1)s^2government) / (n private + n government - 2))
where n private and n government are the sample sizes, s^2private and s^2government are the sample variances, and s^2pooled is the pooled variance.
Plugging in the values, we get:
Sp = sqrt(((100-1) * 186^2 + (800-1) * 176^2) / (100 + 800 - 2)) = 176.43
Next, we calculate the test statistic:
t = (x(bar)private - x(bar)government) / (Sp * sqrt(1/n private + 1/n government))
where x(bar)private and x(bar)government are the sample means.
Plugging in the values, we get:
t = (26,800 - 25,400) / (176.43 * sqrt(1/100 + 1/800)) = 3.14
Since our test statistic (3.14) is greater than the critical value (2.364), we reject the null hypothesis and conclude that private hospitals pay more than government-owned hospitals at a significance level of 0.01.
To learn more about sample visit:
brainly.com/question/13287171
#SPJ11
the very possible foods company makes vegan versions of burgers, hot dogs, and chicken wings, and they offer two platters. platter a consists of $1$ burger, $3$ hot dogs, and $5$ chicken wings, which costs $\$16.$ platter b consists of $2$ burgers, $1$ hot dog, and $8$ chicken wings, which costs $\$20.$ a barbecue organizer requires $80$ burgers, $95$ hot dogs, and $380$ chicken wings. (there can be leftovers, but these are the minimum requirements.) what is the minimum cost (in dollars)?
Answers
The minimum cost (in dollars) for the food is found as $1,021.
Define the term minima of the function?A function's global minimum is its lowest value across the entire function's range, whereas a local minimum is its lowest value within a specific local area.Let x and y be the organizer's required purchases of Platter A and Platter B, respectively.
The stated circumstances can be summed up as follows.
x + 2y ≥ 80 . . . . . . 80 or more required hamburgers.3x + y ≥ 95 . . . . . . 95 or more required hot dogs.5x +8y ≥ 380 . . . . 380 or more required chicken wings.16x +20y = c . . . . . c must have to be minimizedThese inequality can be graphed to get the vertex of the viable region nearest to the origin.
(X, Y) Equals that vertex (20, 35).
The second vertex, which is near the origin, is (60, 10).
The order would be $1310 in price.
The price of a 20 plate A and 35 plate B order is.
20×$16 +35×$20 = $320 +700
= $1020
Thus, the minimum cost of the food is found as $1020.
To know more about the minima of the function, here
https://brainly.com/question/9180672
#SPJ4
Help me Pleaseeeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Answer:
I'm not 100%, but d is my answer because in conic sections you're on the negative side and it's the only answer with a negative integer
say that an ordered triple is pleasing if (a) , , and are in the set , and (b) both and are greater than , and at least one of them is equal to . how many pleasing triples are there?
Answers
there are 33 pleasing ordered triples.
We are given a set {1, 2, 3, 4, 5, 6}. We need to count the number of pleasing ordered triples (a, b, c), where a < b < c, and a, b, c are elements of the set.
Condition (b) requires that both b and c be greater than a. Since a can take any value from 1 to 4, the number of possibilities for (a, b, c) is:
For a = 1, there are 4 choices for b (2, 3, 4, 5) and 5 choices for c (3, 4, 5, 6, 5). However, we must exclude the case where b = c = 5, since both b and c must be greater than a. Therefore, there are 4 × 4 - 1 = 15 pleasing triples with a = 1.
For a = 2, there are 3 choices for b (3, 4, 5) and 4 choices for c (4, 5, 6, 5). However, we must exclude the case where b = c = 5, since both b and c must be greater than a. Therefore, there are 3 × 4 - 1 = 11 pleasing triples with a = 2.
For a = 3, there are 2 choices for b (4, 5) and 3 choices for c (5, 6, 5). However, we must exclude the case where b = c = 5, since both b and c must be greater than a. Therefore, there are 2 × 3 - 1 = 5 pleasing triples with a = 3.
For a = 4, there is only 1 choice for b (5) and 2 choices for c (6, 5). Therefore, there is only 1 × 2 = 2 pleasing triples with a = 4.
The total number of pleasing ordered triples is:
15 + 11 + 5 + 2 = 33
To learn more about elements visit:
brainly.com/question/13794764
#SPJ11
solve \( \frac{1}{2} (20 - 4a)6 - a\)between 4a) and 6 is suppost to be a = like 4a)=6
Answers
That is inconsistent, therefore there is no solution
When a number is increased by 35, the result
is 38. What equation fits this statement?
А
x - 35 = 38
B
x + 38 = 35
X - 38 = 35
D
x + 35 = 38
Answers
the resulting meaning equal sign
Answer:
x+35=38
Step-by-step explanation:
the equation says results which is answer so now know the 38 is on the outside
35 is positive so x+35
Which ordered pair is a solution of the equation?
-x- 4y = -10
Answers
Answer:
There are many ordered pairs that are solutions to the equation but here are the few; (0,2.5), (2,2), (4,1.5), (-2,3), (-4,3.5), (-6,4), (6,1), (8,0.5), etc...
Step-by-step explanation:
I used a graphing calculator
hope this is helpful
Please help need to get too 80%
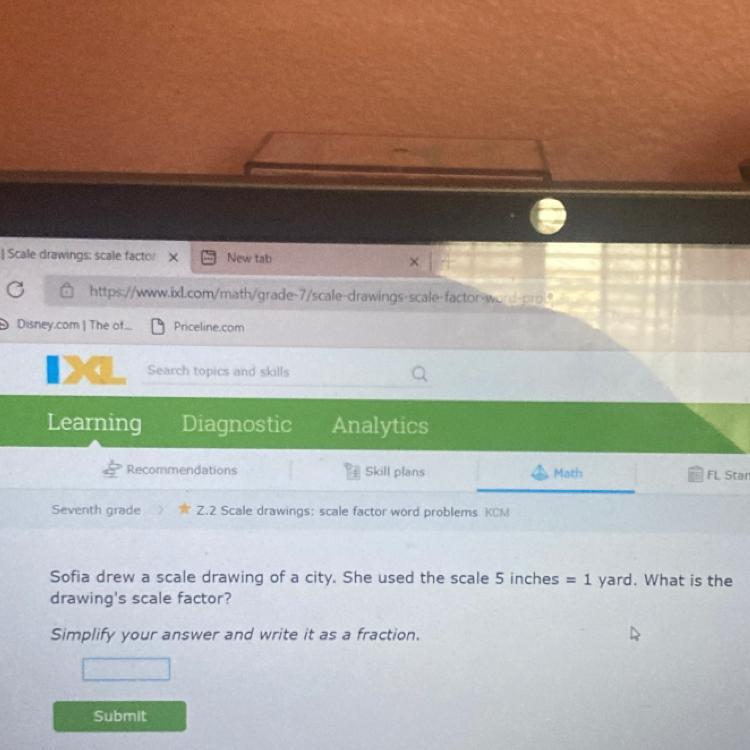
Answers
Answer:
the scale factor is 5:36.
Step-by-step explanation:
To solve the question, we note that 1 yard = 3 feet and 1 feet = 12 inches
Where the scale of the drawing is 5 inches = 1 yard,
we have the scale of the drawing is 5 inches = 36 inches
5 inches is equivalent to 36 inches in real life
That is the scale is 5 is to 36 which is 5:36.
Find the next two terms in this
sequence.
3, 12, 48, 192, [?]
Answers
Please help I need to them all

Answers
Answer:
Step-by-step explanation:
1). 6x + 7 - 18x + 4
= (6x - 18x) + (7 + 4)
= -12x + 11
2). 5x - 7x + 5x + 4 - 9
= (5x + 5x - 7x) + (4 - 9)
= 3x - 5
3). 3x + 8y - 5x + 3y
= (3x - 5x) + (8y + 3y)
= -2x + 11y
4). 17x² - 7x²- 5x + 3x + 14
= (17x² - 7x²) + (-5x + 3x) + 14
= 10x² - 2x + 14
5). 3xy - 9xy - 5x + 4x - 7 + 3
= (3xy - 9xy) + (-5x + 4x) + (-7 + 3)
= -6xy - x - 4
6). 9x + 7y - 15x + 4x - 9y
= (9x - 15x + 4x) + (7y - 9y)
= -2x - 2y
7). 3x + 7 - 5x - 8y + 4x - 2y + 7
= (3x - 5x + 4x) + (-8y - 2y) + 14
= 2x - 10y + 14
8). 3xy - xy + 15x + 4 - 11
= (3xy - xy) + 15x + (4 - 11)
= 2xy + 15x - 7
9). -8x + 3x + 7y - 5x + 4y - 2
= (-8x - 5x + 3x) + (7y + 4y) - 2
= -10x + 11y - 2
10). 3x² + 6x - 3y + 2x - 7
= 3x² + (6x + 2x) - 3y - 7
= 3x² + 8x - 3y - 7
The coordinates of point T are (0,2). The midpoint os ST is (1,-5). Find the coordinates of point S.
Answers
Answer:
...........................................
Find the inverse transformation of Laplace for:
Halla la transformada inversa de 1) \( F(s)=\frac{10}{s^{4}}+\frac{5}{s-3} \) 2) \( F(s)=\frac{8 s-9}{s^{2}+9} \) 3) \( F(s)=\frac{6}{s}+\frac{7}{s+4} \) 4) \( F(s)=\frac{2 s+3}{s^{2}-4} \)
Answers
Here is the solution to your given problem:1. Using the partial fraction method, we can write:F(s) = 10/s4 + 5/(s – 3) = (A/s) + (B/s2) + (C/s3) + (D/(s – 3))For s = 0,
the value of A can be obtained as:A = [s × F(s)]s=0 = [10/s3]s=0 = ∞For s = 3, the value of D can be obtained as:D = [s × F(s)]s=3 = [5/(s – 3)]s=3 = 5/0 = ∞
Using the same procedure as above, we can obtain the values of B and C as:B = -∞ and C = ∞Hence, the partial fraction representation of F(s) is:F(s) = (∞/s) + (-∞/s2) + (∞/s3) + (∞/(s – 3))
Taking the inverse Laplace transform, we have:f(t) = ∞ – t + ∞t2 – ∞e3t2. We can express the final solution in terms of a single equation as follows:f(t) = 2 - 2t2 + e3t/2 2. Using partial fractions, we can write:F(s) = (8s – 9)/(s2 + 9) = (As + B)/(s2 + 9) + (Cs + D)/(s2 + 9)
For s = 0,
the value of B can be obtained as:B = [s × F(s)]s=0 = [-9/(s2 + 9)]s=0 = -1For s = 0, the value of A can be obtained as:A = F(0) – B = (8 × 0 – 9)/(02 + 9) + 1 = -1/9For s = 3i,
the value of D can be obtained as:D = [s × F(s)]s=3i = [(8s – 9)/(s2 + 9)]s=3i = [(-9 + 24i)/(–18i)] = (3 – 4i)/3For s = -3i, the value of C can be obtained as:C = [s × F(s)]s=-3i = [(8s – 9)/(s2 + 9)]s=-3i = [(-9 – 24i)/(18i)] = (3 + 4i)/
, the partial fraction representation of F(s) is:F(s) = (-1/9) + (s – 1)/((s2 + 9)) + [(3 – 4i)/(3(3i + s))] + [(3 + 4i)/(3(-3i + s))]Taking the inverse Laplace transform, we have:f(t) = (-1/9) δ(t) + (1/3)cos3t + (4/9)sin3t – (1/3)e-t3sin3t3.
Using partial fractions, we can write:F(s) = 6/s + 7/(s + 4)Taking the inverse Laplace transform, we have:f(t) = 6 – 7e-4t4. Using partial fractions, we can write:F(s) = (2s + 3)/(s2 – 4) = (As + B)/(s + 2) + (Cs + D)/(s – 2)For s = 2, the value of C can be obtained as:C = [s × F(s)]s=2 = [(2s + 3)/(s2 – 4)]s=2 = 1For s = -2,
the value of A can be obtained as:A = [s × F(s)]s=-2 = [(2s + 3)/(s2 – 4)]s=-2 = 1For s = 0, the value of B can be obtained as:B = [s × F(s)]s=0 = [(2s + 3)/(s2 – 4)]s=0 = 3/(-4) = -3/4For s = 0, the value of D can be obtained as:D = F(0) – A – B = [(2s + 3)/(s2 – 4)]s=0 – 1 – (-3/4) = -1/4
Thus, the partial fraction representation of F(s) is:F(s) = [(s + 2)/4] – [(s – 2)/4]Taking the inverse Laplace transform, we have:f(t) = (1/4)(e2t – e-2t) + δ(t)
Thus, we have found the inverse transformation of Laplace for the given expressions. The solution for each question is as follows:1. \( f(t)=2-2t^{2}+\frac{1}{2}e^{\frac{3}{2}t} \)2. \( f(t)=\frac{1}{3}e^{-3t}\sin 3t+\frac{1}{3}\cos 3t+\frac{4}{9}\sin 3t-\frac{1}{9}\delta (t) \)3. \( f(t)=6-7e^{-4t} \)4. \( f(t)=\frac{1}{4}(e^{2t}-e^{-2t})+\delta (t) \).
To know more about inverse transformation, click here
https://brainly.com/question/30404106
#SPJ11
