QUESTION OF THE DAY: Judy is recreating a small version of the Statue of Liberty out of clay. The scale for the statue is 3 inches to 100 feet. If the actual height of the statue is 305 feet, what would the height of the model be in inches?
Answers
Answer:
184in
Step-by-step explanation:
Since the scale for the statue is 3 inches to 100 feet, we can say 3:100 as a ratio.
To find approximately 305 feet you must divide 305 by 100.
100 can go into 300 evenly 3 times. Since the ratio is 3:100 you should multiply how many times the 100ft fit into the 300ft and the 3in (3 x 3) which is about 9in.
One way we can do this is to divide the hight of the Statue by the model height:
305ft 20in = 15.25ft 1in or 184in (12in per foot).
And so for every inch of the model, it represents 15.25 feet.
For 305 it would be
Related Questions
The four partners in a business decide to split the profits of their company in the ratio 2 : 3 : 3 : 5 .
If the profit one year is $26, 000, then what is the largest amount of profit received by one of the four partners?
Answers
Answer:
$10,000
Step-by-step explanation:
the profit was divided to 2+3+3+5=13 parts
the largest amount of profit
=$26,000×5/13
=$10,000
Mary has a spool of ribbon to make bows. She uses 3 8 yard of the spool's ribbon to make a bow. She has 1 4 yard of the ribbon left on the spool. Which choice is the MOST reasonable tor the yards on the spool before Mary made the bows?
A) 3 8 yard
B) 1 2 yard
C) 5 8 yard
D) 5 6 yard
Answers
Answer:
5/8 yards
Step-by-step explanation:
Amount Used: 3/8 yard
Amount Remaining : 1/4
Amount started with = Amount Used + Amount Remaining
We need to find the common denominator for 8 and 4.
3/8 stays 3/8, and 1/4 becomes 2/8 (multiply the numerator and
denominator of 1/4 by 2)
3/8 + 2/8 = 5/8
-Chetan K
Answer:
b) 5/8 yard
Step-by-step explanation:
3/8 of the spool is used to make a bow.
She has 1/4 left. 1/4 = 2/8.
2/8 + 3/8 = 5/8
Point b has coordinates (-8,15) and lies on the circle whose equation is x^2+y^2=289. If an angles is drawn in standard position with its terminal ray extending through point b, what is the cosine of the angle?
Answers
Answer:
\(\cos \theta=-\dfrac{8}{17}\)
Step-by-step explanation:
Coordinates of Point b\(=(-8,15)\)
b lies on the circle whose equation is \(x^2+y^2=289\)
\(x^2+y^2=17^2\)
Comparing with the general form a circle with center at the origin: \(x^2+y^2=r^2\)
The radius of the circle =17 which is the length of the hypotenuse of the terminal ray through point b.
For an angle drawn in standard position through point b,
x=-8 which is negative
y=15 which is positive
Therefore, the angle is in Quadrant II.
\(\cos \theta=\dfrac{Adjacent}{Hypotenuse} \\$Adjacent=-8\\Hypotenuse=17\\\cos \theta=\dfrac{-8}{17} \\\cos \theta=-\dfrac{8}{17}\)
Help with geometry right triangles word problems

Answers
Referring to my photo, x is the length of the ladder.
Set up a trigonometric ratio to determine x
sin(71) = 28/x
Isolate x:
Multiply both side of the equation by x
sin(71)x = 28
Divide both sides by sin(71)
x = 28/sin(71)
Input into a calculator,
Which will get you the answer of
29.61

Anna ordered a large pizza with 2 toppings. What was the total cost of her pizza? Show your equation and the total cost.

Answers
Answer: $15.49.
Step-by-step explanation: So far, her pizza already costs $13.99 because she chose large. However, she also ordered two toppings for $0.75 each, which is $1.50. We need to add $13.99 and $1.50 to find out the total cost of her custom pizza.
$13.99 + $1.50 = $15.49.
Therefore, the total cost of her pizza is $15.49.
Have a great day! :)
I will mark you brainiest!!!
A passenger train left the station and traveled toward Las Vegas at an average speed of 55mph. A cattle train left at the same time and traveled in the opposite direction with an average speed of 65mph. Which equation best represents this situation when the trains are 960 mi apart?
A - 65x - 55(2) = 960
B - 65x - 55x = 960
C - 65x + 55(2) = 960
D - 65x + 55x = 960
E - 65(2) + 55x = 960
Answers
Answer:
The answer is b
Step-by-step explanation:
The distance traveled by the passenger train and the cattle train is equal to the total distance between them, which is 960 miles. Let x be the time (in hours) traveled by the passenger train and cattle train. Then, the equation that represents this situation is:
55x + 65x = 960
Simplifying the left-hand side of the equation, we get:
120x = 960
Dividing both sides by 120, we get:
x = 8
Therefore, the correct equation is:
B - 65x - 55x = 960
please help me. it’s a practice assignment and i don’t know what to do.

Answers
This equation cannot be solved as e to the power of any number cannot be negative. The population of a town cannot be negative. Hence, the population cannot reach 60,000.
Why do you say so ?To approximate the number of years it will take for the population to reach 40 thousand using the graph, you can look at the x-axis and visually estimate the point where the population line intersects with the 40,000 line. It looks like this will occur around year 25.
To find the number of years it will take for the population to reach 60 thousand without using the graph, you can set up the equation p(n) = 18 - e = 60,000 and solve for n.
p(n) = 18 - e = 60,000
18 - e = 60,000 + e
36 = 120,000
e = -84,000
n = log(-84,000)/log(e)
This equation cannot be solved as e to the power of any number cannot be negative. The population of a town cannot be negative. Hence, the population cannot reach 60,000.
What is data integration ?Data integration is the process of combining data from multiple sources into a single, coherent view. This can involve the merging of data from multiple databases, files, or other data storage systems into a centralized repository, or it can involve the creation of a new, unified dataset from disparate sources. The goal of data integration is to provide a single version of the truth by removing duplicates, inconsistencies, and errors, and providing a comprehensive, accurate, and up-to-date view of all relevant data. Data integration is a critical step in many data management and analytics processes and is important for ensuring the reliability and usefulness of data for decision-making.
Learn more about Data Integration here
https://brainly.com/question/27567559
#SPJ1
Lou and Jacob each sold 200 pieces of jewelry. If 20% of Lou's sales were rings, and Jacob sold 35 rings, who sold more rings? How many more?
Answers
Answer:
Step-by-step explanation:
We know Lou and Jacob each sold 200 pieces of jewelry.
Lou sold 20% of rings from the 200 pieces of jewelry.
20%* 200
= 20/100* 200
40 rings
While Jacob sold 35 rings of all the jewelry.
Therefore, Lou sold more rings. 5 more rings were sold by Lou.
This meal costs $19.00 .A sales tax is applied, followed by an automatic tip of 18 %.What is the total with tax and tip?
Answers
The total cost of he meat with tax and tip is $ 22.42
How to find the totalTo calculate the total cost with tax and tip, we need to follow these steps:
multiply the meal cost by the tip rate. when the tip rate is 18%, we have:
Tip amount = $19.00 * 0.18 = $3.42
Add the meal cost, sales tax, and tip amount to get the total cost:
Total cost = Meal cost + Sales tax + Tip amount
= $19.00 + $3.42
= $ 22.42
Therefore, the total cost with tax and tip is $22.42
Learn more about total cost at
https://brainly.com/question/5168855
#SPJ1
100 Points! PLEASE BE HONEST!!! Have some integrity :(
If f(x) = 9x+5 then what is f(4c+1) ?
Answers
\(f(4c+1)=9(4c+1)+5=36c+9+5=36c+14\)
you can choose to add the common factor which is 2(18c+7)
Show that the process X(t):=e t/2
cos(W(t)),0≤t≤T, is a martingale w.r.t. any filtration for Brownian motion and represent it as an Itô process on any time interval [0,T],T>0.
Answers
A stochastic process X(t) is called a martingale if the expected value of X(t) given all information available up to and including time s is equal to the value of X(s).
Thus, to show that the process X(t):=e^(t/2)cos(W(t)), 0 ≤ t ≤ T is a martingale w.r.t. any filtration for Brownian motion, we need to prove that E(X(t)|F_s) = X(s), where F_s is the sigma-algebra of all events up to time s.
As X(t) is of the form e^(t/2)cos(W(t)), we can use Itô's lemma to obtain the differential form:dX = e^(t/2)cos(W(t))dW - 1/2 e^(t/2)sin(W(t))dt
Taking the expectation on both sides of this equation gives:E(dX) = E(e^(t/2)cos(W(t))dW) - 1/2 E(e^(t/2)sin(W(t))dt)Now, as E(dW) = 0 and E(dW^2) = dt, the first term of the right-hand side vanishes.
For the second term, we can use the fact that sin(W(t)) is independent of F_s and therefore can be taken outside the conditional expectation:
E(dX) = - 1/2 E(e^(t/2)sin(W(t)))dt = 0Since dX is zero-mean, it follows that X(t) is a martingale w.r.t. any filtration for Brownian motion.
Now, let's represent X(t) as an Itô process on the interval [0,T]. Applying Itô's lemma to X(t) gives:
dX = e^(t/2)cos(W(t))dW - 1/2 e^(t/2)sin(W(t))dt= dM + 1/2 e^(t/2)sin(W(t))dt
where M is a martingale with M(0) = 0.
Thus, X(t) can be represented as an Itô process on [0,T] of the form:
X(t) = M(t) + ∫₀ᵗ 1/2 e^(s/2)sin(W(s))ds
Hence, we have shown that X(t) is a martingale w.r.t. any filtration for Brownian motion and represented it as an Itô process on any time interval [0,T], T > 0.
To know more about martingale visit:
brainly.com/question/32735198
#SPJ11
Select correct answer pls^^

Answers
It takes 48 hours if 12 people built the same wall.
Please see the attached picture for full solution
Hope it helps
Good luck on your assignment

Answer:
3 x 12 x 129
Step-by-step explanation:
You can get your answer
Please help, I've tried but just ended up coming up with about ten equations.

Answers
Let d be the distance from the diagonals' intersection and the larger side, so the distance from this point to the smaller side is d + 4 cm. Then d is half of the rectangle's shorter side (call it x), and d + 4 cm is half of the longer side (call it y).
The perimeter of the rectangle is 56 cm, which means
2x + 2y = 56 cm
or
x + y = 28 cm
In terms of d, this becomes
2d + 2 (d + 4 cm) = 28 cm
Solve for d :
2d + 2d + 8 cm = 28 cm
4d = 20 cm
d = 5 cm
Then the sides of the rectangle have length
x = 2d = 10 cm
y = 2 (d + 4 cm) = 2 (13 cm) = 26 cm
Can someone help me please I need to turn this in tomorrow

Answers
Answer:
1. 24 different 4-digit numbers can be formed.
Step-by-step explanation:
2. The probability that the number 3 will be the first or third digit is 1:1, which is equal to 1/2 and 50%
3. The probability is 3:1, 3/4, or 75%
4. What is the probability that the first digit will be the number 3 and the second digit will be the number 7? Answer: 1/12
The expression -210+ 12m represents a submarine that began at a depth of 210 feet below sea level and ascended at a rate of 12 feet per minute. What was the depth of the submarine after 9 minutes?
Answers
-108 is the depth of the submarine after 9 minutes.
What is Expression?An expression is combination of variables, numbers and operators.
The given expression is -210+ 12m
This expression represents a submarine that began at a depth of 210 feet below sea level and ascended at a rate of 12 feet per minute.
We need to find the depth of the submarine after 9 minutes
m=9
Now put m value in the expression
-210+12(9)
-210+108
-108
Hence, -108 is the depth of the submarine after 9 minutes.
To learn more on Expressions click:
https://brainly.com/question/14083225
#SPJ1
After a 3 hour snow storm there are 9 inches of snow on the road. What is the rate per inch?
Answers
Answer:
I inch per hour for 2 hours = 2 inches
2 inches per hour for 6 hours = 6*2 = 12 inches
1 inch per hour for 1 hour = 1 inch
2+12+1 = 15 inches of snow total
Step-by-step explanation:
credit to: musiclover10045
sin (√xy) x-y (a) Find the domain of f(x, y) = = (b) Find the limit (2 marks) sin (√xy) lim (x,y) →(0,0) x-y or show that the limit does not exist. (3 marks) (c) Find the tangent plane to the graph of f(x, y) = xy + 2x + y at (0, 0, f(0, 0)). (2 marks) (d) Check the differentiability of f(x, y) = xy + 2x + y at (0,0). (3 marks) = x² + xy in (e) Find the tangent plane to the surface S defined by the equation z² + yz R³ at the point (1, 1, 1). (5 marks) (f) Find the maximum rate of change of f(x, y) = yexy at the point (0, 2) and the direction (a unit vector) in which it occurs. (5 marks)
Answers
The maximum rate of change of f(x, y) = yexy at the point (0, 2) is 1, and the direction in which it occurs is given by the unit vector of the gradient vector, which is (6/√37, 1/√37).
(a) The domain of f(x, y) = sin(√xy) is determined by the values of x and y for which the expression inside the sine function is defined. Since the square root of a non-negative number is always defined, the domain is all real numbers for x and y where xy ≥ 0.
(b) To find the limit lim(x,y)→(0,0) sin(√xy)/(x-y), we can approach the point (0,0) along different paths and check if the limit exists and is the same regardless of the path taken.
Approach 1: x = 0, y = 0
lim(x,y)→(0,0) sin(√xy)/(x-y) = sin(0)/(0-0) = 0/0, which is an indeterminate form.
Approach 2: y = x
lim(x,y)→(0,0) sin(√xy)/(x-y) = sin(√x²)/(x-x) = sin(|x|)/0, which is undefined.
Since the limit does not exist, we can conclude that lim(x,y)→(0,0) sin(√xy)/(x-y) does not exist.
(c) To find the tangent plane to the graph of f(x, y) = xy + 2x + y at (0, 0, f(0, 0)), we need to find the partial derivatives of f(x, y) with respect to x and y, evaluate them at (0, 0), and use those values in the equation of a plane.
Partial derivative with respect to x:
∂f/∂x = y + 2
Partial derivative with respect to y:
∂f/∂y = x + 1
Evaluating at (0, 0):
∂f/∂x = 0 + 2 = 2
∂f/∂y = 0 + 1 = 1
The equation of the tangent plane is given by:
z - f(0, 0) = (∂f/∂x)(x - 0) + (∂f/∂y)(y - 0)
z - 0 = 2x + y
Simplifying, the tangent plane is:
z = 2x + y
(d) To check the differentiability of f(x, y) = xy + 2x + y at (0, 0), we need to verify that the partial derivatives ∂f/∂x and ∂f/∂y exist and are continuous at (0, 0).
Partial derivative with respect to x:
∂f/∂x = y + 2
Partial derivative with respect to y:
∂f/∂y = x + 1
Both partial derivatives are continuous at (0, 0). Therefore, f(x, y) = xy + 2x + y is differentiable at (0, 0).
(e) To find the tangent plane to the surface S defined by the equation z² + yz = x² + xy² at the point (1, 1, 1), we need to find the partial derivatives of the equation with respect to x, y, and z, evaluate them at (1, 1, 1), and use those values in the equation of a plane.
Partial derivative with respect to x:
∂(z² + yz - x² - xy²)/∂x = -2x - y²
Partial derivative with respect to y:
∂(z² + yz - x² - xy²)/∂y = z - 2xy
Partial derivative with respect to z:
∂(z² + yz - x² - xy²)/∂z = 2z + y
Evaluating at (1, 1, 1):
∂(z² + yz - x² - xy²)/∂x = -2(1) - (1)² = -3
∂(z² + yz - x² - xy²)/∂y = (1) - 2(1)(1) = -1
∂(z² + yz - x² - xy²)/∂z = 2(1) + (1) = 3
The equation of the tangent plane is given by:
z - 1 = (-3)(x - 1) + (-1)(y - 1) + 3(z - 1)
z - 1 = -3x + 3 + -y + 1 + 3z - 3
-3x - y + 3z = -2
Simplifying, the tangent plane is:
3x + y - 3z = 2
(f) To find the maximum rate of change of f(x, y) = yexy at the point (0, 2) and the direction (a unit vector) in which it occurs, we need to find the gradient vector of f(x, y), evaluate it at (0, 2), and determine its magnitude.
Gradient vector of f(x, y):
∇f(x, y) = (∂f/∂x, ∂f/∂y)
= (yexy + y²exy, exy + 2xy)
Evaluating at (0, 2):
∇f(0, 2) = (2e⁰² + 2²e⁰², e⁰² + 2(0)(2))
= (2 + 4, 1)
= (6, 1)
The magnitude of the gradient vector ∇f(0, 2) is given by:
||∇f(0, 2)|| = √(6² + 1²)
= √37
The maximum rate of change occurs in the direction of the gradient vector divided by its magnitude:
Maximum rate of change = ||∇f(0, 2)||/||∇f(0, 2)||
= √37/(√37)
= 1
To learn more about equation visit;
https://brainly.com/question/10413253
#SPJ11
Jen makes a rectangular banner. It is 3/4 yard long and 1/4 yard wide. What is the area, in square yards, of the banner? Illl give brainlist if you answer please
Answers
Answer:
3/4
Step-by-step explanation:
Determine whether the system is independent, inconsistent, or dependent.-x+4y=101/2x-2y=14Select one:O a. InconsistentO b. DependentOc. Independentd. None of these

Answers
EXPLANATION:
Given;
We are given the following system of equations;
\(\begin{gathered} -x+4y=10---(1) \\ \\ \frac{1}{2}x-2y=14---(2) \end{gathered}\)Required;
We are required to determine if the system of equations is dependent, independent or inconsistent.
Step-by-step solution;
We will start by taking equation (1). From this we make x the subject of the equation;
\(\begin{gathered} -x+4y=10 \\ \\ -x=10-4y \\ \\ Multiply\text{ }all\text{ }through\text{ }by\text{ }-1: \\ x=-10+4y \end{gathered}\)Next step is to substitute the value of x into equation (2);
\(\begin{gathered} \frac{1}{2}x-2y=14 \\ \\ \frac{1}{2}(-10+4y)-2y=14 \end{gathered}\)\(-5+2y-2y=14\)We now collect all like terms;
\(\begin{gathered} 2y-2y=14+5 \\ \\ 0=19 \end{gathered}\)This equation is not true since zero does not equal to 19.
Therefore;
ANSWER:
The equations are INCONSISTENT.
There is no solution based on our calculations above.
for a regression analysis, the value of r is 0.42. what is the value of the coefficient of nondetermination?
Answers
For a Regression Analysis that the value of R is 0.42, the value of the Coefficient of Non-Determination is 0.8236.
What is the Coefficient of Non-Determination?Coefficient of non-determination is the variation recorded in the dependent variable which is not counted by the changes in the explanatory variable. This is calculated by subtracting Coefficient of Determination from 1.
Coefficient of Non-Determination explains the amount of unexplained, or unaccounted for, variance among two variables, or among a set of variables (predictors) in an outcome variable.
The formula for the Coefficient of Non-Determination is 1 – R².
So, in this case:
1 – R²
= 1 – (0.42)²
= 1 – 0.1764
= 0.8236
Hence, the value of the Coefficient of Non-Determination is 0.8236.
Learn more about Coefficient of Non-Determination at: https://brainly.com/question/14841877
#SPJ4
help me plzzzzzzz i really need the help or else ....

Answers
The slope of the line is undefined it’s a vertical line.
Answer:
Undefined ....
hope this helps
a straight line passes through points (2,15) and (6,39) what is the y intercept?
Answers
Considering the expression of a line, the y intercept has a value of 3.
Linear equationA linear equation o line can be expressed in the form y = mx + b
where
x and y are coordinates of a point.m is the slope.b is the ordinate to the origin and represents the coordinate of the point where the line crosses the y axis.Knowing two points (x₁, y₁) and (x₂, y₂) of a line, the slope m of said line can be calculated using the following expression:
m= (y₂ - y₁)÷(x₂ - x₁)
Substituting the value of the slope m and the value of one of the points in the expression of a linear equation, the value of the ordinate to the origin b can be obtained.
y intercept in this caseBeing (x₁, y₁)=(2,15) and (x₂, y₂)=(6,39), the slope m can be calculated as:
m= (39 - 15)÷(6 - 2)
m= 24÷ 4
m= 6
Considering point 1 and the slope m, you obtain:
15= 6×2 + b
15= 12 +b
15 - 12= b
3=b
Finally, the value of the y intercept is 3.
Learn more about the equation of a line having 2 points:
brainly.com/question/12851029
brainly.com/question/19496333
#SPJ1
Given: ∆MNP, PM = 8 m∠P = 90°, m∠N = 58° Find: Perimeter of ∆MNP
(Not 22.4 or 22.43)
Please answer ASAP, brainly awarded.
Answers
Answer:
Step-by-step explanation:
Triangle MNP is a right triangle with the following values:
m∠P = 90°m∠N = 58°PM = 8Interior angles of a triangle sum to 180°. Therefore:
m∠M + m∠N + m∠P = 180°
m∠M + 58° + 90° = 180°
m∠M + 148° = 180°
m∠M = 32°
To find the measures of sides MN and NP, use the Law of Sines:
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
Substitute the values into the formula:
\(\dfrac{MN}{\sin P}=\dfrac{NP}{\sin M}=\dfrac{PM}{\sin N}\)
\(\dfrac{MN}{\sin 90^{\circ}}=\dfrac{NP}{\sin 32^{\circ}}=\dfrac{8}{\sin 58^{\circ}}\)
Therefore:
\(MN=\dfrac{8\sin 90^{\circ}}{\sin 58^{\circ}}=9.43342722...\)
\(NP=\dfrac{8\sin 32^{\circ}}{\sin 58^{\circ}}=4.99895481...\)
To find the perimeter of triangle MNP, sum the lengths of the sides.
\(\begin{aligned}\textsf{Perimeter}&=MN+NP+PM\\&=9.43342722...+4.99895481...+8\\&=22.4323820...\\&=22.43\; \sf units\; (2\;d.p.)\end{aligned}\)

Find the domain of the following graph
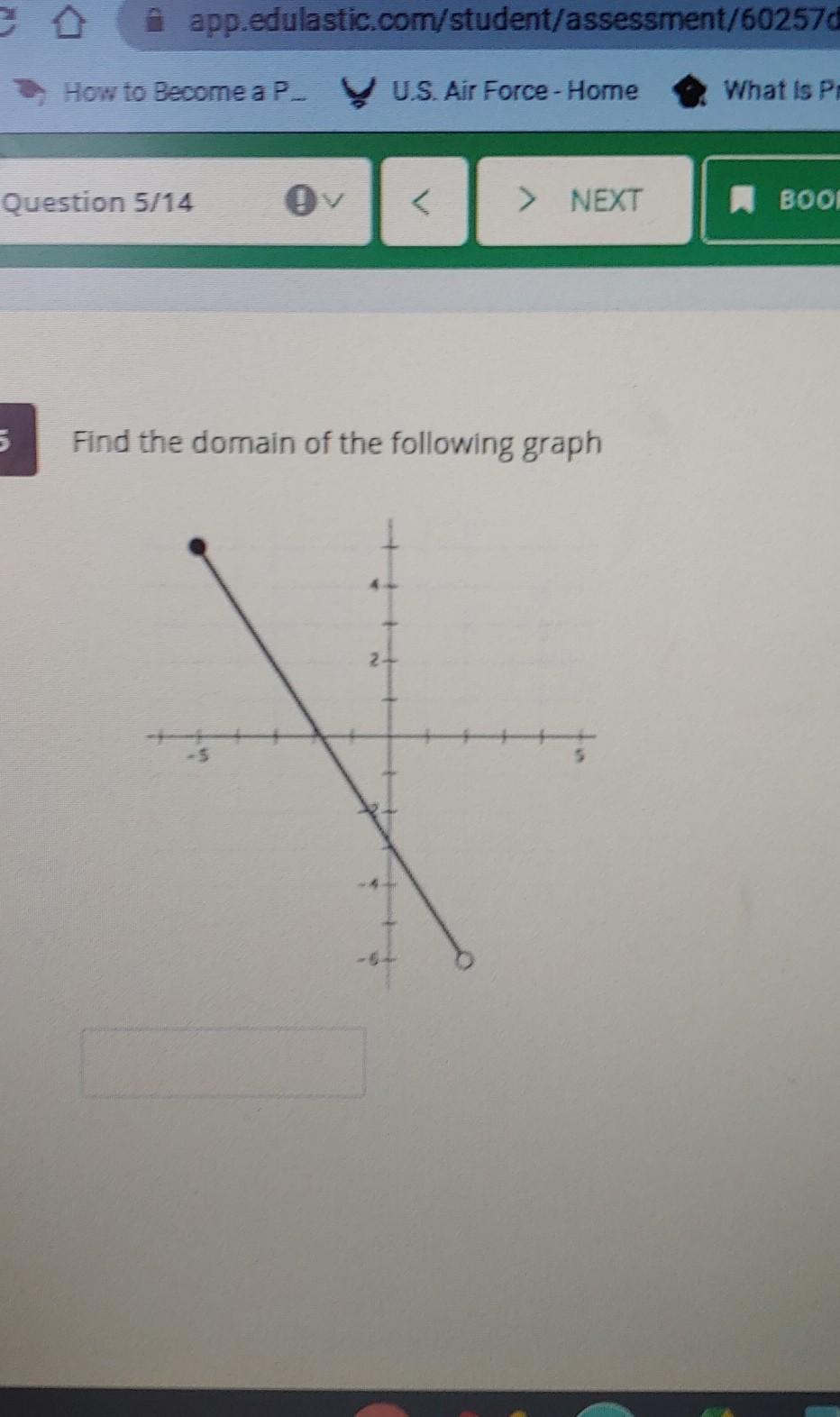
Answers
Answer:
-5,-4,-3,-2,1,0,1,2
Step-by-step explanation:
Domain are all the x values. I believe this is the answer, however the open bracket o is bit confusing, if this it not correct(still should be)try -5,and forever going. But yeah im like 99% sure im right
Let g(x) be the transformation, vertical translation 5 units down, of f(x)= 3x+9. Write the rule for g(x).

Answers
We can see the next function:
\(f(x)=3x+9\)And we need to translate this function 5 units down, which results in the function g(x).
To find the rule for g(x), we can follow the next steps:
1. We know that the general rule for a function translated k units down is given by:
\(f(x)-k\rightarrow\text{ f\lparen x\rparen has been translated by k units down \lparen where k > 0\rparen.}\)2. Then if we translate the original function by 5 units down, we will have that:
\(\begin{gathered} f(x)=3x+9 \\ \\ \\ f(x)-5=3x+9-5\rightarrow g(x) \\ \\ \end{gathered}\)3. Therefore, g(x) will be:
\(\begin{gathered} g(x)=3x+9-5=3x+4 \\ \\ g(x)=3x+4 \end{gathered}\)Hence, in summary, we have that the rule for g(x) is g(x) = 3x + 4 (option A).
consider parallelogram vwxy below use the information given in the figure to findx m

Answers
In the given parallelogram vwxy: x = 3; m∠Y = 65° and ∠YVX = 61° by (alternate interior angle).
Explain about the parallelogram?A quadrilateral with the opposing sides parallel is called a parallelogram (and thus opposite angles equal).
A parallelogram with all right angles is known as a rectangle, and a quadrilateral having equal sides is known as a rhombus. Rectangles and squares are both particular varieties of parallelograms since a square is just a degenerate instance of a rectangle.In the given parallelogram vwxy:
Parallel sides are equal.
So, 2x = 6
x = 6/2 = 3
Opposite pair of angles are also equal.
So,
∠W = ∠Y = 65°
Now,
∠YVX = 61° (alternate interior angle).
Know more about the parallelogram
https://brainly.com/question/970600
#SPJ1
The number of ounces of soda that a vending machine dispenses per cup is normally distributed with a mean of 12 ounces and a standard deviation of 4 ounces. Find the probability that more than 16 ounces is dispensed in a cup.
Answers
The probability that more than 16 ounces is dispensed in a cup is approximately 0.1587, or about 15.87%.
To solve this problem, we need to standardize the value of 16 ounces using the mean and standard deviation provided. We can do this by calculating the z-score, which is defined as:
z = (x - μ) / σ
where x is the value we want to standardize, μ is the mean, and σ is the standard deviation.
In this case, we want to find the probability that more than 16 ounces is dispensed, which can be expressed mathematically as:
P(X > 16)
where X is the random variable that represents the number of ounces of soda dispensed per cup.
To calculate this probability, we first standardize the value of 16 ounces using the mean and standard deviation provided. We have:
z = (16 - 12) / 4 = 1
Now we need to find the area under the standard normal distribution curve to the right of z = 1. We can use a standard normal distribution table or calculator to find this probability. Alternatively, we can use the complement rule, which states that:
P(X > 16) = 1 - P(X ≤ 16)
Since the normal distribution is continuous, we can use the cumulative distribution function (CDF) to find the probability of X being less than or equal to 16 ounces. Using the mean and standard deviation provided, we have:
P(X ≤ 16) = Φ((16 - 12) / 4) = Φ(1) = 0.8413
where Φ(z) is the CDF of the standard normal distribution.
Therefore, using the complement rule, we have:
P(X > 16) = 1 - 0.8413 = 0.1587
So the probability that more than 16 ounces is dispensed in a cup is approximately 0.1587, or about 15.87%.
To learn more about mathematically visit:
https://brainly.com/question/15209879
#SPJ11
pls help 50 points for reward.

Answers
Answer:
-2
Using the slope formula (y1-y2)/(x1-x2), the slope of the line is (-10-8)/(9-0), which is equal to (-18)/9= -2.
Slope
m=y2-y1/x2-x1m=8+10/0-9m=18/-9m=-2in symbolizing truth-functional claims, the word "if" used alone introduces the consequent of a condition. "only if" represents the antecedent.
Answers
In symbolizing truth-functional claims, the word "if" is used to introduce the consequent of a condition, while the phrase "only if" represents the antecedent.
Symbolizing truth-functional claims involves representing statements or propositions using logical symbols. When using the word "if" in a truth-functional claim, it typically introduces the consequent of a conditional statement. A conditional statement is a type of proposition that states that if one thing (the antecedent) is true, then another thing (the consequent) is also true. For example, the statement "If it is raining, then the ground is wet" can be symbolized as "p → q," where p represents "it is raining" and q represents "the ground is wet."
On the other hand, the phrase "only if" is used to represent the antecedent in a truth-functional claim. In a conditional statement using "only if," it states that if the consequent is true, then the antecedent must also be true. For example, the statement "The ground is wet only if it is raining" can be symbolized as "q → p," where p represents "it is raining" and q represents "the ground is wet."
In summary, when symbolizing truth-functional claims, the word "if" introduces the consequent of a condition, while the phrase "only if" represents the antecedent. These terms help express the relationships between propositions in logical statements.
Learn more about symbols here: https://brainly.com/question/30763849
#SPJ11
A semicircle with diameter 8 inches is connected to a triangle with a base length of 8 inches. The height of the triangle is 3 inches. What is the area of the composite figure? (8π + 6) in.2 (8π + 12) in.2 (8π + 18) in.2 (8π + 24) in.2
Answers
Answer:
B or (8π + 12) in.2
Step-by-step explanation:

The area of the composite figure = (8π + 12) \(inch^{2}\).
How to estimate the area of the composite figure?The composite figure is made up of a semicircle and an isosceles triangle.
The area of a semicircle = (1/2)π\(r^{2}\)
radius = 4 inch
When we substitute, the area of the semicircle is
= (1/2)π\(\times\)16
= 8π \($inch^{2}\)
Area of the isosceles triangle = (1/2)bh
= (1/2)(4+4)\(\times\)3
= 12 \(inch^{2}\)
We add the two areas to acquire the area of the composite figure to be: (8π + 12) \(inch^{2}\)
The area of the composite figure = (8π + 12) \(inch^{2}\).
Therefore, the correct answer is option b. (8π + 12) in.2
To learn more about the area of semicircle
https://brainly.com/question/12920033
#SPJ2