Question content area top Part 1 What is the longest line segment that can be drawn in a right rectangular prism that is 16 cm long, 11 cm wide, and 7 cm tall?
Please Answer ASAP!
Answers
The longest line segment in a right rectangular prism is the diagonal that connects two opposite vertices. On the first diagram attached, the green line segment connecting A and G is one such diagonals. The goal is to find the length of segment .
Look at the attached picture. The longest segment we can draw is AG (or any of its equivalent: BH, CE, DF). Let's focus on AG for example.
We can think of AG as the hypotenuse of triangle ACG. So, we need AC first. AC is itself the hypotenuse of triangle ABC,
so we have,
\(\text{AC}^2=\text{AB}^2+\text{BC}^2=11^2+7^2=170\)
Now we can resume where we stopped with triangle AGC, and we have
\(\text{AG}=\sqrt{\text{AC}^2+\text{CG}^2} =\sqrt{170+256}=\sqrt{426}\)
\(\boxed{\bold{=20.64 \ cm}}\)

Related Questions
PLEASSSSSSSSSSSSEEE HELPPP
69=-3(-3-4p)
Answers
Answer:
p = 5
Step-by-step explanation:
-3(-3-4p) = 69
-3×(-3) + -3× (-4p) = 69
9 + 12p = 69
12p + 9 - 9 = 69 - 9
12p = 60
p = 5
Hope this helps!!!
What values of x
and y
satisfy the system of equations {8x+9y=−36 x+7y=1}
Enter your answer as an ordered pair, like this: (42, 53)
If your answer includes one or more fractions, use the / symbol to separate numerators and denominators. For example, if your answer is (4253,6475),
enter it like this: (42/53, 64/75)
If there is no solution, enter "no"; if there are infinitely many solutions, enter "inf."
Answers
The solution to the system of equations is (x, y) = (-261/47, 44/47) as an ordered pair.
To solve the given system of equations:
Equation 1: 8x + 9y = -36
Equation 2: x + 7y = 1
We can use the method of substitution or elimination to find the values of x and y. Let's use the method of substitution:
From Equation 2, we can solve for x:
x = 1 - 7y
Substituting this value of x into Equation 1:
8(1 - 7y) + 9y = -36
8 - 56y + 9y = -36
-47y = -44
y = 44/47
Substituting the value of y back into Equation 2 to find x:
x + 7(44/47) = 1
x + 308/47 = 1
x = 1 - 308/47
x = (47 - 308)/47
x = -261/47
Therefore, as an ordered pair, the solution to the system of equations is (x, y) = (-261/47, 44/47).
Learn more about system of equation on:
https://brainly.com/question/12526075
This is the answer for your question

Answers
Answer:
this is the right answer ..ok
Can someone help me please I will mark u brilliant

Answers
Answer:
I think the answer is option 3
Step-by-step explanation:
Answer: The box plot that represents this data is option 3.
Step-by-step explanation:
help pls anyone? pls

Answers
Can you help me in this question?

Answers
Answer: I think its B
Step-by-step explanation: My friend answered it.
The diameter of a circle is 34 yards. What is the circle's area? Use 3.14 for .
Answers
Answer:
907.46 mm2
Step-by-step explanation:
Area of circle = (¶d^2)/4
d = 34 mm
Therefore
Area A = (3.14 x 34^2)/4
= 907.46 mm2
\(907.43 \: {yrds}^{2} \)
Step-by-step explanation:
The formula to find the area of a circle is:
\(\pi {r}^{2} \)
since pi is 3.14 then, and the radius is half of the diameter, then:
\(diameter = 34 \\ radius = \frac{34}{2} \\ radius = 17\)
Therefore;
\(area = \pi {r}^{2} \\ area = (3.14) {(17)}^{2} \\ = 3.14 \times 289 \\ = 907.46 {yrds}^{2} \)
can you help me solve this

Answers

what is the answer to this equation 21 x ___=7
Answers
Answer:
the answer is 3
Step-by-step explanation:
21 x 3 =7
hope it helps
Answer:
21/7
Step-by-step explanation:
Move 7 to next side with opposite process it is multiple after move it will be divided so 21x (21/7) it will be 7 although (21/7)equivalent to 1/3
"The intersection of two planes is a line" is a statement that is generally accepted as true, but
cannot be proven to be true. What type of statement is this?
1. defined
2. undefined
3. postulate
4. proof
Answers
A postulate is something that is assumed to be true and there isn't a proof for it as its something foundational to help set up further proofs later down the road. Another example of a postulate is that a line is defined by two distinct points.
What is the value of the expression −51 − 17 − (−37)?
Answers
Answer:
-31
Step-by-step explanation:
2 negatives make a positive so you have -51-17+37 which equals -31
write the volume formula beside the solid figure

Answers
Answer:
cube(v=l×l×l)
cylinder (v= πr^2h)
cone(v=1/3πr^2h)
rectangular prism (v= area of base×lenght)
pyramid (v=1/3×area of base×h)
Step-by-step explanation:
Cube:-a^3
Cuboid:-lbh
Cylinder :-pi r^2h
Cone:-1/3pi r^2h
15. Tim can finish painting his barn in 10 hours. It takes
his wife JoAnn only 8 hours to do the same job. If they
work together, how long will it take them to complete the
job?
Answers
Answer:
4 4/9
is the time it will take
Which graph represents the function g(z)=√2-1+1?
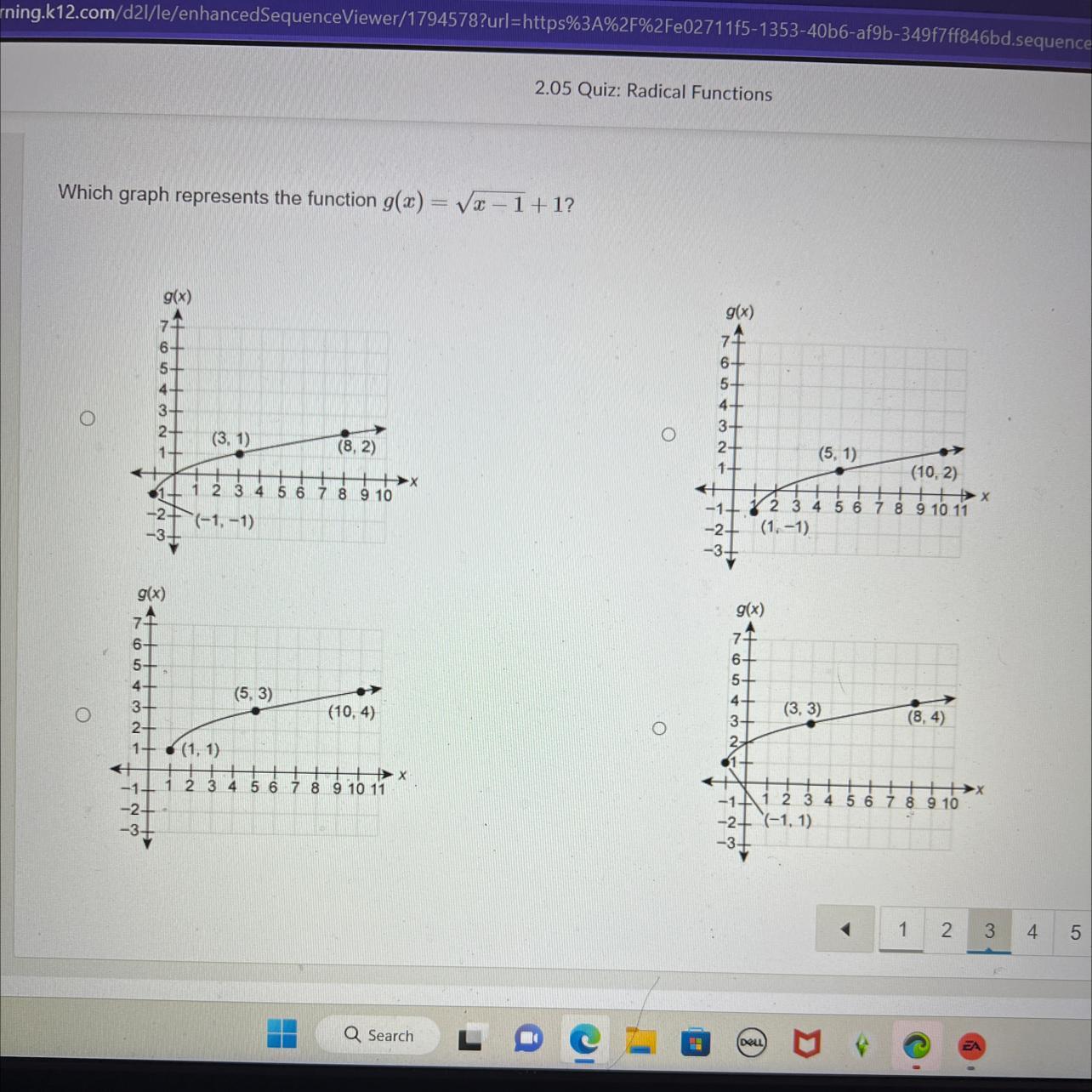
Answers
In response to the given question, we can state that Because it is independent of z, the function g(z) is a constant function. In particular, g(z) equals 2 - 1 + 1 = 2.
what is function?Mathematicians examine numbers and complex variations, equations and associated structures, forms and their locations, and prospective positions for these things. The term "functioning" signifies the connection between a collection of inputs, each of which has a corresponding output. A function is a connection of inputs and results in which each input leads to a single, identifiable outcome. Each function is assigned a domain, a codomain, or a scope. The letter f is widely used this to denote functions (x). The symbol for admission is an x. The four primary types of usable functions are on operations, one-to-one capabilities, so multiple functionality, in capabilities, and then on functions.
Because it is independent of z, the function g(z) is a constant function. In particular, g(z) equals 2 - 1 + 1 = 2.
To know more about function visit:
https://brainly.com/question/28193995
#SPJ1
Brandon is building a desk that is 42 inches long. A piece of wood that he bought is 4 feet long. How much does Brandon have to cut off that piece of wood to make it the same length as his desk?
A. 2 inches B. 6 inches C. 12 inches D. 2 feet
Answers
Answer:
6 inches
Step-by-step explanation:
there are 12 inches in a foot
4 ft * 12 = 48 inches
48 - 42 = 6
Cut off 6 inches
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
2 (x + 6) + 7 please help me with this
Answers
Answer:
2x+19
Step-by-step explanation:
Write the equation of the line graphed below

Answers
Consider the complex number on the complex plane and the complex number z2 = 6 – 3i.
On a coordinate plane, the y-axis is labeled imaginary and the x-axis is labeled real. Point Z 1 is (2, 1).
When z1 and z2 are added together, the result moves z1 6 units ____
and 3 units
.
The real part of z1 + z2 is ____
.
The imaginary part of z1 + z2 is ____
i.

Answers
When z1 and z2 are added together, the result moves z1 6 units right
and 3 units down.
The real part of z1 + z2 is 8.
The imaginary part of z1 + z2 is –2i.
When z1 and z2 are added together, the result moves z1 6 units right and 3 units down.
The real part of z1 + z2 is 8.
The imaginary part of z1 + z2 is -2.
What are complex numbers?A complex number is of the form a + bi, a, b are Real numbers, and i = √(-1). It is used to determine the values of square roots of negative numbers. It is represented in the coordinate plane with the real part on the x-axis and imaginary part b on the y-axis, the ordered pair being (a, b).
How do we solve the given question?In the question, we are given two complex numbers,
z1 = 2 + i
z2 = 6 - 3i
These points are represented on the Coordinate plane as a circle and a triangle respectively. We calculate their sum, z3.
To add Complex Numbers, the real parts are added to the real parts and the imaginary to the imaginary.
∴ z3 = z1 + z2 = (2 + i) + (6 - 3i) = (2+6) + (1-3)i = 8 -2i.
This point is represented as a square on the Coordinate plane.
By observing the coordinate plane, we can say that:
When z1 and z2 are added together, the result moves z1 6 units right and 3 units down.
Observing z3, we can tell that its real part is 8, and its imaginary part is -2.
∴ The real part of z1 + z2 is 8
∴ The imaginary part of z1 + z2 is -2
Learn more about Complex Numbers at
https://brainly.com/question/10662770
#SPJ2

Inequalities - Introduction
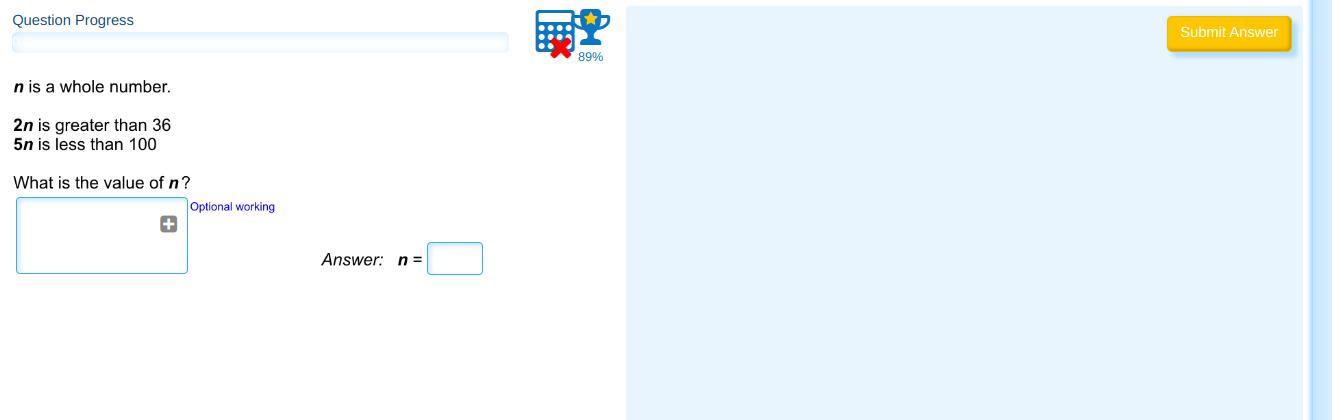
Answers
Answer:
n = 19
Step-by-step explanation:
2n > 36 ( divide both sides by 2 )
n > 18
and
5n < 100 ( divide both sides by 5 )
n < 20
so n > 18 and n < 20
thus n = 19
One weekend Bill earned 3 times as much as Jim. Tom earned $5 more than Jim.
Answers
Earning of Jim, Bill and Tom are $x, $3x, and $(x + 5) respectively.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
Let Jim earned $x in one weekend.
Bill earned 3 times as much as Jim which is $3x.
Tom earned $5 more than Jim which is $(x + 5).
Sum of their all earnings will be,
= $(x + 3x + x + 5).
= $(5x + 5).
So, Jim is the least earner and Bill is the most earner.
The main concept of these types of questions is to form the expression interpreting from the given statements.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ1
16 Triangle ABC is translated to triangle A'B'C' by
the following motion rule.
(x, y)(x+2y-5)
-8 -6
G
A. (4,-4)
B. (2,-5)
C. (0.6)
D. (-2.5)
N
8
6
B
-2
S
-6
-8
2
What will be the coordinates of A'?
6 8

Answers
Answer:
To find the coordinates of A' after the translation, we need to apply the motion rule to the coordinates of A:
(x, y) → (x + 2y - 5, y - 6)
Substituting the coordinates of point A, which is (4, -4), into this motion rule, we get:
A' = (4 + 2(-4) - 5, -4 - 6) = (-3, -10)
Therefore, the coordinates of A' after the translation are (-3, -10).
Answer this for me please

Answers
The function values are f(10) = 198 and g(-6) = 24/7; the range of h(x) is 3/5 < h(x) < 31/25 and the inverse function is p-1(x) = -(1 + 3x)/(5 + x)
Calculating the function valuesGiven that
f(x) = 2x^2 - 2
g(x) = 4x/(x - 1)
So, we have
f(10) = 2(10)^2 - 2 = 198
g(-6) = 4(-6)/(-6 - 1) = 24/7
The range of h(x)Here, we have
h(x) = (7x - 4)/5x
Where
1 < x < 5
So, we have
h(1) = (7(1) - 4)/5(1) = 3/5
h(5) = (7(5) - 4)/5(5) = 31/25
So the range is 3/5 < h(x) < 31/25
The inverse of p(x)Here, we have
P(x) = (5x - 1)/(3 - x)
So, we have
x = (5y - 1)/(3 - y)
This gives
3x - xy = 5y - 1
So, we have
y(5 + x) = -1 - 3x
This gives
y = -(1 + 3x)/(5 + x)
So, the inverse function is p-1(x) = -(1 + 3x)/(5 + x)
Read more about functions at
https://brainly.com/question/28532394
#SPJ1
you are given the following probability distribution for a stock probability outcome 5 6 5 18 1 a compute the expected return 0.5 0.06 0.5 0.18 6 2 b compute the standard deviation 3 c compute the coefficient of variation
Answers
If probability distribution for a stock probability outcome is 5, 6 ,5 ,18, 1.
a) The expected return is 1.56
b) The standard deviation is 5.1715
c) The coefficient of variation is 331.25%.
To calculate the expected return, we multiply each possible outcome by its probability and then sum the results. For example, the expected return from a 5% return is calculated as 0.5 x 5%, or 0.025. We do this for each possible outcome and then sum the results to get the expected return for the investment.
In this case, the expected return is 1.56, which means that over the long run, we can expect to earn an average return of 1.56% on this investment.
The standard deviation is a measure of how much the possible outcomes of an investment vary from the expected return. A higher standard deviation means that the possible returns are more spread out, while a lower standard deviation means that the possible returns are more tightly clustered around the expected return.
To calculate the standard deviation, we first need to calculate the variance, which is the average of the squared deviations from the expected return.
To calculate the variance, we first calculate the deviation of each possible outcome from the expected return. For example, the deviation of a 5% return from the expected return of 1.56% is 5% - 1.56% = 3.44%.
We then square each deviation and multiply it by the probability of that outcome. We do this for each possible outcome, and then sum the results to get the variance. In this case, the variance is 26.7424, which means that the possible returns are quite spread out.
The coefficient of variation is a measure of the risk per unit of return. It is calculated by dividing the standard deviation by the expected return and then multiplying by 100% to get a percentage. In this case, the coefficient of variation is 331.25%, which means that the investment is quite risky relative to its expected return.
To learn more about probability click on,
https://brainly.com/question/13054919
#SPJ4
The box plots summarize the data for heights of players on a national
basketball team and a national volleyball team.
Basketball
Volleyball
72 73 74 75 76
77
78
79
Which conclusion can you draw from the displays
one!
O
On average, there is a wide spread of heights of
O
basketball players are shorter than these volleyball pla
O
basketball players have the same height as these
On average
players.
On averag
tball players are taller than these volleyb
Answers
(Diagram of the box plots is attached below)
Options:
A. 75% of the volleyball players’ heights are equal to or greater than the median basketball players’ heights
B. 75% of the volleyball players’ heights are equal to or greater than the median basketball players’ heights
C. 25% of the basketball players’ heights are equal to or greater than the median volleyball players’ heights
D. 75% of the basketball players’ heights are equal to or greater than the median volleyball players’ heights
Answer:
D. 75% of the basketball players’ heights are equal to or greater than the median volleyball players’ heights
Step-by-step Explanation:
Based on the box plots given in the diagram attached below, the median height of volleyball players is 79.
Also, from the data set of basketball players, we can approximately infer that the heights from Q2, Q3, and Q4 make up 75% of the data set of the heights of basketball players.
Heights at Q2 in the data set of basketball players starts from 79, which is equal to the median height of volleyball players.
Therefore, from the displays, we can conclude that "75% of the basketball players’ heights are equal to or greater than the median volleyball players’ heights".

Algebra Question
68% Oppose year round school
32% Favor year round school
Error +/- 5%
The error given in the graph represents the actual percent could be 5% more or 5% less than the percent reported by the survey.
A. Write and solve an absolute value equation to determine the least and greatest percent of students who could be in favor of year-round school.
B. A classmate claims that ⅓ of the student body is actually in favor of year-round school. Does this conflict with the survey data? Explain.
*can't add graph for some reason
Answers
A. To determine the least and greatest percentage of students who could be in favor of year-round school, we can use the error given in the survey, which is +/5%. Let's denote the actual percentage of students in favor of year-round school as x.
The least percentage can be found by subtracting 5% from the reported percentage of 32%:
32% - 5% = 27%
So, the least percentage of students in favor of year-round school is 27%.
The greatest percentage can be found by adding 5% to the reported percentage of 32%:
32% + 5% = 37%
Therefore, the greatest percentage of students in favor of year-round school is 37%.
Hence, the least percentage is 27% and the greatest percentage is 37%.
B. A classmate claiming that ⅓ of the student body is actually in favor of year-round school conflicts with the survey data. According to the survey, the reported percentage in favor of year-round school is 32%, which is not equal to 33.3% (⅓). Therefore, the classmate's claim contradicts the survey results.
It's important to note that the survey provides specific data regarding the percentages of students in favor and opposed to year-round school. The claim of ⅓ being in favor does not align with the survey's findings and should be evaluated separately from the survey data.
i mark as brainliest

Answers
Answer:
the answer is 5129 so c I'm pretty sure
The ratio of dogs to cats at the Humane Shelter is 3:9. If there are 45 dogs at the Humane Shelter, how many cats are there?
A. 405
B. 120
C. 135
D. 110
Answers
Answer:
c) 135
Step-by-step explanation:
dog ratio is 3
45 ÷ 3 = 15
therefore ratio 1 is 15
ratio 9
9×15 = 135
Find the value of Y.

Answers
The value of the side y is 3√3. Option C
How to determine the value of the sideIt is crucial to note the different types of trigonometric identities.
They are;
sinetangentcotangentsecantcosecantcosineFrom the diagram shown, we have that;
The angle θ = 60 degrees
The opposite side = y
The adjacent side = 3
Let's use the tangent identity
tan 60 = y/3
Find the value
√3 = y/3
cross multiply
y = 3√3
Hence, the value is 3√3
Learn about trigonometric identity on:
https://brainly.com/question/7331447
#SPJ1
PLS HELP GIVING 50 POINTS

Answers
(2)/19
When we divide the fraction 2/19, the quotient is .105 . . . We will only include three digits past the decimal point since we must round to the nearest tenth. Because 0 is in the hundredths place, which is less than 4, we must remove all the digits after .1.
Therefore, your answer is: .1