Question 9 OT 10
The lines shown below are perpendicular. If the green line has a slope of -2/3
. what is the slope of the red line?

Answers
Answer:
(3/2)
Step-by-step explanation:
A perpendicular line has a slope that has the negative inverse of the reference line. The green line's slope of -(2/3) becomes (3/2) for a perpendicular line. The red line has two points we can use to calculate slope, just to check.
(-3,-5) and (5,7)
Rise = (7 - (-5)) = 12
Run = (5-(-3)) = 8
Slope = (12/8) or (3/2)
Related Questions
5 + m > -2 OR 2m < -20

Answers
Answer:
m > -7 OR m < -10
Step-by-step explanation:
5 + m > -2
5 + m + 2 > 0
5 + 2 > - m
7 > -m
-7 > m
2m < -20
m < -20 / 2
m < -10
Please help me!!
There were 36 campers at Yosemite Creek. They
had 10 large pepperoni pizzas to share equally.
How much pizza can each camper have?
Answers
Aim receive 18 dollar from hi father in a week. The ratio of the amount of money he pend to the amount of money
Answers
As per the given Ratio difference between the amount of money spent and the amount of money saved in a week is $2.
In mathematics, what is a ratio?A ratio is an ordered pair of numbers a and b, denoted by the symbol a / b, where b does not equal zero. A proportion is an equation that sets two ratios equal to each other.
What exactly is the ratio formula?The ratio formula can be used to represent a ratio as a fraction. For any two quantities, say a and b, the ratio formula is a:b = a/b. Because a and b are separate amounts for two portions, the total quantity is given as (a + b).
et 5x be the money he spends and 4x be the amount he saves
therefore, 5x+4x= 18
9x= 18
x= 18/9= 2
Tom spends, 5×2 = $10
and he saves, 4×2= $8
Difference, = $10-$8= $2
Therefore, as per the given ratio in the question difference between the amount of money spent and the amount of money saved in a week is $2.
To know more about ratios visit:
https://brainly.com/question/13419413
#SPJ4
Tom receives $18 from his father in a week. The ratio of the amount of
the money he spends to the amount of money he saves in a week is 5:4
What is the difference between the amount of money spent and
amount of money saved in a week?
what is the missing measurement (w) for the poster of spongebob.

Answers
To make a poster you have to keep the ratio between lenght and height (otherwise it will look weird)
This is:
\(\frac{12\operatorname{cm}}{20\operatorname{cm}}=\frac{w}{36\operatorname{cm}}\)the prescriber orders medication f 150 mcg po q.12h. the pharmacy sends a bottle labeled: medication f 0.05 mg/ml. how many milliliters will the nurse administer with each dose?
Answers
The nurse will have to administer 3 milliliters with each dose.
When the prescriber orders medication f 150 mcg po q.12h, the pharmacy sends a bottle labeled:
medication f 0.05 mg/ml.
Milliliters will the nurse administer with each dose :
The conversion factor from mcg to mg is 1/1000.
Therefore, 150 mcg = 150/1000 = 0.15 mg.
The nurse has to administer 0.15 mg of medication f per dose.
The medication f available with the pharmacy is 0.05 mg/ml.
So, the nurse has to administer 0.15 mg in a single dose, which is equal to three times the quantity of medication f available in the bottle (0.05 mg/ml).
Therefore, the nurse has to administer 3 ml (0.05 mg/ml × 3 ml) of medication f with each dose.
For similar question on conversion into milliliters
https://brainly.com/question/30400914
#SPJ11
Write as an algebraic expression: the difference of 27 and 5
Answers
The algebraic expression of the statement given as the difference of 27 and 5 is 27 - 5
How to write the statement as an algebraic expression?The statement is given as:
the difference of 27 and 5
Difference means minus.
The minus sign is represented as -
This means that the statement given as: the difference of 27 and 5
Can be represented as
27 minus 5
So, have
27 - 5
Hence, the algebraic expression of the statement given as the difference of 27 and 5 is 27 - 5
Read more about algebraic expression at
https://brainly.com/question/4344214
#SPJ1
What is the y-coordinate of the point that divides the directed line segment from J to K into a ratio of 2:3? m
Answers
The y-coordinate of the point that divides the directed line segment from J to K into a ratio of is 5.
The coordinates of point that divides the line segment into m:n ratio can be obtained as follows,
Coordinates of point = \((\frac{mx_{2}+ nx_{1} }{m+n} \frac{my_{2}+ ny_{1}}{m+n} )\)
The coordinate of point J is (-3,1)
The coordinate of point K is (-8,11)
Consider the point that divides the line segment into 2:3 ratio as P(x,y).
The coordinates of point that divides the line segment into 2:3 ratio can be calculated as follows,
\(Coordinates of P = (\frac{3(-3)+2(-8)}{2+3}, \frac{3(1)+2(11)}{2+3} )\)
\(= (\frac{-9-16}{5}, \frac{3+22}{5} )\\\\= (\frac{-25}{5} \frac{25}{5} )\)
= (-5,5)
Hence the answer is The y-coordinate of the point that divides the directed line segment from J to K into a ratio of 2:3 is 5.
To learn more about coordinates click here https://brainly.com/question/17206319
#SPJ9
Se tienen tres tanques de la misma altura (5 metro) pero sus formas son diferentes. El primero es de base circular de 3 metros de radio, el segundo su base es elíptica y su eje mayor y menor mide 6 y 4 metros respectivamente. El último tanque es un cono invertido, con una base circular de 3 metros de radio. Si en todos se llena agua con un caudal de 1.5 litros por cada segundo, determine la razón de cambio de la altura respecto al tiempo.
Answers
Answer:
1.-dh/dt = 5.31*10⁻⁵ m/seg
2.-dh/dt = 1.99*10⁻⁵ m/seg
3.-dh/dt = 1.59*10⁻⁴ m/seg
Step-by-step explanation:PREGUNTA INCOMPLETA NO SE INDICAN LAS FORMAS DE LOS TANQUES.
Asumiremos que los tres tanques son:
el primero cilindro recto de Vc = π*r²*h ( r es radio de la base y h la altura)
el segundo asumiremos que es eliptico recto de Ve = π*a*b*h aqui a y b son los ejes de la elipse y h la altura
El tercero es un cono invertido Vco = 1/3 *π*r²*h ( r es el radio de la base.
1.-Caso del cilindro
Vc = π*r²*h
Derivando en ambos miembros de la expresión tenemos:
dV(c) / dt = π*r²*dh/dt
Sustituyendo
1.5 Lts/seg = 3.14 * (3)²*dh/dt
1.5/1000 m³/seg = 28.26 m² dh/dt
1.5/ 28260 m = dh/dt
Despejando dh/dt
dh/dt = 1.5 / 28260 = 5.31*10⁻⁵ m/seg
dh/dt = 5.31*10⁻⁵ m/seg
2.-La elipse
Ve = π*a*b*h
Aplicando el mismo procedimiento tenemos:
DVe/dt = 1.5 Lts/seg = π* 6*4* dh/dt
1.5 /1000 = 75.36 *dh/dt
dh/dt = 1.5 / 75360 m/seg
dh/dt = 1.99*10⁻⁵ m/seg
3. El cono invertido
Vco = (1/3)*π*r²*h
DVco/dt = (1/3)*π*r²*dh/dt
1.5/1000 = 9.42 *dh/dt
dh/dt = 1.5/9420
dh/dt = 1.59*10⁻⁴ m/seg
The basketball team lost their last 6 games. They lost by a total of 48 points. Find their average number of points relative to their opponents
Answers
Answer:
8
Step-by-step explanation:
8 njdjijfvffjbjghbggfbgkljhbhgf9igripogr9fkhj siad said had to n be 20 things long sorry
find the marked angle of

Answers
Answer:
∠ C = 100°
Step-by-step explanation:
since 2 sides of the triangle are congruent then the triangle is isosceles with base angles congruent.
consider the angle inside the triangle to the left of 140°
this angle and 140° are a linear pair and sum to 180°
angle + 140° = 180° ( subtract 140° from both sides )
angle = 40°
then the angle on the left of the triangle = 40° ( base angles congruent )
the sum of the angles in a triangle = 180° , so
∠ C + 40° + 40° = 180°
∠ C + 80° = 180° ( subtract 80° from both sides )
∠ C = 100°
a shape is shown on the graph
Which of the following is a reflection of the shape

Answers
Answer:
one reflection would be (-2, -2) (-2,-4) and (-6, -2)
Step-by-step explanation:
Hope this helps
statistics using r
Suppose we roll a die 60 times. What is the probability of rolling 15 or fewer sixes? First, estimate this by hand using a normal approximation. Then compare to the true probability found with R.
Answers
The probability of the binomial distribution:
R
Copy code
sum(dbinom(0:15, size = 60, prob = 1/6))
To estimate the probability of rolling 15 or fewer sixes when rolling a die 60 times, we can use a normal approximation.
In this case, we can assume that rolling a six follows a binomial distribution with parameters n = 60 (number of trials) and p = 1/6 (probability of success, which is rolling a six).
To estimate the probability using a normal approximation, we need to calculate the mean (μ) and standard deviation (σ) of the binomial distribution and then use these values to approximate the probability using a normal distribution.
The mean of a binomial distribution is given by μ = n * p, and the standard deviation is given by σ = √(n * p * (1 - p)).
For this problem, we have n = 60 and p = 1/6. Therefore, μ = 60 * (1/6) = 10 and σ = √(60 * (1/6) * (1 - 1/6)) ≈ 2.5819.
To estimate the probability using the normal approximation, we can use the cumulative distribution function (CDF) of the normal distribution. We want to find P(X ≤ 15), where X is the number of sixes rolled.
Using R, we can calculate this probability using the pnorm() function with the parameters mean = μ and sd = σ:
pnorm(15, mean = 10, sd = 2.5819)
The true probability can be found by using the dbinom() function, which directly calculates the probability of the binomial distribution:
R
Copy code
sum(dbinom(0:15, size = 60, prob = 1/6))
By comparing the estimated probability using the normal approximation with the true probability calculated using the binomial distribution, we can assess the accuracy of the approximation.
Please note that the values obtained will depend on the specific version of R and its packages used, as well as the specific implementation details.
Learn more about probability here
https://brainly.com/question/24756209
#SPJ11
Russ, don, pamela, and stephanie are the first names of four friends who all received sports scholarships. krieger actually has a full ride, because he is a star in two different sports. use the clues to determine each person?s full name. 1. hicks and russ play on the same men?s volleyball team. 2. drake and braun have both set women?s records in swimming. 3. stephanie and drake both went to the same high school.
Answers
Russ Krieger, Don Hicks, Pamela Drake, and Stephanie Braun are the four friends who received sports scholarships. Krieger has a full ride as a star in two different sports.
Based on the given clues, we can deduce the full names of the four friends who received sports scholarships.
From clue 1, we know that Hicks and Russ play on the same men's volleyball team. Therefore, one of the friends must be Don Hicks.
From clue 2, we learn that Drake and Braun have both set women's records in swimming. Therefore, one of the friends must be Stephanie Braun.
From clue 3, it is stated that Stephanie and Drake went to the same high school. Combining this information with clue 2, we can conclude that Pamela Drake is the full name of one of the friends.
Lastly, we know that Krieger has a full ride because he is a star in two different sports. Since the other three friends have been assigned their full names, it follows that Russ Krieger is the remaining friend.
In summary, the four friends who received sports scholarships and their full names are: Russ Krieger, Don Hicks, Pamela Drake, and Stephanie Braun.
Learn more about scholarships here:
https://brainly.com/question/24291460
#SPJ11
The full names of the friends based on the provided clues are Russ Hicks, Pamela Drake, Stephanie Braun, and Don Krieger.
Explanation:The question involves a puzzle which requires using deduction and logical thinking skills to solve, typically found in mathematics problems.
Based on the clues provided:
Since Hicks and Russ play on the same men's volleyball team, this means Russ's last name must be Hicks. Hence, Russ is Russ Hicks.Stephanie and Drake both went to the same high school. Given Drake is a woman who has set records in swimming, this means Pamela must be Drake, as the name Pamela matches the female gender. Hence, Pamela is Pamela Drake.Drake and Braun have both set women's records in swimming. This clearifies that Stephanie's surname is Braun. Hence, Stephanie is Stephanie Braun.The last woman remaining is Don and she must be Don Krieger (since Krieger has a full ride scholarship for being a star in two sports).Thus, the full names of the friends are Russ Hicks, Pamela Drake, Stephanie Braun, and Don Krieger.
Learn more about Logical Deduction here:https://brainly.com/question/32226119
#SPJ12
HELP PLEASE?!!
Taking post test: exponential and logarithmic functions
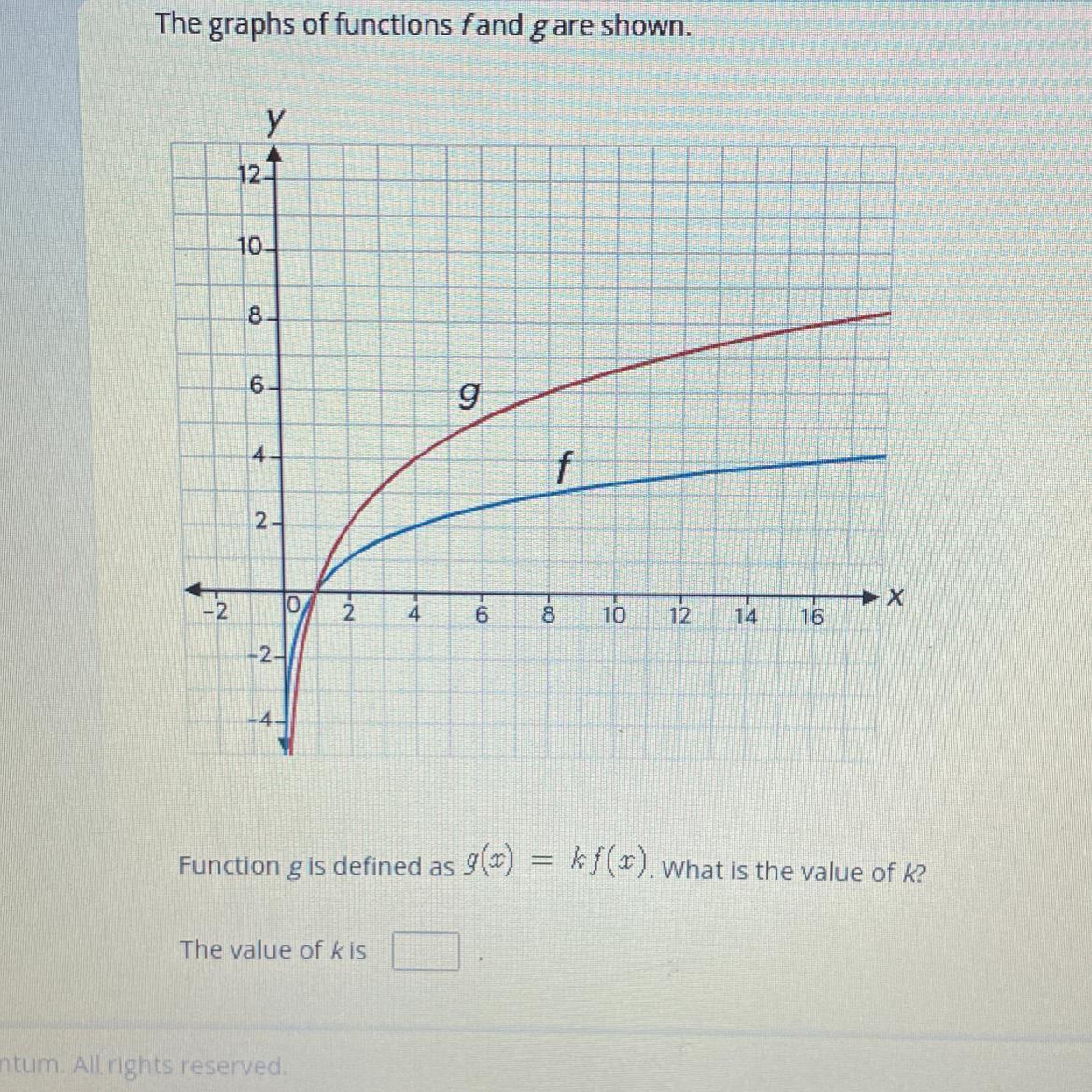
Answers
Answer:
k = 2
Step-by-step explanation:
f(2) = 1
g(2) = 2
g(x) is double of f(x)
If I1 ⊇ I2 ⊇ .... In ⊇... is a nested sequence of intervals and if In = [an; bn], show that a1 ≤ a2 ≤ ....... ≤ an ≤ ........ and b1 ≤ b2 ≤..... bn ≤ ......
Answers
The intervals are nested, each subsequent interval is contained within the previous one. Mathematically, this means I₁ ⊇ I₂ ⊇ ... In ⊇ ... . Therefore, we have:
1. I₁ ⊇ I₂ implies [a₁; b₁] ⊇ [a₂; b₂], which means a₁ ≤ a₂ and b₁ ≥ b₂.
2. I₂ ⊇ I₃ implies [a₂; b₂] ⊇ [a₃; b₃], which means a₂ ≤ a₃ and b₂ ≥ b₃.
To show that a1 ≤ a2 ≤ ... ≤ an ≤ ..., we need to use the fact that the sequence of intervals is nested, meaning that each interval is contained within the next one.
First, we know that I1 contains I2, so every point in I2 is also in I1. That means that a1 ≤ a2 and b1 ≥ b2.
Now consider I2 and I3. Again, every point in I3 is also in I2, so a2 ≤ a3 and b2 ≥ b3.
We can continue this process for all the intervals in the sequence, until we reach In. So we have:
a1 ≤ a2 ≤ ... ≤ an-1 ≤ an
and
b1 ≥ b2 ≥ ... ≥ bn-1 ≥ bn
This shows that the endpoints of the intervals are ordered in the same way.
Given that I₁ ⊇ I₂ ⊇ ... In ⊇ ... is a nested sequence of intervals and In = [an; bn], we can show that a₁ ≤ a₂ ≤ ... ≤ an ≤ ... and b₁ ≥ b₂ ≥ ... ≥ bn ≥ ... as follows:
Since the intervals are nested, each subsequent interval is contained within the previous one. Mathematically, this means I₁ ⊇ I₂ ⊇ ... In ⊇ ... . Therefore, we have:
1. I₁ ⊇ I₂ implies [a₁; b₁] ⊇ [a₂; b₂], which means a₁ ≤ a₂ and b₁ ≥ b₂.
2. I₂ ⊇ I₃ implies [a₂; b₂] ⊇ [a₃; b₃], which means a₂ ≤ a₃ and b₂ ≥ b₃.
Continuing this pattern for all intervals in the sequence, we can conclude that a₁ ≤ a₂ ≤ ... ≤ an ≤ ... and b₁ ≥ b₂ ≥ ... ≥ bn ≥ ... .
Visit here to learn more about sequence : https://brainly.com/question/30262438
#SPJ11
PLSS HELP ME WITH THIS!!

Answers
Answer:
x = -13 1/4
Step-by-step explanation:
Use cross multiplication here.
-3 x 11 = 4(x + 5)
-33 = 4x + 20
-53 = 4x
x = -53/4, or -13 1/4
Find the volume of the solid. PLEASE HELPPPPPPPP

Answers
Answer:
V≈743.25
Step-by-step explanation:
V=5
12tan(54°)ha2=5
12·tan(54°)·4·182≈743.24624
how do you solve
10^-3
Answers
Answer:
0.001
Step-by-step explanation:
Answer:
\(\frac{1}{1000}\)
Step-by-step explanation:
\(10^{-3}\)
\(= \frac{1}{10^{3}}\)
\(= \frac{1}{1000}\)
Prove the following trigonometric identity: sin 2x/ 1 - cos 2x = cot x
Answers
The trigonometric identity sin 2x/ 1 - cos 2x = cot x is proved using the trigonometric formulas
To prove the trigonometric identity, sin 2x / 1 - cos 2x = cot x
Let's write the left-hand side of the equation, sin 2x / 1 - cos 2x
Multiply the numerator and the denominator by 1 + cos 2x, (sin 2x * (1 + cos 2x))/ (1 - cos^2 2x)
Now, we know that sin 2x = 2 sin x cos x and cos^2 x + sin^2 x = 1,
Therefore, cos 2x = 2 cos^2 x - 1 and 1 - cos^2 x = sin^2 x
Hence, we can substitute cos 2x with 2 cos^2 x - 1 and 1 - cos^2 x with sin^2 x,
(2sin x cos x * (1 + 2cos^2 x - 1))/sin^2 x
Simplifying, we get, 2sin x cos x * 2cos^2 x / sin^2 x = 4cos^3 x / sin x cos x
Now, we know that cot x = cos x / sin x
Dividing both sides by cos x / sin x, we get, 4cos^3 x / sin x cos x = 4 cos x / sin x = 4 cot x
Therefore, we have proved that sin 2x / 1 - cos 2x = cot x.
Learn more about trigonometric identity:
https://brainly.com/question/7331447
#SPJ11
A room has a length of 12 metres and width of 5 metres. What is the area of the room?
Working out please
Answers
Answer:
60 sq.mStep-by-step explanation:
Given,
Length of the room = 12m
Width of the room = 5m
Therefore,
Area of the room = l × w
= 12m × 5m
= 60 sq.m (Ans)
Find the sum of the whole numbers from 1 to 870.
Answers
Answer: 378,885
Step-by-step explanation:
We could just add it all up but there is a simple easy formula :D
n(n + 1)/2 = Sum of Integers
We make n be the biggest number in the sequence. n=870 then
870(870 + 1)/2 = 378,885
Just by using a simple formula, we were able to calculate the sum very quickly.
I hope this helps!
Exponential Distributions There is a room with 20 light bulbs. The time until the bulb goes out is a random variable with an exponential distribution. They are all i.i.d. with mean 10 minutes 1. I enter the room at time 0 (i.e. all of the bulbs are on and none have burned out). What is the probability that 10 of the bulbs will burn out in the next 10 minutes. (hin start by finding the probability that a single bulb will burn out within the next 10 minutes) 2. I will begin my homework after the first bulb goes out, what is the expected amount of time until this happens. (hint: Assume that there two bulbs in the room and find the pdf for the amount of time until the first bulb goes out. Use this result to generalize.) 3. I leave the room after the last light bulb goes out. Let T denote this random variable (the time when I leave the room). Find the pdf of 1T
Answers
The probability that a single bulb will burn out within the next 10 minutes is approximately 0.6321. The expected amount of time until the first bulb goes out is 10 minutes. The probability density function (pdf) of the random variable T, representing the time when you leave the room after the last light bulb goes out, is given by \(g(t) = 20 * (1/10) * e^{(-(1/10)t)} * (1 - e^{(-(1/10)t))^(19)}\).
To find the probability that a single bulb will burn out within the next 10 minutes, we can use the exponential distribution. The exponential distribution with a mean of 10 minutes has a rate parameter λ = 1/10.
The probability density function (pdf) for an exponential distribution is given by \(f(x) = λ * e^{(-λx)}\)
In this case, we want to find the probability that a bulb burns out within the next 10 minutes, which corresponds to the cumulative distribution function (CDF) at x = 10. The CDF is given by \(F(x) = 1 - e^{(-λx)\)
So, substituting the values, we have:
\(F(10) = 1 - e^{(-(1/10)*10)\)
\(= 1 - e^{(-1)\)
= 1 - 0.3678794412
≈ 0.6321
Therefore, the probability that a single bulb will burn out within the next 10 minutes is approximately 0.6321.
The amount of time until the first bulb goes out follows an exponential distribution with a rate parameter of λ = 1/10 (since it has a mean of 10 minutes).
The probability density function (pdf) for the time until the first bulb goes out is given by\(f(t) = λ * e^{(-λt).\)
To find the expected amount of time until the first bulb goes out, we need to calculate the mean (or expected value) of this distribution.
The expected value of an exponential distribution with rate parameter λ is equal to 1/λ. In this case, the expected value is 1/(1/10) = 10 minutes.
Therefore, the expected amount of time until the first bulb goes out is 10 minutes.
To find the probability density function (pdf) of the random variable T, which represents the time when you leave the room (after the last light bulb goes out), we need to consider the distribution of the maximum of the exponential random variables.
Since there are 20 light bulbs in the room, and each follows an exponential distribution with a rate parameter λ = 1/10, the time until the last bulb goes out can be modeled as the maximum of 20 exponential random variables.
The pdf of the maximum of independent exponential random variables with the same rate parameter λ is given by \(g(t) = n * λ * e^{(-λt)} * (1 - e^{(-λt))^(n-1)}\), where n is the number of random variables.
In this case, n = 20, and λ = 1/10. Thus, the pdf of T is \(g(t) = 20 * (1/10) * e^{(-(1/10)t)} * (1 - e^{(-(1/10)t))^(19)}\)
This expression represents the pdf of the random variable T, which denotes the time when you leave the room after the last light bulb goes out.
To know more about probability,
https://brainly.com/question/24279966
#SPJ11
Madeline drew 25 hearts, 12 stars ,and 3circles .what is the ratio of stars to hearts to circles ?
Answers
The ratio of a to b to c is written as a:b:c
Then, the ratio of starts to hearts to circles is:
\(12\colon25\colon3\)Therefore, the sum of two rational numbers will
always be
Answers
Answer: Itll always be a rational number and never zero
Step-by-step explanation:
Answer:
A rational number (The third option).
Step-by-step explanation:
1. By definition, rational numbers have the following form, where and are integers and \(b\neq 0\).
2. Therefore, when you add two rational numbers, the result will be a rational number.
3. An example is shown below:
\(\frac{1}{5}+\frac{2}{5}+\frac{3}{5}\)
The result is a fraction whose numerator and denominator are integers.
(03.01 LC)
Is the following relation a function?
Х
y
-2.
1
0
3
5
5
7
8
O No
O Yes

Answers
A relation may or may not represent a function.
The given relation is a function
For a relation to be a function, each x-value must have one unique corresponding y-value
The relation can be interpreted as:
\(x \to y\)
\(-2 \to 3\)
\(0 \to -1\)
\(5 \to 8\)
\(7 \to 5\)
Notice that, each value of x have distinct corresponding y-value.
This means that, the relation satisfies the condition to be a function.
Hence, the relation is a function
Read more about functions and relations at:
https://brainly.com/question/6241820
Given: A = B,
CD LAB
Prove: CD bisects ACB
C
A
D
B

Answers
As AD = DB, CD bisects ∠ACD
In Δ ACD and ΔBCD
We need to prove that CD bisects ACB
∠A = ∠B
side AC = CB (as angle A and angle B are same)
CD is ⊥ AB
So, ∠ADC = ∠BDC
By SAS Δ ACD and ΔBCD are congurent
In congurent triangles, corresponding angles and sides are equal
So, in Δ ACD and ΔBCD
ACD = DCB
Therefore, as AD = DB, CD bisects ∠ACD
To learn more about congurency, refer here
https://brainly.com/question/2938476
#SPJ9
Complete the sentence. The intersection of three line segments can be ____.
Answers
Answer:
two points
Step-by-step explanation:
Complete the sentence. The intersection of three line segments can be two points.
Solve for ax-b=c for x
Answers
Answer:
x = \(\frac{c+b}{a}\)
Step-by-step explanation:
Given
ax - b = c ( add b to both sides )
ax = c + b ( divide both sides by a )
x = \(\frac{c+b}{a}\)
a key requirement for the process of testing hypotheses in the scientific method is
Answers
A key requirement for the process of testing hypotheses in the scientific method is experimentation. A hypothesis is an idea or explanation for a phenomenon that is grounded in existing knowledge or observations, and the scientific method involves testing those hypotheses through experimentation.
The process of testing hypotheses requires the development of a testable hypothesis, the design of experiments to test the hypothesis, and the collection and analysis of data from those experiments to evaluate the hypothesis. The experiments must be designed carefully, with appropriate controls and variables to ensure that the results are reliable and valid. Scientists also need to communicate their findings to the scientific community, which involves publishing their results in scientific journals and presenting their work at conferences.
This helps to ensure that other scientists can replicate their experiments and validate their findings, which is a critical part of the scientific process. Ultimately, the process of testing hypotheses is essential for advancing scientific knowledge and understanding how the world works.
To know more about hypotheses visit:-
https://brainly.com/question/14758286
#SPJ11
For want of a nail, the shoe was lost,
For want of a shoe, the horse was lost,
For want of a horse, the rider was lost,
For want of a rider, the battle was lost,
For want of a battle, the kingdom was lost,
And all for the want of a horseshoe nail.
From the above poem, we can deduce that the lack of one horseshoe could be either inconsequential or it could indirectly cause the loss of a war. Some systems are quite sensitive to their starting conditions, so a small change may cause a big difference in the outcome.
Keeping the above in mind, look at the following polynomials:
⦁ y = x
⦁ y = x2
⦁ y = x3
Does a slight change in the degree of the polynomials affect their graphs? If yes, show your results graphically, taking values of x as -3, -2, -1, 0, 1, 2 and 3 in every case.
Answers
The poem For Want of a Nail is a warning about how small things can have large and unforeseen consequences. The lack of a horseshoe could lead to the loss of a horse, which could result in the loss of a rider, which could lead to the loss of a battle.
This shows that a small change can cause a big difference in the outcome. We can see a similar phenomenon in the world of mathematics, where small changes in a function can lead to significant changes in its behavior. For example, the degree of a polynomial can have a dramatic effect on its graph. Let's consider the function y = x². This is a second-degree polynomial, which means that its graph is a parabola. If we change the degree of this polynomial to 1, then we get the function y = x, which is a straight line. If we change the degree of this polynomial to 3, then we get the function y = x³, which is a cubic curve. If we graph these functions for the values of x from -3 to 3, we can see how the slight change in the degree of the polynomial affects their graphs. The graph of y = x² is a parabola that opens upward. TThe graph of y = x is a straight line that passes through the origin. The graph of y = x³ is a cubic curve that passes through the origin and has two turning points. These graphs show that a small change in the degree of the polynomial can have a significant effect on its graph.For such more question on polynomial
https://brainly.com/question/4142886
#SPJ8