Question 9 Multiple Choice Worth 1 points)
(04.01 LC)
Segment AB has point A located at (8, 9). If the distance from A to B is 10 units, which of the following could be used to calculate the coordinates for point B
Answers
Answer: \(\bold{10 = \sqrt {\left( {x- 8 } \right)^2 + \left( {y - 9 } \right)^2 }}\)
Step-by-step explanation:
Given:
The coordinates of Point A: (8, 9)
The coordinates of Point B are unknown: (x, y)
The distance from A to B is 10 units
Then, using the distance formula:
\(AB = \sqrt {\left( {x- 8 } \right)^2 + \left( {y - 9 } \right)^2 }\)
Therefore,
\(10 = \sqrt {\left( {x- 8 } \right)^2 + \left( {y - 9 } \right)^2 }\)
Related Questions
WILL MARK BRAINLIEST!!
1. Find 7% sales tax on a $48 purchase.
2. Find 6.5% sales tax on a $25 purchase.
3. You markup a $25 tool by 45%. What is the new price?
4. You markup a $40 watch by 75%. What is the new price?
5. You discount a $120 TV by 44%. What is the new price?
6. You discount a $65 coat by 25%. What is the new price?
PLEASE EXPLAIN HOW THAT ANSWER IS CORRECT, PLEASE HURRY! I NEED THIS FILLED OUT ASAP.
Answers
Answer/Explanation:
1. 48 x 0.07 = $3.36
2. 25 x 0.065 = $1.63
3. 25 x 0.45 = 11.25, 11.25 + 25 = $36.25 (New price is $36.25)
4. 40 x 0.75 = 30, 30 + 40 = $70
(New price is $70)
5. 120 x 0.44 = 52.80, 120 - 52.80 = 67.2 (New price is $67.20)
6. 65 x 0.25 = 16.25, 65 - 16.25 = 48.75
(New price is $48.75)
Hope this helps :)
Assume that the sample is a random sample from a distribution that is reasonably normally distributed and that we are doing inference for a population mean. Find the area in a t-distribution to the right of 2.6 if the sample has size n
Answers
The area to the right of 2.6 in a t-distribution with n degrees of freedom is 0.9082, assuming the sample is a random sample from a distribution that is reasonably normally distributed and that we are doing inference for a population mean.
We can use a t-distribution table or a statistical software program to find the area to the right of 2.6. Here, I'll show you how to use a t-distribution table:
Determine the degrees of freedom (df) for the t-distribution. This is equal to n - 1.
Look up the t-value that corresponds to a one-tailed probability of 0.05 and df.
Multiply the t-value by -1 to get the positive value for the right tail. In other words, we need the value for the right tail, so we flip the sign of the t-value.
Add 0.5 to the result to account for the area to the left of 2.6. This gives us the cumulative probability from negative infinity to 2.6.
Subtract the result from 1 to get the area to the right of 2.6.
For example, suppose we have a sample of size n = 10. Then, the degrees of freedom for the t-distribution would be df = 10 - 1 = 9. Using a t-distribution table, we can look up the t-value that corresponds to a one-tailed probability of 0.05 and df = 9:
t-value = 1.833
Since we need the positive value for the right tail, we multiply by -1 to get:
t-value = -1.833
Adding 0.5 to account for the left tail gives:
t-value + 0.5 = -1.333
Finally, subtracting this result from 1 gives us the area to the right of 2.6:
Area to the right of 2.6 = 1 - 0.0918 = 0.9082
for such more question on t-distribution
https://brainly.com/question/16994704
#SPJ11
PLEASE I NEED FAST
X
Y
Z
find the value of missing variables

Answers
Answer:
.................... .

The equation 10x +5y= 80 where x is the number of sandwiches models the problem in the Solve lt . How many sandwiches can you buy if you buy 3 pizzas? 6 pizzas?
Answers
Given:
\(10x+5y=80\)Here x represents the number of pizzas and y represents the number of sandwiches.
Buy 3 pizas:
Substitute x=3 in the given expression, and solve for y.
\(\begin{gathered} 10x+5y=80 \\ 10\times3+5y=80 \\ 5y=80-10\times3 \\ y=\frac{80-30}{5} \\ y=\frac{50}{5} \\ y=10 \end{gathered}\)Thus, you can buy 10 sandwiches if you buy 3 pizza.
Assume you buy 6 pizzas.
Substitute x=6 in the given expression.
\(\begin{gathered} 10x+5y=80 \\ 10\times6+5y=80 \\ 5y=80-10\times6 \\ y=\frac{80-60}{5} \\ y=\frac{20}{5} \\ y=4 \end{gathered}\)Thus, you can buy 4 sandwiches if you buy 6 pizzas.
Determine if the data is skewed or symmetric.

Answers
Answer:
skewed
Step-by-step explanation:
what is the slope of the line that contains the points (-2,6) and (2,-2)
Answers
Answer:
\(-\frac{8}{4}\)
Step-by-step explanation:
To find slope from 2 points: \(\frac{y2-y1}{x2-x1}\)
\(\frac{-2-6}{2-(-2)} =-\frac{8}{4}\)
The proportion of a normal distribution located between z = .50 and z = -.50 is ____.
Answers
The proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
We have,
A normal distribution located between z = 0.50 and z = -0.50,
So,
Now,
From the Z-score table,
We get,
The Probability corresponding to the Z score of -0.50,
i.e.
P(-0.50 < X < 0) = 0.191,
And,
The Probability corresponding to the Z score of -0.50,
i.e.
P(0 < X < 0.50) = 0.191,
Now,
The proportion of a normal distribution,
i.e.
P(Z₁ < X < Z₂) = P(Z₁ < X < 0) + P(0 < X < Z₂)
Now,
Putting values,
i.e.
P(-0.50 < X < 0.50) = P(-0.50 < X < 0) + P(0 < X < 0.50)
Now,
Again putting values,
We get,
P(-0.50 < X < 0.50) = 0.191 + 0.191
On solving we get,
P(-0.50 < X < 0.50) = 0.382
So,
We can write as,
P(-0.50 < X < 0.50) = 38.2%
So,
The proportion of a normal distribution is 38.2%.
Hence we can say that the proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
Learn more about normal distribution here
https://brainly.com/question/13759327
#SPJ4
102 = V - 66
Addition and subtraction equation practice
Answers
Answer:
\(V=168\)
Step-by-step explanation:
\(Here,102=V-66\)
\(102+66=V\)
\(168=V\)
Sorry If it is wrong.....
see the attachment

Solve the following system of equations.
– 7x-6v = 15
3x + 5y = -4
Answers
Answer:
yup umm
Step-by-step explanation:
-4
this time I cannot tell what the answer is

Answers
Answer:
Its the first one
Step-by-step explanation:
Some help... just 1 answer would be utmost appreciated! <3

Answers
Answer: I think that it is BD = 46
Step-by-step explanation: sorry if that is incorrect tryed this for like 30 min
A figure has been shrunk from center O with a scale factor r = 0.25. What scale factor would enlarge the figure back to the original size?
r =
Answers
Answer:
.75
Step-by-step explanation:
which is greater, 1.349 > 1.11
Answers
Answer:
that is right the greater one is 1.349
Step-by-step explanation:
bc the number after the decimal 3 is bigger than 1
Which of the following is equivalent to 8(5f – 7) + 3f
A- 40f – 7 +3f
B- 43f – 7
C- –13f
D- 43f – 56
Answers
2) A-5=62 PLSSSS HELLPPP
Answers
Answer:
Step-by-step explanation:
a-5=62 add 5 to both sides
a=67
Refer to the right triangle shown.

Answers
Answer:
1/2 of an answer is zero answer.
Step-by-step explanation:
Answer:
a. Solve for x. x=16
b. The lenght of the missing side is 10 units.
Step-by-step explanation:
a.
x-6>0 x>6
According to the Pythagorean theorem: a²+b²=c².
Hence,
\((x-6)^2+24^2=26^2\\x^2-2*x*6+6^2+24*24=26*26\\x^2-12x+6*6+576=676\\x^2-12x+36+576-676=676-676\\x^2-12x-64=0\\x^2-12x-4x+4x-64=0\\x^2-16x+4x-64=0\\(x*x-16x)+(4x-64)=0\\x*(x-16)+4*(x-16)=0\\(x-16)*(x+4)=0\\x-16=0\\x_1=16\\x+4=0\\x_2=-4\notin\\\)
b.
\(16-6=\\10\)
PLEASE help me asap what is the answer to this

Answers
Answer:
TUVW
Step-by-step explanation:
bobby continues shooting three targets until he knocks all of them down. the probability of hitting a target is p. find the probability that bobby will require exactly 5 shots to accomplish the goal.
Answers
The probability that Bobby will require exactly 5 shots to knock down all three targets is p^3 * (1-p)^2.
1. Bobby must hit the first three targets in order to knock them down. The probability that he will hit the first three targets is p^3.
2. After hitting the first three targets, Bobby must miss the fourth shot in order to require 5 shots to accomplish the goal. The probability that he will miss the fourth shot is (1-p).
3. Bobby must hit the fifth shot in order to knock all three targets down. The probability that he will hit the fifth shot is p.
4. Therefore, the probability that Bobby will require exactly 5 shots to knock down all three targets is p^3 * (1-p)^2.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
The length of a rectangular poster is 10 more inches than three times its width. The area of the poster is 88 square inches. Solve for the dimensions (length and width) of the poster.
The dimensions are ___ inches by___ inches.
Answers
Let's assume that the width of the poster is "x" inches.
According to the problem, the length of the poster is 10 more inches than three times its width. So, the length is (3x + 10) inches.
The area of a rectangle is given by the formula A = length x width. We are given that the area of the poster is 88 square inches. So, we can write:
(3x + 10) x x = 88
Simplifying the above equation, we get:
3x^2 + 10x - 88 = 0
We can solve this quadratic equation by factoring or using the quadratic formula. Let's use the quadratic formula:
x = [-b ± sqrt(b^2 - 4ac)] / 2a
where a = 3, b = 10, and c = -88
Plugging in the values, we get:
x = [-10 ± sqrt(10^2 - 4(3)(-88))] / 2(3)
x = [-10 ± sqrt(1000)] / 6
x = [-10 ± 31.62] / 6
x = 3.27 or x = -8.94
Since the width cannot be negative, we ignore the negative solution. Therefore, the width of the poster is approximately 3.27 inches.
Using this value, we can find the length:
length = 3x + 10 = 3(3.27) + 10 = 19.81 inches (rounded to two decimal places)
Therefore, the dimensions of the poster are approximately 3.27 inches by 19.81 inches.
Answer:
It's just 22
Step-by-step explanation:
22
Based on the diagram below, we can say that the two triangles ___.

Answers
Solution
Step1
The AA criterion for triangle similarity states that if two triangles have two pairs of congruent angles, then the triangles are similar.
Step2
Two pairs angles are equal, hence they are similar
Answer
Are similar by AA
-53 = 7x -4
explain/show ur work
Answers
Answer:
-7
Step-by-step explanation:
-53 = 7x - 4
Add:
-53 = 7x - 4
+4 +4
------------------
-49 = 7x
---- -----
7 7
-7 = x
Hope this helped.
-7x=-4+53
-7x=49
X=49÷7
X=-7
urn a contains six white balls and seven black balls. urn b contains five white balls and three black balls. a ball is drawn from urn a and then transferred to urn b. a ball is then drawn from urn b. what is the probability that the transferred ball was white given that the second ball drawn was white?
Answers
Using the Bayes' theorem, we find the probability that the transferred ball was white given that the second ball drawn was white to be 52/89, or approximately 0.5843.
To solve this problem, we can use Bayes' theorem, which relates the conditional probability of an event A given an event B to the conditional probability of event B given event A:
P(A|B) = P(B|A) * P(A) / P(B)
where P(A|B) is the probability of event A given that event B has occurred, P(B|A) is the probability of event B given that event A has occurred, P(A) is the prior probability of event A, and P(B) is the prior probability of event B.
In this problem, we want to find the probability that the transferred ball was white (event A) given that the second ball drawn was white (event B). We can calculate this probability as follows:
P(A|B) = P(B|A) * P(A) / P(B)
P(B|A) is the probability of drawing a white ball from urn b given that the transferred ball was white and is now in urn b. Since there are now six white balls and three black balls in urn b, the probability of drawing a white ball is 6/9 = 2/3.
P(A) is the prior probability of the transferred ball being white, which is the number of white balls in urn a divided by the total number of balls in urn a, or 6/13.
P(B) is the prior probability of drawing a white ball from urn b, which can be calculated using the law of total probability:
P(B) = P(B|A) * P(A) + P(B|not A) * P(not A)
where P(B|not A) is the probability of drawing a white ball from urn b given that the transferred ball was black and P(not A) is the probability that the transferred ball was black, which is 7/13.
To calculate P(B|not A), we need to first calculate the probability of the transferred ball being black and then the probability of drawing a white ball from urn b given that the transferred ball was black.
The probability of the transferred ball being black is 7/13. Once the transferred ball is moved to urn b, there are now five white balls and four black balls in urn b, so the probability of drawing a white ball from urn b given that the transferred ball was black is 5/9.
Therefore, we can calculate P(B) as follows:
P(B) = P(B|A) * P(A) + P(B|not A) * P(not A)
= (2/3) * (6/13) + (5/9) * (7/13)
= 89/117
Now we can plug in all the values into Bayes' theorem to find P(A|B):
P(A|B) = P(B|A) * P(A) / P(B)
= (2/3) * (6/13) / (89/117)
= 52/89
Therefore, the probability that the transferred ball was white given that the second ball drawn was white is 52/89, or approximately 0.5843.
To know more about Bayes' theorem refer here :
https://brainly.com/question/29598596#
#SPJ11
Find the equation of the axis of symmetry and the coordinates of the vertex of the graph of the following function. y= -3x^2^ -12x-3
Answers
Answer:
\(y = - 3x {}^{ - 12x - 1} \)
Step-by-step explanation:
Hope that's help your answer
What is the highest common factor of 30 and 132?
Answers
Answer:
6
Step-by-step explanation:
hope this helps
2y+7x=-5 what does y and x equal
Answers
Answer:
There is no value of x and y.
Step-by-step explanation:
To solve the equation 2y + 7x = -5 for y and x, we can use the following steps:
1.
Isolate y on one side of the equation by subtracting 7x from both sides:
2y = -7x - 5
2.
Divide both sides by 2 to get y by itself:
y = (-7/2)x - (5/2)
3.
To find x, we can substitute the value of y we just found into the original equation:
2(-7/2)x + 7x = -5
4.
Simplify and solve for x:
-7x + 7x = -5
0 = -5
Since this equation has no solution, there is no value of x and y that will satisfy it.
An ellipse or hyperbola uses the general form ax2+cy2+dx+ey+f=0. solving for 5 unknowns (a, b, c, d, e, f) requires 5 equations, needs 5 points given. but if one of the coefficients is divided out (a or c), then only 4 coefficients remain and only 4 points are needed. x2+cy2+dx+ey+f=0 given 4 points on a vertical ellipse (3.75, 0), (0, 2.71), (1, -7), and (-1, -5.725). select the missing coefficients (answers have been rounded to the nearest tenth).
Answers
the missing coefficients are approximately c = 0.5, d = 0.7, e = -1.6, and f = -9.9.
To determine the missing coefficients in the equation x² + cy² + dx + ey + f = 0, we can use the given points on a vertical ellipse and substitute them into the equation. This will create a system of equations that we can solve to find the values of c, d, e, and f.
Let's substitute the given points into the equation:
For the point (3.75, 0):
(3.75)² + c(0)² + d(3.75) + e(0) + f = 0
14.06 + 3.75d + f = 0 -- Equation 1
For the point (0, 2.71):
(0)² + c(2.71)² + d(0) + e(2.71) + f = 0
7.35c + 2.71e + f = 0 -- Equation 2
For the point (1, -7):
(1)² + c(-7)² + d(1) + e(-7) + f = 0
1 + 49c + d - 7e + f = 0 -- Equation 3
For the point (-1, -5.725):
(-1)² + c(-5.725)² + d(-1) + e(-5.725) + f = 0
1 + 32.86c - d - 5.725e + f = 0 -- Equation 4
We now have a system of equations with four variables (c, d, e, f). By solving this system, we can find the missing coefficients.
Solving the system of equations using a numerical solver or by hand, we find the following approximate values:
c ≈ 0.5
d ≈ 0.7
e ≈ -1.6
f ≈ -9.9
Therefore, the missing coefficients are approximately c = 0.5, d = 0.7, e = -1.6, and f = -9.9.
Learn more about Equation here
https://brainly.com/question/25300779
#SPJ4
For any positive numbers a,b, and d, with b=1, logb a+logb d=
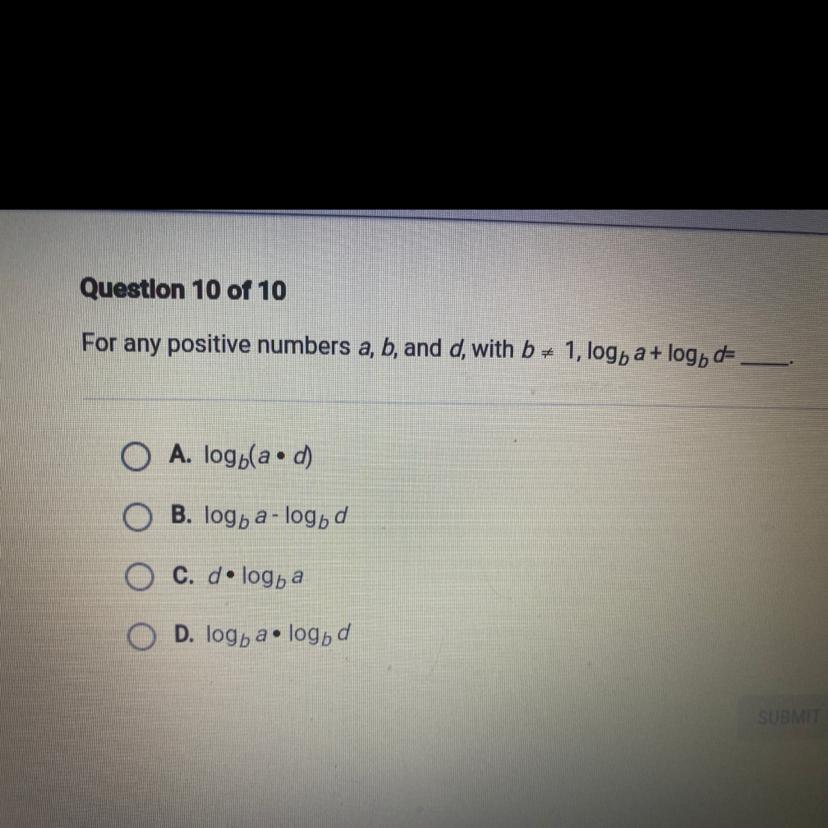
Answers
Answer the right answer is a
A can do a piece of work in 10 days, and b can do the same work in 20 days. With the help of c, they finished the work in 4 days. C can do the work in how many days, working alone?.
Answers
C can finish the work in 5 days, working alone.
Let C alone take x days to complete the work.
The following points should be kept in mind when approaching the solution of this problem :
Step 1: Find the work done by A alone in 1 day and that done by B alone in 1 day.
Step 2: Use the work done by A alone in 1 day and that done by B alone in 1 day to find the work done by all three A, B, and C together in 1 day.
Step 3: Use the work done by all three A, B, and C together in 1 day to find the number of days it takes for C to complete the job alone.
Now let's begin:
Step 1: Let A alone take 10 days to complete the job.
So, A alone can do the job in 1 day = 1/10.
Let B alone take 20 days to complete the job.
So, B alone can do the job in 1 day = 1/20.
Step 2: Now we can find the work done by A, B, and C together in 1 day. We know that they finish the job in 4 days, so the total work done = 1/4.
The work done by A alone in 1 day = 1/10.
The work done by B alone in 1 day = 1/20.
Let C alone do the job in 1 day = 1/x.
Total work done in 1 day by A, B, and C = 1/10 + 1/20 + 1/x = 2/20 + 1/x = 1/4.
We can now simplify the equation: 1/x = 1/4 - 2/20 = 1/5.
x = 5
Therefore, C alone can do the work in 5 days, working alone.
Learn more about working problems:
https://brainly.com/question/31734896
#SPJ11
Assume the following cash flows and calculate the IRR
-865000 ( T0)
315,000 (T1)
-25,000 (T2)
605,000 (T3)
27,000 (T4)
Calculate the risk-adjust
Answers
The investment is expected to generate an annualized return of 13.5%.
To calculate the IRR of the given cash flows, we need to find the discount rate that equates the present value of all the cash inflows and outflows. Let's break down the calculations step by step:
Assign a negative sign (-) to cash outflows and a positive sign (+) to cash inflows. This convention helps distinguish between the two types of cash flows.
The given cash flows are:
T0: -865,000
T1: +315,000
T2: -25,000
T3: +605,000
T4: +27,000
Set up the equation for the IRR calculation. The IRR equation is derived from the NPV formula, where the NPV is set to zero.
0 = -865,000 + (315,000 / (1 + IRR)¹) - (25,000 / (1 + IRR)²) + (605,000 / (1 + IRR)³) + (27,000 / (1 + IRR)⁴)
Solve the equation to find the IRR. Unfortunately, finding the exact IRR through manual calculations can be challenging. However, we can use computational tools like Excel or financial calculators to find an approximate value. These tools use numerical methods to solve complex equations.
Using a financial calculator or Excel, the IRR for the given cash flows is approximately 13.5%.
To know more about IRR here
https://brainly.com/question/31393609
#SPJ4
A shopper pays $612 for a $600 swing set after sales tax is added. What is the sales tax percentage?
Answers
Answer:
proofs attached to answer
Step-by-step explanation:
proofs attached to answer
