Question 4 of 10
Which situation best illustrates the concept of absolute advantage?
A. A German factory can build more sports cars than foreign factories.
B. Most of the world's largest companies have operations in many different countries.
C. The total value of Japanese imports is greater than the total value of the country's exports.
D. A French restaurant buys food from nearby farms to support the local economy.

Answers
Situation which illustrates best the concept of absolute advantage is: Option A - A German factory can build more sports cars than foreign factories.
Absolute advantage is the potential of an individual, a company, or a country to produce a higher quantity of output than its competitors while using the same inputs. It means an institution with absolute advantage has more efficiency in producing a particular commodity than its rivals. It utilizes lower marginal cost (materials and labor), making its output much cheaper than others.
A factory in German has an absolute advantage because it can produce more sports car than foreign countries. Absolute advantage makes the factory more competitive in the market than its rivals.
Therefore, the correct answer is option A.
Learn more about absolute advantage here :-
https://brainly.com/question/27956614
#SPJ4
Related Questions
What is the area of a triangle
Answers
Answer:A=BxH divided by 2
_
Step-by-step explanation:
7. Suppose we are interested in comparing the average years of service accountants have between males and females to see if there is a significant difference between the genders and how long they have stayed in their current job. The following data is provided:
Answers
The 99% confidence interval for the difference between the average years of service between men and women would be = 3.43.
What is confidence intervals?Confidence interval is defined as the statistical parameter that is used to know if a set of values would fall within a certain range of population or not.
Using the statistical table, the value of 99% or 0.99 confidence interval has a z-score = 2.576
The standard error that exists between the bothe value = SD/Ö
Where SD = difference between the standard deviations = 8.39 - 4.39 = 4
Where ñ = different between the average years of service = 9.62
Standard error= 4/√9.62 = 4/3.01 = 1.33
The confidence interval = 2.576 × 1.33 = 3.43.
Learn more about confidence interval here:
https://brainly.com/question/26658887
#SPJ1

Convert: 8 tons = _____ pounds
A. 80 pounds
B. 4 pounds
C. 16,000 pounds
D. 8,000 pounds
Answers
8 tons = 16000 pounds
conversion:
1 tons ➟ 2000 pounds
8 tons ➟ (2000 * 8) pounds
8 tons ➟ 16000 pounds ⚡⚡
The amount 8 tons in pounds can be written as 16, 000 pounds.
To convert 8 tons to pounds,
we need to know that 1 ton is equal to 2,000 pounds.
We know that when a smaller unit converted to big unit then we have to multiply.
So, the conversion of 8 tons to pounds
= 8 tons x 2,000 pounds/ton
= 16,000 pounds
Thus, the amount 8 tons in pounds can be written as 16, 000 pounds.
Learn more about Unit Conversion here:
https://brainly.com/question/14523259
#SPJ6
helllllllppppp plzzz

Answers
Answer:
Answer D) B, C, and D
Step-by-step explanation:
Point D is 2 and point B is -2, meaning they are opposites of each other. Point C is 0, which is it's own opposite
The rabbit population in a forest area grows at the rate of 9% monthly. If there are 242 rabbits in September, find how many rabbits (rounded to the nearest whole number) should be expected next September. Use
y
=
242
(
2.7
)
0.09
t
y
=
242
(
2.7
)
0.09
t
Answers
Answer:
503 should be the answer
Step-by-step explanation:
Answer:
i think its 503
Step-by-step explanation:
242 multiplied by 0.09 = 21.78
21.78 multiplied by 12 = 261.36
added by 242 = 503.36
factorise:x^3-(y-z)^3
Answers
The factorized form of \(x^3 - (y - z)^3\ is \ (x - y + z)(x^2 - xy + 2xz + yz - 2z^2).\)
The Factorization is derived from the application of a mathematical identity. As an AI language model, the information provided is generated based on existing knowledge and formulas.
The given expression is \(x^3 - (y - z)^3.\)To factorize it, the difference of cubes, which states that a^3 - b^3 can be factorized as\((a - b)(a^2 + ab + b^2).\)
Applying this identity to our expression, we have:
\(x^3 - (y - z)^3 = (x - (y - z))((x - (y - z))^2 + (x - (y - z))(y - z) + (y - z)^2)\)
Simplifying further, we get:
\(= (x - y + z)(x^2 - 2xy + 2xz - y^2 + 2yz - z^2 + xy - y^2 + yz - z^2 + y^2 - 2yz + z^2)\\= (x - y + z)(x^2 - 2xy + xy + 2xz + yz - 2yz - y^2 + y^2 - y^2 + 2yz - 2z^2 + y^2 - z^2 + z^2)\\= (x - y + z)(x^2 - xy + 2xz + yz - 2z^2)\)
So, the factorized form of \(x^3 - (y - z)^3 \ is\ (x - y + z)(x^2 - xy + 2xz + yz - 2z^2).\)
the above factorization is derived from the application of a mathematical identity.
To know more about factorized .
https://brainly.com/question/14268870
#SPJ11
Model the data in the table with a linear equation
in slope-intercept form. Then tell what the slope and y-intercept
represent.
Write the linear equation in slope-intercept form.
y =
(Use integers or decimals for any numbers in the expression.)
Time Worked, Wages Earned
x (h)
1
3
6
9
y (S)
8.00
24.00
48.00
72.00
Answers
The data in the table can be modeled by this linear equation in slope-intercept form: y = 8x - 5.
The slope is 8, which means the wages earned increases at rate of 8 dollars per hour as the time increases.
The y-intercept is -5 and it represent the initial wages earned.
How to determine an equation of this line?In Mathematics and Geometry, the slope-intercept form of the equation of a straight line is represented by this mathematical expression;
y = mx + c
Where:
m represent the gradient, slope, or rate of change.x and y represent the data points.c represent the vertical intercept.First of all, we would determine the slope of this line;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (24.00 - 8.00)/(3 - 1)
Slope (m) = 16.00/2
Slope (m) = 8
At data point (1, 3), a linear equation in slope-intercept form for this line can be calculated as follows:
y - y₁ = m(x - x₁)
y - 3 = 8(x - 1)
y = 8x - 8 + 3
y = 8x - 5
Read more on slope here: https://brainly.com/question/20282417
#SPJ1
I'm so lost on this work

Answers
Answer:
Typist A can type faster
Step-by-step explanation:
Replace the t in w = 50t with any numbers and graph the points you get
You can see that typist A can type 50 words per minute when typist B can only type 40
BRAINLIEST!!!!!!!!!!

Answers
1450(.88)^22 = 87.1 = 87
Plug { 22 } into { t }
he roots of the function f(x) = x2 – 2x – 3 are shown. What is the missing number?
x = –1 and x =
Answers
Please help!!!!!!!!!!!!!

Answers
Answer:
37, 3, 37
Step-by-step explanation:
Let f(x) = 2x^4 -3x^2 and g(x) = 6x^2 -5x+2What is the rule for ( f - g ) (x)?
Answers
ANSWER
(f - g)(x) = 2x⁴ - 9x² + 5x - 2
EXPLANATION
To subtract two functions:
\((f-g)(x)=f(x)-g(x)\)We have to replace each function with its expression:
\(f(x)-g(x)=(2x^4-3x^2)-(6x^2-5x+2)\)And add like terms:
\(\begin{gathered} f(x)-g(x)=2x^4-3x^2-6x^2+5x-2 \\ f(x)-g(x)=2x^4-9x^2+5x-2 \end{gathered}\)Determine a series of transformations that would map Figure J onto Figure K. J
Figure.
Figure

Answers
Figure J is rotated 90° clockwise and then translated by 3 units toward the right.
What is a transformation of a shape?A point, line, or mathematical figure can be converted in one of four ways, and each has an effect on the object's structure and/or position.
Rotation does not change the shape and size of the geometry. But changes the orientation of the geometry.
The translation does not change the shape and size of the geometry. But changes the location.
Figure J is rotated 90° clockwise and then translated by 3 units toward the right.
More about the transformation of the shape link is given below.
https://brainly.com/question/27224339
#SPJ1
Find the sum of the first 10 terms of the arithmetic sequence: 5, 12, 19, 26, ...
Answers
ANSWER
S₁₀ = 365
EXPLANATION
The sum of the first n terms of an arithmetic sequence is called the arithmetic series formula, given by,
\(S_n=\frac{n(a_1+a_n)}{2}\)In this sequence, we can see that a₁ = 5, and the sum we have to find is the sum of the first 10 terms, so n = 10. To find the sum, we have to find the term a₁₀ first.
The nth term of an arithmetic sequence is given by the formula,
\(a_n=a_1+d(n-1)\)Where d is the common difference. To find this formula for this sequence, we have to find the common difference by using any of the given terms. If we use n = 2 - in other words, we write it for a₂,
\(a_2=12=5+d(2-1)\)Solving for d,
\(\begin{gathered} 12=5+d \\ d=12-5=7 \end{gathered}\)Thus, the formula for the nth term of this sequence is,
\(a_n=5+7(n-1)\)And the 10th term is,
\(a_{10}=5+7(10-1)=5+7\cdot9=5+63=68\)So, the sum of the first 10 terms is,
\(S_{10}=\frac{10(5+68)}{2}=\frac{10\cdot73}{2}=\frac{730}{2}=365\)Hence, the sum of the first 10 terms of this arithmetic sequence is 365.
Enter the ordered pair for the vertices for (Ry-axis T(2, 0))(QRST).
I need help with this please help me

Answers
Answer:
Q'(-3, 5)R'(-5, -1)S'(-2, 0)T'(0, 3)Step-by-step explanation:
You want the coordinates of the vertices of QRST after it has been translated right 2 units, then reflected across the y-axis. The original coordinates are Q(1, 5), R(3, -1), S(0, 0), T(-2, 3).
Composition of TransformationsThe problem statement is written as a composition of the transformations Ry and T(2,0). A composition of functions is generally executed right to left, meaning the translation will be done first, then the reflection.
TranslationThe numbers in the translation vector are added to the coordinates:
(x, y) ⇒ (x+2, y+0)
ReflectionReflection over the y-axis changes the sign of the x-coordinate:
(x, y) ⇒ (-x, y)
ApplicationThen the composition of transformations is ...
(x, y) ⇒ (-(x+2), y)
Q(1, 5) ⇒ Q'(-3, 5)
R(3, -1) ⇒ R'(-5, -1)
S(0, 0) ⇒ S'(-2, 0)
T(-2, 3) ⇒ T'(0, 3)
If 46 people can fit into 64 square teet. Which proportion should you use to estimate how many people are in a 600
square foot area?
Answers
Answer:
431.25 approximately 431
Step-by-step explanation:
one way of calculating it would be to get the measure per one person which would be equal to 46 / 64 = 0.7 people in one square feet
then multiply 0.7 by the total distance = 431.25 approximated to 431
Melanie goes to a shelter to buy a dog. She has settled on two dogs, an Alsatian and a bulldog. To decide between them, she plans to flip a coin. Before she does, she flips the coin 50 times to check for fairness of the model. Her results are shown in the table.
Coin Toss Result Times Result Occurred
heads 24
tails 26
The relative frequency of landing on heads is ____. The relative frequency of landing on tails is
____.
Answers
Using it's concept, it is found that the relative frequency of landing on heads is 0.48 and of landing on tails is 0.52.
What is a relative frequency?A relative frequency is given by the number of desired outcomes divided by the number of total outcomes.
In this problem, out of 50 flips, 24 landed on heads and 26 on tails, hence:
Fh = 24/50 = 0.48.
Ft = 26/50 = 0.52.
The relative frequency of landing on heads is 0.48. The relative frequency of landing on tails is 0.52.
More can be learned about relative frequency at https://brainly.com/question/23359601
How to do an equation like this step by step? 4.5 (8 - x) + 36 = 100 - 2.5 (3x + 24)
Answers
Answer:
x = -10.6667
Step-by-step explanation:
Solve for x:
4.5 (8 - x) + 36 = 100 - 2.5 (3 x + 24)
4.5 (8 - x) = 36 - 4.5 x:
36 - 4.5 x + 36 = 100 - 2.5 (3 x + 24)
Grouping like terms, -4.5 x + 36 + 36 = (36 + 36) - 4.5 x:
(36 + 36) - 4.5 x = 100 - 2.5 (3 x + 24)
36 + 36 = 72:
72 - 4.5 x = 100 - 2.5 (3 x + 24)
-2.5 (3 x + 24) = -7.5 x - 60:
72 - 4.5 x = -7.5 x - 60 + 100
Grouping like terms, -7.5 x - 60 + 100 = (100 - 60) - 7.5 x:
72 - 4.5 x = (100 - 60) - 7.5 x
100 - 60 = 40:
72 - 4.5 x = 40 - 7.5 x
Add 7.5 x to both sides:
7.5 x - 4.5 x + 72 = (7.5 x - 7.5 x) + 40
7.5 x - 7.5 x = 0:
7.5 x - 4.5 x + 72 = 40
Grouping like terms, 7.5 x - 4.5 x + 72 = (-4.5 x + 7.5 x) + 72:
(-4.5 x + 7.5 x) + 72 = 40
7.5 x - 4.5 x = 3 x:
3 x + 72 = 40
Subtract 72 from both sides:
3 x + (72 - 72) = 40 - 72
72 - 72 = 0:
3 x = 40 - 72
40 - 72 = -32:
3 x = -32
Divide both sides of 3 x = -32 by 3:
(3 x)/3 = (-32)/3
3/3 = 1:
x = (-32)/3
(-32)/3 = -10.6667:
Answer: x = -10.6667
if f(x) is continuous on a closed interval [a,b], then f(x) must attain an absolute minimum and an absolute maximum on the interval [a,b]
Answers
Yes, if a function f(x) is continuous on a closed interval [a,b], then it must attain an absolute minimum and an absolute maximum on the interval [a,b].
The reason for this is that the intermediate value theorem states that if f(x) is continuous on a closed interval [a,b] and y is any value between f(a) and f(b), then there exists a number c in the interval (a,b) such that f(c) = y. This means that for any value y between the minimum and maximum values of f(x) on the interval [a,b], there is at least one x-value in the interval where f(x) is equal to y. Therefore, since f(x) can take on any value between its minimum and maximum values, it must attain both an absolute minimum and an absolute maximum on the interval [a,b].
To know more about interval
https://brainly.com/question/13708942
#SPJ4
Find each. a. za_2 for the 99% confidence interval b. za_2 for the 98% confidence interval c. za_2 for the 95% confidence interval d. za_2 for the 90% confidence interval e. za_2 for the 94% confidence interval
Answers
Answer:
a) Z = 2.575.
b) Z = 2.327.
c) Z = 1.96.
d) Z = 1.645.
e) Z = 1.88.
Step-by-step explanation:
Question a:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.99}{2} = 0.005\)
Now, we have to find z in the Z-table as such z has a p-value of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.005 = 0.995\), so Z = 2.575.
Question b:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.98}{2} = 0.01\)
Now, we have to find z in the Z-table as such z has a p-value of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.01 = 0.99\), so Z = 2.327.
Question c:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.95}{2} = 0.025\)
Now, we have to find z in the Z-table as such z has a p-value of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.025 = 0.975\), so Z = 1.96.
Question d:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.9}{2} = 0.05\)
Now, we have to find z in the Z-table as such z has a p-value of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.05 = 0.95\), so Z = 1.645.
Question e:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.94}{2} = 0.03\)
Now, we have to find z in the Z-table as such z has a p-value of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.03 = 0.97\), so Z = 1.88.
Katie earns $0.50 each time she does a chore. She does some chores. Then she gets $6 for her birthday. How much money does she have?
Answers
Answer:
First I need to know how much chores she does because I can't get the money that she makes with the word SOME I need to know how many chores she makes.
Step-by-step explanation:
A bag contains 4 red marbles, 11 blue marbles, and 10 yellow marbles. What percent of the marbles are red?
Answers
Answer:
16%
Step-by-step explanation:
4 + 11 + 10 = 25
There are 4 red marbles.
4/25 or 0.16
Find the percentage.
0.16 * 100% = 16%
Best of Luck!
Simplify the expressions:
−8y³ x 5y8
Answers
I hope this helps.
Hi! Your answer is 11. When multiplying terms with exponents, the exponents add up.
Step-by-step explanation:
You want to multiply the terms with the exponents. You should get 3 and 8, add those up and you will get 11.
Hope this helps! Have a good day :)
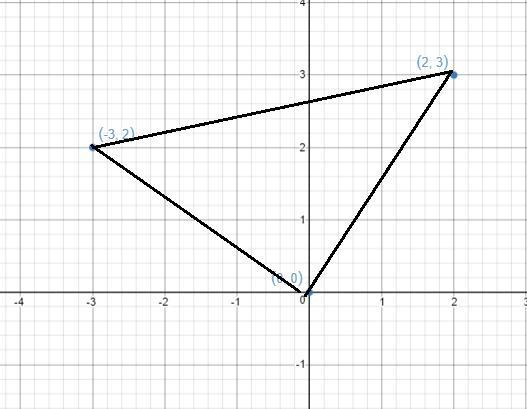
Graph the following points on the coordinate plane. Find the measure of ∠ACB
to the nearest tenth.
A (-3, 2), B (0, 0), C (2, 3)
Answers
The measure of angle ∠ACB is 45 degrees
How to find the measure of ∠ACBFrom the question, we have the following parameters that can be used in our computation:
A (-3, 2), B (0, 0), C (2, 3)
The graph is attached
The lines AB and BC are perpendicular lines
This means that
∠B = 90 degrees
Calculate the length AB and BC using
distance = √[(x2 - x1)² + (y2 - y1)²]
So, we have
AB = √[(-3 - 0)² + (2 - 0)²] = √13
BC = √[(0 - 2)² + (0 - 3)²] = √13
The angle C is then calculated as
tan(C) = AB/BC
tan(C) = √13/√13
tan(C) = 1
Take the arctan of both sides
C = 45
Hence, the measure of ∠ACB is 45 degrees
Read more about angles at
https://brainly.com/question/28293784
#SPJ1
Jean works for the government and was conducting a survey to determine the income levels of a number of different neighborhoods in a metropolitan area. Based on national data, Jean knows that the mean income level in the country is $40,000, with a standard deviation of $2,000. Jean selected three neighborhoods and determined the average income level. What is the probability that the average income level in the neighborhoods was less than $38,000
Answers
Answer:
0.0418 = 4.18% probability that the average income level in the neighborhoods was less than $38,000.
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Jean knows that the mean income level in the country is $40,000, with a standard deviation of $2,000.
This means that \(\mu = 40000, \sigma = 2000\)
Jean selected three neighborhoods and determined the average income level.
This means that \(n = 3, s = \frac{2000}{\sqrt{3}} = 1154.7\)
What is the probability that the average income level in the neighborhoods was less than $38,000
This is the pvalue of Z when X = 38000. So
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{38000 - 40000}{1154.7}\)
\(Z = -1.73\)
\(Z = -1.73\) has a pvalue of 0.0418
0.0418 = 4.18% probability that the average income level in the neighborhoods was less than $38,000.
2) Why is it that when you fill the venn diagram with the number of elements, you
always need to start from the intersection of all sets?
Answers
Answer:
This is because it is easier this way.
You avoid the problem of putting an element in one set and then realizing that the element also belongs to another set, then you must erase something in order to put the element in both sets. Starting with the intersection allows you to know where will be each set in the diagram, and in this way, the diagram should end up being more readable or "clean".
This may seem small, but being "clean" when doing math, will allow you to have an easier time dealing with a lot of problems. And also will be easier for other people when reading your equations and such.
Cliff takes out a $5,000 personal loan with 7
fixed annual interest compounded monthly to pay for his wedding. He repays the loan in 2 year.s
How much total interest does Cliff pay on his loan?
Answers
Cliff pays a total interest of approximately $679.90 on his $5,000 loan.
To calculate the total interest paid on the loan, we need to use the formula for compound interest:
\(A = P(1 + r/n)^{(nt)}\)
Where:
A is the final amount (loan amount + interest)
P is the principal (loan amount)
r is the annual interest rate (in decimal form)
n is the number of times interest is compounded per year
t is the number of years
Given that Cliff takes out a $5,000 loan with a fixed annual interest rate of 7% compounded monthly, we can substitute the values into the formula:
P = $5,000
r = 7% = 0.07
n = 12 (monthly compounding)
t = 2 years
\(A = 5000(1 + 0.07/12)^{(12 \times 2)\)
Calculating this expression:
A ≈ 5000\((1.00583)^{(24)\)
A ≈ 5000(1.13598)
A ≈ 5679.90
The final amount (A) is the loan amount plus the total interest paid. Therefore, to find the total interest paid, we subtract the principal (P) from the final amount (A):
Total Interest = A - P
Total Interest = 5679.90 - 5000
Total Interest ≈ $679.90
For similar question on total interest.
https://brainly.com/question/29415701
#SPJ8
PLEASE HELP WITH THIS ONE QUESTION

Answers
Describe the transformation of LM to L'M'.
10-8
10%
8
6 M
2
6
-8
M
4 6 8 10
OA. LM is translated 5 units left and 2 units up to L'M'.
O B. LM is translated 5 units right and 2 units down to L'M'.
OC. LM is reflected over the x-axis to L'M
O'D. LM is reflected over the yaxis to L'M'.

Answers
Applying a translation of 5 units left and 2 units up to LM yields the transformed figure L'M' and choice A.
What does the graph's rendering look like?A graph can be moved either laterally or vertically parallel to the -axis, and this movement is called a translation.
LM can be converted to L'M' by carefully following the steps below:
The coordinates (10, -8) are translated 5 units left and 2 units up, which means that the location is obtained by deducting 5 from the x-coordinate and adding 2 to the y-coordinate. (5, -6).
Due to its location on the y-axis, the point (10%, 8) does not shift.
The translation of the point (8, 6M) is 5 units left and 2 units up, which indicates Consequently, we need to add 2 to the y-coordinate and remove 5 from the x-coordinate to get the point. (3, 8M).
The coordinates of the point (2, 6) are moved 5 units to the left and 2 units to the up, giving us the coordinates of the point. (-3, 8).
The translation of the point (6, -8) is 5 units left and 2 units up, so we deduct 5 from the x-coordinate and add 2 to the y-coordinate to get the point. (1, -6).
The point (-8, M) is translated 5 units to the left and 2 units to the right, so we take 5 off the x-coordinate and add 2 to the y-coordinate to get the point. (-13, M).
The key argument (4, 6) is translated as 5 units to the left and 2 units to the up, which means we take 5 away from the x-coordinate and add 2 to the y-coordinate to get the location. (-1, 8).
The coordinates (6, 8) are moved 5 units left and 2 units up, which means we need to deduct 5 from the x-coordinate and add 2 to the y-coordinate to get the new coordinates. (1, 10).
As a consequence, option A is produced by applying a translation of 5 units to the left and 2 units to the up to LM, yielding the transformed figure L'M'.
learn more about translation here:
https://brainly.com/question/12463306
#SPJ1
1
What is the y-intercept of a line that has a slope of 4 and passes through point (8, 3)?
3
Ο Ο Ο Ο
11

Answers
Answer:
The slope-intercept form: y = mx + b
m - a slope
b - y-intercept
We have a slope m = 1/4. Substitute: y = 1/4 x + b
We know, the line passes through point (8, 3) → x = 8, y = 3.
Put the values of x and y to the equation of the line:
1/4 · 8 + b = 3
2 + b = 3 |-2
b = 1
Answer: y-intercept is (0, 1)
Step-by-step explanation: