Answers
The sum of infinite geometric series is 25
Explanation:Given:
\(13)\text{ }Geometric\text{ series: }20,\text{ 4, 4/5, . . .}\)To find:
the sum of the infinite series if it diverges
An infinite series converger if -1 < r < 1
We need to check if the value of r values in the above interval
\(\begin{gathered} common\text{ ratio = }\frac{next\text{ term}}{previous\text{ term}} \\ \\ common\text{ ratio = }\frac{4}{20}\text{ = 1/5} \\ \\ common\text{ ratio = }\frac{\frac{4}{5}}{4}\text{ = 1/5} \\ \\ \frac{1}{5}>\text{ -1 but less than 1 \lparen it falls in the interval\rparen} \\ Hence,\text{ it converges} \end{gathered}\)The sum of geometric infinite series is given as:
\(\begin{gathered} S_{\infty}\text{ = }\frac{a}{1-r} \\ \\ a\text{ = 1st term = 20} \\ r\text{ = 1/5} \\ \\ S_{\infty}\text{ = }\frac{20}{1-\frac{1}{5}} \end{gathered}\)\(\begin{gathered} S_{\infty}\text{ = }\frac{20}{\frac{5-1}{5}}\text{ = }\frac{20}{\frac{4}{5}} \\ \\ S_{\infty}\text{ = 20 }\div\frac{4}{5} \\ \\ S_{\infty}\text{ = 20 }\times\frac{5}{4} \\ \\ S_{\infty}\text{ = 25} \end{gathered}\)Related Questions
On each trial of an experiment, a participant is presented with a constant soft noise, which is interrupted at some unpredictable time by a slightly louder sound. The time it takes for the participant to react to the louder sound is recorded. The following list contains the reaction times (in milliseconds) for 8 trials of this experiment:
486, 358, 395, 759,496, 692, 353, 306 0
(a) What is the mean of this data set? If your answer is not an integer, round your answer to one decimal place.
(b) What is the median of this data set? If your answer is not an integer, round your answer to one decimal place.
(c) How many modes does the data set have, and what are their values?
Answers
Answer:
480.6 ; 440.5, 8 mode values
Step-by-step explanation:
Given that :
Given the data :
486, 358, 395, 759,496, 692, 353, 306
Rearranged data: 306, 353, 358, 395, 486, 496, 692, 759
The mean:
Σx/ n
n = sample size = 8
Σx = sum of all data values = 3845
Mean = 3845 / 8
Mean = 480.6
The median :
0.5(n + 1)th term
0.5(8 + 1) th term
0.5(9)th term
= 4.5term
(4th + 5th term) / 2
(395 + 486) / 2
= 440.5
The mode = most frequently occurring data value ; since all the data values have a frequency of 1, then the number of modes = 8.
Find the volume of the cubes or rectangular prisms in cubic centimeters.
Answers
Answer:1st cube 2nd box 2nd cube 3rd box 4th cube 1st box and 1st cube 1st box
Step-by-step explanation:
The asked volumes are 36/125 cm³, 6/125 cm³, 1/125 cm³ and 8/125 cm³
What is volume?Volume is defined as the space occupied within the boundaries of an object in three-dimensional space.
Given are dimensions of cuboid and cubes, we are asked to find their volumes.
We know that, volume of cube = side³
Volume of cuboid = length · width · height
1) Dimensions of the cuboid = 3/5, 4/5, 3/5
Volume = 3/5×3/5×4/5 = 36/125 cm³
2) Dimensions of the cuboid = 1/5, 2/5, 3/5
Volume = 1/5×2/5×3/5 = 6/125 cm³
3) Side of the cube = 1/5 cm
Volume = (1/5)³ = 1/125 cm³
4) Side of the cube = 2/5 cm
Volume = (2/5)³ = 8/125 cm³
Hence, the asked volumes are 36/125 cm³, 6/125 cm³, 1/125 cm³ and 8/125 cm³
For more references on volume, click;
https://brainly.com/question/28058531
#SPJ2
what is the solution to the equation:
5(n - 1/10) = 1/2
a. n= 13/5
b. n= 3/25
c. n= 0
d. n= 1/5
Answers
\( \sf \longrightarrow \: 5 \bigg( \: n - \frac{1}{10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: 5 \bigg( \: \frac{n}{1} - \frac{1}{10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: 5 \bigg( \: \frac{10 \times n - 1 \times 1}{1 \times 10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: 5 \bigg( \: \frac{10n - 1}{ 10} \bigg) = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: \: \frac{50n - 5}{ 10} = \frac{1}{2} \\ \)
\( \sf \longrightarrow \: \: 2(50n - 5) =1(10) \\ \)
\( \sf \longrightarrow \: \: 2(50n - 5) =10 \\ \)
\( \sf \longrightarrow \: \: 100n - 10=10 \\ \)
\( \sf \longrightarrow \: \: 100n =10 + 10\\ \)
\( \sf \longrightarrow \: \: 100n =20\\ \)
\( \sf \longrightarrow \: \:n = \frac{2 \cancel{0}}{10 \cancel{0}} \\ \)
\( \sf \longrightarrow \: \:n = \frac{1}{5} \\ \)
Answer:-
Answer:- D) n = ⅕ ✅To solve the equation \(\sf 5(n - \frac{1}{10}) = \frac{1}{2} \\\) for \(\sf n \\\), we can follow these steps:
Step 1: Distribute the 5 on the left side:
\(\sf 5n - \frac{1}{2} = \frac{1}{2} \\\)
Step 2: Add \(\sf \frac{1}{2} \\\) to both sides of the equation:
\(\sf 5n = \frac{1}{2} + \frac{1}{2} \\\)
\(\sf 5n = 1 \\\)
Step 3: Divide both sides of the equation by 5 to isolate \(\sf n \\\):
\(\sf \frac{5n}{5} = \frac{1}{5} \\\)
\(\sf n = \frac{1}{5} \\\)
Therefore, the solution to the equation \(\sf 5(n - \frac{1}{10})\ = \frac{1}{2} \\\) is \(\sf n = \frac{1}{5} \\\), which corresponds to option (d).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
A car travels a distance of 112km at an average Speed of 70km/h. It then Travells Further for 60km at an average Speed of 50 km/hr. Calculate for the entire Journey of the total time taken.
Answers
The total time taken for the entire journey is 2.8 hours.
To calculate the total time taken for the entire journey, we can use the formula:
Time = Distance / Speed
For the first part of the journey, the car travels a distance of 112 km at an average speed of 70 km/h. Using the formula, the time taken for this part is:
Time1 = 112 km / 70 km/h = 1.6 hours
For the second part of the journey, the car travels a further distance of 60 km at an average speed of 50 km/h. Again, using the formula, the time taken for this part is:
Time2 = 60 km / 50 km/h = 1.2 hours
To find the total time for the entire journey, we sum up the times for both parts:
Total Time = Time1 + Time2 = 1.6 hours + 1.2 hours = 2.8 hours
For more such questions on time
https://brainly.com/question/26862717
#SPJ8
Pls make the answer clear & gave an easy explanation thank u
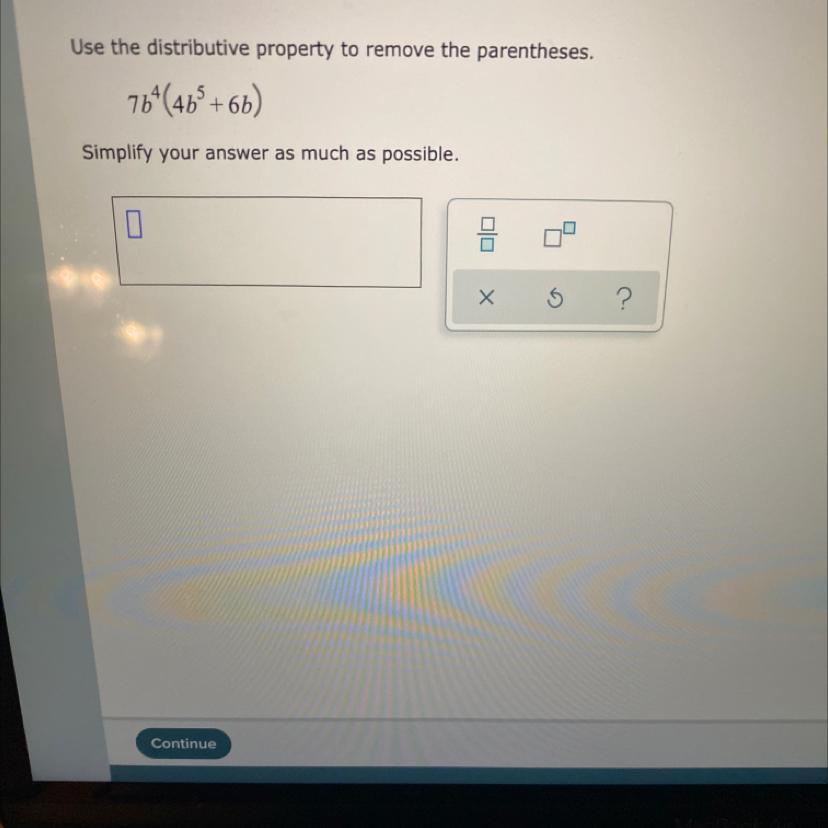
Answers
Given 3 numbers a, b and c the distributive property states that:
\(a\cdot(b+c)=a\cdot b+a\cdot c\)If we apply this property to the expression given by the question we get:
\(7b^4\cdot(4b^5+6b)=7b^4\cdot4b^5+7b^4\cdot6b\)It's important to recall the following property of powers:
\(b^a\cdot b^c=b^{a+c}\)Using this we can simplify the last expression:
\(\begin{gathered} 7b^4\cdot4b^5+7b^4\cdot6b=7\cdot4\cdot b^{4+5}+7\cdot6\cdot b^{4+1} \\ 7b^4\cdot4b^5+7b^4\cdot6b=28b^9+42b^5 \end{gathered}\)Then the answer is:
\(28b^9+42b^5\)2) Ayanda wants to invest R200 000. The bank offers him 2 options for his
6 year investment.
Option 1: 12% Simple interest p.a.
Option 2: 9,5% Compound interest p.a.
4.2.1) Calculate the return on Ayanda's investment using Option 1.
●
●
4.2.2) Calculate the return on Ayanda's investment using Option 2.
4.2.3) Which option will render the most money?
Answers
Answer:
4.2.1) R140 000
4.2.2) R144 758.28
4.2.3) Option 2
Step-by-step explanation:
To calculate the return on Ayanda's investment using Option 1, we can use the simple interest formula.
\(\boxed{\begin{minipage}{7 cm}\underline{Simple Interest Formula}\\\\$ I =Prt$\\\\where:\\\\ \phantom{ww}$\bullet$ $I =$ interest accrued \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}\)
Given values:
P = R200 000r = 12% = 0.12t = 6 yearsSubstitute the given values into the formula and solve for I:
\(I=200000 \cdot 0.12 \cdot 6\)
\(I=24000 \cdot 6\)
\(I=144000\)
Therefore, the return on Ayanda's investment using Option 1 is R144000.
\(\hrulefill\)
To calculate the return on Ayanda's investment using Option 2, we can use the compound interest formula.
\(\boxed{\begin{minipage}{7 cm}\underline{Annual Compound Interest Formula}\\\\$ I=P\left(1+r\right)^{t}-P$\\\\where:\\\\ \phantom{ww}$\bullet$ $I =$ interest accrued \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}\)
Given values:
P = R200 000r = 9.5% = 0.095t = 6 yearsSubstitute the given values into the formula and solve for I:
\(I=200000(1+0.095)^6-200000\)
\(I=200000(1.095)^6-200000\)
\(I=200000(1.72379142...)-200000\)
\(I=344758.28426...-200000\)
\(I=144758.28426...\)
\(I=144758.28\)
Therefore, the return on Ayanda's investment using Option 2 is R144758.28.
\(\hrulefill\)
Comparing the returns from both options, we find that Option 1 offers a return of R144000, while Option 2 offers a return of R144758.28. As R144758.28 > R144000, then Option 2 will render the most money for Ayanda's investment.
Lin surveyed a class of sixth-graders asking how many hours they spend online every month.
Answers
They spend about three hours a day online
1/10 (x + 11) = -2 (8 - x)
Answers
Answer: (5/8)x
Step-by-step explanation:
multiply both side by 10
x + 11 = -20 (8-x)
x + 11 = -160 + 20x
11 + 160 = 20x-x
171 = 19x
x =9
What are the coordinates of the original point, G?
Answers
The answer is (-4,3)
The reason is because you move -4 steps to the left. and 3 steps upward to get to G.
Mark me Brainliest. :)
Find the unknown length x in the right triangle, to the nearest tenth.
R
11
250
Answers
X=26.0282
9) Angeline bought s yards of satin fabric priced ot $8.09 per yard, ond c
yards of cotton fabric priced at $3.79 per yard. Which of the following is on
expression that can be used to determine the amount of money that
Angeline would spend in all on fabric? *
2 points
O 8.09s - 3.79c
O 8.09c +3.79s
8,09c 3.79s
O 8.09s +3.79c
Answers
Answer:
8.09s + 3.79c
Step-by-step explanation:
The $8.09 is pertaining to the satin (s) and the $3.79 is pertaining to the cotton fabric (c).
Answer:
70.77
Step-by-step explanation:
Hope this helps
how to solve this question
Answers
For the trigonometric identity
11. If cos 27° = x, then the value of tan 63° interims of "x" is x/√1 - x²
12. If Θ be an acute angle and 7sin²Θ + 3 cos²Θ= 4, then tan Θ is 1/√3
13. The value of tan 80° × tan 10° + sin² 70° + sin² 20° is 2
14. The value of (sin 47°/cos 43°)² + (cos 43°/sin 47°) - 4 cos²45° is 0
15. If 2 (cos²Θ - sin²Θ) = 1, Θ is a positive acute angle them the value of Θ is 30°
16. If 5 tan Θ = 4, then (5 sin Θ - 3 cos Θ)/(5 sin Θ + 2 cos Θ) is equal to 1/6
17. If sin(x + 20)° = cos (x + 10)° then the value of "x" is 30°
18. The value of (sin 65°)/ (cos 25°) is 1
How do we find the various trigonometric identity?To solve the various trigonometric identity;
11. Given: cos 27° = x
We know that cos (90 - θ) = sin θ
So, cos 63° = sin 27°
And sin 63° = √1 - cos²27°
Substituting cos 27° = x, we get
sin 63° = √1 - x²
Therefore, Therefore, tan 63° = sin 63° / cos 63° = cos 27° / cos 63° = x / cos 63°.
= x/√1 - x²
12. Given: Θ is an acute angle and 7sin²Θ + 3 cos²Θ= 4
Since Θ is an acute angle, sin²Θ + cos²Θ = 1
Substituting sin²Θ + cos²Θ = 1 into the equation 7sin²Θ + 3 cos²Θ= 4, we get
7 (sin²Θ/ cos²Θ) + 3 = 4/cos²Θ - 4 sec²Θ
⇒ 7tan²Θ + 3 = 4(1 + tan²Θ)
⇒ 7tan²Θ + 3 = 4 + 4 tan²Θ
⇒3 tan²Θ = 1
⇒ tan²Θ = 1/3
⇒ tanΘ = 1/√3
13. For tan 80° × tan 10° + sin² 70° + sin² 20°
⇒ tan 80° = cot (90 - 80)° = cot 10°
⇒ sin 70° = cos (90 - 70) = cos 20°
⇒ cot 10° × tan 10° + cos 20° + sin² 20°
= 1 + 1 = 2
14. (sin 47°/cos 43°)² + (cos 43°/sin 47°) - 4 cos²45°
= (sin 47°/cos43°)² + (cos 43°/sin 47°)² - 4(1/√2)²
= (sin (90° - 43°)/cos43°)² + (cos (90° - 47°)/sin)² = 4(1/2)
= (cos 43°/cos 43°)² + (sin 47°/ sin 47°)² - 2
= 1 + 1 - 2 = 0
15. 2 (cos²Θ - sin²Θ) = 1
cos²Θ - sin²Θ = 1/2
Since Θ is an acute angle, sin²Θ + cos²Θ = 1
Substituting sin²Θ + cos²Θ = 1 into the equation cos²Θ - sin²Θ = 1/2, we get
cos²Θ - (1 - cos²Θ) = 1/2
2cos²Θ = 3/2
cos Θ = √3/2(cos 30° = (√3)/2
= 30°
16. Given: 5 tan Θ = 4
We know that tan Θ = sin Θ / cos Θ
So, 5 sin Θ / cos Θ = 4
5 sin Θ = 4 cos Θ
Dividing both sides of the equation by 5, we get
sin Θ / cos Θ = 4/5
∴ sin Θ = 4/5 cos Θ
given that the expression is (5 sin Θ - 3 cos Θ)/(5 sin Θ + 2 cos Θ)
we substitute sin Θ = 4/5 cos Θ into the equation
⇒(5 × 4/5 cos Θ - 3 cos Θ)/(5 × 4/5 cos Θ + 2 cos Θ)
= (4-3)/(4 + 2) = 1/6
17. Given: sin(x + 20)° = cos (x + 10)°
We know that sin(90 - θ) = cos θ
So, sin(x - 20)° = sin(90 - (3x + 10))°
⇒ (x - 20)° = (90 - (3x + 10))°
⇒ x - 20° = 90° - 3x + 10
⇒ 4 x = 120°
⇒ x = 120°/4
⇒ x = 30°
18. To find the value of (sin 65°) / (cos 25°), we can use the trigonometric identity:
To solve this, we can use the following trigonometric identities:
sin(90 - θ) = cos θ
cos(90 - θ) = sin θ
We can also use the fact that sin²θ + cos²θ = 1.
Rewrite sin (65°) / cos (25°)
⇒ sin (65°) = cos (25°)
∴ cos (25°)/ cos (25°) = 1
Find more exercises on trigonometric identity;
https://brainly.com/question/24377281
#SPJ1
0.9t
t² + 64
Find the time
The concentration of a drug t hours after being injected is given by C(t) =
when the concentration is at a maximum. Give your answer accurate to at least 2 decimal places.
hours.
Calculator
Submit Question
Answers
On a residential single lane road there was a wreck that backed up traffic for 5 miles. 80% of the traffic consists of cars and 20% of the traffic consists of trucks. The average distance between vehicles is 3 feet. The average length of a car is 13.5 feet and the average length of a truck is 20 feet. Estimate how many vehicles are stuck in the traffic jam. (Hint: There are 5280 feet in 1 mile.) A. 853 vehicles B. 1510 vehicles C. 2103 vehicles D. 2320 vehicles
Answers
Answer: b) 1510 vehicles
Step-by-step explanation:
Total: 5 miles x 5280 ft per mile = 26,400
Cars: 80% of vehicles are cars with a length of 13.5 = 0.8(13.5)v = 10.8v
Trucks: 20% of vehicles are trucks with length of 20 = 0.2(20)v = 4v
Between: Distance between two vehicles is 3: (3/2)v = 1.5v
Total = Cars + Trucks + Between
26,400 = 10.8v + 4v + 1.5v
26,400 = 16.3v
1619.6 = v
the closest number of all of the options is (b) 1510
HELP ILL GIVE YOU EXTRA POINTS question up top
Answers
Answer:
I think the answer is x^2
Answer: x^2+4
Step-by-step explanation:
It would be more than the other numbers with exponents since it has a plus 2.
18=a ÷ 12
Find the introvert
Answers
Answer:
a = 216
Step-by-step explanation:
A = {5, 6, 7, 8, 9, 10} and B = {2, 3, 4, 5, 11, 12, 13}. What is A∪B? What is A∩B?
Answers
Step-by-step explanation:
A U B= {2,3,4,5,6,7,8,9,10,11,12,13}
A n B= {5}
A couple plans to purchase a house. The bank requires a 20% down payment on the $240,000 house. The couple will finance the rest of the cost with a fixed- rate mortgage at 8.5% annual interest with monthly payments over 30 years.
Complete the parts below. Do not round any intermediate computations. Round your final answers to the nearest cent if necessary. If necessary, refer to the list of financial formulas.
(a) Find the required down payment.
(b) Find the amount of the mortgage.
(c) Find the monthly payment.
Answers
(A) The required down payment is $48,000.
(B) The amount of the mortgage is $192,000.
(C) Monthly payment = $192,000 * (0.085/12) * (1 + (0.085/12))^(3012) / (((1 + (0.085/12))^(3012)) - 1)
(a) To find the required down payment, we need to calculate 20% of the house price.
Down payment = 20% of $240,000
Down payment = 0.2 * $240,000
Down payment = $48,000
The required down payment is $48,000.
(b) The amount of the mortgage is equal to the total cost of the house minus the down payment.
Mortgage amount = Total cost of the house - Down payment
Mortgage amount = $240,000 - $48,000
Mortgage amount = $192,000
The amount of the mortgage is $192,000.
(c) To find the monthly payment for the mortgage, we can use the formula for the monthly payment on a fixed-rate mortgage:
Monthly payment = P * r * (1 + r)^n / ((1 + r)^n - 1)
Where:
P = Principal amount (mortgage amount)
r = Monthly interest rate (8.5% annual interest divided by 12 months and converted to a decimal)
n = Total number of monthly payments (30 years multiplied by 12 months)
Monthly payment = $192,000 * (0.085/12) * (1 + (0.085/12))^(3012) / (((1 + (0.085/12))^(3012)) - 1)
Using this formula and performing the calculation will give you the monthly payment amount.
for more questions on down payment
https://brainly.com/question/1698287
#SPJ8
Eight less than four times a number is less than 56. What are the possible values of that number?
X> 12
x < 12
ООО
x < 16
O x> 16
Answers
Answer:
x < 16
Step-by-step explanation:
Let the number be x
Four time the number = 4x
Eight less than four times the number = 4x - 8
Eight less than four times the number is less than 56,
that is , 4x - 8 < 56
4x - 8 + 8 < 56 + 8 [ adding both sides by 8 ]
4x + 0 < 64
4x < 64 [ divide both sides by 4 ]
x < 16
A magazine costs 4.95 per month. If you buy a one year subscription, it's 30% cheaper. How much will you pay in one year with the discount?
Answers
Answer:
41.48/year
Step-by-step explanation:
4.95 x 12 = 59.40
59.40 × .30 = 17.82
59.40 - 17.82 = 41.48
1. If the discriminant of a quadratic equation is zero, what do you know about the type and number of roots of the quadratic equation?
A. The quadratic equation has one real number root.
B. The quadratic equation has one imaginary and one real number root.
C. The quadratic equation has two imaginary number roots.
D. The quadratic equation has two distinct real number roots.
Answers
Answer:
C
Step-by-step explanation:
Using the concept of the discriminant of a quadratic equation, the correct option is:
A. The quadratic equation has one real number root.
--------------------------
A quadratic equation is given by:
\(y = ax^2 + bx + c\)
The discriminant is:
\(\Delta = b^2 - 4ac\)
If the discriminant is positive, that is, \(\mathbf{\Delta > 0}\), the equation has two distinct real roots.If the discriminant is zero, that is, \(\mathbf{\Delta = 0}\), the equation has two equal real roots, which is also considered one real root.If the discriminant is negative, that is, \(\mathbf{\Delta < 0}\), the square root of a negative number will be calculated, and thus, the equation has two imaginary number roots.In this question, \(\Delta = 0\), thus, one real root, option A.A similar problem is given at https://brainly.com/question/2288755
Find the length of AC
A. 377.19
B. 378.63
C. 2.89
D. 33.13
Answers
Answer:
AC = 377.19
Step-by-step explanation:
Since this is a right triangle, we can use trig functions
tan theta = opp /adj
tan 5 = 33/AC
AC tan 5 = 33
AC = 33/ tan 5
AC = 377.19
What is 450,000,000 written in scientific
notation?
Answers
Amount Desired at End of Period $ 17,600.00 Length of time 7 Rate 2% Compunded Quartly Required:
Complete the following using the information above and the present value Table 12.3 or the present value table in the Business Math Handbook or the present value formula to answer the following:
Note: Use cells A2 to D3 from the given information to complete this question.
1. Period Used
2. Rate Used
3. PV factor used
4. PV of amount desired at end of period
Answers
Using the given information to complete this compounding interest question is as follows:
1. Period Used = 28 quarters
2. Rate Used = 2%
3. PV factor used = 1.14987
4. PV of the amount desired at end of the period = $15,306.04.
What is compound interest?Compound interest adds the accumulated interest to the principal amount after each period in order to compute the period's interest.
Compound interest is the opposite of simple interest, which does not add the accumulated interest to the principal before computing another period's interest.
N (# of periods) = 28 quarters (7 x 4)
I/Y (Interest per year) = 2%
PMT (Periodic Payment) = $0
FV (Future Value) = $17,600
Results:
PV = $15,306.04
Total Interest = $2,293.96
PV factor = 1.14987
Learn more about compound interest at brainly.com/question/24274034
#SPJ1
The distance y (in miles) that a car travels on a highway in x minutes is represented by the equation y=1.1x. The graph shows the distance that a bus travels. Find the speed of each vehicle. Which vehicle is traveling faster?
Answers
Answer:
car = 1.1 mi/min
bus = 1.05 mi/min
car travels faster
Step-by-step explanation:
recall that speed is given by the gradient (i.e slope) of a distance vs time graph or equation.
for the car:
equation is y = 1.1x
recall that for an equation in the form y = mx + b, slope = m
if we compare the given equation to the general equation, it is clear that
speed of car = slope = m = 1.1 miles/min (answer)
for the bus,
we are given 2 points (2,2.1) and (4,4.2)
if we apply the formula for slope (see attached for reference)
slope, m
= (4.2 - 2.1) / (4 - 2)
= 2.1 / 2
= 1.05 mi/min= speed of bus (answer)
comparing the 2 speeds, we can see that the car has the higher speed (travels faster).
Answer:
Car:1.1
Bus:1.05
Car is going faster.
Step-by-step explanation:
This is right. I got it right on Big Ideas Math (Pre-Algebra)
What is the sequence equation 8, 17, 35, 71, 143
Answers
Answer:
Step-by-step explanation:
What you do is multiply the previous number and add 1 to get the next answer.
Equation An = 2(An-1)+1
n = The Term
Mr. Olsen has a computer business in which he sells everything at 44.5% above the wholesale price. If he purchased a printer for $80 wholesale, what will be the retail price?
Answers
If he purchased a printer for $80 wholesale. Then the retail price will be $115.60.
What is the percentage?The amount of any product is given as though it was a proportion of a hundred. The ratio can be expressed as a quarter of 100. The phrase % translates to one hundred percent. It is symbolized by the character '%'.
The percentage is given as,
Percentage (P) = [Final value - Initial value] / Initial value x 100
Mr. Olsen has a PC business wherein he sells everything at 44.5% above the wholesale price. On the off chance that he bought a printer for $80 wholesale.
Then the retail price is given as,
⇒ $80 x (1 + 0.445)
⇒ $80 x 1.445
⇒ $115.60
If he purchased a printer for $80 wholesale. Then the retail price will be $115.60.
More about the percentage link is given below.
https://brainly.com/question/8011401
#SPJ1
A rental car company charges a fee of $150.00 for renting a car for a week plus $0.25 per mile driven.
Answers
Answer:
y = 150z + .25x
y = $ amount of rental
z = weeks rented
x = miles driven
i hope this helps :)
−76 times the difference between a number and 61 is equal to the number plus −89.
Answers
Two or more expressions with an equal sign is Equation.-76(x-61)=x-89 is the equation for −76 times the difference between a number and 61 is equal to the number plus −89.
What is Equation?Two or more expressions with an equal sign is called as Equation.
The sentence −76 times the difference between a number and 61 is equal to the number plus −89. We have to express in the form of equation.
−76 times the difference between a number
Let the number be 'x', times means multiplication and difference is subtraction.
-76(x-61)
the number plus −89
x+(-89)
−76 times the difference between a number and 61 is equal to the number plus −89.
-76(x-61)=x+(-89)
-76(x-61)=x-89
Therefore -76(x-61)=x-89 is the required equation.
To learn more on Equation click:
https://brainly.com/question/21105092
#SPJ1
Amadi is three times as old as Chima. The sum of their ages is 24
Answers
Answer:
Amadi: 20 years old
Chima : 4 years old