Quadrilateral a has side lengths 2,3,5 and 6. quadrilateral b has single length 4,5,8 and 10 could one of the quadrilateral be a scale copy of the other
Answers
Quadrilateral b, is not a scaled copy of Quadrilateral a.
The side length of Quadrilateral a=2,3,5, and 6.
The side length of Quadrilateral b=4,5,8 and 10
Now comparing the Ratio of the Corresponding Sides of two quadrilaterals a and b
2/4 ≠ 5/8
3/5 ≠ 6/10
Since the ratio of corresponding opposite sides is not equal. The two Quadrilateral are Not Similar.
So, We can say that Quadrilateral b, is not a scaled copy of Quadrilateral a.
For more information on quadrilaterals click on the link below:
https://brainly.com/question/23935806
#SPJ4
Related Questions
In an experimental study, random error due to individual differences can be reduced if a(n) _____ is implemented.
Answers
In an experimental study, random error due to individual differences can be reduced if a(n) control group is implemented.
One effective way to reduce random error due to individual differences in an experimental study is to include a control group. A control group serves as a baseline comparison group that does not receive the experimental treatment. By having a control group, researchers can isolate and measure the effects of the independent variable more accurately.
The control group provides a point of reference to assess the impact of individual differences on the study's outcome. Since both the experimental group and control group are subject to the same conditions, any observed differences can be attributed to the experimental treatment rather than individual variations.
This helps to minimize the influence of confounding variables and random error associated with individual differences.
By comparing the outcomes of the experimental group and control group, researchers can gain insights into the specific effects of the treatment while controlling for individual differences. This improves the internal validity of the study by reducing the potential bias introduced by individual variability.
In summary, including a control group in an experimental study helps to reduce random error due to individual differences by providing a comparison group that is not exposed to the experimental treatment. This allows researchers to isolate and measure the effects of the independent variable more accurately.
Learn more about Implemented
https://brainly.com/question/32093242
https://brainly.com/question/32181414
#SPJ11
Find the product of 64 and 12.
Answers
Answer:
768
Step-by-step explanation:
64 x 12 = 768
Answer:
768
Step-by-step explanation:
What is the equation for the line parallel to y=2x+13y=2x+13 that contains (8,-4)(8,−4)?
Answers
I will assume you meant y = 2x + 13
Answer: y = 2x - 20
Suppose a system of equations was solved my elimination and the resulting equation was 0=3. Which of the following statements is/are true.
a. The slopes of the two equations in the system are the same but their y-intercepts are different.
b. The system is an independent system.
c. The graphs of the two equations would intersect at the point (0,3).
Answers
Answer:
a. The slopes of the two equations in the system are the same but their y-intercepts are different.Step-by-step explanation:
The system resulting in equation 0=3 means:
There is no solutionThe lines are parallel as no intersectionCorrect choice is:
a. The slopes of the two equations in the system are the same but their y-intercepts are different.find an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is 5xy. (note: start your answer with y
Answers
The equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is y = (5/2) * x^2y + 1. This equation represents a curve where the y-coordinate is a function of the x-coordinate, satisfying the conditions.
To determine an equation of the curve that satisfies the conditions, we can integrate the slope function with respect to x to obtain the equation of the curve. Let's proceed with the calculations:
We have:
Point: (0, 1)
Slope: 5xy
We can start by integrating the slope function to find the equation of the curve:
∫(dy/dx) dx = ∫(5xy) dx
Integrating both sides:
∫dy = ∫(5xy) dx
Integrating with respect to y on the left side gives us:
y = ∫(5xy) dx
To solve this integral, we treat y as a constant and integrate with respect to x:
y = 5∫(xy) dx
Using the power rule of integration, where the integral of x^n dx is (1/(n+1)) * x^(n+1), we integrate x with respect to x and get:
y = 5 * (1/2) * x^2y + C
Applying the initial condition (0, 1), we substitute x = 0 and y = 1 into the equation to find the value of the constant C:
1 = 5 * (1/2) * (0)^2 * 1 + C
1 = C
Therefore, the equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is:
y = 5 * (1/2) * x^2y + 1
Simplifying further, we have:
y = (5/2) * x^2y + 1
To know more about equation of the curve refer here:
https://brainly.com/question/31467851#
#SPJ11
I WILL MARK YOU BRAINLIEST IF YOU ANSWER
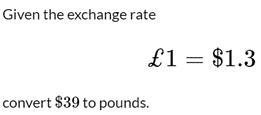
Answers
Answer:
29.25 Pound sterling
Answer:
50.7? I think ..,.
Step-by-step explanation:
39*1.3 = 50.7
"Let f be the function given by f(x) = (x² + x) cos(5x).
What is the average value of f on the closed interval [2, 6]?" A -7.392 B -1.848 С 0.722 D 2.878
Answers
The answer is A.To find the average value of a function f(x) on a closed interval [a,b], we use the formula:
1/(b-a) ∫[a,b] f(x) dx
In this case, we need to find the average value of the function f(x) = (x² + x) cos(5x) on the closed interval [2,6]. So, we plug in the values of a and b:
1/(6-2) ∫[2,6] (x² + x) cos(5x) dx
Simplifying this expression, we get:
1/4 ∫[2,6] (x² + x) cos(5x) dx
Now, we need to evaluate the integral. We can use integration by parts to do this:
u = (x² + x) dv = cos(5x) dx
du/dx = 2x + 1 v = (1/5) sin(5x)
∫(x² + x) cos(5x) dx = (x² + x)(1/5) sin(5x) - ∫(2x + 1)(1/5) sin(5x) dx
= (x² + x)(1/5) sin(5x) - (2/25) cos(5x) - (1/25) x sin(5x) + C
Plugging in the limits of integration, we get:
1/4 [(6² + 6)(1/5) sin(30) - (2/25) cos(30) - (1/25) (6) sin(30) - (2² + 2)(1/5) sin(10) + (2/25) cos(10) + (1/25) (2) sin(10)]
Simplifying this expression, we get:
-7.392
So, the average value of f(x) on the closed interval [2,6] is -7.392. Therefore, the answer is A.
learn more about closed intervals here: brainly.com/question/30191972
#SPJ11
The cone shown below is made from the sector shown.
(a) Find the slant length s cm,
(b) Find the arc length of the sector,
(c) Explain why the slant height s is the same as the radius r of the sector.

Answers
The slant height s is equal to the radius r of the sector.
(a) The Pythagorean theorem must be applied in order to determine the slant length s. We are aware that the cone's height is 12 cm, and that its radius is 8 cm (or half its diameter). The hypotenuse of a right triangle with 8 and 12 cm in length is the slant height (s). We thus have:
s² = r² + h²
s² = 8² + 12²
s² = 64 + 144
s² = 208
s = √208
s ≈ 14.42 cm
(b) The sector's arc length can be calculated using the formula L = (/360) 2r, where is the sector's angle in degrees and r is its radius. In this instance, the sector's radius is 8 cm, and its angle is 120° (as shown in the diagram). We thus have:
L = (120/360) × 2π(8)
L = (1/3) × 16π
L = (16/3)π
L ≈ 16.76 cm
(c) The cone's slant height s is the distance along a slanted line from the apex (top) to the base. The sector's radius, or r, is the distance measured around the sector's circumference from its centre to any other point. Since the sector forms the base of the cone, the sector's radius likewise serves as the base of the cone. According to the Pythagorean theorem, the cone's radius r and slant height s are connected (a).
As a result, the sector's radius r and slant height s are equal.
To know more about Slant height visit:
https://brainly.com/question/26949672
#SPJ1
In the diagram, the measure of angle 8 is 124º, and the measure of angle 2 is 84°

Answers
Answer:
whats the question?
Step-by-step explanation:
Answer:
Angle 7 = 56 °
Step-by-step explanation:
Angles 8 and 7 = 180 degrees
To get the degree of angle 7 subtract 124 from 180
180 - 124 = 56 degrees
Angle 7 = 56 degrees
PLEASE ANSWER IN HANDWRITING AND FORMULAS! SHOW WORK
COMPLETELY! I WILL GIVE THUMBE UP!
4. If you deposit money today in an account that pays 4.5 % annual interest, how long will it take to double your money?
Answers
I apologize, but as a text-based AI model, I am unable to provide handwritten answers or show work in form of formulas. To determine annual interest rate of 4.5%, we can use compound interest formula.
To determine how long it will take to double your money with an annual interest rate of 4.5%, we can use the compound interest formula:
A = P(1 + r/n)^(nt)
Where:
A = Final amount (double the initial amount)
P = Principal (initial amount)
r = Annual interest rate (as a decimal)
n = Number of times interest is compounded per year
t = Time (in years)
In this case, we want to find the value of t. Let's assume the initial amount is P, and the final amount is 2P (double the initial amount). Substituting these values into the formula, we have:
2P = P(1 + 0.045/n)^(nt)
To solve for t, we can divide both sides of the equation by P and simplify:
2 = (1 + 0.045/n)^(nt)
Taking the natural logarithm (ln) of both sides of the equation:
ln(2) = nt ln(1 + 0.045/n)
Now, we can solve for t:
t = ln(2) / (n ln(1 + 0.045/n))
The value of n will depend on how frequently the interest is compounded (e.g., annually, semi-annually, quarterly, etc.). By substituting the appropriate value for n and evaluating the expression, you can determine the time it will take to double your money. Note: If you provide the specific compounding period, I can assist you in calculating the exact time it takes to double your money.
To learn more about compound interest click here : brainly.com/question/14295570
#SPJ11
help plz !! Which is the graph of an even monomial function?
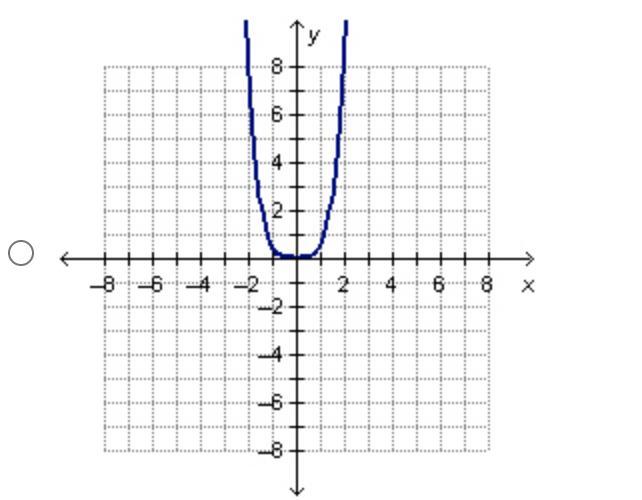



Answers
Answer:
Imagie 1 and 2
monomial function graph look like this
<3 ily
Red

Answer:
The first image
Explanation:
Hope you have a great day!
Giving 50 points for help on this equation please
In the figure below, a line intersects two parallel lines. Find the missing angle measurements and then use the word bank to name the angle relationships

Answers
Answer:
Step-by-step explanation:
to find a:
a is a supplementary angle meaning that it and the 50 add to 180.
therefore
a = 180 - 50
a = 130
to find b:
b and 50 are vertically opposite angles meaning that they are the same
b = 50
to find c:
c and 50 are supplementary angles meaning they add to 180
c = 180 - 50
c = 130
** a and c are also vertically opposite meaning they equal the same
to find e:
b and e are interior angles meaning they add to 180
e = 180 - b
e = 180 - 50
e = 130
to find f:
e and f are supplementary angles meaning they add up to 180
f = 180 - 130
f = 50
to find h:
h and f are vertically opposite angles meaning they are the same
h = 50
the length of a rectangle is 3m less than double the width, and the area of the rectangle is 14 m^2 . find the dimensions of the rectangle.
Answers
The dimensions of the rectangle are width = 7/2 meters and length = 4 meters.
Let's assume that the width of the rectangle is x meters. According to the given information, the length of the rectangle is 3 meters less than double the width, which can be expressed as 2x - 3.
The area of a rectangle is given by the formula: Area = Length × Width. In this case, the area is given as 14 m². Therefore, we can write the equation:
(x)(2x - 3) = 14
Expanding the equation:
2x² - 3x = 14
Rearranging the equation to standard form:
2x² - 3x - 14 = 0
To solve this quadratic equation, we can factor it or use the quadratic formula. In this case, let's use the quadratic formula:
x = (-b ± √(b² - 4ac)) / (2a)
In our equation, a = 2, b = -3, and c = -14. Plugging in these values into the quadratic formula:
x = (-(-3) ± √((-3)² - 4(2)(-14))) / (2(2))
x = (3 ± √(9 + 112)) / 4
x = (3 ± √121) / 4
x = (3 ± 11) / 4
Simplifying further:
x = (3 + 11) / 4 or x = (3 - 11) / 4
x = 14 / 4 or x = -8 / 4
x = 7/2 or x = -2
Since the width cannot be negative, we discard the negative solution. Therefore, the width of the rectangle is 7/2 meters.
Now, we can substitute the value of x into the expression for the length:
Length = 2x - 3
Length = 2(7/2) - 3
Length = 7 - 3
Length = 4 meters
Thus, the dimensions of the rectangle are width = 7/2 meters and length = 4 meters.
for more such question on rectangle visit
https://brainly.com/question/25292087
#SPJ8
Please help!!! I don’t really understand this at all

Answers
- point M is the midpoint of segment AB
9514 1404 393
Answer:
a, b, e (only)
Step-by-step explanation:
The circle centered at A is all of the points that are distance AB from A.
The circle centered at B is all of the points that are distance AB from B.
The points C and D are points that are distance AB from both A and B.
The line joining those points (C and D) consists entirely of points that are equal distances from A and from B. CD is the perpendicular bisector of AB.
Point M is one of the points on line CD, and is also on segment AB. Because it is on CD, we know it is the same distance from A as from B. That means AM = BM, and M is the midpoint of AB.
__
Points B, C, D are not on the same line, so can form a triangle. As with any triangle, the sum of any two segments is greater than the length of the third. Here, this is expressed as CB + BD > CD.
__
With some work using the Pythagorean theorem, you can show that ...
CM = AM×√3
Similarly, MD = BM×√3.
Adding these two relations tells us ...
CM +MD = √3(AM +BM)
CD = AB×√3 . . . . . AB and CD are not the same length
__
AM and BM are on the same line, so cannot be perpendicular to each other.
_____
Additional comment
When you are studying compass and straightedge constructions, you would do well to actually perform these constructions using those tools on paper. This gives you a feel for what is going on and helps you remember the steps. A computer screen is no substitute for hands-on.
While in Mexico, Kirsten bought 5 pottery bowls for $55. Solve the equation 5c = 55 to find the cost of each bowl.
Answers
Answer:
Each bowl costs $11
Step-by-step explanation:
5c = 55
To solve, divide each side by 5:
( 5c / 5 ) = ( 55 / 5 )
c = 11
5c=55
/5. /5
C=11
write down a different ratio equivalent to 16:2
Answers
All you need to do is multiply(or divide).
16/2=8
2/2=1
8:1
16x2=32 2x2=4; 16x3=48 2x3=6; 16x4=64 2x4=8;...
32:4; 48:6; 64:8...
hope it helps!
The solids are similar. Find the missing dimension(s).
Will mark brainlest if you give a full explanation 10 min!!!

Answers
Answer:
s = 4.5 cm
l= 3.75 cm
Step-by-step explanation:
Mathematically, when two shapes are similar, the ratio of their corresponding sides are equal
According to this rule, we have it that;
4/6 = 3/s
4 * s = 3 * 6
4s = 18
s = 18/4
s = 4.5 cm
Similarly;
4/5 = 3/l
4 * l = 5 * 3
4l = 15
l = 15/4
l = 3.75 cm
Ian has $6,000.00 to invest for 2 years. The table shows information about two investments Ian can make.
Ian makes no additional deposits or withdrawals. Which investment earns the greater amount of interest over a period of 2 years?

Answers
Investment X earns the greater amount of interest over a period of 2 years.
What is simple interest?Simple interest is a method of calculating interest on an amount for n period of time with a rate of interest of r. It is calculated with the help of the formula,
SI = PRT
where SI is the simple interest, P is the principal amount, R is the rate of interest, and T is the time period.
Let's consider that Ian invests in X, then:
Principle amount, P = $6,000
Time, T = 2 Years
Rate of Interest, R = 4.5% at simple Interest = 0.045
The interest earned is:
Interest = PRT = $6,000 × 0.045 × 2 = $540
Now, consider that Ian invests in Y, then:
Principle amount, P = $6,000
Time, n = 2 Years
Rate of Interest, R = 4% at Compound Interest = 0.04
The interest earned is:
Interest = P(1+R)ⁿ - P
= $6,000(1+0.04)² - $6,000
= $489.6
Since $540>$489.6, therefore, Investment X earns the greater amount of interest over a period of 2 years.
Learn more about Simple Interest here:
https://brainly.com/question/2793278
#SPJ1
Which graph represents a quadratic function with a vertex at (0,0)
Answers
Answer:
the graph of x²
Step-by-step explanation:
The graph of x² has a vertex with coordinates (0,0)
A circle has a radius of 7 in. Find the radian measure of the central angle 0 that intercepts and arc of length 15 in.
Do not round any intermediate computations, and round your answer to the nearest tenth.
Answers
The measurement of the central angle is 2.15 radians.
What is central angle?
The central angle is a circle-shaped angle with two arms and a vertex in the centre. The circle's arc is intersected by the two arms of the circle's two radii twice. The central angle can be used to divide a circle into sectors.
Given:
The radius of the circle is 7 in
Length of the arc = 15 in
For solving the problem we followed the formula given below
s = rθ
s is the length of arc, θ is the central angle, and r is the radius of the circle.
So, 15 = 7θ
Or, θ = 15/7
Or, θ = 2.142 radians ≈ 2.15
Hence, the measurement of the central angle is 2.15 radians.
To learn more about central angle from the given link
https://brainly.com/question/10945528
#SPJ1
what is the measure of
A. 140 degrees
B. 20 degrees
C. 160 degrees
D. 90 degrees

Answers
A museum roomcircular in shape, has 5 equally spaced sensors on its walls. There are no dead or overlapping spots along the perimeter of the roomEach sensor has the same angle of detection What is the detection angle of each sensor ? Enter your answer in the box plsss help asap
Answers
Answer: 108 degrees.
Step-by-step explanation:
I think this is how you solve it:
A circle has a total of 360 degrees.
Having 5 equally placed sensors with a certain detection angle means that the sensors form a regular pentagon.
Finding the measure of the interior angles of a regular pentagon can be found using the formula
(180(n-2))/n, with n being the number of vertices of the polygon.
180(5-2)/5 ; 180(3)/5 ; 540/5 = 108
I think this means the detection angle is 108 degrees. Hope this helps!
If you get it wrong I'm terribly sorry T-T
Craig is learning to identify local birds with a Field Guide to Forest Birds deck of cards. He
randomly selects one card from the deck, puts it back in the deck, and selects another card.
He repeats this several times and gets 4 hummingbirds, 3 falcons, 1 woodpecker, 4 owls, 3
loons, and 2 eagles.
Based on the data, what is the probability that the next card Craig selects will be a falcon
card?
Write your answer as a fraction or whole number.
Answers
The probability helps us to know the chances of an event occurring. The probability that the next card Craig selects will be a falcon
card is 3/17.
What is Probability?The probability helps us to know the chances of an event occurring.
\(\rm Probability=\dfrac{Desired\ Outcomes}{Total\ Number\ of\ outcomes\ possible}\)
Given that Craig gets 4 hummingbirds, 3 falcons, 1 woodpecker, 4 owls, 3
loons, and 2 eagles. Therefore, a total of 17 possible outcomes. Now, since the number of outcomes which are falcon is 3. Therefore, the probability of the next card being a falcon can be written as,
\(\rm Probability=\dfrac{Desired\ Outcomes}{Total\ Number\ of\ outcomes\ possible}\)
\(\rm Probability = \dfrac{\text{Number of falcon cards}}{\text{Total number of possible outcomes }} = \dfrac{3}{17}\)
Hence, the probability that the next card Craig selects will be a falcon
card is 3/17.
Learn more about Probability:
https://brainly.com/question/795909
#SPJ1
a type of medicine is given in a 100 miligram dosage. the medicine comes in a 12 gram bottle. how many 100 milligram doses are in a bottle?
Answers
The medicine bottle has 120 doses of 100 miligram each.
As per the known fact, 1000 miligram is 1 gram. So, the amount of medicine in the bottle in milligrams = 12×1000
Performing multiplication on Right Hand Side of the equation
Amount of medicine in bottle = 12000 milligrams.
Now, number of dose of 100 miligram medicine = 1
Amount of dose of 12000 miligram medicine = (1/100)×12000
Performing division and multiplication on Right Hand Side of the equation
Amount of doses in 12000 miligram medicine = 120
Thus, there are 120 doses in a medicine.
Learn more about dosage calculations -
https://brainly.com/question/24793154
#SPJ4
You look over the songs in a jukebox and determine that you like 14
of the 53 songs.
(a) What is the probability that you like the next four songs that are played? (Assume song cannot be repeated.)
(b) What is the probability that you do not like the any of the next four songs that are played? (Assume song cannot be repeated.)
Answers
The probability that all four songs are liked will be 0.03418 and the probability of not liking the next four songs will be 0.99658.
What is probability?The probability of an event occurring is defined by probability.
Probability is also called chance because if you flip a coin then the probability of coming head and tail is nothing but chances that either head will appear or not.
As per the given,
Total songs = 53
Like songs = 14
Probability of selecting and liking the first song = 14/53
Now since repetition is not allowed and one like the song has been chosen out of 14 thus, the remaining songs = 13, and total songs = 43 - 1 = 52
Probability of selecting liking the second song = 13/52
Probability of selecting liking the third song = 12/51
Probability of selecting liking the fourth song = 11/50
a)
The probability of liking all songs will be 14/53 x 13/52 x 12/51 x 11/50 = 0.03418.
b)
The probability of not liking the next four songs =1 - The probability of liking all songs
The probability of not liking the next four songs = 1 - 0.03418 = 0.96582.
Hence "The probability that all four songs are liked will be 0.03418 and the probability of not liking the next four songs will be 0.99658".
For more information about the probability,
brainly.com/question/11234923
#SPJ1
a college runner set a school record of 3 minutes and 59.37 seconds in the mile run. assuming that the distance was measured accurately to five significant figures, what was the runner's average speed in kilometers per hour? assume 1 km
Answers
The runner's average speed in kilometers per hour is 24.257 km.
The total distance covered by the runner is 1 mile. The relation between kilometers and miles is given as 1 km = 0.62 mi. Converting 1 mile to km by using the given relation, we get-
Distance = 1 mile
= 1 mile × [1 km/0.62 mile]
= 1.6129 km
The time taken to complete a 1-mile run is 3 minutes and 59.37 seconds. The relation between hours and minutes is given below.
1 hour = 60 minutes ……(1)
Converting 3 minutes to hours using equation (1), we get-
3 minutes = 3 minutes × [1 hour/60 minutes]
= 0.05 hours
The relation between hours and seconds is given below.
1 hour = 3600 second …….(2)
Converting 59.37 seconds to hours using equation (2), we get-
59.37 seconds = 59.37 seconds × [1 hour/3600 seconds]
= 0.016492 hours
Total time to cover 1 mile = (0.05 + 0.016491) hours = 0.066492 hours
The average speed of the runner is calculated by the following relation-
Average Speed = Distance (km)/time (hours)
= 1.6129 km/0.066492 hours
= 24.257 km/hour
Therefore, the average speed in kilometers per hour is 24.257km.
For more such questions on average speed
https://brainly.com/question/12322912
#SPJ4
There are 625 students in Weaver Junior High School. Jimmy surveyed the 30 students in his English class regarding their favorite subject. Twenty-four of the students responded that they liked history best. If his class is a representative sample of the entire school, how many students in the school could Jimmy predict would choose history as their favorite subject?
Answers
Answer:
I love you too luv uip basin MA unsa ka luv Amfing ara luv ha ayaw pod tawn ana man
The number of students in the school could Jimmy predict would choose history as their favorite subject is 500.
What is random sampling?In statistics, a simple random sample is a subset of people chosen at random from a larger group, all of whom were chosen with the same probability. It is a method of choosing a sample at random.
Given that, there are 625 students in Weaver Junior High School.
24 of the 30 students surveyed liked history.
The students surveyed liked history
=24/30 ×100
= 0.8×100
= 80%
Now, 80% of 625 students
625 × 0.8 = 500
So, 500 of the total students like history
Therefore, the number of students in the school could Jimmy predict would choose history as their favorite subject is 500.
Learn more about the random sample here:
https://brainly.com/question/12719656.
#SPJ6
The mean value of land and buildings per acre from a sample of farms is $1400, with a
standard deviation of $200.
The data set has a bell-shaped distribution. Assume the number of farms in the sample is 74.
(a) Use the empirical rule to estimate the number of farms whose land and building values per acre are between $1000 and $1800.
___ farms (Round to the nearest whole number as needed.)
Answers
Answer:
In this case, the mean is $1400, and the standard deviation is $200.
So, one standard deviation of the mean is 1400+200= $1600 and 1400-200 = $1200.
Therefore, according to the empirical rule, approximately 68% of the farms will have land and building values per acre between $1200 and $1600.
To estimate the number of farms that fall within this range, we can multiply the total number of farms (74) by 0.68.
(74)*(0.68) = 50.32 or about 50 farms
So, according to the empirical rule, approximately 50 farms will have land and building values per acre between $1000 and $1800.
two cars start moving from the same point. one travels south at 56 mi/h and the other travels west at 42 mi/h. at what rate (in mi/h) is the distance between the cars increasing four hours later?
Answers
Answer:
Step-by-step explanation:
56 divided by 42 is your awnser
Consider the following.C = x3 − 10x2 + 33xUse the cost function to find the production level at which the average cost is a minimum.x =For this production level, show that the marginal cost and average cost are equal.marginal cost $average cost $
Answers
As the marginal cost and average cost are both equal to $8 at x = 5, we can conclude that the marginal cost and average cost are equal at this production level.
To find the production level at which the average cost is a minimum, we need to first find the average cost function. The average cost function is given by:
\(AC(x) = C(x)/x\)
Substituting C(x) from the given equation, we get:
\(AC(x) = (x^3 - 10x^2 + 33x)/x\)
Simplifying this, we get:
\(AC(x) = x^2 - 10x + 33\)
To find the production level at which the average cost is a minimum, we need to find the value of x that minimizes the average cost function. We can do this by taking the derivative of the average cost function and setting it equal to zero:
\(d/dx (x^2 - 10x + 33) = 2x - 10 = 0\)
Solving for x, we get:
x = 5
Therefore, the production level at which the average cost is a minimum is x = 5.
To show that the marginal cost and average cost are equal at this production level, we need to first find the marginal cost function. The marginal cost function is given by the derivative of the cost function:
\(MC(x) = d/dx (x^3 - 10x^2 + 33x) = 3x^2 - 20x + 33\)
Substituting x = 5, we get:
\(MC(5) = 3(5)^2 - 20(5) + 33 = 8\)
Therefore, the marginal cost at x = 5 is $8.
To find the average cost at x = 5, we can substitute x = 5 into the average cost function:
\(AC(5) = 5^2 - 10(5) + 33 = 8\)
Therefore, the average cost at x = 5 is also $8.
Since the marginal cost and average cost are both equal to $8 at x = 5, we can conclude that the marginal cost and average cost are equal at this production level.
To know more about marginal cost refer here:
https://brainly.com/question/15575229
#SPJ11