Answers
Answer:
sont yell at me the answer is the secoiund one
Step-by-step explanation:
Related Questions
Solve the system of equations by substitution.
3x+2y=10 y=3x-4
x= y=
Answers
Answer:
x=2; y=2
Step-by-step explanation:
3x+2y=10
y=3x-4
We can substitute y from the first equation with the second equation:
3x+2(3x-4)=10
3x+6x-8=10
9x=18
x=2
Now plug this in to any of the equations (i used second equation):
y=3(2)-4
y=6-4
y=2
Check your answers:
y=3x-4
2=3(2)-4
2=6-4
2=2
Please help first correct answer gets brainleist and 100 points please I'll answer your questions

Answers
Answer:
a) AE and BC are parallel (as shown by the markings)
b) ED and CD are equal in length (as shown by the markings)
c) 3: AE is perpendicular AB, AB is perpendicular to AE/AC, AC is perpendicular to AB
FP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
fav singer??
I like XXXTentacion and Trippie Redd
Answers
Answer:
Samee
Step-by-step explanation:
Answer:
TIAGZ
and Billie Eilish
DABABY
Step-by-step explanation:
Heyy guys I need help

Answers
===================================================
Explanation:
Since AE = BE, we know that triangle ABE is isosceles with A = B as the congruent base angles (it might help to rotate the triangle 90 degrees clockwise). The congruent base angles are always opposite the congruent sides of an isosceles triangle.
Focus on triangle ABE. Let's find the missing angle E.
A+B+E = 180
55+55+E = 180
110+E = 180
E = 180-110
E = 70
So angle BEA = 70 degrees
This means angle DEC is also 70 degrees. Angles BEA and DEC are congruent vertical angles.
--------------------
Now focus on triangle DEC. We just found E = 70. The diagram shows D = 34. Use these items to find C
D+E+C = 180
34+70+C = 180
104+C = 180
C = 180-104
C = 76
Angle C is 76 degrees
Answer:
hey
Step-by-step explanation:
I’m not sure I need help

Answers
Answer:
D) \(1 < x\leq 4\)
Step-by-step explanation:
1 is not included, but 4 is included, so we can say \(1 < x\leq 4\)
prove that the intersection of any two distinct eigenspaces of a matrix a is {0}.
Answers
We have proved that the intersection of any two distinct eigenspaces of a matrix A is {0}.
Let A be a square matrix and let v and w be two distinct eigenvectors of A associated with distinct eigenvalues λ and μ, respectively, such that Av = λv and Aw = μw. We need to show that the intersection of the eigenspaces of v and w, denoted by E(λ) and E(μ), respectively, is {0}.
Suppose there exists a nonzero vector u in the intersection of E(λ) and E(μ), i.e., u ∈ E(λ) ∩ E(μ). Then, by definition, Au = λu and Au = μu. Thus, we have λu = μu, which implies (λ - μ)u = 0. Since λ and μ are distinct, we have (λ - μ) ≠ 0. Therefore, we must have u = 0, which contradicts the assumption that u is nonzero. Thus, the intersection of E(λ) and E(μ) must be {0}.
Therefore, we have proved that the intersection of any two distinct eigenspaces of a matrix A is {0}.
for such more question on intersection
https://brainly.com/question/11589195
#SPJ11
Let A be an n x n matrix and let λ1 and λ2 be distinct eigenvalues of A with corresponding eigenvectors v1 and v2, respectively. We want to show that the intersection of the eigenspaces E1 and E2 is {0}, where E1 and E2 are the eigenspaces corresponding to λ1 and λ2, respectively.
Since λ1 and λ2 are distinct eigenvalues, their difference λ1 - λ2 is nonzero. Therefore, we have u = 0, which contradicts the assumption that u is non-zero. Hence, the intersection of any two distinct eigenspaces of A is {0}.
Learn more about matrix here : brainly.com/question/29132693
#SPJ11
A building casts a 33 m shadow when the Sun is at an angle of 26. to the vertical. How tall is the the building, to the nearest meter? Use a trigonometric ratio to find the distance FE. A building casts a 33 m shadow when the Sun is at an angle of 26. to the vertical. How tall is the building, to the nearest meter? Use a trigonometric ratio to find the distance F E.

Answers
so basically we just us do this
tan(26)=33/FE
Multiply to get rid of fraction
tan(26)FE=33
divide to get FE alone
FE = tan(26) * 33
FE=16.0951m
so it should be 16.0951m
A mathematician is wondering what would happen to the surface area of a square if you were to repeatedly cut the square in half. She concludes that the surface area would become less and less but would never become zero units\(^2\). Which equation would help her model the surface area of a square piece of paper as it was repeatedly cut?
a) \(y=x^2+4x-16\)
b) \(y=-25x^2\)
c) \(y=9(2)^x\)
d) \(y=36(\frac{1}{2})^x\)
Answers
The equation that would help the mathematician model the surface area of a square piece of paper as it was repeatedly cut is \(y = 36 \times \frac{1}{2}^x\)
Option D is the correct answer.
We have,
In this equation, the variable x represents the number of times the square is cut in half, and y represents the surface area of the square.
As x increases, the exponent of 1/2 decreases, causing the value of y to decrease.
This exponential decay accurately represents the idea that the surface area becomes less and less but never reaches zero units²
Thus,
The equation that would help the mathematician model the surface area of a square piece of paper as it was repeatedly cut is \(y = 36 \times \frac{1}{2}^x\).
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
The correct equation that would help model the surface area of a square piece of paper as it is repeatedly cut in half is: \(\(y=36(\frac{1}{2})^x\)\)
As the square is cut in half, the side length of the square is divided by 2, resulting in the area being divided by \(\(2^2 = 4\)\).
Therefore, the equation \(y=36(\frac{1}{2})^x\)\)accurately represents the decreasing surface area of the square as it is repeatedly cut in half.
and, \(\(y=x^2+4x-16\)\)is a quadratic equation that does not represent the decreasing nature of the surface area.
and, \(\(y=-25x^2\)\) is a quadratic equation with a negative coefficient.
and, \(\(y=9(2)^x\)\)represents exponential growth rather than the decreasing nature of the surface area when the square is cut in half.
Learn more about Equation here:
https://brainly.com/question/29657983
#SPJ1
what is the probability of drawing two blue cards if the first one isn’t placed back in the bag before the second draw
Answers
Answer: You need more information to solve this.
Step-by-step explanation:
a= how many cards you have overall
B= how many blue cards there are
C= how many blue cards you have after you took one out
D= how many cards you have overall after you took one out
B/a*C/D= your answer
11x26
49x12
12x25
Thanks for helping me!
Answers
588
300
:) your welcome
Answer:
1. 286
2. 588
3.300
HELPPP PLZ PIECEWISE FUNCTIONS

Answers
Answer: f(4)=17
Step-by-step explanation:
Plug 4 into 5x-3, as this includes 4 in the domain.
5(4)-3=17
Plz help me with 6th grade math- I’m dumb

Answers
A bag contains 4 purple beads and 3 green beads. A bead is drawn and then replaced before drawing the second bead. Find the probability both beads drawn are green.
A) 16/49
B) 6/7
C) 6/49
D) 9/49
Answers
Answer:
9/49
Step-by-step explanation:
4 purple beads and 3 green beads= 7 beads
P( green) = green = total = 3/7
Replace the bead
4 purple beads and 3 green beads= 7 beads
P( green) = green = total = 3/7
P( green , replace, green) = 3/7 * 3/7 = 9/49
if you pulled once, the probability would be 3/7. multiply 3/7*3/7 to get 9/49
hope this helps!
the attachment is the question

Answers
Answer:
A
Step-by-step explanation:
Answer: A
Step-by-step explanation:
Joann decides to paint one wall in her room with blackboard paint. The wall has the dimensions shown. A can of paint covers 25 square feet. How many cans of blackboard paint does Joann need for the wall.
Answers
*see attachment for the diagram of the wall
Answer:
6 cans
Step-by-step explanation:
First, let's calculate the area of the wall to be painted = area of a rectangle
Area of the rectangle = length*width
From the diagram,
Length = 13 ft
Width = 10 ft
Area = 13*10 = 130 ft²
Given that 1 can of paint covers 25 ft²,
Number of can of paints that will cover 130 ft² = 130/25 = 5.2
This means we will need more than 5 cans. So Joan will need to get roughly 6 cams of blackboard paint.

What is 52s+30b it is on an I ready
Answers
Another representation of the given algebraic expression 52s + 30b as required is; 2 (26s + 15b).
Which expression is equivalent to the given expression 52s + 30b?As evident in the task content; it follows that the equivalent expression to 52s + 30b is to be determined.
Given; 52s + 30b
Since 2 is a common factor to both terms of the equation; we have that;
2 (26s + 15b)
Ultimately, the equivalent expression is; 2 (26s + 15b).
Complete question:
What is 52s+30b in a factorized form.
Read more on equivalent expressions;
https://brainly.com/question/15775046
#SPJ1
Consider this expression. - 4 x 2 + 2 x − 5 ( 1 + x ) What expression is equivalent to the given expression? x 2 + x +
Answers
The expression equivalent to\(-4x^2 + 2x - 5(1 + x)\) is \(4x^2 + 8x + 5.\)
This expression matches the form \(x^2 + x + c,\) where c = 5.
To simplify the given expression \(-4x^2 + 2x - 5(1 + x)\) and make it equivalent to the expression \(x^2 + x + c,\) where c is a constant term, we need to perform some algebraic operations.
First, let's distribute the -5 to the terms inside the parentheses:
\(-4x^2 + 2x - 5 - 5x\)
Next, we can combine like terms:
\(-4x^2 + (2x - 5x) - 5 - 5x\)
Simplifying further:
\(-4x^2 - 3x - 5 - 5x\)
Now, let's rearrange the terms to match the form \(x^2 + x + c:\)
\(-4x^2 - 3x - 5x - 5\)
To make the leading coefficient positive, we can multiply the entire expression by -1:
\(4x^2 + 3x + 5x + 5\)
Now, we can combine the x-terms:
\(4x^2 + 8x + 5\)
So, the expression equivalent to \(-4x^2 + 2x - 5(1 + x)\) is \(4x^2 + 8x + 5.\)This expression matches the form \(x^2 + x + c,\) where c = 5.
It's important to note that the original expression and the equivalent expression have different coefficients and constants, but they represent the same mathematical relationship.
For similar question on expression.
https://brainly.com/question/723406
#SPJ8
if a and b are independent events with p(a) = 0.65 and p(a ∩ b) = 0.26, then, p(b) =
Answers
The chance of the event B is 0.4 when using the probability for the two independent two event formula.
In the given question, if a and b are independent events with p(a) = 0.65 and p(a ∩ b) = 0.26, then we have to find the value of p(b).
Events classified as independent do not depend on other events for their occurrence.
Event A's likelihood of happening is P(A)=0.65.
The likelihood of the two events A and B intersecting is P(A∩B)=0.26.
Given that the likelihood of the two independent events is:
P(A∩B) = P(A)⋅P(B)
Then the probability of the event B will be,
P(B) = P(A)/P(A∩B)
P(B) = 0.65/0.26
P(B) =0.4
To learn more about independent events link is here
brainly.com/question/13488890
#SPJ4
What is the value of 11p10?
Please answer. No links! & I will mark you as brainless!
Answers
The value of 11p10 is 39,916,800.If "p" represents the permutation function, typically denoted as "P(n, r)" or "nPr," it signifies the number of ways to arrange "r" objects taken from a set of "n" distinct objects without repetition.
The value of 11p10 can be determined by applying the concept of permutations. In mathematics, permutations represent the number of ways to arrange a set of objects in a particular order.
In the expression 11p10, the number before "p" (11) represents the total number of objects, while the number after "p" (10) represents the number of objects to be arranged.
Using the formula for permutations, the value of 11p10 can be calculated as:
11p10 = 11! / (11 - 10)!
= 11! / 1!
Here, the exclamation mark denotes the factorial function, which means multiplying a number by all positive integers less than itself down to 1.
Simplifying further:
11! / 1! = 11 * 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 / 1 = 39,916,800.
In this case, 11p10 would represent the number of permutations of 10 objects taken from a set of 11 objects. However, without more details or the specific values of "n" and "r," the numerical value cannot be determined.
For more such questions on Permutation function:
https://brainly.com/question/30959313
#SPJ8
Given function f(x) = x^3 + 2x, find value of x = c that satisfies Mean-Value Theorem on the interval [- 1,1].
Answers
Answer:
The solution is:
\(\begin{equation*} x=\pm\frac{\sqrt{3}}{3} \end{equation*}\)Step-by-step explanation:
First, we'll calculate the function's average rate of change over [-1,1] as following:
\(\begin{gathered} \frac{f(-1)-f(1)}{-1-1}=-\frac{f(-1)-f(1)}{2}=-\frac{-3-3}{2}=\frac{6}{2}=3 \\ \end{gathered}\)Now, we make f'(x) = 3 and solve for x, as following:
\(\begin{gathered} f^{\prime}(x)=3x{}^2+2=3 \\ \\ \rightarrow3x^2=1\rightarrow x^2=\frac{1}{3}\rightarrow x=\pm\frac{1}{\sqrt{3}} \\ \\ \Rightarrow x=\pm\frac{\sqrt{3}}{3} \\ \end{gathered}\)Therefore, we can conlcude that the solution is:
\(\begin{equation*} x=\pm\frac{\sqrt{3}}{3} \end{equation*}\)The table below shows data for a class's midterm and final exam. Use the table to answer the following questions. Mid-Term Final 100 98 100 95 100 93 95 91 95 88 92 82
9278 88 78 85 65 75 60 What is the 5 number summary for the class's Final Exam? Minimum
type your answer... Lower Quartile type your answer.... Median type your answer... Upper Quartile type your answer...
Maximum
type your answer...

Answers
Based on the scores in the final exam, the five number summary of the class is:
Minimum = 60Lower quartile = 71.5.Median = 85.Upper Quartile = 94.Maximum = 98What is the five number summary for the final exams?The minimum is the smallest score of 60. The maximum will be the largest score of 98.
The lower quartile can be found by the formula:
= (Second score + Third score) / 2
= (65 + 78) / 2
= 71.5.
The upper quartile is:
= (Third to last score + Second to last score) / 2
= (93 + 95) / 2
= 94
The median is:
= (5th score + 6th score) / 2
= (82 + 88) / 2
= 85
Find out more on the five number summary at https://brainly.com/question/24809873.
Point I is on line segment HJ. Given HJ = 15 and IJ
HI.
10, determine the length
Answers
Answer:
Point I is on line segment HJ; which means HI and IJ are equal.
HJ = 15
IJ = 10
Finding the length of HI, given the above statements:
Length of HI = 10 (reason: HI and IJ are congruent)
Solve for x
Please explain step by step

Answers
Answer:
x=16Step-by-step explanation:
Since RQTS is a parallelogram
\(\angle Q +\angle T=180^{o}\)
\(3x+5+9x-17=180^o\)
\(12x-12=180^o\)
\(12x-12+12=180+12\)
\(12x=192\)
\(\cfrac{12x}{12}=\cfrac{192}{12}\)
\(x=16\)
Hope it helps!
Question 5 of 10
Which pair of functions are inverses of each other?
O A. f(x) = 2 + 15 and g(x) = 12x - 15
O B. f(x) = √3x and g(x) = () ³
O c. f(x) = 3 - 10 and g(x) = +10
3
D. f(x) = 11x-4 and g(x) = +4

Answers
The correct answer is D. f(x) = 11x - 4 and g(x) = (x + 4)/11
To determine which pair of functions are inverses of each other, we need to check if the composition of the functions results in the identity function, which is f(g(x)) = x and g(f(x)) = x.
Let's test each option:
Option A:
f(x) = x/2 + 15
g(x) = 12x - 15
f(g(x)) = (12x - 15)/2 + 15 = 6x - 7.5 + 15 = 6x + 7.5 ≠ x
g(f(x)) = 12(x/2 + 15) - 15 = 6x + 180 - 15 = 6x + 165 ≠ x
Option B:
f(x) = ∛3x
g(x) = (x/3)^3 = x^3/27
f(g(x)) = ∛3(x^3/27) = ∛(x^3/9) = x/∛9 ≠ x
g(f(x)) = (∛3x/3)^3 = (x/3)^3 = x^3/27 = x/27 ≠ x
Option C:
f(x) = 3/x - 10
g(x) = (x + 10)/3
f(g(x)) = 3/((x + 10)/3) - 10 = 9/(x + 10) - 10 = 9/(x + 10) - 10(x + 10)/(x + 10) = (9 - 10(x + 10))/(x + 10) ≠ x
g(f(x)) = (3/x - 10 + 10)/3 = 3/x ≠ x
Option D:
f(x) = 11x - 4
g(x) = (x + 4)/11
f(g(x)) = 11((x + 4)/11) - 4 = x + 4 - 4 = x ≠ x
g(f(x)) = ((11x - 4) + 4)/11 = 11x/11 = x
Based on the calculations, only Option D, where f(x) = 11x - 4 and g(x) = (x + 4)/11, satisfies the condition for being inverses of each other. Therefore, the correct answer is:
D. f(x) = 11x - 4 and g(x) = (x + 4)/11
for such more question on inverses
https://brainly.com/question/15066392
#SPJ8
Algebra 2 question matrices. Please help!!
Solve the system of equations below using matrices.

Answers
Answer:
(1, 3, -2) is the answer
Angela Bernice and candice all buy gummy bear weet for 6 p each
Angela buy 2 more gummy bear than bernice
Bernice buy 8 more gummy bear than candice together the three girl have pent £3. 42 on gummy bear
work out how many gummy bear angela buy
Answers
Angela bought 16 gummy bears. It is Based on the data and money angela has.
Candice bought 8 gummy bears and Bernice bought 8 more gummy bears than Candice. Together the three girls spent £3.42 on gummy bears. This means that the cost of one gummy bear is £0.17.
To find the number of gummy bears Angela bought, we can set up a system of equations to represent the given information.
To work out how many gummy bears Angela bought, we can use the equation
8 + 8 + x = £3.42/£0.17where x is the number of gummy bears Angela bought. Solving this equation gives us x = 16. This means that Angela bought 16 gummy bears.
Learn more about Simple Money calculations here:
https://brainly.com/question/13391044
#SPJ4
Work out the bearing of D from C.
D
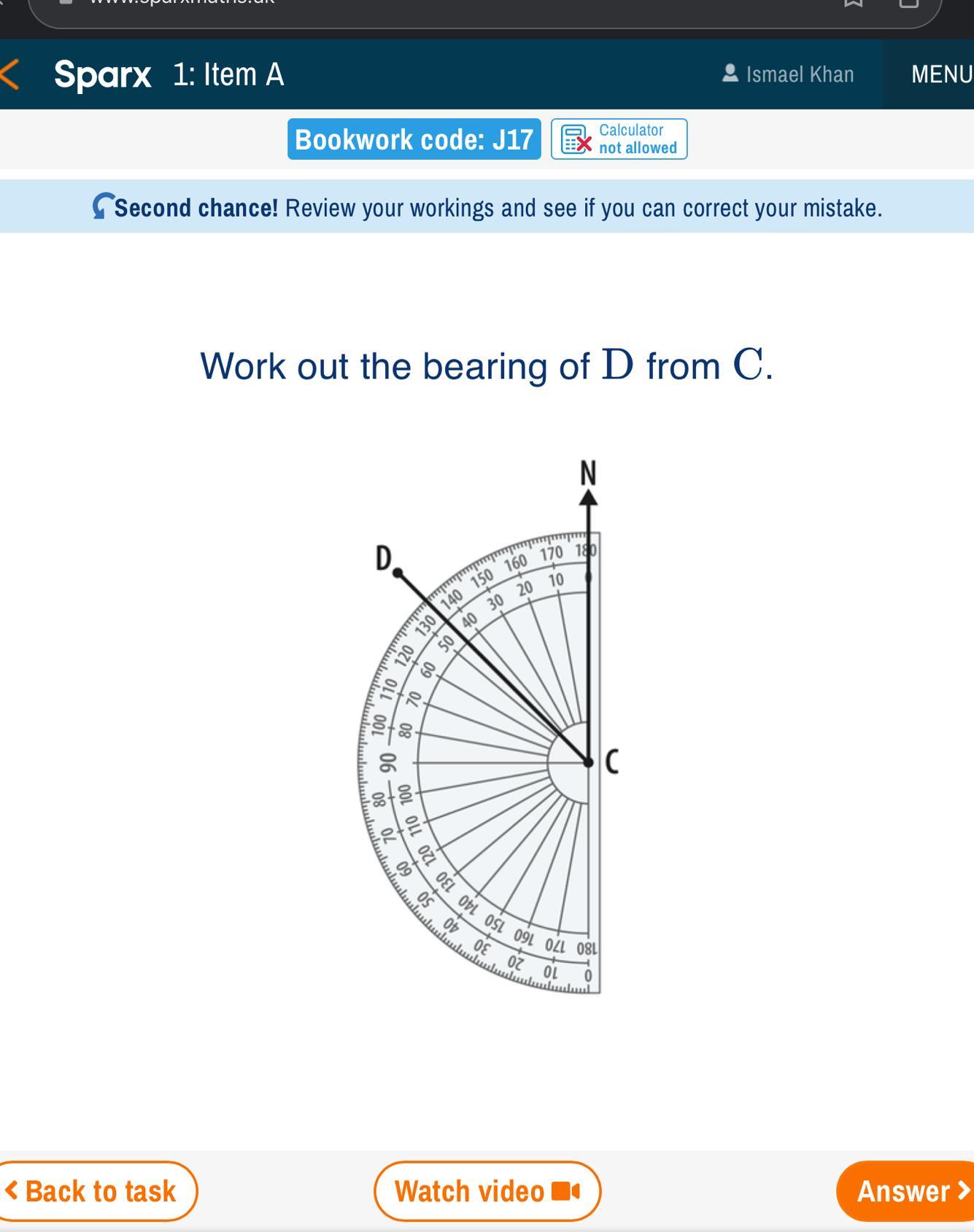
Answers
The bearing of D from C is equal to the angle measure 315°.
What is bearing?Bearing is usually measured in degrees, with 0° indicating the reference direction (usually North), and increasing clockwise to 360°. It refers to the direction or angle between a reference direction and a point or object.
By observation, the angle between the north line CN and the line CD is equal to 45°, the bearing of D from C is the angle formed beginning from the north line clockwise to the line CD calculated as:
360° - 45° = 315°
Therefore, the bearing of D from C is equal to angle measure 315°
Read more about bearing here:https://brainly.com/question/22518031
#SPJ1
The Emotional Intelligence Quotient (EQ) score of a grade 8 class is normally distributed with a mean of 80 and a standard deviation of 20. A random sample of 36 grade 8 learners is selected. Let X be EQ score score of a grade 8 class. It is further known that the probability that the mean EQ score is between x and the population mean is 0.4918. Determine the value if x such that P(x << 80) = 0.4918. Choose the correct answer from the list of options below.
a. 84
b. 80
C. 78
d. 76
e 72
Answers
The given is the Emotional Intelligence Quotient (EQ) score of a grade 8 class is normally distributed with a mean of 80 and a standard deviation of 20, and a random sample of 36 grade 8 learners is selected. The value of x is to be determined such that P(x << 80) = 0.4918.
The population mean is given by μ = 80.The standard deviation of the sample is given by:σ/√n = 20/√36 = 20/6.∴ Standard Error = σ/√n = 20/6 ≈ 3.33.Now, we have to find the z-score associated with a tail probability of 0.4918/2 = 0.2459.Using the standard normal distribution table, we get that the z-value associated with a tail probability of 0.2459 is approximately 0.67.
Now, using the formula for z-score: z = (x - μ) / Standard Error 0.67 = (x - 80) / 3.33 0.67 x 3.33 = x - 80 2.2301 + 80 = x 82.2301 = xThus, the value of x is 82.2301. Therefore, the option (a) 84 and the solution is provided above.
To know more about quotient, visit:
https://brainly.com/question/16134410
#SPJ11
Graph an Integer on a Number Line
Graph -4 on a number line. Then graph 8/2 on a number line. Which one
is greater????
Answers
Answer:
8/2
Step-by-step explanation:
The petersons have two dogs princess and duke .princess eats 2/3of a bag of dog food in a moth duke eats 7/8 of a bag of dog food in a month. How much more dog food does duke eat in a month?
Answers
Answer:
Will you help me plz I will follow you
Answer:
5/24 of a bag I just had this question an thought I'd help you
