Q1
The sum of the first 68 positive odd integers is ?
Q2
The degree of recurrence relation an = 2an-2 + 5an-49 is ??
Q3
In how many ways can an organization containing 19 members elect a president, treasurer and secretary (assuming no person is elected to more than one position)?
Q4
The Greatest Common Divisor (GCD) of 28 × 37 × 58 and 23 × 33 × 54 is ??
Answers
Q1: Sum of first 68 positive odd integers.
Let's represent the first 68 positive odd integers by: 1, 3, 5, 7, ..., 135, 137. The first term, a = 1. The last term, l = 137And, the number of terms, n = 68We need to find the sum of these terms. To find the sum of an arithmetic series, we use the following formula: Sn = n/2[2a + (n-1)d]. Here, d = common difference. Since the given sequence is of odd numbers, the difference between any two consecutive terms is 2. So, d = 2. Put these values in the formula to get: Sn = 68/2[2(1) + (68-1)2], Sn = 34[2 + 135], Sn = 68 × 67Sum of first 68 positive odd integers = 4546.
Q2: Degree of recurrence relation. To find the degree of a recurrence relation, we find the largest value of n in the relation. Here, an = 2an-2 + 5an-49The largest value of n in the relation is n = 49. So, the degree of the recurrence relation is 49.
Q3: Number of ways to elect office bearers in an organization. Let's assume that the 19 members of the organization are named M1, M2, M3, ..., M19. The president can be elected in 19 ways. After the president is elected, the treasurer can be elected in 18 ways. After the treasurer is elected, the secretary can be elected in 17 ways. Therefore, the total number of ways in which the president, treasurer, and secretary can be elected is:19 × 18 × 17 = 5,814.
Q4: Greatest Common Divisor (GCD)To find the GCD of two numbers, we need to find their prime factors.28 × 37 × 58 = 2² × 7 × 37 × 2 × 29 = 2³ × 7 × 29 × 37Similarly, 23 × 33 × 54 = 23 × 3² × 2 × 3 × 3 × 2 × 3 = 2³ × 3⁵ × 23.
The common prime factors are 2³ and 23. So, the GCD is: 2³ × 23 = 184. The GCD is 184.
To know more about recurrence, click here:
https://brainly.com/question/30479680
#SPJ11
Related Questions
what is the surface area of the cylinder? Use 3.14 for π and round to the nearest hundredth.
height=11 Radius=8 in.2
Answers
The surface area of the cylinder is approximately 951.44 square inches, rounded to the nearest hundredth.
What is the surface area of the cylinder?
To find the surface area of a cylinder, we need to find the sum of the areas of its curved surface (lateral area) and its two circular bases.
The formula for the lateral area of a cylinder is L = 2πrh, where r is the radius and h is the height. The formula for the area of each circular base is B = πr^2.
We are given that the height of the cylinder is 11 inches and the radius is 8 inches. Therefore, we can calculate:
L = 2πrh = 2 × 3.14 × 8 × 11 = 549.52 in²
B = πr^2 = 3.14 × 8^2 = 200.96 in²
The total surface area is the sum of the lateral area and the two base areas:
Surface area = L + 2B = 549.52 + 2(200.96) = 951.44 in²
Hence, the surface area of the cylinder is approximately 951.44 square inches, rounded to the nearest hundredth.
To learn more about surface area of the cylinder, Visit
https://brainly.com/question/27440983
#SPJ1
Please help I'm stuck

Answers
Answer:
a^2+20a+24
Step-by-step explanation:
Answer:
your answer is a^2 + 20a + 24
Step-by-step explanation:
Please help me!
[One Step Inequalities]
![Please help me![One Step Inequalities]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/yY0NgsCqo6GeOfAW4PRA5WB7sMNr6ler.png)
Answers
Answer: B
Step-by-step explanation:
Answer:
x is greater than or equal to 4
Step-by-step explanation:
divide both sides by two, treating it as an equation
so x is greater than or equal to 4
What is the product of –12 and –4?
Answers
Answer:
48
Step-by-step explanation:
-12 x -4 = 48 (When we multiply two negetive numbers, the product becomes positive )
Answer:
48
Step-by-step explanation:
i did the quiz
X + 2x - 7/4=1 - x/2 -x ayudaaaaa
Answers
Answer:
|x| - |-x| = 0
Step-by-step explanation:
Answer:
no se
Step-by-step explanation:
no se
Included in the definition of an elliptic curve is a single element denoted O and called the point at infinity or the ____ .
Answers
Answer:
Zero Point
Step-by-step explanation:
The surface area S of a sphere is a function of its radius r given by S(r) = 4². Find S(2)and S(4). (Round your answers to two decimal places.) S(2) = S(4) Need Help? Read It
Answers
The surface area of a sphere with a radius of 2 units is approximately 50.24 square units, and the surface area of a sphere with a radius of 4 units is approximately 200.96 square units.
To find the surface area of a sphere with radius rr, we can use the formula S(r)=4πr2S(r)=4πr2.
Let's substitute the given values into the formula:
For r=2r=2, we have:
S(2)=4π⋅22S(2)=4π⋅22
S(2)=4π⋅4S(2)=4π⋅4
S(2)=16πS(2)=16π
For r=4r=4, we have:
S(4)=4π⋅42S(4)=4π⋅42
S(4)=4π⋅16S(4)=4π⋅16
S(4)=64πS(4)=64π
Now, let's approximate the values to two decimal places using a calculator:
S(2)≈16⋅3.14≈50.24S(2)≈16⋅3.14≈50.24
S(4)≈64⋅3.14≈200.96S(4)≈64⋅3.14≈200.96
Therefore, S(2)≈50.24S(2)≈50.24 and S(4)≈200.96S(4)≈200.96 (rounded to two decimal places).
learn more about "sphere ":- https://brainly.com/question/10171109
#SPJ11
an iterative algorithm will usually run faster than an equivalent recursive algorithm. true or false
Answers
True, an iterative algorithm will usually run faster than an equivalent recursive algorithm. This is because iterative algorithms use loops to repeat a set of instructions, whereas recursive algorithms call themselves repeatedly until they reach a base case.
An iterative algorithm will usually run faster than an equivalent recursive algorithm. This is because recursive algorithms often involve function calls, which have overhead costs such as saving and restoring the call stack. In contrast, iterative algorithms use loops and do not require the same overhead, making them more efficient in terms of both time and memory usage.
However, it's important to note that some problems may be more elegantly or intuitively solved using recursion, even if it's less efficient. The repeated function calls in a recursive algorithm can lead to slower performance and higher memory usage compared to the more direct approach of an iterative algorithm.
To learn more about iterative algorithm -brainly.com/question/30803208
#SPJ11
Describe the relationship between the area of a circle and it’s circumference
Answers
Answer: We know that for any circle with radius r the formula for the area and circumference of the circle is given as: Area of circle=πr². ... Hence, to describe the relationship between the area of a circle and its circumference. The Area of circle is 1/2 times the radius times the circumference.
Step-by-step explanation:
Solve by using elimination. Express your answer as an ordered pair.

Answers
Greetings again.
The answer is (-3,6)
Explanation:
As explained in the your previous question about eliminating the term.
We can either eliminate x-term or y-term to find/solve another term first. But It's easier to eliminate the term without multiplying to make both terms the same.
By adding/subtracting vertically for two equations. We get that the adding y and -y makes them 0.
Therefore, we eliminate y-term to solve x first.
\(\left \{ {{2x+y=0} \atop {3x-y=-15}} \right. \\5x=-15\\\)
I explained about adding/subtracting vertically.
Basically, 2x+3x = 5x
y - y = 0
0 - 15 = -15
That's how to get 5x = -15
\(x=-3\)
Because it is the system of two linear equations. We need to find the y-term too.
Therefore, substitute x = -3 in any given equations. I suggest you to substitute x = -3 in the equation with less coefficient value.
So I'll substitute x = -3 in 2x+y = 0 instead because the first equation has less coefficient than the second equation.
\(2x+y=0\)
Substitute x = -3 in the equation.
\(2(-3)+y=0\\-6+y=0\\y=6\)
Therefore, when x = -3, y = 6. Since you want the answer as an ordered pair. The answer is (-3,6)
What is the value of x?
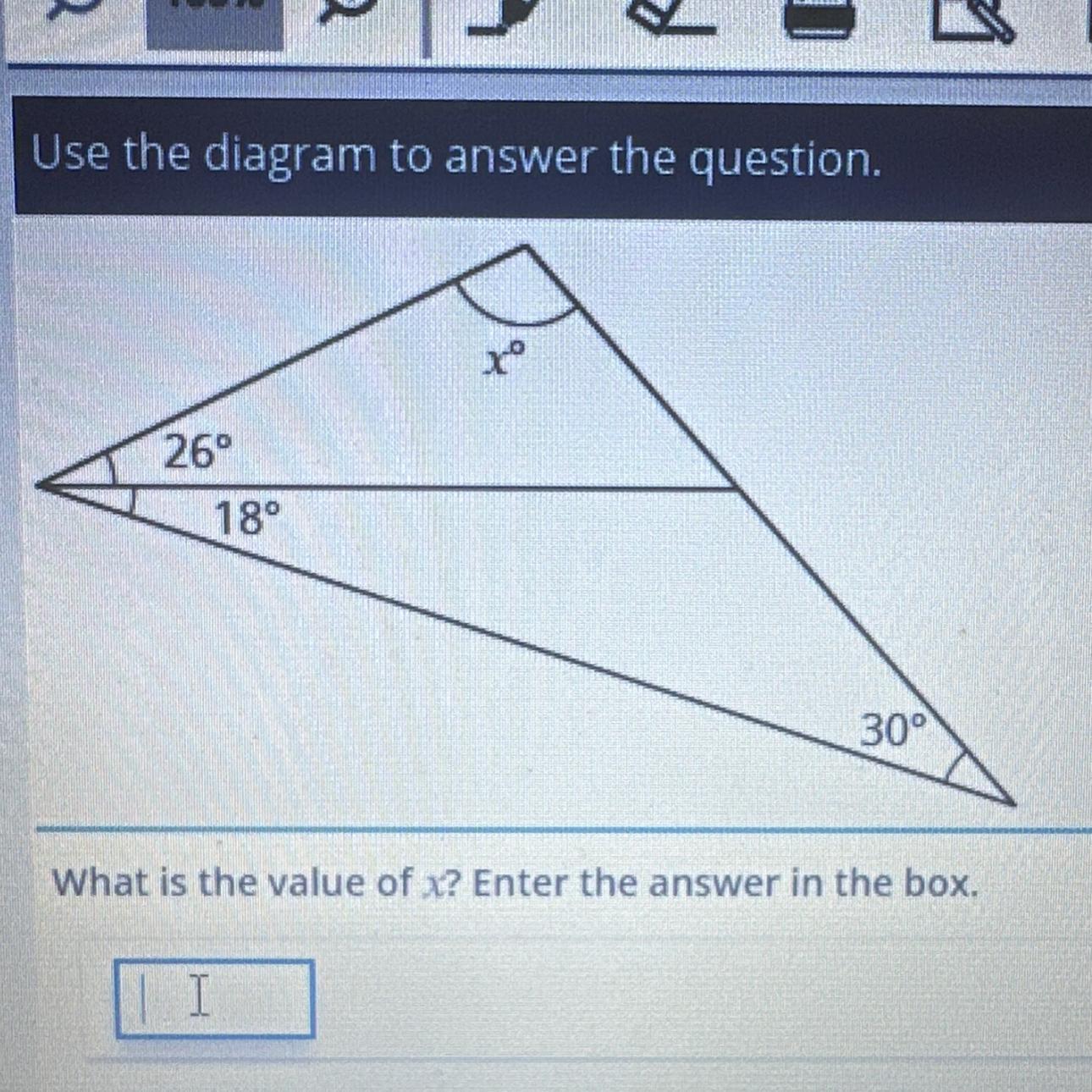
Answers
Answer:
x = 106 degrees
Step-by-step explanation:
we can create a triangle with angles x, 30, and 26+18.
that means x + 30 + (26 + 18) = 180.
move the constants to one side to get x = 180 - 30 - (26 + 18) = 106
Tina and Lane share a 16-ounce box of cereal. By the end of the week, Tina has eaten 3/8 of the box, and Lane has eaten 1/4 of the box of cereal. How many ounces are left in the box?
Answers
Answer:6 ounce of cereal are left in the box
Step-by-step explanation:
Total amount of cereal = 16 ounce
Amount of cereal eaten by Tina= 3/8 X16= 6ounce
Amount of cereal eaten by Lane= 1/4 X16= 4ounce
Amount of cereal left = Total amount of cereal -Amount of cereal eaten by Tina and Lane
=16- ( 6+4)
16-10
= 6 ounce of cereal remaining
Dante and Tania are both math tutors. The amount Dante charges for a session h hours long is represented by the function (h) =
40h + 10. Tania charges a flat fee of $30 plus $15 an hour.
Which statement about the functions is true?

Answers
Answer:
D
Step-by-step explanation:
In the result x2(3) = 8.4, p < 0.05, what is x2? significance level chi square critical value degrees of freedom
Answers
The 3 represent the degree of the freedom in the given equation.
According to the statement
we have to find that the in the given statement the digit is 3 is represented the term and we have to find that term.
So, For this purpose, we know that the
The given statement is:
X^2(3) = 8.4, p < .05,
From this it is clear that the
Degrees of freedom refers to the maximum number of logically independent values, which are values that have the freedom to vary, in the data sample.
This represent the independent values in the given statement also.
So, The 3 represent the degree of the freedom in the given equation.
Learn more about Degrees of freedom here
https://brainly.com/question/17305237
Disclaimer: This question was incomplete. Please find the full content below.
Question:
In the result X^2(3) = 8.4, p < .05, what is 3 represent from the given questions?
a. the observed value
b. the critical value
c. the significant level
d. degrees of freedom
#SPJ4
Need help
1000x+27x+5.5=9236
Answers
Answer:
x = 8.98782862707
Step-by-step explanation:
Base on the given we can infer that we are solving for x:
Given equation:
1000x+27x+5.5=9236
Combine similar terms
1027x + 5.5 = 9236
Subtract both side by 5.5
1027x + 5.5 = 9236
-5.5 -5.5
-------------------------------------
1027x = 9230.5
Now divide both sides by 1027x
9230.5 / 1027
x = 8.98782862707
[RevyBreeze]
Help meeee
16 and 17

Answers
2x+6+x=180
3x+6=180
3x=180-6
3x=174
x=58
2(58)+6 =122
Linear pairs are 180 degree angles
Angle 1 = 58
Angle 2 = 122
suppose the number of cell phone calls made or received per day by cell phone users follows a normal distribution with a mean of 13.1 and a standard deviation of 4.3. use this information to answer questions 6 - 9.
Answers
The probability that a cell phone user makes or receives less than 12 calls per day is 0.3971.
What is probability that user makes or receives less than 12 calls?To find P(x < 12), we need to standardize the value of 12 using the formula: z = (x - μ) / σ where z = z-score, x = value of interest, μ = mean, and σ = standard deviation.
Substituting the values, we get:
z = (12 - 13.1) / 4.3
z = -0.25581
Using a calculator, we can find the probability that z is less than -0.25581, which is:
P(z < -0.25581) = 0.3971
P(z < -0.25581) = 39.71%.
Full question "Suppose the number of cell phone calls made or received per day by cell phone users follows a normal distribution with a mean of 13.1 and a standard deviation of 4.3. Find P (x <12)".
Read more about probability
brainly.com/question/24756209
#SPJ1
746496,62208,5184 What are the next 3 terms?
Answers
Answer:
432, 36, 3
Step-by-step explanation:
Divide each # by 12
Answer: 432, 36, 3
Step-by-step explanation:
You can divide 746,496 by 12 to get 62,208.
You can divide 62,208 by 12 to get 5,184.
You can continue dividing by 12 to get:
5,184 ÷ 12 = 432
432 ÷ 12 = 36
36 ÷ 12 = 3
Therefore, the next three terms are 432, 36, and 3.
I hope this helps!
what has a slope of 15?
Answers
A slope of 15 simply means that the rate of change of the value on the y-axis with respect to the x-axis is equal to 15.
How to calculate or determine the slope of a line?In Mathematics and Geometry, the slope of any straight line can be determined by using the following mathematical equation;
Slope (m) = (Change in y-axis, Δy)/(Change in x-axis, Δx)
Slope (m) = rise/run
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
By substituting an assumed data points into the slope formula, we have the following;
Slope (m) = (80 - 20)/(6 - 2)
Slope (m) = 60/4
Slope (m) = 15.
In this context, we can reasonably infer and logically deduce that a slope of 15 denotes the rate of change of a straight line on a graph.
Read more on slope here: brainly.com/question/3493733
#SPJ1
what is the range of Dan’s car? It’s highway EPA rating is 40mpg and the tank holds 12 gallons
Answers
The range at which Dan's car can go is 3.33 miles
What is range of a car?A car's range is the distance it can travel with the current amount of fuel in the tank.
The vehicle calculates the range based on the amount of fuel, how the accelerator and brakes are used, and how quickly the car is travelling.
The range of a car can be measured in the unit of distance.
Therefore the range of a car can be calculated as;
R = distance per gallon/ number of gallon.
Dan's car is 40mpg and has 12 gallons in it's tank.
Therefore it's range = 40/12
= 3.33miles.
therefore the range of Dan's car is 3.33miles
learn more about range of a car from
https://brainly.com/question/23423168
#SPJ1
write linear equation in slope intercept

Answers
b = 1
equation y=4/1x + 1
What is the quotient of (x3 3x2 5x 3) Ă· (x 1)? x2 4x 9 x2 2x x2 2x 3 x2 3x 8.
Answers
The quotient of expression is \(\rm x^2+2x+3\).
Given that,
Expression; \(\rm\dfrac{ (x^3 + 3x^2 + 5x + 3) }{ (x + 1)}\)
We have to determine,
The quotient of expression?
According to the question,
To determine the quotient of expression following all the steps given below.
Simplify the expression,
\(\rm =\dfrac{ (x^3 + 3x^2 + 5x + 3) }{ (x + 1)}\\\\= \dfrac{ (x^3 + 2x^2 + 3x + x^2+2x+ 3) }{ (x + 1)}\\\\ = \dfrac{ x(x^2+ 2x+ 3) + 1(x^2+2x+ 3) }{ (x + 1)}\\= \dfrac{ (x^2+ 2x+ 3) (x+1) }{ (x + 1)}\\\\= x^2+2x+3\)
Hence, The required quotient of expression is \(\rm x^2+2x+3\).
For more details refer to the link given below.
https://brainly.com/question/12895249
Consider the pth percentile of a continuous random variable. Which of the following statements are always true? Select all that apply. The area under the curve to the left of the pth percentile is equal to (1-p). The area under the curve to the right of the pth percentile is equal to p. The area under the curve to the left of the pth percentile is equal to p. The area under the curve to the right of the ph percentile is equal to (1-p). The pth percentile is positive.
Answers
The correct statements regarding the pth percentile of a continuous random variable are: the area under the curve to the left of the pth percentile is equal to p, and the area under the curve to the right of the pth percentile is equal to (1-p).
In general, when considering the pth percentile of a continuous random variable, the following statements are always true:
1. The area under the curve to the left of the pth percentile is equal to p: This statement is correct. The pth percentile is the value below which p percent of the data falls. Therefore, the area under the curve to the left of the pth percentile represents p percent of the total area.
2. The area under the curve to the right of the pth percentile is equal to (1-p): This statement is also correct. Since the total area under the curve is equal to 1, the remaining area to the right of the pth percentile is (1 - p).
3. The pth percentile is positive: This statement is not necessarily true. The pth percentile can be positive, zero, or negative depending on the distribution of the random variable. It is possible for a significant portion of the data to fall below zero, resulting in a negative pth percentile.
Therefore, the correct statements are:
- The area under the curve to the left of the pth percentile is equal to p.
- The area under the curve to the right of the pth percentile is equal to (1-p).
To know more about percentile refer here:
https://brainly.com/question/1594020#
#SPJ11
What are the vertical and horizontal asymptotes of F x )= 3x 2 x 2 4?
Answers
As given by the question , so here the vertical and horizontal asymptotes are at x = -12 and y = 1.5.
What is vertical asymptote?On a function graph, a vertical asymptote represents the point at which the function is undefined. Take the formula f(x) = 1/x as an illustration. This function's graph exhibits a vertical asymptote at x = 0 since the function is undefined at this value (division by 0 is undefined).
What is horizontal asymptote?A function's horizontal asymptote is a horizontal line on the function graph that the function approaches as the input (x-value) increases or decreases dramatically. Consider the function f(x) = x2 as an illustration. Because the y-values of the function do not converge to a fixed value as x grows very big, the graph of this function lacks a horizontal asymptote.
We must identify the values of x at which the function is undefined in order to determine the vertical asymptotes of the function 3x/(2x+24).So, to find the vertical asymptotes of the function, we need to solve the equation 2x + 24 = 0 for x. so x = -12.
Similarly, To find the horizontal asymptote in case of equal degrees of numerator and denominator i.e 1 in this case, we need to take the ratio of the first coefficients of numerator and denominator respectively which is 3/2 = 1.5.
To learn more about asymptotes visit:
brainly.com/question/12579013
#SPJ4
choose the statement that correctly describes a normal distribution. the approximate percent of values lying within three standard deviations of the mean is 49.85%. approximately 68% of the values are greater than the mean value. the approximate percent of values lying within two standard deviations of the mean is 47.5%. approximately 68% of the values lie within one standard deviation of the mean.
Answers
The statement that correctly describes a normal distribution is, the approximate percent of values lying within three standard deviation of the mean is 49.85%. approximately 68% of the values are greater than the mean value.
For the standard normal distribution, 68% of the observations lie within 1 standard deviation of the mean; 95% lie within two standard deviation of the mean; and 99.9% lie within 3 standard deviations of the mean.
The Standard Normal curve, shown here, has mean 0 and standard deviation 1. If a dataset follows a normal distribution, then about 68% of the observations will fall within of the mean , which in this case is with the interval (-1,1).
In normally distributed data, about 34% of the values lie between the mean and one standard deviation below the mean, and 34% between the mean and one standard deviation above the mean. In addition, 13.5% of the values lie between the first and second standard deviations above the mean.
The approximate percent of values lying within three standard deviations of the mean is 49.85%. A. Approximately 68% of the values lie within one standard deviation of the mean.
Therefore,
The statement that correctly describes a normal distribution is, the approximate percent of values lying within three standard deviation of the mean is 49.85%. approximately 68% of the values are greater than the mean value.
To learn more about Standard normal distribution visit :
brainly.com/question/14916937
#SPJ4
To estimate the amount of lumber in a tract of timber, an owner randomly selected seventy 50-by-50-foot squares, and counted
the number of trees with diameters exceeding 12 inches in each square. The data are listed here.
O
Relative Frequency
Relative Frequency
7
9
2
11
9
7
X+S
9
0. 40
0. 35
0. 30
0. 25
0. 20
0. 15
0. 10
0. 05
0. 40
0. 35
0. 30
0. 25
0. 20
0. 15
0. 10
0. 05
8
x + 2s
9
x + 3s
H
Need Help?
7 4 8 10
1
6
5
10
8
748
10 8
USE SALT
5. 526
8
4
9
8
7
(a) Construct a relative frequency histogram to describe the data.
Frequency of lumber
5
Interval
Read It
3. 382 to 11. 961
6
06 9
11 10 11 8 8 10 8 8 12
1. 237 to 14. 106
7
7
11
8 8 10
9
9560
Frequency of lumber
L
77
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
amount of lumber
7 8
to 9. 816
7 7
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
amount of lumber
7 7
10 10 7 4 8 7
(c) Calculates for the data. (Round your answer to three decimal places. )
S = 2. 145
✔timber trees
(b) Calculate the sample mean x as an estimate of μ, the mean number of trees for all 50-by-50-foot squares in the tract.
(Round your answer to three decimal places. )
X = 7. 671
timber trees
Construct the intervals x ±s, x ± 2s, and X + 3s. Calculate the percentage of squares falling into each of the three intervals,
and compare with the corresponding percentages given by the Empirical Rule and Tchebysheff's Theorem. (Round your
interval values to three decimal places. Round actual percentages to two decimal places. )
Actual Percentage
Relative Frequency
X %
Relative Frequency
X %
0. 40
0. 35
0. 30
0. 25
0. 20
0. 15
0. 10
0. 05
X %
0. 40
0. 35
0. 30
0. 25
0. 20
0. 15
0. 10
0. 05
Frequency of lumber
7
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
amount of lumber
Frequency of lumber
at least 0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
amount of lumber
Tchebysheff
at least 75%
at least 89%
%
95
Empirical
≈ 68%
≈ 99. 7%
%
Answers
The amount of lumber in a tract of timber, an owner randomly selected seventy 50-by-50-foot squares, and counted the number of trees with diameters exceeding 12 inches in each square is 16.67
In order to estimate the amount of lumber in a tract of timber, an owner will use a technique called sample size estimation.
By using this data, the owner can then calculate an estimate of the total amount of lumber present in the tract of timber.
In this case, the sample size is 70, the square size is 2500 square feet, and the diameter of the trees is 12 inches. Therefore, the formula becomes:
=> Total Trees = (Number of Trees in Sample / 70) x (2500 / 12).
If we plug in the number of trees counted in each square, we can find the total estimated number of trees in the tract of timber.
If the owner counted 7 trees in the first square, the formula would be
=> (7 / 70) x (2500 / 12) = 16.67.
To know more about diameter here.
https://brainly.com/question/5501950
#SPJ4
Complete Question:
To estimate the amount of lumber in a tract of timber, an owner randomly selected seventy 50-by-50-foot squares and counted the number of trees with diameters exceeding 12 inches in each square. The data are listed here.
7 9 8 10 3 7 7 9 9 11 7 9 5 5 10 10 9 8 2 8 5
Are all perfect cubes also multiples of 3?
Are all multiples of 3 also perfect cubes?
Answers
Answer:
See below
Step-by-step explanation:
I'm not positive that this is right, but I'll try.
No, and no. 6 is not a perfect cube, and that is a multiple of 3.
8 is a perfect cube that is not a multiple of three.
I hope this helps, sorry if I'm wrong.
The joint probability density function of a pair continuous random variables X and Y is given by f(x,y)={ k(6−x−y)
0
for 0
elsewhere
(a) Show that k= 8
1
for which f(x,y) is a joint probability density. (3 points) (b) Find the marginal density of Y. (3 points) (c) Find the conditional density of X given Y=y, and use it to evaluate P(X≤1.5∣Y=3.5)
Answers
(a) The value of k is 81/14 for which f(x, y) is a joint probability density. (b) The marginal density of Y is f_Y(y) = (81/14) (18 - 6y). (c) P(X ≤ 1.5 | Y = 3.5) is approximately 0.1667.
To find the value of k and demonstrate that f(x, y) is a joint probability density function, we need to perform the following steps:
(a) Normalize the joint probability density function:
To find the value of k, we integrate f(x, y) over the entire range of x and y and set it equal to 1.
∫∫f(x, y) dx dy = 1
∫∫k(6 - x - y) dx dy = 1
Since the limits of integration are not provided, we assume that x and y both range from 0 to 6.
∫[0 to 6] ∫[0 to 6] k(6 - x - y) dx dy = 1
Solving this double integral:
\(\[k \int_{0}^{6} (6x - \frac{x^2}{2} - xy) \, dy = 1\]\[k \int_{0}^{6} (6x - \frac{x^2}{2} - xy) \, dy = 1\]\)
\(k[6xy - (x^2)y/2 - (y^2)/2]\) evaluated from 0 to 6 = 1
\(k[36x - 18x^2 + 6]\) evaluated from 0 to 6 = 1
k[(216 - 648 + 6) - (0 - 0 + 6)] = 1
k[174] = 1
k = 1/174 = 81/14
Therefore, k = 81/14.
(b) Finding the marginal density of Y:
To find the marginal density of Y, we integrate the joint probability density function f(x, y) with respect to x over its entire range.
\(f_Y(y)\)= ∫[0 to 6] f(x, y) dx
Substituting the value of k:
\(f_Y(y)\) = (81/14) ∫[0 to 6] (6 - x - y) dx
\(f_Y(y) = (81/14) [6x - (x^2)/2 - xy]\) evaluated from 0 to 6
\(f_Y(y) = (81/14) [(36 - 18 - 6y) - (0 - 0 - 6y)]f_Y(y) = (81/14) (18 - 6y)\)
Therefore, the marginal density of Y is \(f_Y(y) = (81/14) (18 - 6y).\)
(c) Finding the conditional density of X given Y = y and evaluating P(X ≤ 1.5 | Y = 3.5):
The conditional density of X given Y = y is given by:
\(f_{X|Y}(x|y) = f(x, y) / f_Y(y)\)
Substituting the values:
\(f_{X|Y}(x|y) = (81/14) (6 - x - y) / (81/14) (18 - 6y)\\f_{X|Y}(x|y) = (6 - x - y) / (18 - 6y)\)
To evaluate P(X ≤ 1.5 | Y = 3.5), we integrate the conditional density function over the range of x from 0 to 1.5:
P(X ≤ 1.5 | Y = 3.5) = ∫[0 to 1.5] f_X|Y(x|3.5) dx
P(X ≤ 1.5 | Y = 3.5) = ∫[0 to 1.5] (6 - x - 3.5) / (18 - 6(3.5)) dx
P(X ≤ 1.5 | Y = 3.5) = ∫[0 to 1.5] (2.5 - x) / 9 dx
Solving this integral:
P(X ≤ 1.5 | Y = 3.5) = [(2.5x - (x²)/2) / 9] evaluated from 0 to 1.5
P(X ≤ 1.5 | Y = 3.5) = [(2.5(1.5) - (1.5²)/2) / 9] - [(2.5(0) - (0²)/2) / 9]
P(X ≤ 1.5 | Y = 3.5) = (3.75 - 2.25) / 9
P(X ≤ 1.5 | Y = 3.5) = 1.5 / 9
Therefore, P(X ≤ 1.5 | Y = 3.5) is approximately equal to 0.1667.
Learn more about integral here: https://brainly.com/question/31433890
#SPJ11
How do you know which inequality represents a graph?
Answers
In order to determine which inequality represents a graph, you need to look at the inequality and identify if the equation is an open or closed interval. If it is an open interval, it will be represented by a dashed line on the graph. If it is a closed interval, it will be represented by a solid line on the graph.
1. Look at the inequality and identify if the equation is an open or closed interval.
2. If it is an open interval, it will be represented by a dashed line on the graph.
3. If it is a closed interval, it will be represented by a solid line on the graph.
4. Determine the starting and ending points of the inequality, and plot them on the graph.
5. Draw the line that connects the two points, either dashed or solid, depending on whether the interval is open or closed.
6. Shade the area of the graph that is represented by the inequality.
7. Label the graph with the inequality, the points, and the shading.
Learn more about inequality here
https://brainly.com/question/28823603
#SPJ4
six less than twice a number x is 38 whats the value ofx
Answers
Answer:
x=22
Step-by-step explanation:
We would do the opposite so "six less" we would add 6 to 38. 6+38= 44 and "twice a number" we would divide by 2. 44 /2= 22. So the answer would be 22.
Hope this helps! :)
Answer:
Answer is 22
Step-by-step explanation:
38+6=44
44 ÷ 2= 22
:)