Put the quadratic
y=2x^2-4x+2
into the quadratic formula
enter the number that belongs in the green box.
Answers
The quadratic formula for solving quadratic equations of the form ax^2 + bx + c = 0 is:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
To put the quadratic equation y = 2x^2 - 4x + 2 into this formula, we need to identify the values of a, b, and c.
In this case, we have a = 2, b = -4, and c = 2. Substituting these values into the quadratic formula, we get:
x = (-(-4) ± sqrt((-4)^2 - 4(2)(2))) / (2 * 2)
x = (4 ± sqrt(16 - 16)) / 4
x = (4 ± 0) / 4
Simplifying this expression, we get:
x = 1 or x = 1/2
Therefore, the solutions to the quadratic equation y = 2x^2 - 4x + 2 are x = 1 and x = 1/2.
To explain this solution in more detail, we first need to understand the quadratic formula and how it can be used to solve quadratic equations. The quadratic formula is a formula that provides the solutions to any quadratic equation of the form ax^2 + bx + c = 0, where a, b, and c are constants.
In this case, we were given a specific quadratic equation, y = 2x^2 - 4x + 2, and we needed to find its solutions. To do this, we identified the values of a, b, and c and substituted them into the quadratic formula. We then simplified the expression to obtain the solutions, which were x = 1 and x = 1/2.
It is important to be able to use the quadratic formula to solve quadratic equations because many real-world problems can be modeled using quadratic equations. By being able to solve these equations, we can find important information such as the roots, or solutions, of the equation, which can help us make predictions and solve problems.
To know more about quadratic equations refer here:
https://brainly.com/question/30098550#
#SPJ11
Related Questions
Write in slope-intercept form of the line through point P(6,-1) with slope 4
Answers
Answer:
y = 4x - 25
Step-by-step explanation:
y = 4x + b
-1 = 4(6) + b
-1 = 24 + b
-25 = b
which of the following is the best estimate of the square root of 41 ?
6.8
6.5
20.5
6.4
Answers
Answer: 6.4
Step-by-step explanation:
square root of 41 is 6.403124 and so on so round down to 6.4
Prove the identity a p(p−1) ≡ 1 (mod p 2 ), where a is coprime to p, and p is prime. (Hint: Try to mimic the proof of Fermat’s Little Theorem from the notes.)
Answers
To prove this identity, we start with Fermat's Little Theorem, which states that if p is a prime number and a is any integer coprime to p, then a^(p-1) ≡ 1 (mod p).
Using this theorem, we can rewrite the given identity as a^(p-1) * a(p-2) ≡ 1 (mod p^2).
Next, we can multiply both sides by a to get a^(p-1) * a(p-1) ≡ a (mod p^2).
Since a and p are coprime, we can use Euler's Totient Theorem, which states that a^φ(p) ≡ 1 (mod p) where φ(p) is the Euler totient function. Since p is prime, φ(p) = p-1, so a^(p-1) ≡ 1 (mod p).
Using this result, we can rewrite our identity as a^(p-1) * a(p-1) * a^-1 ≡ a^(p-1) ≡ 1 (mod p), which implies that a^(p-1) ≡ 1 (mod p^2).
Therefore, we have proven the identity a p(p−1) ≡ 1 (mod p 2 ), where a is coprime to p, and p is prime.
Visit here to learn more about Fermat's Little Theorem : https://brainly.com/question/30761350
#SPJ11
For an art project you are using a piece of cloth out in the shape of an right triangle What’s the area of the cloth?

Answers
Answer:
18
Step-by-step explanation:
6*6/2 = 18
there are 12 red balls 10 yellow balls 15 green balls what is the probability of drawing two green balls without replacement
Answers
Answer: 7/74
Step-by-step explanation:
P(G)=15/37*14/36
= 1/37*7/2
= 7/74
More about probability :
https://brainly.com/question/27342429
I’m need help with 31 I really need to get this done

Answers
Two ways of writting the linear function are:
y = (2/5)*x - 49/55y - 2x = -49How to find the linear function?A general linear function can be written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
Here we know that the slope is 2/5, replacing that we will get:
y = (2/5)*x + b
We also know that this line passes through (12, -5), then we can replace these values to get:
-5 = (2/5)*12 + b
-5 = 24/5 + b
-5 - 24/5 = b
-25/5 - 24/5 = b
-49/5 = b
Then the linear equation is:
y = (2/5)*x - 49/5
Other form of writting this is the standard form, multiply both sides by 5.
5y = 2x - 49
5y - 2x = -49
Learn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
f(x)=-4x^2-6x+1 find all the real zeros of the quadratic function
Answers
Answer:
The real zeros of the quadratic function f(x) = -4x^2 - 6x + 1 are approximately -0.15 and -1.35.
Step-by-step explanation:
To find the real zeros of the quadratic function f(x) = -4x^2 - 6x + 1, we need to find the values of x that make f(x) equal to zero. We can do this by using the quadratic formula:
x = [-b ± sqrt(b^2 - 4ac)] / 2a
where a, b, and c are the coefficients of the quadratic equation ax^2 + bx + c.
In this case, a = -4, b = -6, and c = 1. Substituting these values into the quadratic formula, we get:
x = [-(-6) ± sqrt((-6)^2 - 4(-4)(1))] / 2(-4)
x = [6 ± sqrt(52)] / (-8)
x = [6 ± 2sqrt(13)] / (-8)
These are the two solutions for the quadratic equation, which we can simplify as follows:
x = (3 ± sqrt(13)) / (-4)
Therefore, the real zeros of the quadratic function f(x) = -4x^2 - 6x + 1 are approximately -0.15 and -1.35.
Solve 54=y−14 please help meeeeee
Answers
Answer:
y=68
Step-by-step explanation:
54=y−14
54+14=y
68=y
determine an expression in terms of m and l for the moment of inertia of the masses about axis a.
Answers
To determine an expression in terms of m and l for the moment of inertia of the masses about axis a, we need some additional information about the configuration of the masses and the axis.
The moment of inertia depends on the distribution of masses relative to the axis of rotation. It is a measure of an object's resistance to rotational motion. The formula for the moment of inertia varies depending on the specific shape and distribution of masses.
If you can provide more details about the arrangement of masses and the axis of rotation, I can help you derive the expression for the moment of inertia in terms of m and l.
To know more about an object's resistance:- https://brainly.com/question/1326950
#SPJ11
Given that R=7x+5Y find Y when X=9 and R=35 give your answer as an improper fraction in its simplest form
Please help
Answers
Answer:
y = -28/5
Step-by-step explanation:
R = 7x +5y
35 = 7(9) + 5y
35 = 63 +5y
-5y= 63- 35
-5y/-5 = 28/-5
Y = -28/5
Answer:
Y = - \(\frac{28}{5}\)
Step-by-step explanation:
Given
R = 7X + 5Y ← substitute X = 9, R = 35
35 = 7(9) + 5Y
35 = 63 + 5Y ( subtract 63 from both sides )
- 28 = 5Y ( divide both sides by 5 )
- \(\frac{28}{5}\) = Y
Project Profit (in million $) Investment (in million $)1 0.50 22 1.40 53 1.70 124 1.10 25 4.00 156 0.60 37 2.50 108 1.10 1BeFair wants to decide which projects to fund so that the total profit will be maximized. Formulate this problem in the space provided on the answer sheet.
Answers
The total profit will be maximized by using the objective function Z = 22x₁ + 53x₂ + 124x₃ + 25x₄ + 156x₅ + 37x₆ + 108x₇ + x₈
To formulate this problem mathematically, we need to define the decision variables, objective function, and constraints.
We will define a binary decision variable, \(x_i\), which indicates whether or not to invest in project i. If \(x_i\) = 1, the project i will be funded, and if \(x_i\) = 0, the project i will not be funded.
The objective is to maximize the total profit earned by investing in the selected projects. Thus, the objective function can be written as:
Maximize Z = 22x₁ + 53x₂ + 124x₃ + 25x₄ + 156x₅ + 37x₆ + 108x₇ + x₈
This objective function adds the profit of all the projects that will be funded based on the decision variable \(x_i\).
The total investment cannot exceed the available investment budget of $1 million, which can be written as:
0.50x₁ + 1.40x₂ + 1.70x₃ + 1.10x₄ + 4.00x₅ + 0.60x₆ + 2.50x₇ + 1.10x₈ <= 1
Additionally, the decision variables are binary, which means that x_i can only be either 0 or 1. Therefore, we can add binary constraints for each decision variable as follows:
x_i = 0 or 1 for i = 1,2,3,4,5,6,7,8
To know more about profit here
https://brainly.com/question/15522421
#SPJ4
a 'scooped' pyramid has a cross-sectional area of x 4 at a distance x from the tip. what is its volume if the distance from tip to base is 5?
Answers
The volume of the 'scooped' pyramid is approximately 26.6667 cubic units.
To find the volume of the 'scooped' pyramid, we first need to determine the area of its base. Since the cross-sectional area of the pyramid is x 4 at a distance x from the tip, we can assume that the area at the tip is zero. This means that the area of the base is 4 times the area at a distance of 5 from the tip (since the distance from tip to base is 5).
Therefore, the area of the base is 4x4 = 16 square units. To find the volume, we can use the formula for the volume of a pyramid, which is:
Volume = (1/3) x Base Area x Height
In this case, the height of the pyramid is 5 units. So, we can substitute the values we have:
Volume = (1/3) x 16 x 5
Volume = 26.6667 cubic units
Know more about pyramid here:
https://brainly.com/question/13057463
#SPJ11
8) Kim rolls a white die and a red die. What is the probability that the sum of her two dice
is 10?
Answers
Answer:
The probability is really close.
Step-by-step explanation:
10/2 = 5. So both die must land on a 5.
Answer:
there is a 18.75% chance of rolling a sum of 10
Step-by-step explanation:
solve for x in the following question 2x - 3 = 1
Answers
Answer:
x = 2
Step-by-step explanation:
2x-3 = 1
use addition property of equality (add 3 to each side to keep balance)
2x = 4
use division property of equality (divide both sides by 2)
4/2 = 2
so,
x = 2
Please mark me brainliest, and I really hope you have a great day!
2x - 3 + 3 = 1 + 3
2x = 4
2x/2 = 4/2
X = 2
So, in conclusion, X is equal to 2.
the diameters of ball bearings are distributed normally. the mean diameter is 126126 millimeters and the standard deviation is 33 millimeters. find the probability that the diameter of a selected bearing is greater than 123123 millimeters. round your answer to four decimal places.
Answers
The probability that the diameter of a selected bearing is greater than 123 millimeters is 0.4641 (rounded to four decimal places).Hence, the correct option is A) 0.4641.
The given question is asking to find the probability that the diameter of a selected bearing is greater than 123 millimeters, when the diameters of ball bearings are distributed normally with the mean diameter of 126 millimeters and the standard deviation of 33 millimeters.
Given, Mean diameter, µ = 126 millimeters
Standard deviation, σ = 33 millimeters
We need to find the probability that the diameter of a selected bearing is greater than 123 millimeters.
Now, the given distribution is a normal distribution. Therefore, to solve the problem, we will use the z-distribution formula, which is:
z = (x - µ) / σ,
where x is the value of the variable, µ is the mean, and σ is the standard deviation.
We will substitute the given values in the above formula,
z = (x - µ) / σ=> z = (123 - 126) / 33=> z = -0.09
Using a standard normal distribution table, the probability that z is greater than -0.09 is 0.4641, which
(z > -0.09) = 0.4641
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
if f(x)=3x and g(x)=x^2 fine (f+g)(x)
Answers
The function arithmetic, if \(f(x)=3x and g(x)\)\(=x^2\), then \((f+g)(x)\) is\(x^2 + 3x\)
What is Function arithmetic?Function arithmetic is a mathematical operation of combining one or more functions to produce a new, equivalent function. Function arithmetic can also involve combining the same function multiple times, such as adding the same function twice, or taking the square root of a function. These operations allow a mathematician to manipulate functions in order to simplify or solve equations. Function arithmetic is also important in calculus, where operations such as differentiation and integration are used to calculate the area under or above a curve.
if\(f(x)=3x\) and \(g(x)=x^2\)then find\((f+g)(x)\)
\((f+g)(x) = f(x) + g(x)\)
\(= 3x + x^2\)
\(= x^2 + 3x\)
To know more about Function Arithmetic, visit:
https://brainly.com/question/22340031
#SPJ1
Which of the following is NOT a voluntary response sample? Choose the correct answer below O A. A survey is taken at a mall by asking passersby if they will fill out the survey O B. A radio station asks for call-in responses to a question concerning city recycling OC. A local dentist asks her patients to fill out a questionnaire and mail it back to determine the quality of the care received during an office visit OD. Quiz scores from a college level statistics course are analyzed to determine student progress State whether the data described below are discrete or continuous, and explain why. The number of donations a charity receives each month Choose the correct answer below. O A. The data are discrete because the data can only take on specific values. O B. The data are continuous because the data can take on any value in an interval. O C. The data are continuous because the data can only take on specific values. D. The data are discrete because the data can take on any value in an interval. O
Answers
The correct answer for the first question is D. The data are discrete because the data can take on any value in an interval.
Quiz scores from a college level statistics course are analyzed to determine student progress. This is not a voluntary response sample because the students taking the quiz are required to participate, and their scores are collected for the purpose of analyzing their progress.
For the second question, the data described, which is the number of donations a charity receives each month, is discrete. Discrete data can only take on specific values and cannot be divided into smaller, meaningful intervals. In this case, the number of donations can only be whole numbers, such as 0, 1, 2, and so on. It cannot take on any value in an interval or be represented by fractions or decimals. Therefore, the data is discrete.
It is important to distinguish between discrete and continuous data when analyzing and interpreting data, as different statistical methods and techniques are used for each type. Discrete data is usually counted or measured in whole numbers, while continuous data can take on any value within a given range or interval.
Know more about discrete here,
https://brainly.com/question/30565766
#SPJ11
Which of the following is a polynomial?

Answers
Answer:
i think option d is the correct answer of this question.
Please help thank you

Answers
Answer:
Step-by-step explanation:
A: dividend;
B: divisor;
C: quotient
find the area of the region between y=x1/2 and y=x1/3 for 0≤x≤1.
Answers
We have to find the area of the region between y=x^(1/2) and y=x^(1/3) for 0≤x≤1.
To find the area of the region between y=x^(1/2) and y=x^(1/3) for 0≤x≤1, we have to integrate x^(1/2) and x^(1/3) with respect to x. That is, Area = ∫0¹ [x^(1/2) - x^(1/3)] dx= [2/3 x^(3/2) - 3/4 x^(4/3)] from 0 to 1= [2/3 (1)^(3/2) - 3/4 (1)^(4/3)] - [2/3 (0)^(3/2) - 3/4 (0)^(4/3)]= 0.2857 square units
Therefore, the area of the region between y=x^(1/2) and y=x^(1/3) for 0≤x≤1 is 0.2857 square units. Note: The question but the answer has been provided in the format requested.
To know more about square units visit:
https://brainly.com/question/2411992
#SPJ11
Pls help it due ASAP
Please show workings also
.....
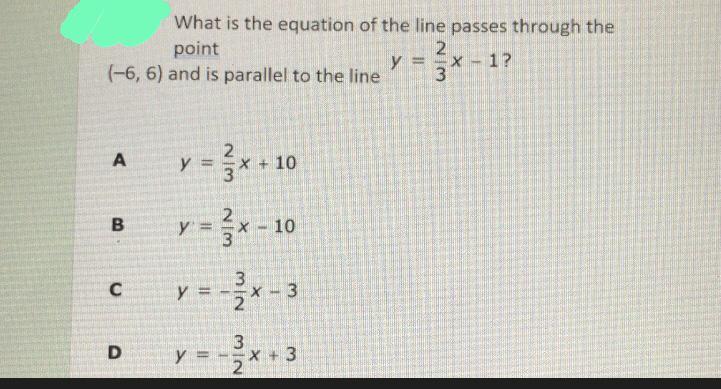
Answers
Answer: A
Step-by-step explanation:
The equation \(y=\frac{2}{3}x-1\) is in slope-intercept form(\(y=mx+b\)). For a line to be parallel to another, it must have the same slope. The slope of the line given is 2/3. Thus, simply plug in 2/3 for the slope to get: \(y=\frac{2}{3} x+b\). Then, because the line passes through -6, 6, plug those values in for x and y, respectively. \(6=\frac{2}{3} *-6+b\)
\(6=-4+b\)
\(10=b\)
Thus, the equation of the line is \(y = \frac{2}{3} x+10\), or A
Hope it helps :D
hello i am stuck at this question

Answers
If you turn off the spaceship's engine and it continues to glide in a straight line in the direction it was when the engine was stopped, we first have to find the speed of the spacecraft, which can be given by the formula:
V(t)= (dx/dt, dy/dt) V(t)= (1, 2t-2)How could we calculate t=1 and t=2?At t=1, the coordinates of the spaceship are (1,0). If we switch off the engine at this moment, the spaceship will continue to move in a straight line in the direction of its velocity vector, which is (1,0) at t=1.
At t=2, the coordinates of the spaceship are (2,1). If we switch off the engine at this moment, the spaceship will continue to move in a straight line in the direction of its velocity vector, which is (1,2) at t=2.
Therefore, at t=1 the spacecraft will move horizontally in a straight line. At t=2, the ship will move on a straight line with slope 2, passing through the point (2,1).
Find out more about velocity vector on:
https://brainly.com/question/626479
#SPJ1
the degenerative disease osteoarthritis most frequently affects weight-bearing joints such as the knee. an article presented the following summary data on stance duration (ms) for samples of both older and younger adults. age n sample mean sample sd older 28 801 117 younger 16 780 72 assume that both stance duration distributions are normal. a) calculate and interpret a 99% confidence interval (ci) for true average stance duration among elderly individuals. b) carry out a test of hypotheses to decide whether true average stance duration is larger among elderly individuals than among younger individuals. c) construct a 95% ci for the difference in means and compare results to part(b).
Answers
We are 99% confident that the true average stance duration among elderly individuals lies within the range of 744.56 ms to 857.44 ms.
To test whether the true average stance duration is larger among elderly individuals than among younger individuals, we can perform a one-tailed independent samples t-test. The null hypothesis (H0)
Using the t-test, we compare the means and standard deviations of the two samples and calculate the test statistic
a) To calculate a 99% confidence interval for the true average stance duration among elderly individuals, we can use the sample mean, sample standard deviation, and the t-distribution.
Given:
Older adults: n = 28, sample mean = 801, sample standard deviation = 117
Using the formula for a confidence interval for the mean, we have:
Margin of error = t * (sample standard deviation / √n)
Since the sample size is relatively large (n > 30), we can use the z-score instead of the t-score for a 99% confidence interval. The critical z-value for a 99% confidence level is approximately 2.576.
Calculating the margin of error:
Margin of error = 2.576 * (117 / √28) ≈ 56.44
The confidence interval is then calculated as:
Confidence interval = (sample mean - margin of error, sample mean + margin of error)
Confidence interval = (801 - 56.44, 801 + 56.44) ≈ (744.56, 857.44)
b) To test whether the true average stance duration is larger among elderly individuals than among younger individuals, we can perform a one-tailed independent samples t-test.
The null hypothesis (H0): The true average stance duration among elderly individuals is equal to or less than the true average stance duration among younger individuals.
The alternative hypothesis (Ha): The true average stance duration among elderly individuals is larger than the true average stance duration among younger individuals.
. With the given data, perform the t-test and obtain the p-value.
c) To construct a 95% confidence interval for the difference in means between older and younger adults, we can use the formula for the confidence interval of the difference in means.
Given:
Older adults: n1 = 28, sample mean1 = 801, sample standard deviation1 = 117
Younger adults: n2 = 16, sample mean2 = 780, sample standard deviation2 = 72
Calculating the standard error of the difference in means:
Standard error = √((s1^2 / n1) + (s2^2 / n2))
Standard error = √((117^2 / 28) + (72^2 / 16)) ≈ 33.89
Using the t-distribution and a 95% confidence level, the critical t-value (with degrees of freedom = n1 + n2 - 2) is approximately 2.048.
Calculating the margin of error:
Margin of error = t * standard error
Margin of error = 2.048 * 33.89 ≈ 69.29
The confidence interval is then calculated as:
Confidence interval = (mean1 - mean2 - margin of error, mean1 - mean2 + margin of error)
Confidence interval = (801 - 780 - 69.29, 801 - 780 + 69.29) ≈ (-48.29, 38.29)
Comparison with part (b): In part (b), we performed a one-tailed test to determine if the true average stance duration among elderly individuals is larger than among younger individuals. In part (c), the 95% confidence interval for the difference in means (-48.29, 38.29) includes zero. This suggests that we do not have sufficient evidence to conclude that the true average stance duration is significantly larger among elderly individuals compared to younger individuals at the 95% confidence level.
Know more about 99% confident here:
https://brainly.com/question/30762304
#SPJ11
Use the quadratic formula to solve the equation. If necessary, round to the nearest hundredth.
x² +3= -4x
O 1,3
O -1-3
O 1-3
O -1,3
Answers
Answer:
-1 -3
Step-by-step explanation:
Help plsssssssss I needed help

Answers
Answer:
Step-by-step explanation:
place a point at (0,0)- the starting point
next point at (2,1) - in 2 minutes she is 1 block away
Next point (4,2)- in 4 minutes she will be 2 blocks away
Connect those 3 points
then place a point at (9, 2)- 5 minutes later she was still at the store
Connect points
Point at (11,1) and (12,0) and connect
A total of 372 tickets were sold for the school play. They were either adult tickets or student tickets. The number of student tickets sold was two times the number of adult tickets sold. How many adult tickets were sold?
Answers
Answer:
248 tickets were students and 124 were adults! 372 ÷ 3 = 124 and 124 × 2 = 248 and 248 + 124 = 372 so
124 tickets for adults
and 284 tickets for students
After hearing his puppy yelp, for a moment after, Mr. Wright has a vivid auditory memory of the puppy's high pitch bark. Mr. Wright's experience clearly demonstrates ____________ memory.
Answers
"After hearing his puppy yelp, for a moment after, Mr. Wright has a vivid auditory memory of the puppy's high pitch bark. Mr. Wright's experience clearly demonstrates echoic memory."
Echoic memory is a form of sensory memory characterized by the temporary retention of auditory stimuli or sounds. It involves the capacity to retain and retrieve auditory information that has recently been perceived. As an example, Mr. Wright's strong recollection of the high-pitched bark of the puppy following its auditory encounter serves as evidence of his echoic memory. This suggests that the auditory details of the puppy's bark were briefly stored in his sensory memory, enabling him to mentally replay or recollect the sound within his mind for a short duration.
To put it differently, echoic memory pertains to the transient preservation of auditory input. It allows individuals to temporarily hold and recall auditory information that they have just heard. To illustrate, when Mr. Wright heard the puppy's shrill bark, he demonstrated his echoic memory by vividly recalling the sound afterward. This indicates that the sensory memory briefly encoded and stored the auditory aspects of the puppy's bark, granting Mr. Wright the ability to mentally replay or retrieve the sound within his consciousness for a brief period.
In summary, echoic memory represents a specific type of sensory memory that focuses on the brief retention of auditory stimuli. It enables individuals to remember and reproduce auditory information that has been recently perceived. In the case of Mr. Wright, his ability to vividly recall the puppy's high-pitched bark highlights his possession of echoic memory. This suggests that the auditory details of the bark were momentarily stored in his sensory memory, allowing him to mentally replay or remember the sound within his mind for a short period of time.
To know more about Information visit-
brainly.com/question/29102527
#SPJ11
Juli walks a path that is 1.6 miles long.
When he reaches the end of the trail, he turns around and goes back the same way. He stops to rest every 0.5 miles.
Which option explains how he can find how many times he stops to rest in total?
A.You have to divide 0.5 by 1.6.
B.She has to divide 1.6 by 0.5.
C.You have to multiply 1.6 by 2 and then divide the product by 0.5.
D.You have to multiply 1.6 by 2 and then multiply the product by 0.5.
(help)
Answers
Answer:
C
Step-by-step explanation:
Multiplying 1.6 gets you how far he walks, and then dividing the answer gives you how many times he would be stops, roughly 6.4 times
Evaluate the expression.
(65 + (1/5x 5) + 6) = 9
Answers
Let's verify
65+(1/5×5)+565+671As LHS not equal to RHS
This is not truePlease help me with the circled math question homework

Answers
The expressions are simplified to give;
7. 4n³(3n² + 4)
8. -3x(3x² - 4)
9. 5(k² - 8k + 2)
10. -10(6 + 6n² + 5n³)
11. 3(6n³ - 4n - 7)
12. 9(7n³ + 9n + 2)
What are algebraic expressions?Algebraic expressions are defined as mathematical expressions that are composed of variables, coefficients, terms, factors and constants.
These algebraic expressions are also made up of arithmetic operations, such as;
AdditionBracketSubtractionDivisionParenthesesMultiplicationTo factorize the expressions, we have;
12n⁵ + 16n³
Find the common term
4n³(3n² + 4)
-9x³ - 12x
find the common term
-3x(3x² - 4)
5k² - 40k + 10
find the common terms
5(k² - 8k + 2)
-60 + 60n² + 50n³
find the common term
-10(6 + 6n² + 5n³)
18n³ -12n - 21
find the common term
3(6n³ - 4n - 7)
63n³ + 81n + 18
Find the common term
9(7n³ + 9n + 2)
Learn about algebraic expressions at: https://brainly.com/question/4344214
#SPJ1