prove that:
cos20°cos40°cos80°=1/8
Answers
Answer:
see explanation
Step-by-step explanation:
Using the double angle identity for sine
sin2x = 2sinxcosx
Consider left side
cos20°cos40°cos80°
= \(\frac{1}{2sin20}\) (2sin20°cos20°)cos40°cos80°
= \(\frac{1}{4sin20}\) (2sin40°cos40°)cos80°
= \(\frac{1}{4sin20}\) (sin80°cos80° )
= \(\frac{1}{8sin20}\) (2sin80°cos80° )
= \(\frac{1}{8sin20}\) . sin160°
= \(\frac{1}{8sin20}\) . sin(180 - 20)°
= \(\frac{1}{8sin20}\) . sin20°
= \(\frac{1}{8}\) = right side , thus proven
Step-by-step explanation:
hope its helps you have a great day keep smiling be happy stay safe ☺

Related Questions
3. Morgan almost never writes checks anymore, but she recently used Check
301 to pay a $30 fee at her school and then sent Check 302 to her niece as a
$25 birthday gift. Have both checks cleared? If not, how much will come out
of her account soon for the missing check(s)?
Answers
If both checks have not cleared yet, $55 will come out of Morgan's account soon for the missing check(s).
To determine if both checks have cleared, we need to know the current status of Morgan's account. Without that information, we cannot definitively say whether the checks have cleared or not.
However, based on the information provided, we can calculate the total amount that will come out of Morgan's account soon for the missing check(s).
The total amount that will come out of Morgan's account soon can be calculated as the sum of the $30 fee and the $25 birthday gift, which is $55 in total.
Know more about Morgan's account here:
https://brainly.com/question/29195362
#SPJ11
HELP ASAPPPP
In two sample surveys, 125 people were asked about their favorite fruit. In the first survey, 40 people chose apples, 64 chose oranges, and 21 chose bananas. In the second, 43 chose apples, 63 chose oranges, and 19 chose bananas. Marianne inferred that most people prefer oranges. Is this inference true based on the data? Explain.
Answers
Answer:
More than half of the people surveyed in each sample chose oranges as their favorite fruit. Since most people in each sample chose oranges, it is likely that oranges are the favorite fruit of the entire population.
I hope this helps you
Step-by-step explanation:
A cone with a radius of 12 units and a height of 6 units
Answers

What is the Area of semicircle?
Answers
Step-by-step explanation:
Area of Semi Circle
The area of a semicircle is half of the area of the circle. As the area of a circle is πr2. So, the area of a semicircle is 1/2(πr2 ), where r is the radius.
Help really bad !!. I don’t understand for some reason

Answers
Answer:
x=-20
y=10
z=-19
Step-by-step explanation:
It is given that the shape is a rhombus, which means all four sides are equal. This means we can set up the equations:
5y-4=46 --> 5y=50 --> y=10
-2x+6=46 --> -2x=40 --> x=-20
-2z+8=46 --> -2z=38 --> z=-19
a quadrilateral with one right angle must be rectangle ?
Answers
Answer:
\(\Huge \boxed{\boxed{\textbf{False}}}\)
Step-by-step explanation:
A quadrilateral must have four right angles in order to be a rectangle, not simply one. A quadrilateral with a single right angle, however, can take on a wide range of shapes, like a right angled triangle or an irregular quadrilateral. A shape having multiple sides and one right angle, for example, could be an irregular quadrilateral.
Learn more about quadrilaterals.
↳https://brainly.com/question/32189100
#BTH1
________________________________________________________
Not good with factoring could use a hand.
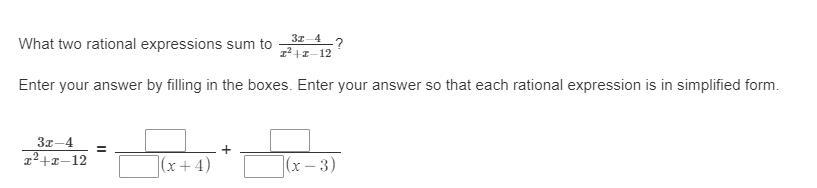
Answers
The only factoring you need to do is already done for you:
x² + x - 12 = (x + 4) (x - 3)
What you're asked to do is decompose
(3x - 4) / (x² + x - 12)
into partial fractions, i.e. find a and b such that
(3x - 4) / (x² + x - 12) = a / (x + 4) + b / (x - 3)
Multiply both sides by x² + x - 12 :
3x - 4 = a (x - 3) + b (x + 4)
3x - 4 = (a + b) x + (-3a + 4b)
So we have
a + b = 3
-3a + 4b = -4
and solving this system gives
a = 16/7 and b = 5/7
so you should submit the numbers in bold:
(3x - 4) / (x² + x - 12) = 16 / (7 (x + 4)) + 5 / (7 (x - 3))
For each expression, write an equivalent expression that uses only addition. 4x−7y−5z+6
Answers
Answer:
Step-by-step explanation:
x + x + x + x - y - y - y - y - y - y - y - z - z - z - z - z + 1 + 1 + 1 + 1 + 1 + 1
The table shows different quantities of flour and the number of cookies that can be made with each quantity of flour. If the relationship between the cups of flour and the number of cookies is proportional, find the value of x.
Flour(cups)=3-6-12
cookies=4-x-16
(dozens)
Answers
8 is the right answer and the right value of X.
What are patterns in math's?
In mathematics, a pattern is a recurrent arrangement of numbers, forms, colors, and other elements. Any event or object can be related to the Pattern. An arrangement of numbers is referred to as a pattern when it is done in a certain way. Sometimes a pattern is referred to as a series.
What are different types of pattern in math's?
Arithmetic Sequence is one of them.Geometric Order.Square figures.Number Cubes.Triangle-shaped numbersa Fibonacci sequenceSo,
3 cups of flour = 4 dozen cookies
using twice as much flour (6 cups) will result in 8 dozen cookies.
To know more about about patterns and series, visit:https://brainly.com/question/7043766
#SPJ4
which angles are coterminal with an angle measure of 2pi/3
Answers
The resulting angle of 4 π / 3 is positive and coterminal with - 2π / 3
What are coterminal angles ?
Coterminal angles are the angles that have the identical initial facet and share the terminal aspects. these angles occupy the usual function, though their values are one of a kind. they are at the same sides, within the identical quadrant and their vertices are same. while the angles are moved clockwise or anticlockwise the terminal aspects coincide at the identical attitude.
Given angles measure of -2 pi / 3
So we have to add 2π to - 2 π / 3
- 2π / 3 + 2 π
= 2π - 2π / 3
= 6 π - 2 π / 3
= 4π / 3
The resulting angle of 4 π / 3 is positive and coterminal with - 2π / 3
Therefore, The resulting angle of 4 π / 3 is positive and coterminal with
- 2π / 3
To learn more about Coterminal angles from given link.
https://brainly.com/question/29133154
#SPJ1
I neeeeeeeeeeeeeed HELP

Answers
Answer:
A.) CPCTC (Please mark Brainliest)
Step-by-step explanation:
First triangle is proven congruent then parts are said to be congruent
Sally deposits $1,600 into a savings account earning a simple interest rate of 7.00%. How much interest will she earn after 180 days? Express your answer to 2 decimal places.
Answers
Sally deposits $1,600 into a savings account earning a simple interest rate of 7.00%., then the interest Sally will earn after 180 days is $55.09.
To calculate the amount of interest Sally will earn after 180 days on depositing $1600 in a savings account with a simple interest rate of 7%, the following formula applies;Interest = P × r × t
where;P is the principal (amount deposited),r is the annual interest rate (7%),t is the time in years or fraction of a year.
We can convert 180 days to fraction of a year by dividing it by the total number of days in a year as follows;
180 days ÷ 365 days = 0.49315068 years
Substitute the values of P, r and t to calculate the interest;
Interest = 1600 × 0.07 × 0.49315068
Interest = 55.09
To two decimal places, the interest Sally will earn after 180 days is $55.09.
Learn more about interest rates at
https://brainly.com/question/2437603
#SPJ11
A police car is approaching a right-angled intersection from the north at 35 mph, and a speeding car is heading east at 30 mph. When the police car is 0.75 miles north of the intersection and the speeding car is 1 mile to the east, what is the rate that the distance between the police car and car is changing?
Answers
Answer:
The rate that the distance between the police car and car is changing = 3 m/s
Step-by-step explanation:
The given speed of the police car = 35 mph
The speed of the speeding car = 30 mph
The position of the police car = 0.75 miles north
The position of the speeding car = 1 miles east
The distance of the police car from the speeding car, d = √(0.75² + 1²) = 1.25
d² = x² + y²
2d·dd/dt = 2x·dx/dt + 2·y·dy/dt
Where;
dx/dt = 30 mph
dy/dt = -35 mph
x = 1
y = 0.75
Substituting gives;
2×1.25 ×dd/dt = 2×1×30 - 2×0.75×35
2×1.25 ×dd/dt = 7.5
dd/dt = 7.5/2.5 = 3
dd/dt = 3 m/s
The rate that the distance between the police car and car is changing = dd/dt = 3 m/s
Answer:
The answer is increasing by 3 mph
Step-by-step explanation:
Given that AB:BC is 4:3 and AC = 56. Find AB.
A
B
Answers
Answer:
ab=32
Step-by-step explanation:
ab:bc
4:3
abc= 56
4+3=7
56÷7=8
ab= 8x4=32
bc=8x3=24 #
laura compro un microondas por 216.750 y una lavadora 910.350 si le rebajaron 43.350 en la compra y el resto la paga en 15 plazos ¿cuanto paga en cada plazo?
Answers
A right triangle is shown below with the dimensions given in units.
Which measurement is closest to the value of y in units?
A right triangle is shown below with the dimensions given in units.
Which measurement is closest to the value of y in units?

Answers
The value of y in the right triangle is 9.3 units.
How to find the side of a right triangle?A right triangle is a triangle that has one of its angles as 90 degrees. The sum of angles in a triangle is 180 degrees.
Therefore, let's find the value of y in the right angle triangle.
Using trigonometric ratios,
sin 51 = opposite / hypotenuse
sin 51 = y / 12
cross multiply
12 sin 51 =y
y = 12 × 0.77714596145
y = 9.32575153748
y = 9.3 units
learn more on right triangle here: brainly.com/question/28975129
#SPJ1
What is the base if the rate is 16.3% and the portion is 457?
Answers
Solution
Step 1
Rate = (Portion/Base)*100%
Step 2
Rate = 16.3
Portion B = 4557
Let x reoresent the early
\(\begin{gathered} 16.3\text{ = }\frac{457}{x}\text{ }\times100 \\ \\ x\text{ = }\frac{457}{16.3}\text{ }\times\text{ 100\%} \\ \\ x\text{ = 2804} \\ \end{gathered}\)
Which of the following choices will simplify (8 − 5)2 + + 4
Answers
Answer:
10
Step-by-step explanation:
(8-5)2 + 4, let's start with the first step, the parentheses.
(8-5)=3 , then we multiply by 2, so (3)*2 which equals 6. 6+4=10!
Hope this helps! :)
Answer: the answer is 19
Step-by-step explanation:
i just got this question and got it right!
What is the value of the expression below when z=6z=6 and w=7w=7?
8z+7w
Answers
8z + 7w; z = 6; w = 7
8z + 7w
=(8x6) + (7x7)
=48 + 49
=97
The answer is 97.
Answer:
97
Step-by-step explanation:
BIG BRAIN
Describe in detail the Dickey-Fuller and the augumented Dickey-Fuller (ADF) procedure for testing for the
order of integration of a time series variable.
Answers
The Dickey-Fuller test is a statistical test used to determine the presence of a unit root in a time series variable, which indicates the degree of integration of the variable. The null hypothesis of the test is that the variable has a unit root and is non-stationary.
The Dickey-Fuller test calculates a t-statistic based on the coefficient estimate of an autoregressive lagged term in a regression model. If the calculated t-statistic is less than the critical value, the null hypothesis is rejected, indicating that the variable is stationary and does not have a unit root. The augmented Dickey-Fuller (ADF) test extends the Dickey-Fuller test by including additional lagged terms in the regression model. The purpose of adding lagged terms is to capture any potential serial correlation and provide more accurate results. The ADF test allows for testing multiple lags and selecting the appropriate lag length using information criteria such as the Akaike Information Criterion (AIC) or the Schwarz Information Criterion (SIC). By including more lags, the ADF test improves the reliability of the test and provides more robust results. In summary, both the Dickey-Fuller and augmented Dickey-Fuller procedures are used to test for the order of integration of a time series variable. They examine whether the variable exhibits a unit root, indicating non-stationarity. The ADF test, with its inclusion of additional lagged terms, enhances the reliability of the test and allows for the selection of the optimal lag length.
Learn more about the Dickey-Fuller here: brainly.com/question/33545080
#SPJ11
A bouncy ball is dropped such that the height of its first bounce is 3.25 feet and each successive bounce is 74% of the previous bounce's height. Write a recursive formula to represent the height of the nth bounce of the ball.
Answers
A recursive formula to represent the height of the nth bounce of the ball is: aₙ = 3.25(0.74ⁿ ⁻ ¹)
How to write a recursive formula?A geometric sequence is a sequence in which the result of the division of consecutive terms is always the same, called common ratio q.
The nth term of a geometric sequence is given by:
aₙ = a(qⁿ⁻¹)
where:
a is the first term
In this problem, the first bounce is 3.25 feet and each successive bounce is 74% of the previous bounce's height, hence the first term and the common ratio are given, respectively, by:
a = 3.25
q = 74% = 0.74
Hence, the height of the nth bounce is given by:
aₙ = 3.25(0.74ⁿ ⁻ ¹)
Read more about Recursive Formula at: https://brainly.com/question/1275192
#SPJ1
gina wilson all things algebra geometry unit 4 homework 3.

Answers
Answer:
9. The answer is 208
10. The anwer is 122°
11. m∠1 = 43°
m∠2 = 17°
m∠3 = 120°
m∠4 = 60°
m∠5 = 60°
m∠6 = 60°
m∠7 = 17°
m∠8 = 120°
m∠9 = 43°
Step-by-step explanation:
Long explanation that's why I don't have to put it. But I solved it on a scratch paper so you don't have to doubt me. I hope it helps
9.each side of the equilateral triangle has a length of 190 units.
10.The angles of the triangle are approximately: Angle 1 = 29 degrees
Angle 2 ≈ 10.5 degrees and Angle 3 = 11x - 65 ≈ 139.7273 degrees
11. m∠1 = 43° , m∠2 = 17° , m∠3 = 120° , m∠4 = 60° , m∠5 = 60°, m∠6 = 60°
9.Given that two angles in a triangle are 60 degrees each, we have an equilateral triangle, where all three angles are equal to 60 degrees.
In an equilateral triangle, all three sides are also equal. Let's denote the length of each side as "s."
You are given two expressions for the sides: 1. First side: 7x + 19 2. Second side: 11x - 89
Since the triangle is equilateral, all three sides have the same length. Therefore, we can set up the following equation:
7x + 19 = 11x - 89
Now, solve for "x":
Subtract 7x from both sides: 19 = 4x - 89
Add 89 to both sides: 108 = 4x
Divide by 4: x = 27
Now that we have the value of "x," we can substitute it back into either of the expressions to find the length of each side. Let's use the first expression: First side = 7x + 19 = 7 * 27 + 19 = 190
So, each side of the equilateral triangle has a length of 190 units.
10. In a triangle, the sum of all three angles is always 180 degrees. Therefore, to find the value of the second angle when one angle is 29 degrees and the third angle is expressed as 11x - 65 degrees, we can set up the following equation:
Angle 1 + Angle 2 + Angle 3 = 180
Given: Angle 1 = 29 degrees, Angle 3 = 11x - 65 degrees
Let's denote Angle 2 as "A2": 29 + A2 + (11x - 65) = 180
Simplify the equation: A2 + 11x - 36 = 180
Now, you mentioned that Angle 2 is expressed as 11x - 65 degrees. So, we can equate this expression to "A2": 11x - 65 = A2
Substitute this expression for A2 back into the equation: 11x - 65 + 11x - 36 = 180
Combine like terms: 22x - 101 = 180
Add 101 to both sides: 22x = 281
Divide by 22: x = 281 / 22 ≈ 12.7727
Now that we have the value of "x," we can find Angle 2 using the expression 11x - 65: Angle 2 = 11x - 65 = 11 * 12.7727 - 65 ≈ 10.5 degrees
So, the angles of the triangle are approximately:
Angle 1 = 29 degrees
Angle 2 ≈ 10.5 degrees
Angle 3 = 11x - 65 ≈ 139.7273 degrees
11.m∠7 = 17° , m∠8 = 120° ,m∠9 = 43°
To know more about triangle:
https://brainly.com/question/25813512
#SPJ3
What is the value of x? Do not round your answer.

Answers
Answer:
x = 3
Step-by-step explanation:
Setup a proportion
\(\frac{CB}{CA} =\frac{DB}{DA} \\\frac{4}{3} =\frac{x}{2.25} \\3x=9\\\frac{3x}{3} =\frac{9}{3} \\x=3\)
Two buses are 515 miles apart. At 9:30 A.M. they start traveling toward each other at rates of 48 and 55 miles per hour. At what time will they pass each other
Answers
The two buses are initially 515 miles apart and are moving toward each other. They will pass each other around 2:30 P.M.
To solve this problem, we can use the concept of relative speed. The combined speed of the two buses is the sum of their individual speeds, which is 48 + 55 = 103 miles per hour.
We can calculate the time it takes for the buses to meet by dividing the initial distance between them (515 miles) by their combined speed (103 miles per hour):
Time = Distance / Speed
Time = 515 miles / 103 miles per hour
Time ≈ 5 hours
Therefore, the two buses will pass each other approximately 5 hours after they start traveling toward each other. To determine the exact time, we need to consider the starting time (9:30 A.M.) and add 5 hours to it. So, they will pass each other around 2:30 P.M.
Learn more about miles per hour here:
https://brainly.com/question/31684642
#SPJ11
Whats the answer to this operation?

Answers
Answer: 18x^2 + 9x - 5
Step-by-step explanation:
19/23 as a decimal rounded to the nearest tenth
i need the answer for aleks
Answers
Answer:
0.8
Step-by-step explanation:we just need to divided 19 by 23
and rounded to the nearest tenth it’s .8
Hopes this helps please mark brainliest
A scale drawing of a famous statue uses a scale factor of 220:1. If the height of the drawing is 1.2 feet, what is the actual height of the statue?
264 feet
221.2 feet
218.8 feet
183.3 feet
Answers
Answer:
264
Step-by-step explanation:
Set a proportion:
220 : 1 = x = 1.2
x = (220×1.2)÷1 = 264
Answer:
To find the actual height of the statue, we need to use the scale factor to convert the height of the drawing to the actual height of the statue:
actual height = drawing height × scale factor
actual height = 1.2 feet × 220
actual height = 264 feet
Therefore, the actual height of the statue is 264 feet. Answer: A) 264 feet.
A company with 17 employees gives each employee a bonus of $459. How much does the company spend on bonuses?
O $27
O $476
O $4,590
O $7,803
Answers
Answer: Option D: $7803
Step-by-step explanation:
just multiply 459 by 17 and you get your answer.
A medium water hose can fill a pool in 30 mins. A larger water hose can fill a pool in 20 mins. If both hoses are turned on at the same time, how long will it take to fill the pool? Drag each tile to the correct cell in the table. QUICK PLEASE!

Answers
Answer:
25 mins
Step-by-step explanation:
add both then divide by 2
you have started your position as transportation director in a small town called mountainside village. there is only one road in and out of town. today you can expect at peak traffic to see 35 cars per hour and the drive along the road with no traffic is 1 minute. assuming poisson arrival and exponential drive times, what is the current utilization of the road? (4 points)
Answers
The current utilization of the road is 0.5833 or 58.33%. To calculate the current utilization of the road, we need to use the formula:
Utilization = Arrival rate x Drive time
Since we are assuming Poisson arrival and exponential drive times, we can use the following formulas:
Arrival rate = λ = 35 cars per hour
Drive time = 1/μ = 1/60 hours (since the drive time is 1 minute)
Therefore,
Utilization = 35 cars per hour x (1/60 hours)
Utilization = 0.5833 or 58.33%
So the current utilization of the road in Mountainside Village is 58.33%.
Hi! As the transportation director of Mountainside Village, we can calculate the current utilization of the road using the given terms. The peak traffic rate is 35 cars per hour, and the drive time without traffic is 1 minute (or 1/60 hours).
Since we're assuming Poisson arrival and exponential drive times, we can calculate the utilization (ρ) using the formula:
ρ = λ / μ
Here, λ represents the arrival rate (35 cars/hour), and μ represents the service rate, which is the inverse of the average drive time (1/60 hours).
So, μ = 1 / (1/60) = 60 cars/hour
Now, we can calculate the utilization:
ρ = 35 cars/hour / 60 cars/hour = 0.5833 (rounded to 4 decimal places)
Thus, the current utilization of the road is 0.5833 or 58.33%.
Visit here to learn more about exponential brainly.com/question/28596571
#SPJ11