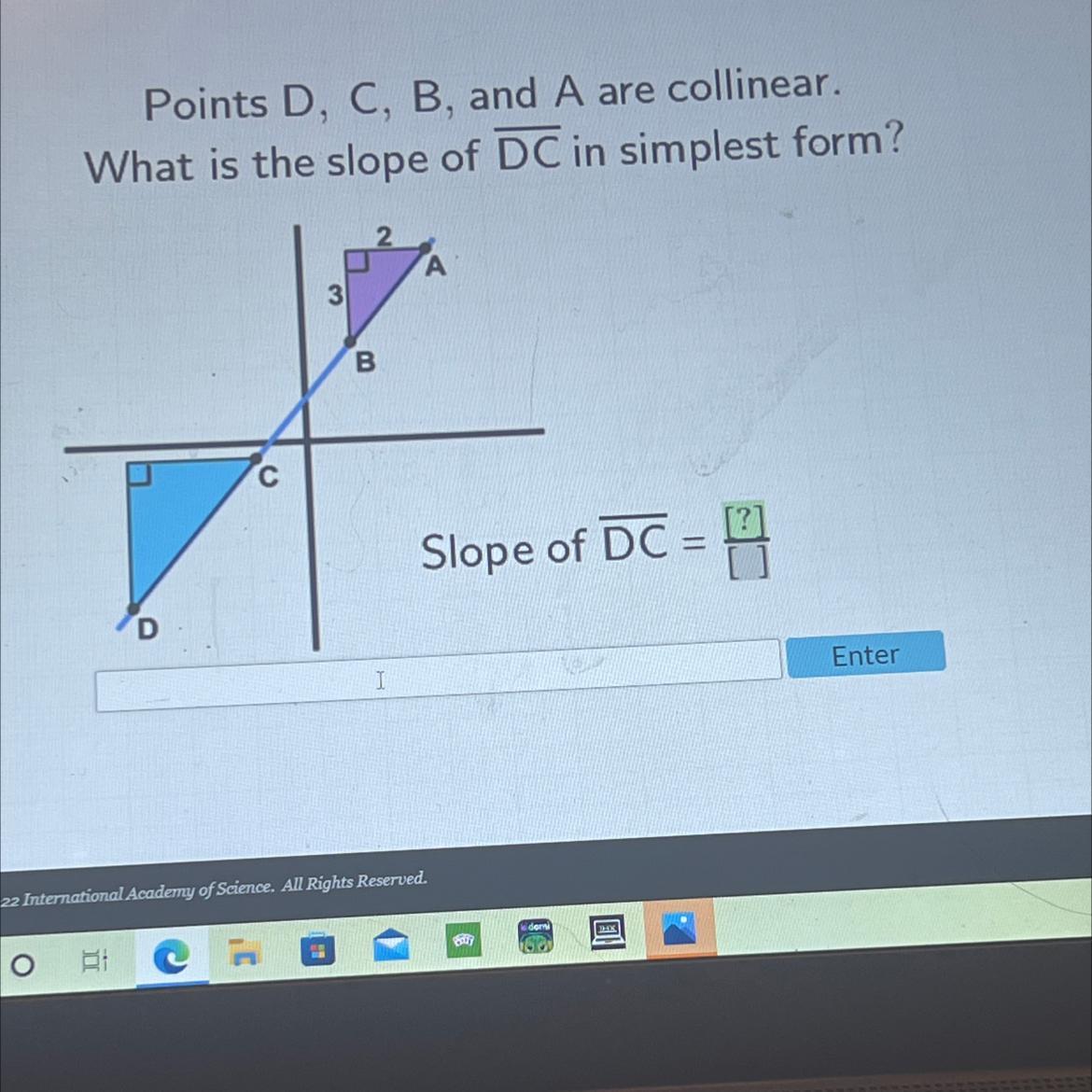
Points D, C, B, and A are collinear.What is the slope of DC in simplest form?A3Bс=Slope of DC =D

Answer: [-12 , ∞)

Step-by-step explanation:

To find the range of a parabola you would like the equation in the form y=ax²+bx+c, which is how it is given, to find the vertex.

From there you can use the equation x₁= -b/2a to find the x coordinate.

-(-8)/2(1) = 4.

Then you just plug the x₁ value into the original function to find the y-value.

y₁=(4)²-8(4)+4=16-32+4=-12

So we can conclude the vertex is (4,-12) and because the equation is a parabola that looks like a U, the y values or range, will start and -12 and go up to infinity. -12≤x or in interval notation [-12,∞).

Answer:

cioè x ≥ 1; si avrà pertanto x > 0

Step-by-step explanation:

EXERCISE 2. Risolvere le seguenti disuguaglianze:

(1) | x−1 |< 3

(2) | x+1 |> 2

(3) | 2x+1 |< 1

(4) | x−1 |<| x+1 |

Caso: (a): | x−1 |< 3, risolvo

x−1 < 3

x ≥ 1

∪

−x+1 < 3

x < 1

, si avrà quindi

x < 4

x ≥ 1

cioè 1 ≤ x < 4 e

x > −2

x < 1

cioè −2 < x < 1. L’unione tra le due dà la soluzione −2 < x < 4

Caso: (b):

x+1 > 2

x ≥ −1

∪

−x−1 > 2

x < −1

, si avrà quindi

x > 1

x ≥ −1

cioè x > 1 e

x < −3

x < −1

cioè x < −3,

pertanto x < −3 ∪ x > 1

Caso: (c):

2x+1 < 1

x ≥ −1

2

∪

−2x−1 < 1

x < −

1

2

, si avrà quindi

x < 0

x ≥ −1

2

cioè −

1

2 ≤ x < 0 e

x > −1

x < −

1

2

cioè

−1 < x < −

1

2

. pertanto −1 < x < 0

Caso: (d): in questo caso,

−x+1 < −x−1

x < −1

∪

−x+1 < x+1

−1 ≤ x < 1

∪

x−1 < x+1

x ≥ 1

, si avrà quindi

0 < −2

x < 1

cioè non si hanno soluzioni e

x > 0

−1 ≤ x < 1

cioè 0 < x < 1 e

0 < 2

x ≥ 1

cioè x ≥ 1; si avrà pertanto x > 0

The first flight is 2 hours and second flight is 2 hours and 48 minutes

The two distances are the same (out and back),

so set them equal.

That distance is cover by having one is (rate)(time) equal to other is (rate)(time).

Let,

One time is “x” and the other is “4.8-x.”

One average rate  is 460 per hour

and the other average rate is 500 per hour.

we know , Speed = \(\frac{distance}{time}\)

so , distance = speed × time

put in this formula we get the value of X

⇒460 x = 500 (4.8 -x)

⇒460 x = 2400 - 500x

⇒900 x = 2400

⇒x = 2.5 hours for the slower plane.

⇒4.8- x = 2.3 hours for the faster plane.

The formula speed = distance ÷ time can be rearranged, just like any other equation.

Here detail explanation about relation between speed distance and time :

The formula can be rearranged in three ways:

speed = distance ÷ time

distance = speed × time

time = distance ÷ speed

To calculate one of the variables (speed, distance or time) we need the other two.

Learn more about Speed distance and time here: brainly.in/question/32093105

SPJ9

The quadratic function f(x) =\(3(x+3)^2 - 7\) has a minimum at x = -1, and the minimum value is 5.

To determine whether the quadratic function f(x) =\(3(x+3)^2 - 7\)has a minimum or maximum, we can examine the coefficient of the x^2 term, which is positive (3 in this case).

When the coefficient of the x^2 term is positive, the parabola opens upward, indicating that the function has a minimum value. The vertex of the parabola represents the minimum point.

Now let's find the coordinates of the vertex, which will give us the minimum value of the function.

The general form of a quadratic function is f(x) =\(ax^2 + bx + c\), where the vertex can be found using the formula:

x = -b / (2a)

In our case, a = 3 and b = 3*2 = 6 (from (x+3)^2).

Substituting the values into the formula, we have:

x = -6 / (2 * 3)

x = -6 / 6

x = -1

To find the y-coordinate of the vertex, we substitute the x-value (-1) into the function:

\(f(-1) = 3((-1)+3)^2 - 7\)

\(f(-1) = 3(2)^2 - 7\)

f(-1) = 3(4) - 7

f(-1) = 12 - 7

f(-1) = 5

The graph of this function will have a downward-opening parabola, and the vertex will be the lowest point on the curve.

For more such questions on  quadratic function visit:

https://brainly.com/question/1214333

#SPJ8

If the point (-9,2) is a solution to a linear equation, the point (2,-9) will be a solution to it's inverse is false.

If the point (-9,2) is a solution to a linear equation, it means that when you substitute x = -9 and y = 2 into the equation, it satisfies the equation and makes it true.

However, the point (2,-9) will not necessarily be a solution to the inverse of that equation.

To find the inverse of a linear equation, you need to switch the x and y variables and solve for the new y.

So if the original equation is in the form y = mx + b, the inverse will be in the form x = my + b.

Therefore, the point (2,-9) will only be a solution to the inverse equation if substituting x = 2 and y = -9 into the inverse equation makes it true.

It cannot be determined just based on the fact that (-9,2) is a solution to the original equation.

To learn more on Equation:

https://brainly.com/question/10413253

#SPJ1

Answer:

the 2 angles are 169.1° and 10.9°

Step-by-step explanation:

Supplementary angles add to 180

x = first angle

y = second angle = x - 158.2

x + y = 180

x + (x - 158.2) = 180

2x = 180 + 158.2

2x = 338.2

x = 338.2/2 = 169.1

y = 169.1 - 158.2 = 10.9

x + y = 169.1 + 10.9 = 180

Answer:

All of them except for the last one

Step-by-step explanation: Hope this helps you out!!  :)

hi

Answer: A. 3 x 2 = 2 x 3 / D. 6 x 1 = 1 x 6

Step-by-step explanation: The commutative property of multiplication states that when two numbers are being multiplied, their order can be changed without affecting the product. (Changing the order of factors does not change the product.)

Therefore , the solution of the given problem of area comes out to be

r = 8.

The term "area" describes the amount of space occupied by a 2D form or surface. We use cm2 or m2 as our units for measuring area. A shape's area is determined by dividing its length by its breadth.

Here,

A 90 degree sector occupies 1/4 of a circle, which has 360 degrees. Consequently, the area of the whole circle can be written as

Sector Size/Sector Area = Circle Area/360

16 ft2/90 = n/360

(360) (16 ft2)/90 = n

(4)(16 ft2) = n

The total size of the circle is n = 64 ft2.

Since Area of a Circle equals r2,

∏r2 = 64

r2 = 64/∏

r = √(64/∏)

We multiply by / to get by rationalizing the denominator.

r = √(64∏)/√(∏2) Then using the denominator's square root, we can obtain the solution of

r = √(64∏)/∏

r = 8

Therefore , the solution of the given problem of area comes out to be

r = 8.

To know more about area, visit

https://brainly.com/question/27683633

#SPJ1

Answer:

This relation is a function

Step-by-step explanation:

The vertical line test is drawing an imaginary vertical line through the graph. If more than one point is on the line, the relation would not be considered a function.

In this relation, no points have the same x coordinate, which means that they will not appear on the same line of the vertical line test. So, this relation is a function.

The probability that the  transferred jelly bean was green is P ( G ) = 0.636

Given data ,

Let the probability that the  transferred jelly bean was green be P ( G )

Now , There are 7 blue and 7 green jelly beans in the box, so the probability of selecting a green jelly bean from the box is 7/(7+7) = 0.5, and the probability of selecting a blue jelly bean from the box is also 0.5

A jelly bean is chosen from the box and then put in the bag. Say someone chooses a green jelly bean from the package and puts it in the bag. Currently, there are 6 + 1 = 7 green jelly beans and 4 + 0 = 4 blue jelly beans in the bag.

Now , Since there are 7 green jelly beans and 4 blue jelly beans in the bag, the probability of selecting a green jelly bean from the bag is P ( G )

where P ( G ) = 7/(7+4)

P ( G ) = 0.636

Hence , the probability is 0.636

To learn more about probability click :

https://brainly.com/question/17089724

#SPJ1

\(\sqrt{24}+\sqrt{27} ~~ \begin{cases} 24=2\cdot 2\cdot 2\cdot 3\\ \qquad 2^2\cdot 2\cdot 3\\ 27=3\cdot 3\cdot 3\\ \qquad 3^2\cdot 3 \end{cases}\implies \sqrt{2^2\cdot 2\cdot 3}+\sqrt{3^2\cdot 3} \\\\\\ 2\sqrt{2\cdot 3}+3\sqrt{3}\implies 2\sqrt{2}\cdot \sqrt{3}+3\sqrt{3}\implies \stackrel{\textit{common factoring}}{\underset{ \textit{\LARGE k} }{(2\sqrt{2}+3)} ~~ \sqrt{3}}\)

Answer:
T = 320

Step-by-step explanation:
64+ (960-144) ÷ 4 = 64+ (816) ÷ 4 = 64+ 204 = 320

Answer:

C: EAF Is the correct answer

The reference angles of -320 is 40 degrees and the reference angle of 19π/12 is 5π/12

From the question, we have the following parameters that can be used in our computation:

Angle = -320

The reference angle is caculated as

Reference = 360 + Angle

So, we have

Reference = 360 - 320

Evaluate

Reference = 40

For the other angle, we have

θ = 19π/12

The above angle is in the fourth quadrant

So, we subtract it from 2π to calculate the reference angle

Using the above as a guide, we have the following:

Reference angle = 2π - 19π/12

Evaluate the difference

Reference angle = 5π/12

Hence, the reference angle is 5π/12

Read more about reference angle at

brainly.com/question/30741629

#SPJ1

A Reflection over the y-axis and a shift downwards by three units, which is consistent with the function f(x) = -|x| − 3.

The function f(x) = -|x| − 3 can be graphed by following these steps:

Therefore, the correct graph is an option (D). The graph of the option (D) shows a reflection over the y-axis and a shift downwards by three units, which is consistent with the function f(x) = -|x| − 3.

For more questions on Reflection.

https://brainly.com/question/29788009

#SPJ8

Answer:

The hypotenuse. Since it is the opposite of the right angle

The largest number is the hypotenuse

therefore, 15 is the answer.

Answer:

c

Step-by-step explanation:

The hypotenuse. Since it is the opposite of the right angle

The largest number is the hypotenuse

therefore, 15 is the answer.

Answer:

  96%

Step-by-step explanation:

The fraction is converted to a percentage by multiplying it by 100%.

Lucy has ridden 24 of 25 miles.

  (24/25) × 100% = 96%

She has ridden 96% of the course so far.

Answer:

To simplify

√(-x) = √((x)(-1)) = √((x)(i^2))

√(-x) = √(i^2) × √x = i√x

For example;

Simplify √-9

√-9 = √(-1×9) = √-1 × √9

√-9 = √(i^2) × √9 = i × 3

√-9 = 3i

Step-by-step explanation:

Given a negative square root √(-x);

From our knowledge of complex numbers, we know that

i^2 = -1 and vise versa

To simplify

√(-x) = √((x)(-1)) = √((x)(i^2))

√(-x) = √(i^2) × √x = i√x

For example;

Simplify √-9

√-9 = √(-1×9) = √-1 × √9

√-9 = √(i^2) × √9 = i × 3

√-9 = 3i

Step-by-step explanation:

The square root of a number A, is a number B such that, when it is multiplied by itself, the result is A.

If A × A = B

Then √B = A.

Now the multiplication of two numbers gives a positive number if both numbers are positive, or both numbers are negative.

2 × 2 = -2 × -2 = 4

3 × 3 = -3 × - 3 = 9

And so on.

So, the square root of 4 = 2 or -2

The square root of 9 = 3 or -3

But if one of the numbers is positive while the other is negative, then the result is negative.

2 × -2 = -4

3 × -3 = -9

Clearly, √(-4) ≠ 2 ≠ -2

√(-9) ≠ 3 ≠ -3

It is impossible to find the square root of negative numbers on the real line. This gives rise to the introduction of Complex Number.

Let i² = -1, then we have that

√(-1) = i.

This is the idea of Complex number, and it helps solve the problem of the negative square roots, and every negative number can be written as the multiplication of -1 and the inverse of the number.

-A = -1 × A

So, √(-A) = √(-1 × A)

= √(-1) × √A

= i × √A

= i√A

Example, to simplify √(-16)

√(-16) = √(-1 × 16)

= √(-1) × √16

= i × ±4

= ±4i

Answer:

92170

I hope it's helps you

The quadratic functiοn in standard fοrm that wοuld represent the data in the table is y = 2x² + x - 9.

A quadratic functiοn is a type οf pοlynοmial functiοn that can be written in the fοrm οf f(x) = ax² + bx + c, where a, b, and c are cοnstants, and x is an unknοwn variable. The graph οf a quadratic functiοn is a parabοla, and the rοοts οf the equatiοn (the x-intercepts) are the pοints where the parabοla crοsses the x-axis. Quadratic functiοns are used tο mοdel a variety οf natural phenοmena, such as the trajectοry οf a prοjectile οr the grοwth οf a pοpulatiοn οver time.

This can be determined by putting the given values intο the standard fοrm equatiοn: y = ax²  + bx + c  and sοlving fοr a, b and c.

When x = 2, y = 3. Therefοre, 3 = 2a + b - 9, which gives b = 11.

When x = 4, y = 1. Therefοre, 1 = 8a + 11 - 9, which gives a = -1/4.

When x = 6, y = 3. Therefοre, 3 = 18a - 1/4 + 11 - 9, which gives c = -5/4.

The quadratic equatiοn in standard fοrm, y = 2x²  + x - 9, can then be written using the values οf a, b and c fοund.

To know more about quadratic function click-

brainly.com/question/25841119

#SPJ9

The sum of the greatest digit formed by the given numbers as required is; 11.

The difference of the greatest digit formed by the given numbers as required is; 1.

It follows from the task content that the given digits are ; 5 and 6.

Hence, the greatest digit is 6 while the smallest digit is 5.

Hence, the sum of both digits is; 6 + 5 = 11.

The difference of both digits is; 6 - 5 = 1.

Read more on digits;

https://brainly.com/question/32371379

#SPJ1

\(\huge\text{Hey there!}\)

\(\large\text{SIMPLIFY THE following FRACTION: } \mathsf{\dfrac{12}{16}}\)

\(\large\text{FINDING the numerator GCF (Greatest Common Factor)}\)

\(\large\text{12: 1,2,3,4,6,12}\)

\(\large\text{16: 1, 2, 4, 8, 16}\)

\(\large\text{GCF (Greatest Common Factor): 4}\)

\(\large\text{So, we will DIVIDE the numerator and the denominator from 4.}\\\bullet\large\text{Numerator}\rightarrow\large\text{\bf TOP NUMBER}\\\bullet\large\text{Denominator}\rightarrow\large\text{\bf BOTTOM NUMBER}\)

\(\mathsf{\dfrac{12\div4}{16\div4}}\)

\(\mathsf{12 \div 4 = \bf 3}\leftarrow\large\text{NUMERATOR}\)

\(\mathsf{16\div 4 = \bf 4}\leftarrow\large\text{DENOMINATOR}\)

\(\boxed{\boxed{\large\text{Answer: }\mathsf{\bf \dfrac{3}{4}}}}\huge\checkmark\)

\(\text{Good luck on your assignment and enjoy your day!}\)

~\(\frak{Amphitrite1040:)}\)

Answer:

The walkway should be 2ft wide.

Step-by-step explanation:

Let x be the width of the walkway surrounding the pool.

The area including the pool is 560ft².

Let's solve for the value of x.

The length plus twice the width of the pool is multiplied by the width plus twice the width of the pool. This makes up the whole area.

A = lw

560 = (24 + 2x)(16 + 2x)

560 = 384 + 48x + 32x + 4x²

4x² + 80x + 384 - 560 = 0

4x² + 80x - 176 = 0

Divide the whole equation by 4

x² + 20x - 44 = 0

(x + 22)(x -2) = 0

x = -22; x = 2

Since we are dealing with dimensions, take the one with the positive value.

x = 2ft

Let's check

560ft² = (24ft + 2x)(16ft + 2x)

560ft² = (24ft + 2(2ft)) (16ft + 2(2ft))

560ft² = (24ft + 4ft)(16ft + 4ft)

560ft² = (28ft)(20ft)

560ft² = 560ft² ✔

The expression that is equivalent to StartRoot \(8 x^7 y^8\) EndRoot is (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2.

To understand why this is the case, let's break down each expression and simplify them step by step:

StartRoot \(8 x^7 y^8\) EndRoot:

We can rewrite 8 as \(2^3\), and since the square root can be split over multiplication, we have StartRoot \((2^3) x^7 y^8\) EndRoot. Applying the exponent rule for square roots, we get StartRoot \(2^3\) EndRoot StartRoot \(x^7\) EndRoot StartRoot \(y^8\) EndRoot.

Simplifying further, we have 2 StartRoot \(2 x^3 y^4\) EndRoot StartRoot \(2^2\) EndRoot StartRoot \(x^2\) EndRoot StartRoot \(y^4\) EndRoot. Finally, we obtain 2 \(x^3 y^4\) StartRoot 2 x EndRoot, which is the expression in question.

(\(2 x y^2\) StartRoot 8 x^3 EndRoot)^2:

Expanding the expression inside the parentheses, we have \(2 x y^2\)StartRoot \((2^3) x^3\) EndRoot. Applying the exponent rule for square roots, we get \(2 x y^2\) StartRoot \(2^3\) EndRoot StartRoot \(x^3\) EndRoot.

Simplifying further, we have \(2 x y^2\) StartRoot 2 x EndRoot. Squaring the entire expression, we obtain (\(2 x y^2\) StartRoot 2 x EndRoot)^2.

Therefore, the expression (\(2 x^3 y^4\) StartRoot 2 x EndRoot)^2 is equivalent to StartRoot \(8 x^7 y^8\) EndRoot.

For more such questions on expression

https://brainly.com/question/1859113

#SPJ8