Point A is at 0 radians with coordinates (1, 0) on the unit circle. Point B is the result of
point A rotating- 5π/4 radians. Name two other angles of rotation that take A to B. At least one must be negative. Explain your reasoning.
Answers
The other angles of rotation that take point A to point B are -13π/4 radians (negative value) and 3π/4 radians (positive value).
How to get the angles of rotationWe can locate coterminal angles by adding or subtracting integer multiples of 2π (a full turn) to the given tilt.
The given angle is -5π/4 radians.
We will have to take away 8π/4 from the value above
-5π/4 - 8π/4 =
-13π/4
Hence the negative is -13π/4 radians.
Next we have to solve for the positive
-5π/4 + 8π/4
= 3π/4
Therefore the other angles of rotation that take point A to point B are -13π/4 radians (negative value) and 3π/4 radians (positive value).
Read more on angles of rotation here:https://brainly.com/question/2078551
#SPJ1
Related Questions
In 2000 your salary increased by 25% . In 2001 you received a 25% pay cut. After the two changes, how does your salary compare to your original salary
Answers
The answer is after these two changes, the salary is lower than the original.
The salary is lower (It is lower) after these two changes.
Given that,
- In 2000, salary increased by 25%
- in 2001, salary decreased by 25%
- Let the salary be X.
According to the scenario, the computation of given data are as follows.
\($$\begin{aligned}&\text { 2000 Salary }=1 X+(X \times 0.25) \\&=1.25 X \\&\mathbf{2 0 0 1} \text { salary }=1.25 X-(1.25 X \times 0.25) \\&=1.25 X-0.3125 X \\&=0.93 X\end{aligned}$$\)
Then, After these two changes, the salary is lower than the original.
What is the percentage?
A percentage is a number or ratio that may be stated as a fraction of 100 in mathematics. If we need to compute the percentage of a number, divide it by the entire and multiply by 100. As a result, the percentage denotes a part per hundred. The term % refers to one hundred percent. It is denoted by the sign "%."To learn more about percentage visit:
https://brainly.com/question/13450942
#SPJ4
what is -12 times -6 minus 3 to the 3rd power
Answers
\(\text{Hi! The Answer to your problem is 45}\)
\(\text {Multiply: (-12)*(-6)=72}\)
\(\text {3^3=27}\)
\(\text {Multiply: 3*3*3=27}\)
\(\text {Subtract: 72-27=45}\)
\(\text{Hey there!}\)
\(\bf{Do\ PEMDAS\ to\ answer\ this\ question}\)
\(\bf{{Parentheses}\)
\(\bf{Exponents}\)
\(\bf{Multiplication}\)
\(\bf{Division}\)
\(\bf{Addition}\)
\(\bf{Subtraction}\)
\(\bf{-12 \times (-6) - 3^3}\)
\(\bf{(-12)\times(-6) = \underline{72}}\)
\(\bf{72 - 3^3\ your\ new\ question\ for\ now}\)
\(\frak{3^3 = 3\times3\times3 = 9\times3 \rightarrow \underline{27}}\)
\(\bf{72 - 27 \ your\ new\ question}\)
\(\bf{72 - 27 = answer}\)
\(\frak{Solve\ above \ \& \ you\ have\ your\ answer\uparrow}\)
\(\text{Thus, your answer: \boxed{\bf{45}}}\checkmark\)
\(\text{Good luck on your assignment and enjoy your day!}\)
~\(\frak{LoveYourselfFirst:)}\)
A triangle has two sides of lengths 6 and 9. What value could the length of
the third side be? Check all that apply.
OA. 7
B. 2
C. 4
OD. 15
□E. 10
O F. 12
SUBMIT
Answers
B. 2 and OD. 15 are not possible lengths for the third side of the triangle.
To determine the possible values for the length of the third side of a triangle, we need to consider the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Given that two sides have lengths 6 and 9, we can analyze the possibilities:
6 + 9 > x
x > 15 - The sum of the two known sides is greater than any possible third side.
6 + x > 9
x > 3 - The length of the unknown side must be greater than the difference between the two known sides.
9 + x > 6
x > -3 - Since the length of a side cannot be negative, this inequality is always satisfied.
Based on the analysis, the possible values for the length of the third side are:
A. 7
C. 4
□E. 10
O F. 12
B. 2 and OD. 15 are not possible lengths for the third side of the triangle.
for such more question on lengths
https://brainly.com/question/24176380
#SPJ8
Order the decimal from least to greatest.
0.2, 0.17, 0.02, 0.72, 2.27
help me please
Answers
Answer:
0.02, 0.17, 0.2, 0.72, 2.27
Step-by-step explanation:
that's the answer!
Eliana is using a magnifying glass. The lens of the magnifying glass has a radius of 4 centimeters. What is the lens's area? Use 3.14 for pi.
Answers
Answer:
\(area = \pi {r}^{2} \\ = 3.14 \times {(4)}^{2} \\ = 50.24 \: {cm}^{2} \)
The Area of the lens is equal to 50.24 cm²
What is the area and circumference of a circle?The circumference (or) perimeter of a circle = 2πr units. The area of a circle = πr2 square units. Where r is the radius of the circle. The circumference of the circle or the perimeter of the circle is the measurement of the boundary of the circle. Whereas the area of the circle defines the region occupied by the circle.
Given here: Elliana is using a magnifying glass and radius of the magnifying glass has radius of 4 cm.
The formula for the area of a circle is A = πr², where r is the radius of the circle. The unit of area is the square unit, for example, m², cm², in², etc.
Thus Area of the lens of the glass is equal to A=πr²
=3.14×4²
=50.24 cm²
Therefore the len's Area is 50.24 cm²
Hence, The Area of the lens is equal to 50.24 cm²
Learn more about Area of a circle here:
https://brainly.com/question/14200825
#SPJ2
Someone plz help me :(

Answers
Answer:
i think it is c hope this help's
pic is Step-by-step explanation:

Answer:
quadrant III
Step-by-step explanation:
if 2 ordered pairs are (-x, -y)
that means they are in the quadrant III
the x-coordinate is negative and the y-coordinate is negative in an ordered pair: (−x, −y). For example: (−3, −5)
Solve - 2x - 15 = 6x + 9.
01) 3
2) -3
3) -1
4) 6
Answers
Answer:
the answer is the second one
Step-by-step explanation:
hoped I helped:)
3. The recycling center collects 343 aluminum cans in one day. How many cans will be collected in two weeks?
Answers
Answer:
4, 802 cans will be collected in two weeks
Step-by-step explanation:
343 aluminum cans = 1 day
? = 2 weeks
2 weeks = 14 days
So, 343 x 14 = 4, 802
Which is the better buy?
Frozen Peas
Cost (dollars)
Weight (ounces)
O Brand A
A B
2
16
3
28
O Brand B
O The unit cost is the same.
Answers
The better buy is given by the following brand:
Brand A.
How to obtain the better buy?The better buy is obtained applying the proportions in the context of the problem.
A proportion is applied as the cost per ounce is given dividing the total cost by the number of ounces.
Then the better buy is given by the option with the lowest cost per ounce.
The cost per ounce for each brand is given as follows:
Brand A: 16/2 = $8 per ounce.Brand B: 28/3 = $9.3 per ounce.$8 per ounce is a lesser cost than $9.3 per ounce, hence the better buy is given by Brand A.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
*97 POINTS*
Use the numerals representing cardinalities in the Venn diagram, shown on the right, to give the cardinality of the set
A' ∩ B' ∩ C. '
n(A' ∩ B' ∩ C')= ___________

Answers
Answer:
19
Step-by-step explanation:
A' represents everything out A
B' represents everything out B
C' represents everything out C
So only the outside is left hope this helps
You buy 3 pounds of lunch meat and pay $22.50. Write an equation that can be used to express the relationship between the total price, t, and the pounds of lunchmeat, p, you buy.
Select one:
t=3p
t=22.50p
t=9.25p
t=7.50p
help me!!
Answers
ILL GIVE BRAINLIEST
ALGEBRA 2 There are several methods for solving quadratic equations. But why don’t we use the same method every time? Wouldn’t that be easier?
What is your preferred method for solving quadratic equations? Describe the method in your own words and explain why you prefer it over the other methods.
What are the limitations of your preferred method?
Please follow these guidelines for your discussion posts:
Write at least 150–300 words.
Answers
Answer:
See below
Step-by-step explanation:
I'll provide an example to help you. Let's say we were solving \(x^2+5x-7=0\) and we wanted to factor the quadratic on the left side. We can't do that because the factors of -7 don't add up to 5. So we'd have to use the quadratic formula. The quadratic formula is essentially the last resort that will solve all quadratic equations, so it could be seen as a preferred method. But, unless you can factor the quadratic, it's much easier to solve.
Now let's do another one. \(x^2+5x+6=0\) for example can be written as \((x+2)(x+3)=0\) and we can easily get \(x=-2\) and \(x=-3\) as solutions since plugging them into the factors would produce 0 (from the Zero Product Property). If we used the quadratic formula, it would take more time to plug in the variables and solve when we can just simply factor.
Hopefully, this explanation helps you to think of your discussion post!
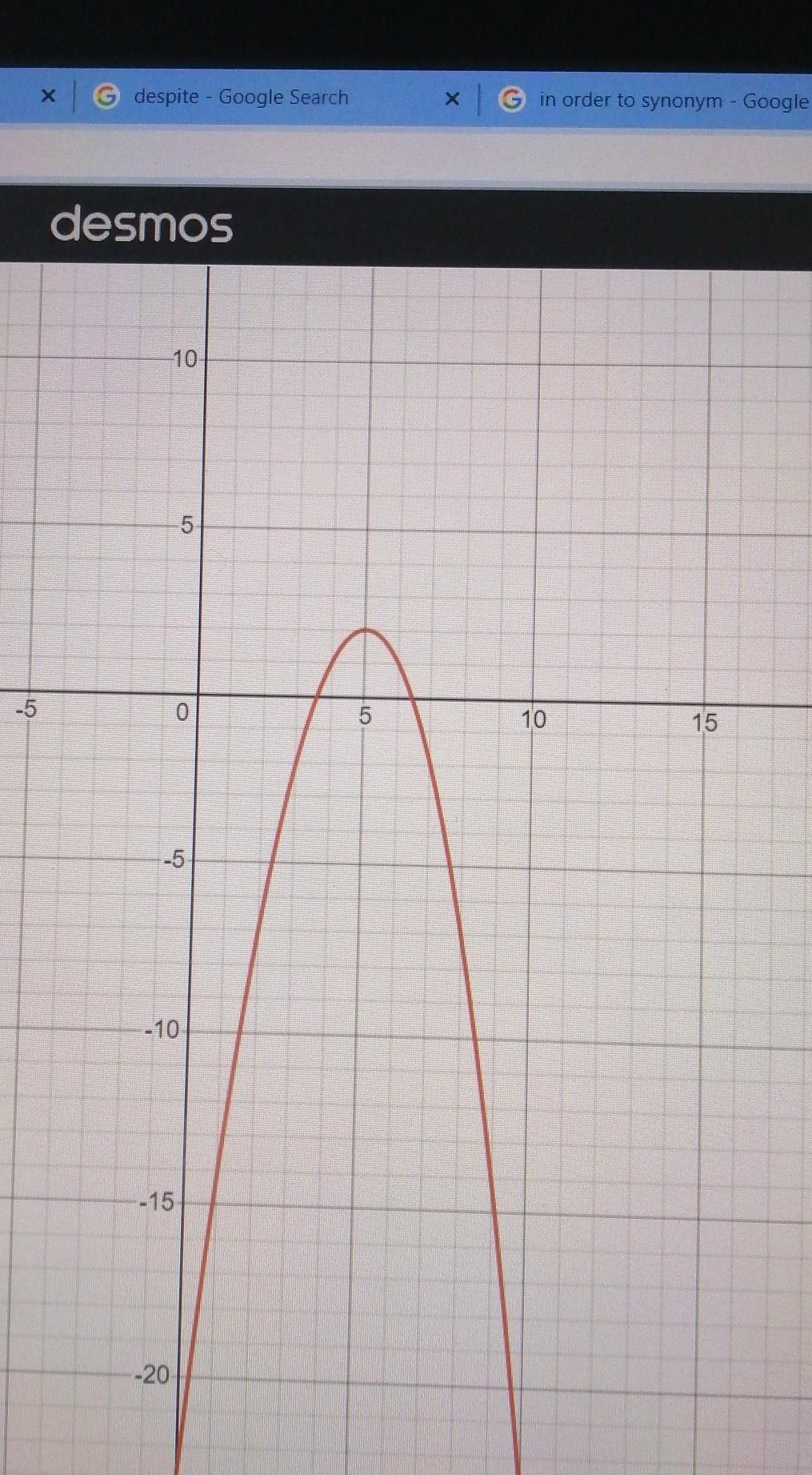
What is the graph for y = -x² + 10x - 23
Answers
Answer:
the maximum is (5,2)
y-int (0,-23)
Determine the value of y, if x is 9
y=\(x^{2}\)-8
Answers
Answer:
Step-by-step explanation:
y = x² - 8
put x= 9 you have y = (9)² - 8 =81-8 = 73
Correct answer gets brainliest

Answers
Answer:
Length.
Step-by-step explanation:
Any polygon's measurements include:
The number of sides of the shape. The angles between the sides of the shape. The length of the sides of the shape.
please mark brainliest:)
The level of cholesterol in the blood of women aged 20 to 55 in a particular country is normally distributed with mean 212 mg/dl and standard deviation 45.2 mg/dl.
The probability that the mean cholesterol level in a random sample of twenty such women is between 200 and 240 mg/dl is about
Can someone please show me how to do this on a TI84
Answers
The probability that the mean cholesterol level in a random sample of twenty women aged 20 to 55 is between 200 and 240 mg/dl is about 89.24%.
To find the probability that the mean cholesterol level in a random sample of twenty women is between 200 and 240 mg/dl using a TI-84 calculator, follow these steps:
1. First, calculate the standard error (SE) of the sample mean using the formula: SE = standard deviation / √(sample size). In this case, SE = 45.2 / √(20) ≈ 10.1.
2. Next, convert the lower and upper limits of the desired range (200 and 240) to z-scores using the formula:
z = (x - mean) / SE. For the lower limit, z1 = (200 - 212) / 10.1 ≈ -1.19. For the upper limit, z2 = (240 - 212) / 10.1 ≈ 2.77.
3. Now, turn on your TI-84 calculator and press the 2ND button followed by the VARS button to access the distribution menu. Scroll down and select "2: normalcdf(".
4. Enter the z-scores, lower limit, and upper limit as follows: normalcdf(-1.19, 2.77). Press ENTER.
5. The calculator will display the probability, which is approximately 0.8924 or 89.24%.
So, the probability that the mean cholesterol level in a random sample of twenty women aged 20 to 55 is between 200 and 240 mg/dl is about 89.24%.
To know more about "standard deviation" refer here:
https://brainly.com/question/23907081#
#SPJ11
If you add Natalie's age and Fred's age, the result is 38. If you add Fred's age to 3 times
the result is 62. Write and solve a system of equations to find how old Fred and Natalie
Natalie's age,
are.
Answers
The gypsy moth is a serious threat to oak and aspen trees. A state agriculture department places traps throughout the state to detect the moths. When traps are checked periodically, the mean number of moths trapped is only 0.6, but some traps have several moths. The distribution of moth counts is discrete and strongly skewed, with standard deviation 0.4.
a. What is the mean (±0.1) of the average number of moths x¯¯¯ (x bar) in 30 traps?
b. And the standard deviation? (±0.001)
Answers
The probability that the mean number of moths in a sample of size 50 is greater than or equal to 0.6 is 8.08%
The CLT states that the distribution of the sample means of a random variable with a finite mean and standard deviation approaches a normal distribution as the sample size increases.
In this case, the population mean is 0.5, and the population standard deviation is 0.7. Since we have a sample size of 50, the standard deviation of the sample means would be
=> 0.7 / √(50) = 0.099.
Next, we need to calculate the z-score, which measures the number of standard deviations from the mean.
In this scenario, we want to find the probability that the mean number of moths in a sample of size 50 is greater than or equal to 0.6. So, we would plug in x = 0.6, μ = 0.5, σ = 0.7, and n = 50 into the z-score formula. This gives us
=> (0.6 - 0.5) / (0.7 / √(50)) = 1.41.
Using a standard normal distribution table or calculator, we can find that the probability of a z-score of 1.41 or higher is approximately 0.0808. Therefore, the estimated probability that the mean number of moths in a sample of size 50 is greater than or equal to 0.6 is 0.0808 or about 8.08%.
To know more about standard deviation here.
https://brainly.com/question/16555520
#SPJ4
Complete Question:
The gypsy moth is a serious threat to oak and aspen trees. A state agriculture department places traps throughout the state to detect the moths. Each month, an SRS of 50 traps is inspected, the number of moths in each trap is recorded, and the mean number of moths is calculated. Based on years of data, the distribution of moth counts is discrete and strongly skewed, with a mean of 0.5 and a standard deviation of 0.7. Estimate the probability that the mean number of moths in a sample of size 50 is greater than or equal to 0.6.
Question 4: Linearize x** + 2x* + 2x^2 - 12x + 10 = 0. Around its equilibrium position
Answers
The linearized equation around its equilibrium position is given as;f(x) = -4.8(x - 1.39)
The given equation is x² + 2x* + 2x² - 12x + 10 = 0.
It needs to be linearized around its equilibrium position.
Linearizing the given equation around its equilibrium position x0, we have;
f(x) = f(x0) + f'(x0)(x - x0)
Where f(x) = x² + 2x* + 2x² - 12x + 10
The equilibrium position is the point where f(x) = 0.
Hence, f(x0) = 0.
Thus, x² + 2x* + 2x² - 12x + 10 = 0⇒ 3x² - 6x = -10⇒ x² - 2x + (2.33) = 0(x-1)² = 0.77x - 0.77 or
x = 1 + (0.77)/(2) or x = 1.39
Hence, the equilibrium position x0 = 1.39.
Substitute x0 = 1.39 in the equation and simplify to get f'(x0):
f(x) = x² + 2x* + 2x² - 12x + 10
f(x) = 3.84 - 8.34 + 10
f'(x0) = f'(1.39) = -4.8
Therefore, the linearized equation around its equilibrium position is given as;f(x) = -4.8(x - 1.39)
To more about linearized equation, click here
https://brainly.com/question/32634451
#SPJ11
Is the relation shown in the table below a function? Explain. Input 134 3 Output 1 9 16 27
Answers
Answer:
The relation is not a function
Step-by-step explanation:
First, it's important to know that for a relation to be a function, each input can only have one output. Since the input 3 has both the output 9 and 27, the relation can not be a function.
If this answer helped you, please leave a thanks or Brainliest!!!
Have a GREAT day!!!
Come up with an example for a solid, liquid, and gas describing the particle movement.
Answers
Answer:
Ice Cube, Liquid Water, and Steam
Step-by-step explanation:
An example of a solid is a ice cube, the particles are compacted together and there's very little movement.
An example of a liquid is water, the particles are more spread around and the movement is more frequent.
An example of a gas is steam, the particles are anywhere, moving fast and sporadic.
Samira babysits for 4. 5 hours and earns $22. 50. How much does she earn per hour?
P
Answers
Answer:
5$ per hour
Step-by-step explanation:
\( \frac{22.50}{4.5} = 5\)
Can someone help me find the answer to these 3 problems if so thank you .

Answers
Answer:
1. r+s²=49
2. pq²=24
3. -4xy-6x²+2x²y-6y= -54
Step-by-step explanation:
1. r+s²=0+7²=49
2. pq²=(6)(2)²=6(4)=24
3. -4xy-6x²+2x²y-6y= -4(3)(2)-6(3)²+2(3)²(2)-6(2)
= -24-6(9)+2(9)(2)-12
= -24-54+36-12
= -78+36-12
= -42-12
= -54
What is the exponential form of the expanded form below? 10.10.10.10.10. A 5.10 B 5)10 C 10)1. D 10)5
Answers
Answer:
the answer is D
Step-by-step explanation:
Answer: D AKA (10*5)
Step-by-step explanation:
I took the test on edge 2020 and it was correct!! and 10 5 times would make more sense being D which is 10*5 STAY SAFE :)What is the distance between (-5,3) and (3,3)?
Answers
Answer:
8
Step-by-step explanation:
Use the distance formula to determine the distance between two points.
true or false: if you are given a graph with two shiftable lines, the correct answer will always require you to move both lines.
Answers
False. if you are given a graph with two shif table lines, the correct answer will always require you to move both lines.
In a graph with two shiftable lines, the correct answer may or may not require moving both lines. It depends on the specific scenario and the desired outcome or conditions that need to be met.
When working with shiftable lines, shifting refers to changing the position of the lines on the graph by adjusting their slope or intercept. The purpose of shifting the lines is often to satisfy certain criteria or align them with specific points or patterns on the graph.
In some cases, achieving the desired outcome may only require shifting one of the lines. This can happen when one line already aligns with the desired points or pattern, and the other line can remain fixed. Moving both lines may not be necessary or could result in an undesired configuration.
However, there are also situations where both lines need to be shifted to achieve the desired result. This can occur when the relationship between the lines or the positioning of the lines relative to the graph requires adjustments to both lines.
Ultimately, the key is to carefully analyze the graph, understand the relationship between the lines, and identify the specific criteria or conditions that need to be met. This analysis will guide the decision of whether one or both lines should be shifted to obtain the correct answer.
Learn more about graph from
https://brainly.com/question/19040584
#SPJ11
Hoses A and B spout water at different constant rates, and hose A can fill a certain pool in 6 hours. Hose A filled the pool alone for the first 2 hours and the two hoses, working together, then finished filling the pool in another 3 hours. How many hours would it have taken hose B, working alone, to fill the entire pool
Answers
Answer:
18 hours
Step-by-step explanation:
Let the volume of the pool be x. Since pipe A filled the pool in 6 hours, the rate of pipe A = x / 6.
Let the rate of pipe b be y, Hose A filled the pool alone for the first 2 hours, this means that the volume filled in the 2 hours is x/6(2 hours) and the two hoses, working together, then finished filling the pool in another 3 hours for the 3 hours the volume filled is x/6(3) + y(3). hence the total time is:
x/6(2) + x/6(3) + y(3) = x
x/3 + x/2 + 3y = x
Multiply through by 6:
2x + 3x + 18y = 6x
5x + 18y = 6x
18y = x
y = x/18
The rate of pipe B is x/18, this means it would take pipe B 18 hours to full the pool alone
Water is flowing at the rate of 50m^3/min into a holding tank shaped like an cone, sitting vertex down. The tank's base diameter is 40m and a height of 10m.
A.) Write an expression for the rate of change of water level with respect to time, in terms of h ( the waters height in the tank).
B.) Assume that, at t=0, the tank of water is empty. Find the water level, h as a function of the time t.
C.) What is the rate of change of the radius of the cone with respect to time when the water is 8 meters deep?
Answers
A.) The rate of change of the water level with respect to time is (1/4) times the rate of change of the radius with respect to time. B.) The water level h as a function of time t is given by the equation h = 50t. C.) The rate of change of the radius of the cone with respect to time when the water is 8 meters deep is 200.
A.) To find the rate of change of the water level with respect to time, we need to use similar triangles. Let's denote the water level as h (the height of the water in the tank) and let's denote the radius of the water surface as r.
Since the tank is in the shape of a cone, we know that the ratio of the change in radius to the change in height is constant. Therefore, we can write:
(r/40) = (h/10)
To find the rate of change of the water level with respect to time (dh/dt), we differentiate both sides of the equation with respect to time:
(d(r/40)/dt) = (d(h/10)/dt)
Now, let's express the rate of change of the radius with respect to time (dr/dt) in terms of the rate of change of the water level with respect to time:
(dr/dt) = (40/10) * (dh/dt)
Simplifying this expression, we get:
(dr/dt) = 4 * (dh/dt)
Therefore, the rate of change of the water level with respect to time (dh/dt) is (1/4) times the rate of change of the radius with respect to time (dr/dt).
B.) To find the water level h as a function of time t, we need to integrate the rate of change of the water level with respect to time (dh/dt) over time. Since water is flowing into the tank at a constant rate of 50m^3/min, we can write:
dh/dt = 50
Integrating both sides with respect to time, we get:
∫dh = ∫50 dt
h = 50t + C
Since we are given that the tank is initially empty at t = 0, we can substitute h = 0 and t = 0 into the equation:
0 = 50(0) + C
C = 0
Therefore, the equation for the water level h as a function of time t is:
h = 50t
C.) To find the rate of change of the radius of the cone with respect to time when the water is 8 meters deep (h = 8), we can use the relationship we derived earlier:
(dr/dt) = 4 * (dh/dt)
We know that the rate of change of the water level with respect to time is dh/dt = 50. Substituting this into the equation, we get:
(dr/dt) = 4 * 50
(dr/dt) = 200
Therefore, the rate of change of the radius of the cone with respect to time when the water is 8 meters deep is 200.
To know more about rate of change,
https://brainly.com/question/1553593
#SPJ11
Part 1 of 2 Question content area top Part 1 A bee flies at 12 feet per second directly to a flowerbed from its hive. The bee stays at the flowerbed for 13 minutes, and then flies directly back to the hive at 8 feet per second. It is away from the hive for a total of 15 minutes. a. What equation can you use to find the distance of the flowerbed from the hive? b. How far is the flowerbed from the hive?
Answers
22
A rectangle's perimeter and its area have the same numerical value. The width of the rectangle is 3 units. What is
the length of the rectangle in UNS
Record your answer and fill in the bubbles on your answer document. Be sure to use the correct place value.
Answers
2.(x+3) = x×3.
2x + 6 = 3x.
x = 6 units is the answer :)