Answers
Related Questions
There are 14 students in a classroom with 4
tables. If 3 students can sit at a table, how
many students can sit down at tables?
Answers
A pentagon has 3 congruent sides and 2 other congruent sides. The perimeter of the pentagon is 36 centimeters. The three long congruent sides are 2 centimeters longer than the two shorter congruent sides.
Let x = length of a short side
Let y = length of a long side
The system of equations can be used to represent the situation.
y = x + 2
2x + 3y = 36
What is the length of one of the shorter congruent sides?
Answers
Answer:
Length of one of the shorter congruent side is: 6 cm
Step-by-step explanation:
In order to find the length of congruent sides we have to solve the system of equations
Given systems of equation is:
y = x + 2
2x + 3y = 36
Putting y = x+2 in second equation
\(2x + 3(x+2) = 36\\2x+3x+6 = 36\\5x+6 = 36\\5x = 36-6\\5x = 30\\\frac{5x}{5} = \frac{30}{5}\\x =6\)
As we know that x represents the shorter side, the length of short side is: 6 cm
Hence,
Length of one of the shorter congruent side is: 6 cm
Simplify the expression. 53 + 7(2 +3) - 52
Answers
Answer: 36
53 + 7(2 +3) - 52
53 + 7(5) - 52
53+35-52
88-52
36
Step-by-step explanation:
53+7(3+2)-52
According to BODMAS rule,
=53+7(5)-52
=53+35+52
=88-52
=36
The simplification of the given expression, 53+7(3+2)-52 is 36.
To know more about, BODMAS rule
https://brainly.com/question/25158415
Analytically show that the equations below represent trigonometric identity statements. 1. sec²θ (1-cos²θ) 2. cosx(secx-cosx) = sin²x 3. cosθ + sinθtanθ = secθ 4. (1- cos∝)(cosec∝+cot∝)= cos∝ tan∝
Answers
To show that the given equations represent trigonometric identity statements, we will simplify each equation and demonstrate that both sides of the equation are equal.
Starting with sec²θ(1 - cos²θ):
Using the Pythagorean identity sin²θ + cos²θ = 1, we can rewrite sec²θ as 1 + tan²θ. Substituting this into the equation, we get:
(1 + tan²θ)(1 - cos²θ)
= 1 - cos²θ + tan²θ - cos²θtan²θ
= 1 - cos²θ(1 - tan²θ)
= sin²θ
Thus, the equation simplifies to sin²θ, which is a trigonometric identity.
For cosx(secx - cosx) = sin²x:
Using the reciprocal identities secx = 1/cosx and tanx = sinx/cosx, we can rewrite the equation as:
cosx(1/cosx - cosx)
= cosx/cosx - cos²x
= 1 - cos²x
= sin²x
Hence, the equation simplifies to sin²x, which is a trigonometric identity.
Considering cosθ + sinθtanθ = secθ:
Dividing both sides of the equation by cosθ, we obtain:
1 + sinθ/cosθ = 1/cosθ
Using the identity tanθ = sinθ/cosθ, the equation becomes:
1 + tanθ = secθ
This is a well-known trigonometric identity, where the left side is equal to the reciprocal of the right side.
Simplifying (1 - cos∝)(cosec∝ + cot∝):
Expanding the expression, we have:
cosec∝ - cos∝cosec∝ + cot∝ - cos∝cot∝
= cot∝ - cos∝cot∝ + cosec∝ - cos∝cosec∝
= cot∝(1 - cos∝) + cosec∝(1 - cos∝)
= cot∝tan∝ + cosec∝sec∝
= 1 + 1
= 2
Thus, the equation simplifies to 2, which is a constant value.
In summary, we have analytically shown that the given equations represent trigonometric identity statements by simplifying each equation and demonstrating that both sides are equal.
To learn more about trigonometric identities click here: brainly.com/question/24377281
#SPJ11.
Problems (25 points each number) 1. Solve the following system 2x16x2x3 = -38 -3x1 - x₂ + 7x3 = 34 -8x1 + x2 - 2x3 = 20 using the Jacobi Method until the approximate error is less than 0.5% with the first approximations as x₁ = -2, x₂ = 4,23 = 3 Round-off intermediate values to 6 decimal places and the answer to 4 decimal places. How many iterations were made to solve the system? 2. Using the given in Example 1, solve using Gauss-Seidel Method. 3. Using Jacobi Method, obtain the solution to the system 1 + 5x2 + 3x3 = 30 3x1 + 7x2 + 13x3 = 80 12x1 + 3x25x3 = 2 (0) (0) with [20,20,20]= [1, 2, 3] until the approximate error is less than 1%. Round-off intermediate values to 7 decimal places and the answer to 5 decimal places. How many iterations were done to find the answer? 4. Using the given in Example 3, solve using Gauss-Seidel Method.
Answers
The general procedure for solving systems of linear equations using the Jacobi and Gauss-Seidel methods.
1.Jacobi Method:
Start with initial approximations for the variables in the system.
Use the equations in the system to calculate updated values for each variable, while keeping the previous values fixed.
Repeat the above step until the desired level of accuracy is achieved, usually by checking the relative or absolute error between iterations.
Count the number of iterations required to reach the desired accuracy.
2.Gauss-Seidel Method:
Start with initial approximations for the variables in the system.
Use the equations in the system to update the values of the variables. As you update each variable, use the most recent values of the other variables.
Repeat the above step until the desired level of accuracy is achieved, usually by checking the relative or absolute error between iterations.
Count the number of iterations required to reach the desired accuracy.
Note that both methods require careful handling of rounding and significant digits during the calculations to maintain accuracy.
To learn more about Gauss-Seidel visit:
brainly.com/question/13567892
#SPJ11
what's the answer pls
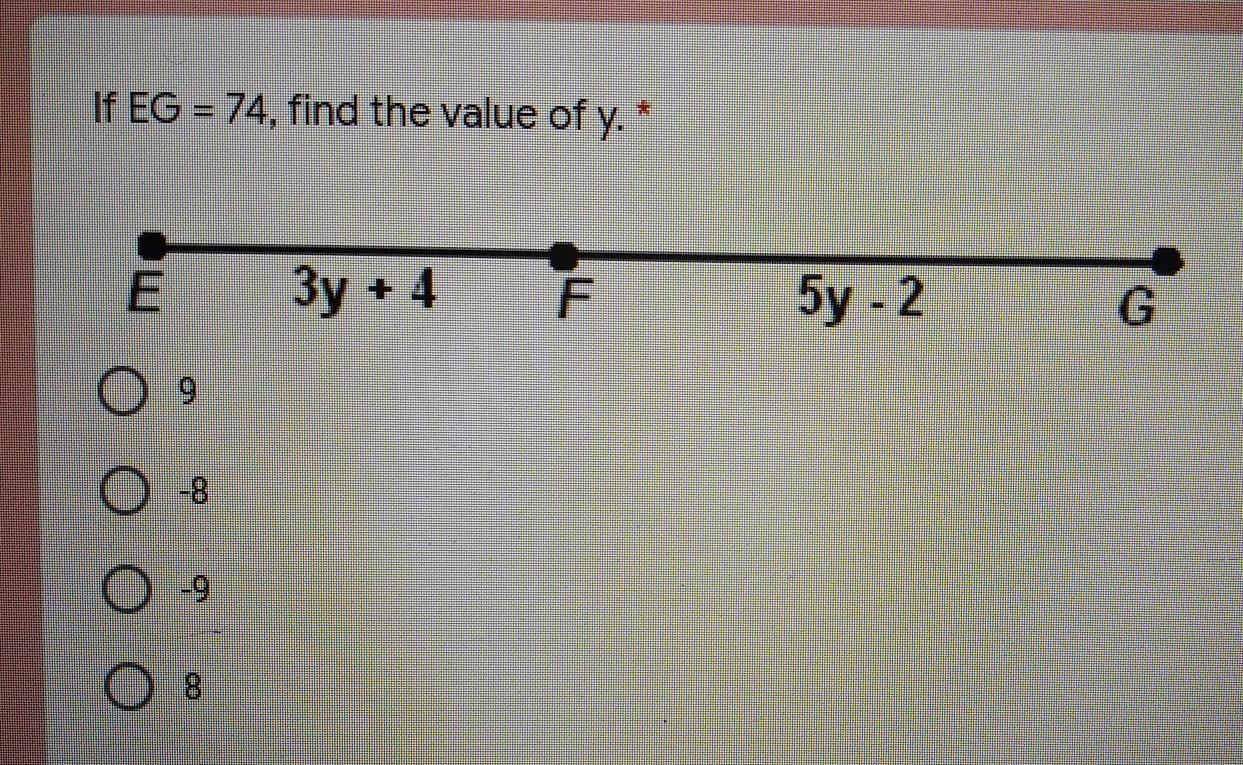
Answers
Answer this question

Answers
Since opposite angles of a parallelogram are equal, angle A = angle C and angle B = angle D where x is 35.
What is parallelogram?
A parallelogram is a four-sided flat shape in which opposite sides are parallel and have the same length. It is a type of quadrilateral, which means it has four sides.
The opposite angles of a parallelogram are also equal, which means that if angle A is equal to angle C, then angle B is equal to angle D. Moreover, the adjacent angles of a parallelogram are supplementary, which means that if angle A and angle B are adjacent angles, then angle A + angle B = 180 degrees.
According to the question:
Since AB = CD and angle A is 60 degrees, it means that opposite sides AB and CD are parallel and have the same length. Therefore, the figure ABCD is a parallelogram.
To determine the value of angle B, we can use the fact that the opposite angles in a parallelogram are equal. That is, angle B = angle D.
Since angle A + angle B + angle C + angle D = 360 degrees for any quadrilateral, we can write:
angle A + angle B + angle C + angle D = 60 + (3x+15) + angle C + angle D = 360
Simplifying this equation, we get:
4x + 75 + angle C + angle D = 360
angle C + angle D = 360 - 4x - 75 = 285 - 4x
Since angle B = angle D, we have:
angle B + angle D = 2 angle D = (3x+15)
Therefore, we can solve for angle D:
2 angle D = (3x+15)
angle D = (3x+15)/2
Now, we can substitute this into the equation for angle C + angle D:
angle C + (3x+15)/2 = 285 - 4x
Multiplying both sides by 2, we get:
2 angle C + 3x + 15 = 570 - 8x
Simplifying and solving for angle C, we get:
2 angle C = 555 - 11x
angle C = (555 - 11x)/2
Therefore, the angles of the parallelogram ABCD are:
angle A = 60 degrees
angle B = (3x+15) degrees
angle C = (555 - 11x)/2 degrees
angle D = (3x+15)/2 degrees
Note that since opposite angles of a parallelogram are equal, angle A = angle C and angle B = angle D.
To know more about parallelogram visit:
https://brainly.com/question/30577516
#SPJ1
Q. Determine the figure given below which has Angle A= 60 and Angle B=(3x+15)
61+x-1=90 find for x
Answers
Answer:
X = 30
Step-by-step explanation:

Answer:
x=30
Step-by-step explanation:
what is the quotient of the expression
\( \frac{21a {}^{3} b - 14ab {}^{2} + 7ab}{7ab} \)
Answers
In UVW the measure of W=90 the measure of U=39 and WU=96 feet. Find the length of UV to the nearest tenth of a foot.
Answers
Answer:
Step-by-step explanation:
123.5
Answer:123.5
Step-by-step explanation:
Write the first 4 terms of the sequence defined by the given rule.
4. f(n) = n³-1
Answers
The first four terms of the sequence defined by the rule f(n) = n³-1 are -1, 0, 7 and 26.
According to the question,
We have the following expression:
f(n) = n³-1
Now, in order to find the first four values of the given expression, we will change the values of n from 0 to 3.
So, putting the value of n as 0, we have:
f(0) = 0³-1
0-1 = -1
Now, putting the value of n as 1, we have:
1³-1
1-1
0
Now, putting the value of n as 2, we have:
2³-1
8-1
7
Now, putting the value of n as 3, we have:
3³-1
27-1
26
Hence, the first four terms of the sequence defined by the rule f(n) = n³-1 are -1, 0, 7 and 26.
To know more about terms of the sequence here
https://brainly.com/question/28615767
#SPJ1
7. an application of the distribution of sample means people suffering from hypertension, heart disease, or kidney problems may need to limit their intakes of sodium. the public health departments in some us states and canadian provinces require community water systems to notify their customers if the sodium concentration in the drinking water exceeds a designated limit. in connecticut, for example, the notification level is 28 mg/l (milligrams per liter). suppose that over the course of a particular year the mean concentration of sodium in the drinking water of a water system in connecticut is 26.4 mg/l, and the standard deviation is 6 mg/l. imagine that the water department selects a simple random sample of 32 water specimens over the course of this year. each specimen is sent to a lab for testing, and at the end of the year the water department computes the mean concentration across the 32 specimens. if the mean exceeds 28 mg/l, the water department notifies the public and recommends that people who are on sodium-restricted diets inform their physicians of the sodium content in their drinking water. use the distributions tool to answer the following question. (hint: start by setting the mean and standard deviation parameters on the tool to the expected mean and standard error for the distribution of sample mean concentrations.)
Answers
Based on the given information, we have the mean concentration of sodium in the drinking water of a water system in Connecticut as 26.4 mg/l and the standard deviation as 6 mg/l.
The water department selects a simple random sample of 32 water specimens over the course of a year. To answer the question using the distributions tool, we need to set the mean and standard deviation parameters on the tool to the expected mean and standard error for the distribution of sample mean concentrations.
The expected mean for the distribution of sample mean concentrations is the same as the mean concentration of sodium in the drinking water, which is 26.4 mg/l.
To know more about concentration visit:
https://brainly.com/question/30862855
#SPJ11
The water department in Connecticut is monitoring the concentration of sodium in their drinking water. By calculating the mean and standard error for the distribution of sample means, they can determine the probability of the mean concentration exceeding the notification level of 28 mg/l. If this probability is low, the water department will notify the public and recommend necessary actions.
In this scenario, the water department in Connecticut wants to monitor the concentration of sodium in their drinking water. They have set a notification level of 28 mg/l, meaning that if the mean concentration of sodium across a sample of 32 water specimens exceeds this level, they will notify the public.
To analyze this situation, we can use the distribution of sample means. The mean concentration of sodium in the drinking water of the water system is given as 26.4 mg/l, with a standard deviation of 6 mg/l.
To find the expected mean and standard error for the distribution of sample means, we can use the following formulas:
Expected mean of sample means = population mean
= 26.4 mg/l
Standard error of sample means = population standard deviation / square root of sample size
Using the given values, the standard error of sample means can be calculated as follows:
Standard error of sample means = 6 mg/l / square root of 32
≈ 1.06 mg/l
Now, we can use a distributions tool to find the probability that the mean concentration of sodium in the sample of 32 water specimens exceeds 28 mg/l. We will set the mean parameter on the tool to 26.4 mg/l and the standard deviation parameter to 1.06 mg/l.
By entering these values into the distributions tool, we can find the probability of obtaining a mean concentration greater than 28 mg/l. If this probability is less than a certain threshold (e.g., 0.05), it indicates that the mean concentration exceeding 28 mg/l is unlikely to occur by chance alone. In such cases, the water department would notify the public and recommend that individuals on sodium-restricted diets inform their physicians of the sodium content in their drinking water.
Learn more about concentration of sodium from the link:
https://brainly.com/question/17206790
#SPJ11
x^2+6x+5 factor each polynomial completely and if polynomial is prime, state this.
Answers
Solution
For this case we have the following polynomial
\(x^2+6x+5\)And we can factorize and we got:
\((x+5)(x+1)\)And the polynomial is not prime since can be factorized
create an expression with these conditions:the expression has 3 terms.the expression has a coefficient of 5.the expression has a constant of 8.move a number or variable to each line to create the expression.response area with 4 blank spacesblank space 1 empty plus blank space 3 empty blank space 4 empty plus blank space 7 emptyanswer options with 4 options.
Answers
The expression in the format "5(blank space 1) + (blank space 3)(blank space 4) + 8(blank space 7)" represents a mathematical expression with three terms. To create the expression with the given conditions, we can use the following format:
5(blank space 1) + (blank space 3)(blank space 4) + 8(blank space 7)
Here are four options for each blank space:
Option 1:
Blank space 1: x
Blank space 3: 2
Blank space 4: y
Blank space 7: z
So the expression would be:
5x + 2y + 8z
Option 2:
Blank space 1: a
Blank space 3: 3
Blank space 4: b
Blank space 7: c
So the expression would be:
5a + 3b + 8c
Option 3:
Blank space 1: m
Blank space 3: 4
Blank space 4: n
Blank space 7: p
So the expression would be:
5m + 4n + 8p
Option 4:
Blank space 1: r
Blank space 3: 1
Blank space 4: s
Blank space 7: t
So the expression would be:
5r + s + 8t
To know more about Mathematical Expression visit:
https://brainly.com/question/30997214
#SPJ11
A company's vice president's salary n years after becoming vice president is defined by the formula S(n) = 70000(1.2)". Which of the following statements is true? She will be receiving a 2% raise per year. Her salary will increase $14,000 every year. The rcent increase of her salary is 120% every year. Her salary is always 0.2 times the previous year's salary. The percent increase of her salary is 20% every year.
Answers
The correct statement is the percent increase of her salary is 20% every year. Hence, the answer is option E. Given that a company's vice president's salary n years after becoming vice president is defined by the formula S(n) = 70000(1.2)". We have to determine which of the following statements is true:
Given that a company's vice president's salary n years after becoming vice president is defined by the formula S(n) = 70000(1.2)". We have to determine which of the following statements is true:
She will be receiving a 2% raise per year. Her salary will increase $14,000 every year. The percent increase of her salary is 120% every year. Her salary is always 0.2 times the previous year's salary. The percent increase of her salary is 20% every year.
To calculate the salary of the vice president after n years of becoming a vice president, we use the given formula:
S(n) = 70000(1.2)
S(n) = 84000
The salary of the vice president after one year of becoming a vice president: S(1) = 70000(1.2)
S(1) = 84000
The percent increase of her salary is: S(n) = 70000(1.2)n
S(n) - S(n-1) / S(n-1) × 100%
S(n) - S(n-1) / S(n-1) × 100% = (70000(1.2)n) - (70000(1.2)n-1) / (70000(1.2)n-1) × 100%
S(n) - S(n-1) / S(n-1) × 100% = 20%
Therefore, the correct statement is the percent increase of her salary is 20% every year. Hence, the answer is option E.
To know more about salary visit:
https://brainly.com/question/14371457
#SPJ11
Find the circumference of a circle with a radius of 18 in. Leave your answer in terms of. 36πin. 18πin. 54πin. 324πin.
Answers
Answer:
36πin
Step-by-step explanation:
Formula for the circumference of a circle=2πr
r=18
2 · 18
=36
36·π
hope this helps
students are conducting an experiment to determine if the amount of sunlight affects the size of clover leaves. they plant clover in two identical pots, placing one next to a window and one inside a cupboard. they water each pot daily with 10 ml of water. which is the independent variable?
Answers
In the experiment, the independent variable is the amount of sunlight received by the clover plants.
The amount of sunlight the clover plants receive throughout the experiment serves as the independent variable, as it is being manipulated by the experimenters to determine its effect on the size of the clover leaves.
The dependent variable is the size of the clover leaves, which is being measured as a result of the change in the independent variable (amount of sunlight). The water is a controlled variable, as it is kept constant across both conditions to eliminate its effect on the outcome.
To learn more about variable here:
https://brainly.com/question/29521826
#SPJ4
a pentagon with 5 sides of equal length and 5 interior angles of equal measure is inscribed in a circle. is the perimeter of the pentagon greater than 26 centimeters?
Answers
the perimeter of the pentagon greater than 26 centimeters is given by
23.51
Given that a pentagon with 5 sides of equal length and 5 interior angles of equal measure is inscribed in a circle
The circle has area of 16 pi sq cm.
Hence radius of circle = 4 cm
The pengagon each side would be a chord of equal length subtending angle 72 at the centre.
visualize the triangle made by one side of pentagon with centre. This is isosceles with angles 72, 54 and 54
Use sine angle for this triangle.
, where R = radius =4 and s = side of pentagon.
s= 4.702
Perimeter = 5s = 23.5114 cm
Perimeter not greater than 26 cm.
If origin is at the centre then two vertices would be (4,0) (4cos 72, 4sin72),(4cos 144, 4 sin 144) and so on.
Longest diagonal = distance between (4,0) and (4cos 144, 4 sin 144)
= (-3.236, 2.351) and (4,0)
=7.608
Yes greater than 8 cm
learn more about of perimeter here
https://brainly.com/question/14368895
#SPJ4
A science experiment requires 493 milliliters of substance x and 14.5 milliliters of substance Y. Find the unit ratio of substance x to substance Y. What does your result mean in this situation?
Answers
The unit ratio of substance X to substance Y is 34:1. This means that for every 34 units of substance X, 1 unit of substance Y is required.
The unit ratio of substance X to substance Y in the science experiment is 493:14.5. This means that for every 493 milliliters of substance X used, 14.5 milliliters of substance Y is required.
A ratio is a comparison of two or more quantities of the same kind. Ratios can be expressed in different forms, but the most common is the unit ratio, which is the ratio of two numbers that have the same units. In this case, we are finding the unit ratio of substance X to substance Y, which is the amount of substance X required for a fixed amount of substance Y or vice versa.
We are given that 493 milliliters of substance X and 14.5 milliliters of substance Y are required for the science experiment. To find the unit ratio of substance X to substance Y, we divide the amount of substance X by the amount of substance Y:
Unit ratio of substance X to substance Y = Amount of substance X/Amount of substance Y
= 493/14.5
= 34:1
Therefore, the unit ratio of substance X to substance Y is 34:1. This means that for every 34 units of substance X, 1 unit of substance Y is required.
To know more about ratio here:
https://brainly.com/question/12024093
#SPJ11
12 less than four fifths of a number is three fifths of number increased by 15. what is the value of the number?
Answers
The value of the number is 135
Let 'm' be the required number.
We have been given a statement '12 less than four fifths of a number is three fifths of number increased by 15.'
We write given statement as a mathematical expression.
We can write '12 less than four fifths of a number ' as,
(4/5)m - 12
Also, we can write 'three fifths of number increased by 15' as (3/5)m + 15
so for statement, '12 less than four fifths of a number is three fifths of number increased by 15' we get an equation,
(4/5)m - 12 = (3/5)m + 15
Now we solve above equation to find the value of the m.
⇒ (4/5)m - 12 = (3/5)m + 15
⇒ (4/5)m - (3/5)m = 15 + 12
⇒ (4/5 - 3/5)m = 27
⇒ (1/5)m = 27
⇒ m = 27 × 5
⇒ m = 135
Therefore, the value of the number is 135
Learn more about an equation here:
https://brainly.com/question/21491044
#SPJ4
Kinda confused I need some assistance

Answers
The answer is mentioned below.
To graph these equations on the same coordinate plane, we can use x and y as our x-axis and y-axis respectively.y = 10 + 2x is a line with slope of 2 and y-intercept of 10y = 15 + x is a line with slope of 1 and y-intercept of 15The point of intersection, in this case (5,20), represents the system of equations' solution, and can be found by graphing those lines on the same plane.
How would you define transformation?
A transformation in mathematics is a function that modifies a geometric figure's position, size, or shape. It can be compared to a rule that instructs you on how to alter or move a figure. Transformations come in a variety of forms, including translations, rotations, reflections, and dilations.
A figure can be transformed into a different direction without changing its size or orientation by performing a translation.
A transformation known as a rotation revolves a figure around a fixed point.
We can begin by representing the world using algebraic equations.
In the library of G, y = 15 + x (since he began with 15 books and is currently adding one book per week).
There will eventually be an equal number of books in Greg's and Savannah's libraries, we are aware of this. In order to find x, we can set the two equations equal to one another as follows:
10 + 2x = 15 + x
Taking x away from both sides:
10 = 15 - x
x = 5
Thus, Greg and Savannah will have the same number of books in their libraries after five weeks. By substituting x = 5 into either equation, we can determine how many books that is:
y = 10 + 2(5) = 20
Therefore, after 5 weeks, both libraries will have 20 books.
To know more about function visit:
brainly.com/question/12431044
#SPJ1
35% off a phone = £78 how much was the phone before the discount prices?
Answers
Answer:
£120
Step-by-step explanation:
Given that
The price after reduction = £78
So, 65% = £78.
We have to calculate 100 %
To do so, find 5% and multiply that by 20
65% = £78
5% = 78/13 = £6
So, 100% = 6 x 20 = £120
Hope this helps.
Good Luck
Please mark brainiest
Need done by 08.00 today
An iron ball has a density of 6 g/cm3.
The volume of the ball is 13 cm3.
What is the mass of the ball?
Answers
Step-by-step explanation:
Mass = Density × Volume or m=pV
Density = 6
Volume = 13
6 × 13 = 78
The mass of the iron ball is 78.
===================================================
Work Shown:
d = density = 6 grams per cm^3
m = mass = unknown
v = volume = 13 cm^3
--------
d = m/v
dv = m
m = dv
m = 6*13
m = 78 grams
Robert wants to have 3 cherry trees planted on his property. He asked a landscaping company to give him a bid. The contractor wanted $750 to buy and plant the trees. Robert’s friend Tom said he would help him plant the trees on the weekend. The trees cost $115 each. How much will Robert save by having his friend help him?
Answers
Answer:
If I am correct he will save $405 by having his friend helping him.
Step-by-step explanation:
3x115=345
750-345=$405
totaled saved: 405
Let △ABC be a right triangle with m∠C = 90°. Given tan ∠B = 0.25, find tan ∠A. tan ∠A =
Answers
The solution of the given problem of triangle comes out to be tan ∠A = 0.25.
What exactly does a triangle mean?Triangles are called polygons if they have four quadrants or more. Its form is a simple geometric figure. When put together, the characters ABC create a right-angled triangle. When the boundaries are incompatible, Euclidean geometry generates a new rectangle with square corners. Triangles are regarded as polygons because they have three edges and three corners.
Here,
Since △ABC is a right triangle with m∠C = 90°, we know that m∠A + m∠B = 90°.
Using the fact that tan ∠B = opposite/adjacent, we can set up a ratio using a common factor, x, for the opposite and adjacent sides of ∠B:
tan ∠B = 0.25 = opposite/adjacent = x/4x
Simplifying the right side, we get:
0.25 = x/4x = 1/4
Multiplying both sides by 4x, we get:
x = 4
So the opposite side of ∠B has length x = 4, and the adjacent side has length 4x = 16.
Using the Pythagorean theorem, we can find the length of the hypotenuse of △ABC:
c² = a² + b²
c² = 4²+ 16²
c² = 256
c = √256
c = 16
Now, we can use the fact that tan ∠A = opposite/adjacent to find tan ∠A:
tan ∠A = opposite/hypotenuse = 4/16 = 1/4
Therefore, tan ∠A = 0.25.
To know more about triangle visit:
brainly.com/question/2773823
#SPJ1
Based on the following payoff table, answer the following: Buy Rent Lease Prior Probability The Bayes' decision rule strategy is: O Lease O Buy O High Alternative Low Rent High 90 70 60 0.44 Low -10 4
Answers
The Bayes' decision rule strategy is Buy.
Bayes' decision rule is used to choose between a set of mutually exclusive and collectively exhaustive outcomes based on the probabilities of those outcomes and their expenses. It chooses the decision alternative with the largest expected value. Bayes' decision rule specifies the following method for selecting between two mutually exclusive possibilities:
choose the one with the highest probability of being correct. Suppose we have two alternatives, A1 and A2, and we must select one. The outcomes O1, O2, and O3 may arise if we select A1, and outcomes O4, O5, and O6 may arise if we select A2, as shown in the given payoff table below:O1 O2 O3A1 r1 r2 r3A2 r4 r5 r6The procedure for using Bayes' rule is as follows:
Step 1: Calculate the likelihood ratios for each outcome. The likelihood ratio is the probability of the outcome given the chosen alternative divided by the probability of the outcome given the alternative not selected. For example, the likelihood ratio for O1 is as follows: r1/(r4 + r5 + r6).
Step 2: Estimate the prior probabilities of the alternatives (before any information is acquired). Assume that these are 50-50 probabilities unless more information is available. For example, if A1 and A2 are equally likely, their prior probabilities are both 0.50.
Step 3: Calculate the posterior probabilities of the alternatives given the observed outcome.
Bayes' theorem is used to calculate the posterior probabilities of the alternatives. The formula for Bayes' theorem is as follows: P(Ai|Oj) = (P(Oj|Ai)P(Ai))/ P(Oj)where P(Ai|Oj) is the posterior probability of Ai given Oj, P(Oj|Ai) is the likelihood of Oj given Ai, P(Ai) is the prior probability of Ai, and P(Oj) is the total probability of Oj, which is the sum of the likelihoods for the two alternatives.
Know more about decision rule here:
https://brainly.com/question/30074844
#SPJ11
2. Let A and B be invertible 5 x 5 matrices with det. A = 3 and det B = 8. Calculate: (a) det(A? B-) (b) det (24).
Answers
(a) The determinant of A inverse multiplied by B inverse is 3/8. (b) The determinant of 24 is 24 to the power of 5.
(a) We know that det(A) × det(A inverse) = 1, and similarly for B. So, det(A inverse) = 1/3 and det(B inverse) = 1/8.
Using the fact that the determinant of a product is the product of the determinants, we have det(A inverse × B inverse) = det(A inverse) × det(B inverse) = 1/3 × 1/8 = 1/24.
Therefore, det(A × B inverse) = 1/det(A inverse × B inverse) = 24/1 = 24.
(b) The determinant of a scalar multiple of a matrix is the scalar raised to the power of the dimension of the matrix.
Since 24 is a scalar and we are dealing with a 5 x 5 matrix, the determinant of 24 is 24 to the power of 5, or 24⁵.
To know more about determinant, refer here:
https://brainly.com/question/4470545#
#SPJ11
The parent function f(x)=x2 was reflected over the x-axis and translated 3 units left and 2 units down to form y=g(x).
Answers
The parent function f(x) = x² was reflected over the x-axis and translated three units left and two units down to form y = g(x). The function g(x) = - (x + 3)² - 2. is the correct anwer.
Here, the given parent function is f(x) = x².
We need to find the equation for the function g(x) which is obtained by reflecting the parent function f(x) = x² over the x-axis and translating it to three units left and two units down.
Therefore, the reflection of the parent function f(x) = x² over the x-axis gives the function h(x) = -x².
This function is obtained by negating all the y-coordinates of the parent function.
Then, we need to translate this function with three units left and two units down to obtain the function g(x).
Hence, the function g(x) = - (x + 3)² - 2.
Here, we obtain the desired equation for the function g(x) which is obtained by reflecting the parent function f(x) = x² over the x-axis and translating it to three units left and two units down.
This is the required solution to the given problem.
know more about parent function
https://brainly.com/question/17039854
#SPJ11
The function h is defined by h (x)=x²-1
Find h (5x)=
Answers
The value of h(5x) is 25x² - 1 given that the function h is defined by h(x) = x² - 1. This can be obtained by simply substituting the value 5x in the place of x in the function h(x).
Find the value of h(5x):A function takes an input and produces an output.
It is represented by notation f(x)
For example, f(x) = 2x²
f is the name of the function, x is the input of the function, and 2x² is the output of the function.
Here in the question it is given that,
The function h is defined by h(x) = x²-1We have to find the value of h(5x).
h(5x) is the output of h for the values 5x.
By substituting the value 5x in the place of x in the function h(x) = x² - 1.
h(5x) = (5x)² - 1
h(5x) = 25x² - 1
Hence the value of h(5x) is 25x² - 1 given that the function h is defined by h(x) = x² - 1.
Learn more about function here:
brainly.com/question/13387022
#SPJ9
The science club is going on a
field trip to the science
museum. The club has at most
$800 to spend on the trip. The
bus for the trip costs $100, and
meals at the museum cost
$4.50 per student. If admission
to the museum is $12 per
student and $16 per adult, and
there are six chaperones
attending, how many students
can go on the trip?
Answers
Answer:
36 students
Step-by-step explanation:
Equation: 800 = 100 + 4.5s + 12s + 96
Hope that helped! Can I also get brainliest? I need a few more to advance, if not thank you anyways and have a nice day!!!
Btw the answer is a decimal answer so I just kept 36, instead of rounding up or down.
Answer:
100+4.50(s)+12(s)+96⩽ 800
s=students
they can spend up to 800 dollars OR LESS. They have a charge of 100 dollars for the bus, plus a charge of 4.50 per student for lunches, plus a charge of 12 dollars per student for admissions plus 16 dollars times 6 (96) for the chaperones. All of this gives us our inequality above.
I really hope this helps!
PS: the reason why the adults don't get their own variable is because it says to define the variable not variable(s). You also cannot group the adults with the students because the student costs and the adult costs are two totally seperate and different amounts. if you just used variable p for people it wouldn't work because you wouldn't know how many adults were required to pay adult admission.
