Answers
5 3/4* 3 = 17.25 miles in an hour
First answer: 17.25 miles in an hour.
3a. True 3b. False 3c. True
Related Questions
Which statement is true about the polynomial -10m^n^+8m^n^+3m^n^-2m^n^-6m^n^ after it has been fully simplified?
Answers
Answer:
It has no undefined points.
Answer:
thats not a proper equation-
Step-by-step explanation:
Suppose y varies inversely with x, and y = 49 when x = 17
. What is the value of x when y = 7 ?
Answers
Answer:
119 is the value of x when y = 7
Step-by-step explanation:
Since y varies inversely with x, we can use the following equation to model this:
y = k/x, where
k is the constant of proportionality.Step 1: Find k by plugging in values:
Before we can find the value of x when y = k, we'll first need to find k, the constant of proportionality. We can find k by plugging in 49 for y and 17 for x:
Plugging in the values in the inverse variation equation gives us:
49 = k/17
Solve for k by multiplying both sides by 17:
(49 = k / 17) * 17
833 = k
Thus, the constant of proportionality (k) is 833.
Step 2: Find x when y = k by plugging in 7 for y and 833 for k in the inverse variation equation:
Plugging in the values in the inverse variation gives us:
7 = 833/x
Multiplying both sides by x gives us:
(7 = 833/x) * x
7x = 833
Dividing both sides by 7 gives us:
(7x = 833) / 7
x = 119
Thus, 119 is the value of x when y = 7.
25 cm 7 cm 15 cm what is the area of triangle
Answers
The area of the triangle with side lengths of 25 cm, 7 cm, and 15 cm is approximately 209.27 cm².
To calculate the area of a triangle with side lengths of 25 cm, 7 cm, and 15 cm, we can use Heron's formula, which is a formula for finding the area of a triangle when only the side lengths are known:
Area = √(s(s-a)(s-b)(s-c))
where s is the semi-perimeter of the triangle, and a, b, and c are the lengths of its sides. The semi-perimeter is half the sum of the three sides:
s = (a + b + c) / 2
Substituting the given values, we get:
s = (25 + 7 + 15) / 2 = 23.5
Now we can use Heron's formula to calculate the area:
Area = √(23.5(23.5-25)(23.5-7)(23.5-15))
= √(23.5 * (-1.5) * 16.5 * 8.5)
= √(43,822.5)
≈ 209.27 cm²
To learn more about triangles
https://brainly.com/question/2773823
#SPJ4
In the picture, lines a, b, and c are parallel. Simon and Adara set up correct but different proportions that can be used to find the unknown segment lengths in the diagram. Use the drop-down menus to complete the proportions.
Answers
When lines a, b, and c are parallel, we know that the corresponding angles are congruent. This means that if we draw a transversal line that intersects these parallel lines, the angles that are in the same position will have the same measures.
Both proportions are correct and can be used to find the unknown segment lengths in the diagram. It's important to note that these proportions only work when the lines are parallel. If the lines were not parallel, we would not be able to use corresponding angles to set up these proportions.
Using this information, we can set up proportions to find the unknown segment lengths. Let's look at Simon's proportion first:
Segment AD / Segment AC = Segment BD / Segment BC
In this proportion, we are comparing the lengths of two pairs of corresponding segments. We know that segment AD and segment BD are both parts of line segment AB, so we can substitute AB for AD + BD. Similarly, we can substitute AC for BC + AC. This gives us:
AB / AC = BD / B
Now we can cross-multiply to solve for the unknown segment length:
AB x BC = AC x BD
We can use the same process to solve for the unknown segment length in Adara's proportion. Her proportion is:
Segment AC / Segment AB = Segment CB / Segment BD
Using the same substitutions and cross-multiplication, we get:
AB x BD = AC x CB
To know more about congruent visit;-
https://brainly.com/question/12413243
#SPJ11
32/20 fully reduced in prime numbers
Answers
Answer:
8/5
Step-by-step explanation:
EL NUMERADOR Y EL DENONINADOR SE DIVIDEN AL MISMO TIEMPO
ENTRE LOS NÚMEROS PRIMOS EN ORDEN HASTA QUE YA NO PUEDAN
DIVIDIRSE.
Look at the graph below.

Answers
Answer:
B. -1/3
Step-by-step explanation:
Choose 2 points. From the lower points count up until it is in line with the other point. Then count left until you reach the second point.
Rise/Run
Rise=1
Run=-3
\(-\frac{1}{3}\)
Hope this helps!
Answer: -1/3 is the answer
Step-by-step explanation:
Which equation matches the table?

Answers
An equation that matches the table include the following: y = x + 5.
How to determine an equation of this line?In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):
y - y₁ = m(x - x₁)
Where:
m represent the slope.x and y represent the points.First of all, we would determine the slope of this line;
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (6 - 5)/(1 - 0)
Slope (m) = 1/1
Slope (m) = 1.
At data point (0, 5) and a slope of 1/, a linear equation in slope-intercept form for this line can be calculated by using the point-slope form as follows:
y - y₁ = m(x - x₁)
y - 5 = 1(x - 0)
y - 5 = x
y = x + 5
Read more on point-slope here: brainly.com/question/24907633
#SPJ1
what is the 6th term of the geometric sequence where a1 = −4,096 and a4 = 64? a. −1 b. 4 c. 1 d. −4
Answers
To find the 6th term of the geometric sequence, we first need to determine the common ratio (r) of the sequence. We can do this by using the formula for the nth term of a geometric sequence:
an = a1 * r^(n-1)
We know that a1 = -4,096 and a4 = 64, so we can substitute these values into the formula to get:
a4 = a1 * r^(4-1)
64 = -4,096 * r^3
Dividing both sides by -4,096 gives:
r^3 = -64/4096
r^3 = -1/64
Taking the cube root of both sides gives:
r = -1/4
Now that we know the common ratio is -1/4, we can use the formula for the nth term of a geometric sequence to find the 6th term:
a6 = a1 * r^(6-1)
a6 = -4,096 * (-1/4)^5
a6 = -4,096 * (-1/1024)
a6 = 4
Therefore, the 6th term of the geometric sequence is 4, so the answer is (b) 4.
To find the 6th term of the geometric sequence, we first need to determine the common ratio (r) of the sequence.
The 6th term of the geometric sequence where a1 = −4,096 and a4 = 64 is d. -4.
Given, a1 = -4096, a4 = 64We know that, the nth term of a geometric progression with first term a and common ratio r is given by an = ar^(n-1)Let's find the common ratio of the sequence.a4 = ar^3⟹64
= -4096r^3⟹r^3 = -\(\frac{64}{4096}\) = -\(\frac{1}{64}\)Thus, r = -\(\frac{1}{4}\)
The 6th term of the geometric sequence with first term a1 = -4096 and common ratio r = -\(\frac{1}{4}\) is given by;a6 = a1 * r^5Substituting the values of a1 and r, we get;a6 = -4096 * (-\(\frac{1}{4}\))^5⟹a6 = -4096 * \(\frac{1}{1024}\)⟹a6 = -4
To know more about geometric sequence Visit:
https://brainly.com/question/27852674
#SPJ11
6) write 36 + 60 as a product using the gcf as one of the factors.
36 + 60 =
?
?
+ ?
Answers
10 points
A pigeon flies for 7 hours at a speed of 70 km/h.
Calculate how far the pigeon flies.
Answers
Answer:
490km
Step-by-step explanation:
70km/hrs for 7hrs
so if the pigeon flies 70km in one hour we just have to multiply 70 by 7 to get 7hours.
70x7=490km
That means the pigeon flies 490km in 7hrs
Suppose that an individual has a body fat percentage of 12.1% and weighs 133 pounds. How many pounds of her weight is made up of fat? Round your answer
to the nearest tenth.
Answers
Answer:
1099.2 pounds
Step-by-step explanation:
Given data
Weight= 133 pounds
Percentage of far= 12.1%
Let the total fat be x
So
12.1/100*x= 133
0.121*x=133
x= 133/0.121
x= 1099.1735 pounds
x= 1099.2 pounds
HURRY 60 POINTS Question Consider the two-way table. Group 1 Group 2 Category A 36 20 Category B 12 35 Complete the table below to show the relative frequencies of the data in the first column. Enter numbers in the boxes as decimals to the hundredth place. Group 1 Category A Category B
Answers
Answer:
Category A 0.75
Category B 0.25
Hope it helps !!
At a Rubik's Cube competition, Martin solved the Rubik's Cube 5 times in 82.5 seconds.
On average, how long did it take him to solve the Rubik's Cube once?
Answers
Answer:
It takes him 16.5 seconds for each Rubik Cube
Step-by-step explanation:
Divide 82.5 by 5.
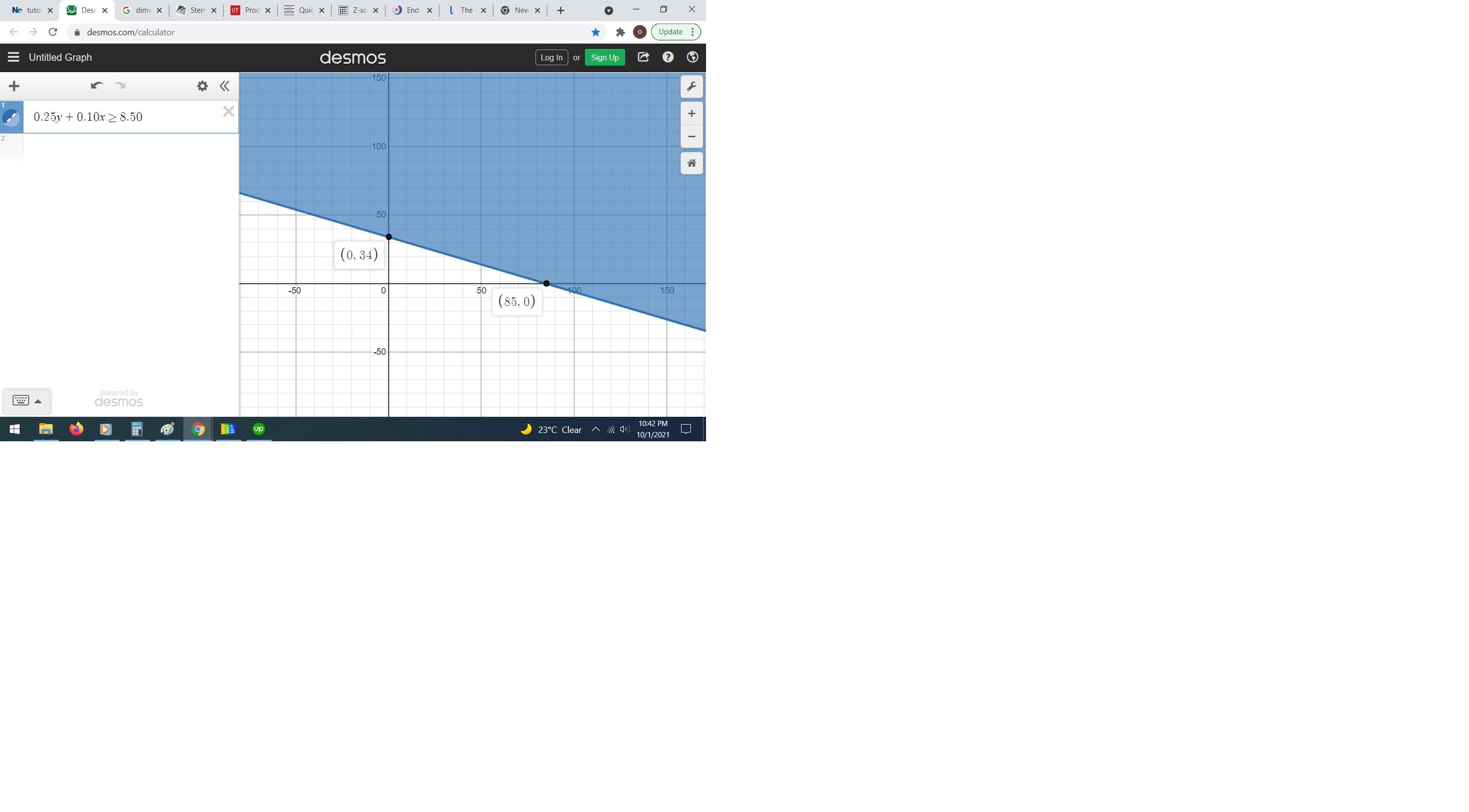
4. Tyler filled a small jar with quarters and dimes and donated it to his school'scharity club. The club member receiving the jar asked, "Do you happen toknow how much is in the jar?" Tyler said, "I know it's at least $8.50, but I don'tknow the exact amount."4a. Write an inequality to represent the relationship between the numberof dimes, d, the number of quarters, q, and the dollar amount of the moneyin the jar.
Answers
Let
y -----> number of quarters
x ----> number of dimes
we have that
the inequality that represents this situation is
Remember that
1 quarter =$0.25
1 dime=$0.10
so
\(0.25y+0.10x\ge8.50\)rewrite the variables
\(0.25q+0.10d\ge8.50\)see the attached figure to better understand the problem
Part 4b
The solution of the given inequality is the shaded area above the solid line 0.25q+0.10d=8.50
A solution to this inequality could be the point (50,50)
that means
the number of quarters is 50 and the number of dimes is 50
the ordered pair must satisfy the inequality
Verify
\(\begin{gathered} 0.25q+0.10d\ge8.50 \\ 0.25(50)+0.10(50)\ge8.50 \\ 12.50+5\text{ }\ge8.50 \\ 17.50\text{ }\ge8.50\text{ --}\longrightarrow\text{ is ok} \end{gathered}\)Part 4c
we have that
d=25 dimes
substitute in the inequality and solve for q
so
\(0.25q+0.10(25)\ge8.50\)solve for q
\(\begin{gathered} 0.25q+2.5\ge8.50 \\ 0.25q\ge8.50-2.5 \\ 0.25q\ge6 \\ q\ge24 \end{gathered}\)the number of quarters must be greater than or equal to 24
you are bored at a lunch meeting and surreptitiously place a raisin in your glass of water. the raisin swells to twice its original size. relative to the water, the raisin must have been:
Answers
If the raisin swells to twice its original size, relative to the water, the raisin must have been a)hypertonic solution. So, correct option is a.
Hypertonic alludes to an answer with higher osmotic strain than another arrangement. At the end of the day, a hypertonic arrangement is one in which there is a more noteworthy fixation or number of solute particles outside a layer than there are inside it.
A hypertonic arrangement is one which has a higher solute fixation than another arrangement.An illustration of a hypertonic arrangement is the inside of a red platelet contrasted and the solute centralization of new water.At the point when two arrangements are in touch, solute or dissolvable moves until the arrangements arrive at harmony and become isotonic concerning one another.Hence, correct option is a.
To know more about hypertonic solution, visit here:
https://brainly.com/question/29309024
#SPJ4
(Complete question) is:
You are bored at a lunch meeting and surreptitiously place a raisin in your glass of iced tea. The raisin shrinks to half its original size. The raisin must have been a __?__ solution.
a)hypertonic
b)aquatonic
c)hypotonic
d)isotonic
Identify the vertex of the parabola represented by the equation y=−2x2+8x−1.
(−4, −65)
(4, −1)
(2, 7)
(−2, −25)
Answers
Answer:
it is correct but -65 is not correct
Recognize functions from graphs, yes or no

Answers
Answer:
If your asking whether the graph shown is a function or not the answer is yes it is a function.
Step-by-step explanation:
There is a test called the vertical line test that states if you can draw a vertical line anywhere on the graph and it only passes through one point then the graph represents a function.
approximately what percentage of u.s. adults suffered from mental illness in 2016? responses 4.72% 4.72% 40.72% 40.72% 18.53% 18.53% 12.35%
Answers
According to the National Survey on Drug Use and Health, approximately 18.53% of U.S. adults (ages 18 and older) experienced some form of mental illness in 2016.
Approximately 18.53% of U.S. adults suffered from mental illness in 2016. This percentage represents the prevalence of mental health disorders among the adult population, which is important to understand in order to address and provide support for those affected.
This includes a range of conditions such as anxiety disorders, depression, bipolar disorder, and schizophrenia. It's important to note that mental illness can vary in severity and can impact individuals differently, and seeking professional help can greatly improve one's quality of life.
Learn more about quality of life here:
brainly.com/question/13826088
#SPJ11
What is the distance between (-3,7) and (-3,-4)
Answers
How does the graph f(x)=3(4)^x-6 + 2/3 relate to its parent function?
a. The Parent Function has been stretched.
b. The parent function has been translated up
c. The parent function has been translated to the right
d. The parent function has been compressed

Answers
f(x) → 3(4)ˣ⁻⁶ + 2/3 relate to its parent function.
What is function and example?
A function is a type of rule that produces one output for a single input. This is illustrated by the equation y=x2. Any input for x results in a single output for y. Considering that x is the input value, we would state that y is a function of x.We are given that
f(x)=3(4)^x-6 + 2/3
We have to find the graph of given function relate to its parent function.
Let parent function
g(x) = 4ˣ
Now, the graph shift 6 unit towards right by the rule of transformation
g(x) = g(x - 6 )
Therefore, by using this rule then, we get
g(x) = (4)ˣ⁻ ⁶
Now, stretch vertically 3 times the previous graph by using the rule of transformation
f(x) → 3f(x)
Now, after applying this rule we get
g(x) = 3(4)ˣ⁻⁶
Now, shift the graph 2/3 unit upward by the rule of transformation
f(x) → f(x) + 2/3
After applying this rule then, we get
f(x) → 3(4)ˣ⁻⁶ + 2/3
Learn more about function
brainly.com/question/12431044
#SPJ9
What is the image of N for a 300° counterclockwise rotation about the center of the regular hexagon? Will give brainiest only if answered correctly with explanation

Answers
Answer:
H
Step-by-step explanation:
here, the question says that the given regular hexagon needs to be rotated counter clockwise 300°, considering the edges labels, each movement from one edge to other is 60° as 360/6 =60.
focus on N and move on anti clockwise.
When N rotates anti clockwise about center from original to position G, is 60°,
when N moves on anti clockwise about center from original to position A is 120°.
similarly, to X is 180°, to E is 240° and to H is 300°.
so, the new position of N when rotated anti clockwise about origin of the hexagon will be at H.
4. Let M be the portion of the cylinder x2 + z2 = 1, os y < 3, oriented by unit normal N = (x, 0, z). (d) Verify the generalized Stokes's theorem (Theorem 3.2) for M and w = zdx + (x + y +z)dy-x dz.
Answers
The line integral becomes:
∫∂M w ⋅ dr = ∫(θ=0)(2π) [z(cosθ)d(cosθ) + (x + y + z)d(3) - x d(sinθ)]
What is Stoke's theorem?A statement regarding the integration of differential forms on manifolds, known as Stokes Theorem (also known as Generalised Stoke's Theorem), generalises and simplifies a number of vector calculus theorems. This theorem states that a line integral and a vector field's surface integral are connected.
To verify the generalized Stokes's theorem for the given surface M and vector field w, we need to evaluate both the surface integral of the curl of w over M and the line integral of w around the boundary curve of M. If these two values are equal, the theorem is verified.
First, let's calculate the curl of the vector field w:
curl(w) = (∂/∂x, ∂/∂y, ∂/∂z) x (z, x + y + z, -x)
= (1, -1, 1)
Next, we evaluate the surface integral of the curl of w over M. The surface M is the portion of the cylinder x² + z² = 1 where y < 3. Since M is a cylinder, we can use cylindrical coordinates (ρ, θ, z) to parameterize the surface.
The parameterization can be defined as:
r(ρ, θ) = (ρcosθ, ρsinθ, z), where 0 ≤ ρ ≤ 1, 0 ≤ θ ≤ 2π, and -∞ < z < 3.
To calculate the surface integral, we need to compute the dot product between the curl of w and the unit normal vector of M at each point on the surface, and then integrate over the parameter domain.
N = (x, 0, z)/√(x² + z²) = (ρcosθ, 0, ρsinθ)/ρ = (cosθ, 0, sinθ)
The surface integral becomes:
∬_M (curl(w) ⋅ N) dS = ∬_M (1cosθ - 1⋅0 + 1sinθ) ρ dρ dθ
Integrating over the parameter domain, we have:
∬_M (curl(w) ⋅ N) dS = ∫_(θ=0)(2π) ∫_(ρ=0)^(1) (cosθ - sinθ) ρ dρ dθ
Evaluating this double integral will yield the surface integral of the curl of w over M.
Next, we need to calculate the line integral of w around the boundary curve of M. The boundary curve of M is the intersection of the cylinder x² + z² = 1 and the plane y = 3. This is a circle of radius 1 in the xz-plane centered at the origin.
To parameterize the boundary curve, we can use polar coordinates θ. Let's denote the parameterization as γ(θ) = (cosθ, 3, sinθ), where 0 ≤ θ ≤ 2π.
The line integral becomes:
∫∂M w ⋅ dr = ∫_(θ=0)(2π) [z(cosθ)d(cosθ) + (x + y + z)d(3) - x d(sinθ)]
Learn more about Stoke's theorem on:
https://brainly.com/question/14040950
#SPJ4
A bell tolls every 10 minutes. Another bell tolls every 15 minutes. Both bells toll at 6:00 PM. They will toll together again at :
Answers
Answer:
I believe the next time both bells will ring at the same time is at 6:30PM.
Step-by-step explanation:
If the bells toll together at 6:00PM, the next time they toll together again should be at 6:30PM.(this is just how it works in my mind) if you add 15 to 15,, you get 30, right? And if you add 10+10=10, you get 30, right? And since 30 is a common number that both 10 and 30 can go into,, and is the lowest number both can go into,, it has to be the answer.
The joint and marginal pdf's of x = amount of almonds and Y = amount of cashews are
F(x,y) = fx(x) =
with fy(y) obtained by replacing x by y in fx(x). It is easily verified that Mu x = Mu y = A, and E(XY) = 2/ 5 Compute the correlation coefficient p for X and Y. P=
Answers
The correlation coefficient ρ for X and Y is ρ = -0.6675 in the given function.
What is correlation coefficient?The correlation coefficient is a statistical concept that aids in establishing a relationship between expected and actual values obtained through statistical experimentation. The calculated correlation coefficient's value explains why the difference between the predicted and actual values is so exact.
Correlation Coefficient value is always in the range of -1 to +1. A similar and identical relationship exists between the two variables if the correlation coefficient value is positive. Otherwise, it reveals how differently the two variables behave.
Pearson's correlation coefficient is calculated by taking the covariance of two variables and dividing it by the sum of their standard deviations. is typically used to represent it (rho).
The correlation coefficient is computed as,
\($ \rho & =\frac{{Cov}(X, Y)}{\sqrt{V(X)} \times \sqrt{V(Y)}}\)
\($=\frac{-0.0267}{\sqrt{0.04} \times \sqrt{0.04}}\)
= -0.6675
Thus, the correlation coefficient ρ for X and Y is ρ = -0.6675.
Learn more about correlation coefficient
https://brainly.com/question/15577278
#SPJ1
49. Use the system of inequalities below to complete part A through part C.
3x + y >= - 1
2y - 4 > 3x
Part A) Graph the system of inequalities and shade the solution set.
Part B) Is the point (1, 3) a solution to the system? Why or why not?
Part C) Determine 3 points that ARE solutions to the system.
Part D) Determine 3 points that ARE NOT solutions to the system.
Answers
A. The system of inequality is plotted and the graph is attached
B. (1, 3) is not a solution because it does not satisfy the two equations
C. the three points that are solutions are
(-1, 3) (-1, 4) (1, 4)How to find the solutions of the system of the equationsSubstituting the given point into the two system of equation if it satisfies the equation then it is a solution
For (1, 3)
3x + y ≥ - 1
3 * 1 + 3 ≥ - 1
6 ≥ - 1 correct
2y - 4 > 3x
2 * 3 - 4 > 3 * 1
2 > 3 - wrong hence not a solution
For (-1, 3)
3x + y ≥ - 1
3 * -1 + 3 ≥ - 1
0 > -1 correct
2y - 4 > 3x
2 * 3 - 4 > 3 * -1
2 > -3 correct this is a solution
(-1, 4) and (1, 4) other solutions are deduced form the attached graph where two the two shaded points intersect
Learn more about inequality graphs:
https://brainly.com/question/29334541
#SPJ1

Can someone help me?

Answers
Answer:
It's C the third answer choice
Step-by-step explanation:
I know this because since the arrow is pointing that direction the inequality arrow would too.
The reason I chose the one without the line Is because it's an open circle
Answer: x < 6
Step-by-step explanation: As you can see, the circle on the 6 is an empty circle, which means that it does not have an equal sign within it (the line thing that's under the sign) because if the circle is a full circle than it will have an equal sign within it, and if it's an empty circle than there will be no equal sign within it. And, the arrow is going to the left which means that it is a less than sign.
x - 1, x + 2 and 3x are the first three terms of an arithmetic sequence, find the first term and the fifth term by extracting the value of x.
Answers
Since they're in arithmetic progression, the difference between consecutive terms is fixed.
\((x + 2) - (x - 1) = 3\)
\(3x - (x + 2) = 2x - 2 = 3 \implies 2x = 5 \implies x = \dfrac52\)
Then the first term is
\(x-1=\dfrac52 - 1 = \boxed{\dfrac32}\)
and the fifth term is
\(3x + 3 + 3 = 3\cdot\dfrac32 + 3 + 3 = \boxed{\dfrac21}2\)
Find the particular solution of y"" – 4y' = 4x + 2e²x. x -2x 3 6 x² x 2x 4 6 + 2 6 x + 2 4 x 2x 2x x 3x + 2 4 2x
Answers
To find the particular solution of the given differential equation, we will use the method of undetermined coefficients.
The complementary solution of the equation is y_c(x) = c1 + c2e^(4x), where c1 and c2 are constants.
Now, let's find the particular solution yp(x) for the non-homogeneous part of the equation. Since the right-hand side contains terms of the form 4x and 2e^(2x), we assume the particular solution has the form yp(x) = Ax + Be^(2x), where A and B are constants to be determined.
Taking the first and second derivatives of yp(x), we have:
yp'(x) = A + 2Be^(2x)
yp''(x) = 4Be^(2x)
Substituting these into the differential equation, we get:
4Be^(2x) - 4(A + 2Be^(2x)) = 4x + 2e^(2x)
Simplifying the equation, we have:
(-4A + 2) + (-8B + 4) e^(2x) = 4x + 2e^(2x)
Comparing the coefficients on both sides, we get the following equations:
-4A + 2 = 0 (coefficient of e^(2x))
-8B + 4 = 4 (coefficient of x)
Solving these equations, we find A = 1/2 and B = 1/2.
Therefore, the particular solution is:
yp(x) = (1/2)x + (1/2)e^(2x)
The general solution of the given differential equation is the sum of the complementary solution and the particular solution:
y(x) = y_c(x) + yp(x) = c1 + c2e^(4x) + (1/2)x + (1/2)e^(2x)
Learn more about coefficients here
https://brainly.com/question/1038771
#SPJ11
I have a question with fractions 7/7 - 2/5I am suppose to estimate, and use compatible numbers
Answers
1
Explanation:
7/7 - 2/5
Using compatible numbers:
7/7 = 1 as it is closer and equal to 1
so we have: 1 - 2/5
2/5 is approximately 0 as it is closer to 0 than 1
= 1 - 0 = 1
7/7 - 2/5 using compatible number = 1
please someone help me with this question
4x-3=2x+7
Answers
more words because it wont send ;-;
