Answers
Is this a test? Cause im pretty sure this is cheating
Related Questions
A rectangular boad is 1100 millmeters long and 900 millmeters wide. what is the area of the board in square meters?
Answers
Answer:
1100 mm = 1.1 m, and 900 mm = 0.9 m.
So the area is 1.1 x 0.9 = 0.99 m^2
The area of the rectangular board is 0.99 square meters.
Given that a rectangular board is 1100 millimeters long and 900 millimeters wide.
We need to find the area of the board,
To find the area of the rectangular board in square meters, we need to convert the given dimensions from millimeters to meters and then calculate the area.
Given:
Length of the board = 1100 millimeters
Width of the board = 900 millimeters
To convert millimeters to meters, we divide the given values by 1000:
Length in meters = 1100 mm / 1000 = 1.1 meters
Width in meters = 900 mm / 1000 = 0.9 meters
The formula to calculate the area of a rectangle is:
Area = Length × Width
Substituting the values, we get:
Area = 1.1 meters × 0.9 meters
Area = 0.99 square meters
Therefore, the area of the rectangular board is 0.99 square meters.
Learn more about area of a rectangle click;
https://brainly.com/question/28570018
#SPJ4
6) Supplementary Exercise 5.51
A consumer advocate claims that 80 percent of cable television subscribers are not satisfied with their cable service. In an attempt to justify this claim, a randomly selected sample of cable subscribers will be polled on this issue.
(a)
Suppose that the advocate's claim is true, and suppose that a random sample of five cable subscribers is selected. Assuming independence, use an appropriate formula to compute the probability that four or more subscribers in the sample are not satisfied with their service. (Do not round intermediate calculations. Round final answer of p to 1 decimal place. Round other final answers to 4 decimal places.)
The answer for 6(a) is P( Xâ¥4) = P ( x = 4) + P (x = 5) = 5/4 * 0.84 * 0.21 + 5/5 * 0.85 * 0.20 = 0.737
(b)
Suppose that the advocate's claim is true, and suppose that a random sample of 25 cable subscribers is selected. Assuming independence, find each of the following: (Do not round intermediate calculations. Round final answer of p to 1 decimal place. Round other final answers to 4 decimal places.)
1.
The probability that 15 or fewer subscribers in the sample are not satisfied with their service.
The answer for 6(b)1 is P(Yâ¤15) = 1 - P( Y > 20) - X20, i = 16 P ( Y = i) = 1- 0.421 - 0.562 = 0.017
2.
The probability that more than 20 subscribers in the sample are not satisfied with their service.
The answer for 6(b)2 is
3.
The probability that between 20 and 24 (inclusive) subscribers in the sample are not satisfied with their service.
The answer for 6(b)3 is P(20 > Y < 24) = 1 - 0.421 - 0.1867 - 0.1358 - 0.0708 - 0.0236 = 0.1621
4.
The probability that exactly 24 subscribers in the sample are not satisfied with their service.
The answer for 6(b)4 is P( Y = 24) = 0.0236
(c)
Suppose that when we survey 25 randomly selected cable television subscribers, we find that 15 are actually not satisfied with their service. Using a probability you found in this exercise as the basis for your answer, do you believe the consumer advocate's claim? Explain. (Round your answer to 4 decimal places.)
Answers
Answer:
\(P(X \le 4) = 0.7373\)
\(P(x \le 15) = 0.0173\)
\(P(x > 20) = 0.4207\)
\(P(20\ge x \le 24)= 0.6129\)
\(P(x = 24) = 0.0236\)
\(P(x = 15) = 1.18\%\)
Step-by-step explanation:
Given
\(p = 80\% = 0.8\)
The question illustrates binomial distribution and will be solved using:
\(P(X = x) = ^nC_xp^x(1 - p)^{n-x}\)
Solving (a):
Given
\(n =5\)
Required
\(P(X\ge 4)\)
This is calculated using
\(P(X \le 4) = P(x = 4) +P(x=5)\)
This gives:
\(P(X \le 4) = ^5C_4 * (0.8)^4*(1 - 0.8)^{5-4} + ^5C_5*0.8^5*(1 - 0.8)^{5-5}\)
\(P(X \le 4) = 5 * (0.8)^4*(0.2)^1 + 1*0.8^5*(0.2)^0\)
\(P(X \le 4) = 0.4096 + 0.32768\)
\(P(X \le 4) = 0.73728\)
\(P(X \le 4) = 0.7373\) --- approximated
Solving (b):
Given
\(n =25\)
i)
Required
\(P(X\le 15)\)
This is calculated as:
\(P(X\le 15) = 1 - P(x>15)\) --- Complement rule
\(P(x>15) = P(x=16) + P(x=17) + P(x =18) + P(x = 19) + P(x = 20) + P(x = 21) + P(x = 22) + P(x = 23) + P(x = 24) + P(x = 25)\)
\(P(x > 15) = {25}^C_{16} * p^{16}*(1-p)^{25-16} +{25}^C_{17} * p^{17}*(1-p)^{25-17} +{25}^C_{18} * p^{18}*(1-p)^{25-18} +{25}^C_{19} * p^{19}*(1-p)^{25-19} +{25}^C_{20} * p^{20}*(1-p)^{25-20} +{25}^C_{21} * p^{21}*(1-p)^{25-21} +{25}^C_{22} * p^{22}*(1-p)^{25-22} +{25}^C_{23} * p^{23}*(1-p)^{25-23} +{25}^C_{24} * p^{24}*(1-p)^{25-24} +{25}^C_{25} * p^{25}*(1-p)^{25-25}\)
\(P(x > 15) = 2042975 * 0.8^{16}*0.2^9 +1081575* 0.8^{17}*0.2^8 +480700 * 0.8^{18}*0.2^7 +177100 * 0.8^{19}*0.2^6 +53130 * 0.8^{20}*0.2^5 +12650 * 0.8^{21}*0.2^4 +2300 * 0.8^{22}*0.2^3 +300 * 0.8^{23}*0.2^2 +25* 0.8^{24}*0.2^1 +1 * 0.8^{25}*0.2^0\)
\(P(x > 15) = 0.98266813045\)
So:
\(P(X\le 15) = 1 - P(x>15)\)
\(P(x \le 15) = 1 - 0.98266813045\)
\(P(x \le 15) = 0.01733186955\)
\(P(x \le 15) = 0.0173\)
ii)
\(P(x>20)\)
This is calculated as:
\(P(x>20) = P(x = 21) + P(x = 22) + P(x = 23) + P(x = 24) + P(x = 25)\)
\(P(x > 20) = 12650 * 0.8^{21}*0.2^4 +2300 * 0.8^{22}*0.2^3 +300 * 0.8^{23}*0.2^2 +25* 0.8^{24}*0.2^1 +1 * 0.8^{25}*0.2^0\)
\(P(x > 20) = 0.42067430925\)
\(P(x > 20) = 0.4207\)
iii)
\(P(20\ge x \le 24)\)
This is calculated as:
\(P(20\ge x \le 24) = P(x = 20) + P(x = 21) + P(x = 22) + P(x =23) + P(x = 24)\)
\(P(20\ge x \le 24)= 53130 * 0.8^{20}*0.2^5 +12650 * 0.8^{21}*0.2^4 +2300 * 0.8^{22}*0.2^3 +300 * 0.8^{23}*0.2^2 +25* 0.8^{24}*0.2^1\)
\(P(20\ge x \le 24)= 0.61291151859\)
\(P(20\ge x \le 24)= 0.6129\)
iv)
\(P(x = 24)\)
This is calculated as:
\(P(x = 24) = 25* 0.8^{24}*0.2^1\)
\(P(x = 24) = 0.0236\)
Solving (c):
\(P(x = 15)\)
This is calculated as:
\(P(x = 15) = {25}^C_{15} * 0.8^{15} * 0.2^{10}\)
\(P(x = 15) = 3268760 * 0.8^{15} * 0.2^{10}\)
\(P(x = 15) = 0.01177694905\)
\(P(x = 15) = 0.0118\)
Express as percentage
\(P(x = 15) = 1.18\%\)
The calculated probability (1.18%) is way less than the advocate's claim.
Hence, we do not believe the claim.
Geometry problem (possible drop down answers are ellipse rectangle and circle) please help! Will give crown to first to give correct answer.

Answers
Answer:
ellipses
a pair of parallel straight
Step-by-step explanation:
help it was meant to be turned in 8 minutes ago...

Answers
The length of the car in Ivans drawing is given as 8 cm
How to find the length of the carWe are to solve for the length of this car by using the figure we have in the scale drawing. The length of car in Megan's drawing is 6 cm. The scale is 3 : 2
Ivan's drawing is in the relation of 2 : 1 cm
We would have to find the actual length of this car but by the use of Megan's ratio
This is given as
6 * 2 / 3
12 / 3
= 4 cm
Next we have to find Ivans length.
4 * (2/1)
= 8 / 1
= 8 cm
Read more on length here: https://brainly.com/question/16557738
#SPJ1
у
= 5
16. Describe the following variation:
O A. y varies directly as X.
O B. y varies directly as the square of x.
O C. y varies inversely as the square of x.
O D. y varies inversely as x.
Answers
Answer:
I think it might be D
Step-by-step explanation:
Simplify the expression. What classification describes the resulting polynomial?
(8x2 + 3x) − (12x2 − 1)
Answers
The simplified expression is \(-4x^2 + 3x + 1\), which is a quadratic polynomial. Option D.
To simplify the expression \((8x^2 + 3x) - (12x^2 - 1)\), we can distribute the negative sign to each term within the parentheses:
\(8x^2 + 3x - 12x^2 + 1\)
Next, we can combine like terms by adding or subtracting coefficients of similar powers of x:
\((8x^2 - 12x^2) + 3x + 1\)
Simplifying further, we have:
\(-4x^2 + 3x + 1\)
The resulting polynomial \(-4x^2 + 3x + 1\) is a quadratic polynomial since it has a highest power of x^2 (the exponent of x is 2), which is\(-4x^2.\)Quadratic polynomials are polynomials of degree 2 and can be represented by a parabola when graphed.
In summary, the simplified expression \((8x^2 + 3x) - (12x^2 - 1)\) simplifies to \(-4x^2 + 3x + 1\) , which is a quadratic polynomial. So Option D is correct
For more question on quadratic visit:
https://brainly.com/question/1214333
#SPJ8
Note the complete question is

3(5 - 2x) + 2(x-3) plz help me quick:(
Answers
Answer:
9-4x is simplified
Step-by-step explanation:
hope this helps
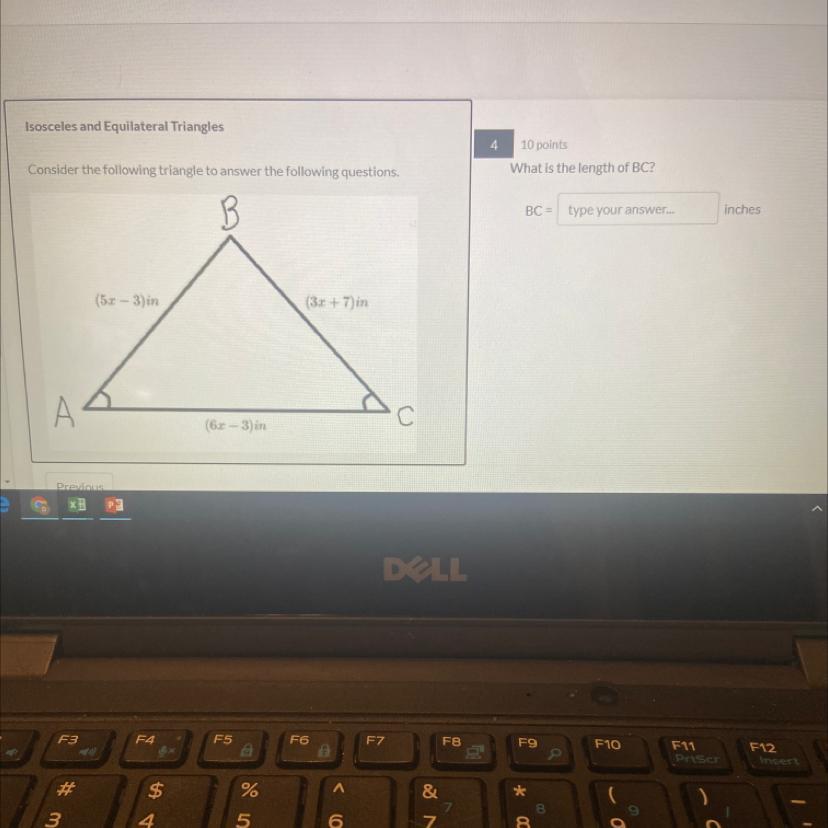
Suppose that the function h is defined, for all real numbers, as follows.
h(x) =
-2 if x-2
-1 if x=-2
Find h(-5), h (-2), and h (5).
h(-5) =
h (-2) = 0
h (5) = 0
8
X
S
Answers
The given function h(x) is h(-5) = -2, h(-2) = -1 and h(5) = -2.
What is the defined function for all real numbers?The set of all possible inputs is the domain of a function. For instance, all real integers other than x=0 are in the domain of f(x)=x2 and g(x)=1/x, respectively. Additionally, custom functions with more restricted domains can be defined.
The definition of the function h(x) is as follows:
h(x) =
-2 if x < 2
-1 if x = -2
Using this definition, we can find the values of h(-5), h(-2), and h(5) as follows:
h(-5): Since -5 < 2, we use the first part of the definition and set h(-5) = -2.
h(-2): Since -2 = -2, we use the second part of the definition and set h(-2) = -1.
h(5): Since 5 > 2, we use the first part of the definition and set h(5) = -2.
Therefore, we have:
h(-5) = -2
h(-2) = -1
h(5) = -2
To know more about function visit:-
https://brainly.com/question/12431044
#SPJ1
Someone has been shot! We found a blood drop that was measured to be 0.8 mm wide and 2.1 mm long.
The drop landed 5.1 feet away. How high up was the person shot?
Answers
The person was likely shot from a height between 3.8 and 30.1 mm above the location where the blood drop landed.
To determine how high up the person was shot, we can use the principles of projectile motion and the dimensions of the blood drop. Since we have the horizontal distance and the dimensions of the blood drop, we can assume that the drop followed a parabolic trajectory.
First, let's convert the distance from feet to meters for consistency. 5.1 feet is approximately 1.554 meters. Now, we need to calculate the time of flight. Since there is no information about the drop's initial velocity or angle, we cannot calculate the exact time. However, we can estimate it by assuming a reasonable range of velocities.
Let's assume the drop was traveling between 5 and 20 meters per second. With a distance of 1.554 meters, the estimated time of flight would be between 0.0777 and 0.311 seconds.
Next, we need to calculate the vertical displacement. We have the dimensions of the blood drop, with a width of 0.8 mm and a length of 2.1 mm. Assuming the drop maintained a spherical shape while in motion, we can take the average of the width and length to find the diameter. So, the diameter is approximately 1.45 mm, which is 0.00145 meters.
Using the estimated time of flight, we can calculate the vertical displacement using the formula:
Vertical displacement = (1/2) * g * t^2
where g is the acceleration due to gravity (approximately 9.8 m/s^2). Plugging in the estimated values, the vertical displacement ranges from 0.0038 to 0.0301 meters (3.8 to 30.1 mm).
Therefore, based on the given information, the person was likely shot from a height between 3.8 and 30.1 mm above the location where the blood drop landed.
For more such questions on shot,click on
https://brainly.com/question/30607987
#SPJ8
find the perimeter of OQR

Answers
The perimeter of the triangle OQR is 68 cm
How to determine the perimeter of the triangle OQRFrom the question, we have the following parameters that can be used in our computation:
Circles with the centers O, Q and R
When these centers are connected, the connection forms a triangle
The triangle OQR
Also from the question, we have the following values of radii
Radii = 8 cm, 11 cm and 15 cm
The perimeter of the triangle OQR is calculated as
Perimeter = Twice the sum of the radii
Substitute the known values in the above equation, so, we have the following representation
Perimeter = 2 *(8 + 11 + 15)
Evaluate the sum
Perimeter = 2 * 34
Evaluate the products
Perimeter = 68
Hence, the perimeter is 68 cm
Read more about perimeter at
https://brainly.com/question/18019422
#SPJ1
How many commutes are exactly 68 minutes

Answers
Answer:
three
Step-by-step explanation:
stem. is the tens place and the leaf is the. ones place
so you want to find 68 so you look in the stem column and look for six
in the row there are 6 numbers which mean:
60, 61, 67, 68, 68, 68
as you can see there is three 68 there for the answer ths 3
Emily made a pot cream of pumpkin soup for thanksgiving dinner she put 5 cups of cream in the soup she poured the soup into 24 small bowl show much cream measured in oz is used for each small bowl of soup?
Answers
Answer:
each bowl can contain 5/3 oz. of soup.
Step-by-step explanation:
1 cup = 8 oz.
8 oz.
5 cups x -------------- = 40 oz.
1 cup
to get the measurement of each bowl,
40 oz. divided into 24 bowls.
therefore, each bowl can contain 5/3 oz. of soup.
A line passes through -8,5 and has a slope of 3/4 write the equation in slope intercept form
Answers
The equation of the line in slope-intercept form is y = (3/4)x.
To write the equation of a line in slope-intercept form, we need to use the slope-intercept form equation: y = mx + b,
where m is the slope and b is the y-intercept.
Given that the line passes through the point (-8, 5) and has a slope of 3/4, we can substitute the values into the equation to find the y-intercept (b).
First, let's find the value of b using the point-slope form equation: y - y1 = m(x - x1), where (x1, y1) is a point on the line.
Using (-8, 5) as the point and 3/4 as the slope, we have:
5 - 5 = (3/4)(-8 - x)
0 = (3/4)(-8 - x)
0 = (-3/4)(8 + x)
0 = -6 - (3/4)x
Next, we can solve for x:
(3/4)x = -6
x = -6 \(\times\) (4/3)
x = -8
Now that we have the value of x, we can substitute it back into the equation to find the value of b:
0 = -6 - (3/4)(-8)
0 = -6 + 6
0 = 0
So, the value of b is 0.
Finally, we can write the equation of the line in slope-intercept form:
y = (3/4)x + 0
y = (3/4)x.
For similar question on slope-intercept form.
https://brainly.com/question/1884491
#SPJ8
Explain how to eliminate y from the given system of equations.
Answers
To eliminate y from the given system of equations, multiply the first equation by 2 and multiply the first equation by 3 and add them.
What is eliminate method to solve an equation?Utilizing the elimination approach is one strategy to resolve a linear system. To create an equation in one variable using the elimination approach, you can either add or subtract the equations.
To eliminate a variable, add the equations when the coefficients of one variable are in opposition, and subtract the equations when the coefficients of one variable are in equality.
If you don't already have equations that allow for the addition or subtraction of a variable, you can start by multiplying one or both equations by a constant to create an analogous linear system that allows for the addition or subtraction of a variable.
Given that, the linear equations are
2x + 3y = 6
3x – 2y = 4
To eliminate y from the given system of equations, multiply the first equation by 2 and multiply the first equation by 3 and add them.
To learn more about elimination method visit:
brainly.com/question/12691830
#SPJ1
The complete question is:
Explain how to eliminate y from the given system of equations.
2x + 3y = 6
3x – 2y = 4
What is the total area, in square feet, of the shaded sections of the trapezoid below? 100 points if you get the ANSWER CORRECT

Answers
Answer: 44.64ft^2
Step-by-step explanation:
Triangle 1:
A = 1/2 x 5.3 x 7.2
A = 19.08
Triangle 2:
A = 1/2 x 7.1 x 7.2
A = 25.56
25.56 + 19.08 = 44.64
Total area of triangles = 44.64ft^2
The type of graph used by precision teachers to track rate of learning and ensure the learner is on track for attaining fluency.
A. Line Graph
B. Scatterplot
C. Standard Celeration Chart
Answers
Standard Celebration Chart is used by precision teachers to track rate of learning and ensure the learner is on track for attaining fluency.
Since , It is a consistent display of frequency of change over time (celebration) precision teachers use it to track rate of learning and ensure the learner is on track for attaining fluency. The Standard Celebration Chart (initially called the Standard Behavior Chart) is used to observe and improve human learning and interaction. The chart shows the frequency of performance and its celebration, i.e., growth of learning across time.
Frequency, whose formula is
F = Count/Time,
Tells what happened during a specific time.
Celebration, whose formula is
C = Count/Time/Time, or Frequency/Time, tells what happens across the longer period of time – weeks, months, years, or decades.
All Standard Celebration Charts retain and present the original data in the form of frequency and celebration.
Learn more about Charts at
brainly.com/question/24741444
#SPJ1
Greg wants to buy a drum set he saw at the market. It costs $250. Greg has $123
How much more does he need? Type your answer in the box.
Answers
The amount Greg needed more to balance the cost of drum set if it cost $250 and he has $123 is $127
How to solve equation?Total cost of drum set = $250Amount with Greg = $123Amount needed = mTotal cost = Available amount + needed amount
250 = 123 + m
subtract 123 from both sides
250 - 123 = m
127 = m
Learn more about equation:
https://brainly.com/question/2972832
#SPJ1
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
Marcus has deposited $130 into a savings account each month this year. He plans on depositing $5 more per month into the savings account each year. How much money will Marcus deposit into the account each month in 7 years?
Answers
Answer: $420
Step-by-step explanation: 5x12x7
Convert the percent to a decimal
24 1/2%
Answers
Answer:
0.245
Step-by-step explanation:
24/1/2%=24.5%
=0.245
don’t mind the pencil writing

Answers
Answer:
Length = 22 cm
Width = 4 cm
Step-by-step explanation:
Area = 88 cm²
Length = x + 7
Width = x - 11
Area of rectangle = length*width
Therefore:
(x + 7)(x - 11) = 88
x(x - 11) +7(x - 11) = 88
x² - 11x + 7x - 77 = 88
Add like terms
x² - 4x - 77 = 88
x² - 4x - 77 - 88 = 88 - 88
x² - 4x - 165 = 0
Factorize
x² - 15x + 11x - 165 = 0
x(x - 15) +11(x - 15) = 0
(x + 11)(x - 15) = 0
x = -11 or x = 15
Let's use the positive number.
Therefore:
Length = x + 7
Plug in the value of x
Length = 15 + 7 = 22 cm
Width = x - 11 = 15 - 11 = 4 cm
The percent defective for parts produced by a manufacturing process is targeted at 4%. The process is monitored daily by taking samples of sizes n = 160 units. Suppose that today’s sample contains 14 defectives. Determine a 88% confidence interval for the proportion defective for the process today. Place your LOWER limit, rounded to 3 decimal places, in the first blank. For example, 0.123 would be a legitimate answer. Place your UPPER limit, rounded to 3 decimal places, in the second blank. For example, 0.345 would be a legitimate entry.
Answers
Answer:
The 88% confidence interval for the proportion of defectives today is (0.053, 0.123)
Step-by-step explanation:
In a sample with a number n of people surveyed with a probability of a success of \(\pi\), and a confidence level of \(1-\alpha\), we have the following confidence interval of proportions.
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which
z is the zscore that has a pvalue of \(1 - \frac{\alpha}{2}\).
For this problem, we have that:
\(n = 160, \pi = \frac{14}{160} = 0.088\)
88% confidence level
So \(\alpha = 0.12\), z is the value of Z that has a pvalue of \(1 - \frac{0.12}{2} = 0.94\), so \(Z = 1.555\).
The lower limit of this interval is:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.088 - 1.555\sqrt{\frac{0.088*0.912}{160}} = 0.053\)
The upper limit of this interval is:
\(\pi + z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.088 + 1.555\sqrt{\frac{0.088*0.912}{160}} = 0.123\)
The 88% confidence interval for the proportion of defectives today is (0.053, 0.123)
Right triangle with a hypotenuse of 159 ft and Angle A = 34 degree
Calculate the length of the sides they should be rounded to the nearest whole foot. The rounded for the legs (side) should be used to calculate the area of the triangle
Answers
the length of side a is 91 ft (rounded to the nearest whole foot) and the length of side b is 132 ft (rounded to the nearest whole foot). The area of the triangle is approximately 6007 sq ft.
Given: The hypotenuse of the right triangle,
c = 159 ft; angle A = 34°
We know that, in a right-angled triangle:
\($$\sin\theta=\frac{\text{opposite}}\)
\({\text{hypotenuse}}$$$$\cos\theta=\frac{\text{adjacent}}\)
\({\text{hypotenuse}}$$\)
We know the value of the hypotenuse and angle A. Using trigonometric ratios, we can find the length of sides in the right triangle.We will use the following formulas:
\($$\sin\theta=\frac{\text{opposite}}\)
\({\text{hypotenuse}}$$$$\cos\theta=\frac{\text{adjacent}}\)
\({\text{hypotenuse}}$$$$\tan\theta=\frac{\text{opposite}}\)
\({\text{adjacent}}$$\) Length of side a is:
\($$\begin{aligned} \sin A &=\frac{a}{c}\\ a &=c \sin A\\ &= 159\sin 34°\\ &= 91.4 \text{ ft} \end{aligned}$$Length of side b is:$$\begin{aligned} \cos A &=\frac{b}{c}\\ b &=c \cos A\\ &= 159\cos 34°\\ &= 131.5 \text{ ft} \end{aligned}$$\)
Now, we have the values of all sides of the right triangle. We can calculate the area of the triangle by using the formula for the area of a right triangle:
\($$\text{Area} = \frac{1}{2}ab$$\)
Putting the values of a and b:
\($$\begin{aligned} \text{Area} &=\frac{1}{2}ab\\ &=\frac{1}{2}(91.4)(131.5)\\ &= 6006.55 \approx 6007 \text{ sq ft}\end{aligned}$$\)
Therefore, the length of side a is 91 ft (rounded to the nearest whole foot) and the length of side b is 132 ft (rounded to the nearest whole foot). The area of the triangle is approximately 6007 sq ft.
For more question triangle
https://brainly.com/question/29135702
#SPJ8
Under the translation (X +3, y - 1) the point (3,4) will become (0.5)
True or False
Answers
9514 1404 393
Answer:
False
Step-by-step explanation:
Point (3, 4) will become (3+3, 4-1) = (6, 3), not (0, 5). The statement is False.
_____
Additional comment
The point (0, 5) would be translated to (3, 4). That is not what the question is asking.
13 different cut flowers and I plan on using 7 of them. How many different selections of the 7 flowers are possible?
Answers
Answer:
7/13
Step-by-step explanation:
Solve for x
X= ?
Linear Pairs of Angles

Answers
Answer:
x= 24
I hope it's helps you
One of the zeros of the polynomial function is 3.
f(x)=x4−x3−7x2+x+6
What is the factored form of the function?
f(x)=(x−3)2(x+1)(x+2)
f(x)=(x−3)(x+1)(x−1)(x+2)
f(x)=(x−3)(x+1)(x+2)2
f(x)=(x−3)(x+1)2(x+2)
Answers
Answer:
f(x)=(x−3)(x+1)(x−1)(x+2)
Step-by-step explanation:
What is an equation of the line that passes through the point ) (8,−5) and is parallel to the line
5x+4y=24?
Answers
By rearranging the equation, we get the equation of the line parallel to 5x + 4y = 24 that passes through the point (8, -5) as y = (-5/4)x + 5.To find the equation of a line parallel to another line, we need to determine the slope of the given line.
The equation of a line can be written in slope-intercept form as y = mx + b, where m represents the slope.
To determine the slope of the given line 5x + 4y = 24, we need to rearrange the equation in slope-intercept form. First, subtract 5x from both sides: 4y = -5x + 24. Next, divide all terms by 4: y = (-5/4)x + 6. Therefore, the slope of the given line is -5/4.
Since the line we are looking for is parallel to this line, it will also have a slope of -5/4. Now we can use the point-slope form of a line to find the equation. The point-slope form is given as y - y1 = m(x - x1), where (x1, y1) represents the given point (8, -5) and m is the slope.
Substituting the values into the equation, we have y - (-5) = (-5/4)(x - 8). Simplifying further, y + 5 = (-5/4)x + 10.
For more such questions on equation.
https://brainly.com/question/16949303
#SPJ11
Write an inequality that represents the graph below

Answers
An inequality that represents the given graph is; 2 < x < ∞.
What is referred as the term inequality?In mathematics, an inequality is a link between two expressions as well as values that aren't equal to each other.Inequality results from a lack of balance. For instance, suppose you would like to buy a new vehicle that costs $250 but only have 225. It is also a inequality because you are comparing these two non-equal numbers.For the given question.
The inequality is given by the values of the number line.
The value is starting from 2 and goes up to infinity.
But, It is a hollow dot at 2 means 2 is with open interval, as 2 will not be taken for the value of x.
The values lies between, (2, ∞)
Thus, the inequality that represents the given graph is; 2 < x < ∞.
To know more about the inequality, here
https://brainly.com/question/25799000
#SPJ13
Sebastian purchases two pieces of equipment for $109,000. Appraisals of the equipment indicate that the fair market value of the first piece of equipment is $76,300 and that the second piece of equipment is $119,900. What is Sebastians basis in these two assets?
Answers
Sebastian's basis in the two assets are: $42,389 and $66,611
How to calculate the total assets?The computation of the Sebastian's basis in these two assets is shown below:
= Market value of the first piece of equipment ÷ Total market value of two pieces of equipment × purchase value of two pieces of equipment
= ($76300 ÷ $(76300 + 119900)) × $109,000
= $42,389
= Market value of the second piece of equipment ÷ Total market value of two pieces of equipment × purchase value of two pieces of equipment
= ($119,900 ÷ $(76300 + 119900)) × $109,000
= $66,611
The Total market value of two pieces of equipment
= $(76300 + 119900)
= $196,200
Read more about Total Assets at: https://brainly.com/question/1169437
#SPJ1