Answers
Answer:
95 degrees
Step-by-step explanation:
25+60=85, and triangle's angles all equal 180, so 180-85=95
Related Questions
Determine the value of e. image attached.

Answers
Answer:
answer: b. 16
Step-by-step explanation:
8*4=32
32*0.5=
16
Which expression(s) is/are equivalent to 8-2(5x-3). Explain or show work to justify your decision.

Answers
8-10x + 6
8-(10x-6)
-10x+14
Answer:
B AND E (8-10x+6 & -10x+14)
Step-by-step explanation:
hope this helps !!!!!!!
QUICKKK!!!! how can you proof or check a point is a solution to a system of two linear equations?
Answers
To check to see if a point is a solution to a system of two linear equations, you can plug the points into each equation. If the solution point causes the equation toequal itself, it is correct.
Is 47/67 terminating, non terminating or repeating
Answers
Equivalen
Select two ratios that are equivalent to 27:9.
Answers
Answer:
3:1 & 54:18
Step-by-step explanation:
Answer: 9:3 and 3:1
Step-by-step explanation:
Glad I could help!
Only 1 and 2 pls helppp

Answers
Answer:
See the attached image for work.
1) The slope is 4.
2) The slope is 2.

Answer:
on the first one the rise is 20 and the run is 5. 5 divided by 20 is 4 so the slope is 4. I haven't answered the second one yet, sorry.
There are 50 sheets of drawing paper.
Larry divides the drawing paper between himself
and his younger brother John.
And Larry has 14 more sheets.
How many
sheets of drawing paper do Larry and his
brother have, respectively?
Answers
Answer:
John has 18 pieces of paper.
Larry has 32 pieces of paper.
Step-by-step explanation:
Let \(l\) be how many pieces of paper Larry has and \(j\) be how many pieces of paper John has.
We get:
\(j+14=l\)
\(j+l=50\)
\(j+j+14=50\\\\2j+14=50\)
Subtract 14 from both sides
\(2j=36\)
Divide both sides by 2
\(j=18\)
John has 18 pieces of paper.
\(j+14=l\\\\18+14=l\\\\l=32\)
Larry has 32 pieces of paper.
A rectangle has an area of 48 sq. in. and a perimeter of 28 in. Which of these could be the dimensions of the rectangle?
A) 4 inches by 7 inches
B) 4 inches and 12 inches
C) 3 inches by 8 inches
D) 6 inches by 8 inches
Answers
The possible dimensions of the rectangle are 6 inches by 8 inches, and the answer is D).
What is the area of rectangle?
The area of a rectangle is calculated by multiplying the length of the rectangle by its width. That is:
Area of rectangle = length × width
A = l × w
where A represents the area of the rectangle, l represents its length, and w represents its width.
Let's assume the rectangle has length "L" and width "W". We know that the area of the rectangle is 48 sq. in., so:
L * W = 48
We also know that the perimeter of the rectangle is 28 in., so:
2L + 2W = 28
L + W = 14
Now we can use these two equations to solve for L and W. One approach is to use substitution:
L = 14 - W (from the second equation)
(14 - W) * W = 48 (substituting for L in the first equation)
14W - W² = 48
W² - 14W + 48 = 0
(W - 6)(W - 8) = 0
So the possible values for W are 6 and 8. If W is 6, then L must be 8:
6 * 8 = 48 (the area checks out)
2(6) + 2(8) = 28 (the perimeter checks out)
Therefore, the possible dimensions of the rectangle are 6 inches by 8 inches, and the answer is D).
To know more about rectangles visit:
brainly.com/question/8663941
#SPJ1
Find the height of a prism with volume 720cm3 and base area 45cm2
Answers
Answer:
The height is 16 cm
Step-by-step explanation:
It's just v/b
720/45=16
The height is 16 cm
math pls help i’ve been stuck on this for the longest
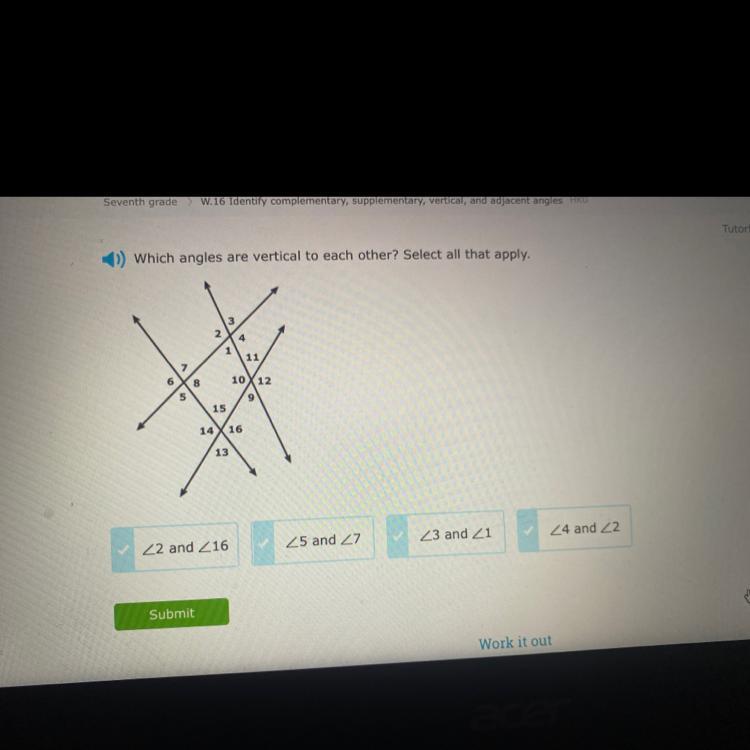
Answers
Basically it's almost everything but choice A
==================================================
Explanation:
When intersecting two lines to form an X shape, the vertical angles are the ones that form opposite one another. They do not have to align vertically, meaning they don't have to be stacked on top of one another. They could be side by side.
This applies to the following angle pairs
1 and 32 and 45 and 76 and 89 and 1110 and 1213 and 1514 and 16The items in bold apply to choices B through D
Side note: Vertical angles are always congruent.
Answer:
2nd, 3rd and 4th options
Step-by-step explanation:
when two lines intersect to make an X , angles on opposite sides of the X are called vertical angles. These angles are congruent.
from the listed angles the following are vertical angles.
∠ 5 and ∠ 7
∠ 3 and ∠ 1
∠ 4 and ∠ 2
Other vertical angles in the diagrm include
∠ 6 and ∠ 8
∠ 9 and ∠ 11
∠ 10 and ∠ 12
∠ 13 and ∠ 15
∠ 14 and ∠ 16
What is the sum of the measures of the exterior angles of the polygon shown below? If necessary, round to the nearest tenth.

Answers
The sum of the exterior angle of the pentagon is 360 degrees.
How to find the angles in a polygon?The polygon above is a pentagon. A pentagon is a polygon with 5 sides.
If the side of a polygon is extended, the angle formed outside the polygon is the exterior angle. The sum of the exterior angles of a polygon is 360°.
Therefore, the sum of the measure of the exterior angles of the pentagon as shown is 360 degrees.
learn more on polygon here: https://brainly.com/question/32120346
#SPJ1
Triangles E F G and K L M are shown. Angles E F G and K L M are congruent. The length of side K L is 6, the length of side M L is 5, and the length of K M is 8. The length of E G is 24, the length of G F is 15, and the length of E F is 18.
Can the triangles be proven similar using the SSS or SAS similarity theorems?
Yes, △EFG ~ △KLM only by SSS.
Yes, △EFG ~ △KLM only by SAS.
Yes, △EFG ~ △KLM by SSS or SAS.
No, they cannot be proven similar by SSS or SAS
Answers
Based on the given information, we cannot prove that △EFG and △KLM are similar using the SSS or SAS similarity theorems. The correct answer is option D) No, they cannot be proven similar by SSS or SAS.
To determine if the triangles △EFG and △KLM can be proven similar using the SSS (Side-Side-Side) or SAS (Side-Angle-Side) similarity theorems, we need to compare their corresponding sides and angles.
SSS Similarity Theorem states that if the lengths of the corresponding sides of two triangles are proportional, then the triangles are similar.
SAS Similarity Theorem states that if two corresponding sides of two triangles are proportional, and the included angles are congruent, then the triangles are similar.
Let's examine the given information:
Side lengths of △EFG: EF = 18, EG = 24, FG = 15.
Side lengths of △KLM: KL = 6, KM = 8, LM = 5.
By comparing the side lengths, we can see that they are not proportional. For example, the ratio of EF/KL is 18/6 = 3, while the ratio of EG/KM is 24/8 = 3. Therefore, the corresponding sides of △EFG and △KLM are not proportional, which means we cannot establish similarity using the SSS theorem.
Now, let's consider the SAS theorem. For this, we also need to compare the included angles.
Angles of △EFG: ∠EFG, ∠EFG, ∠EGF.
Angles of △KLM: ∠KLM, ∠KML, ∠KLM.
The given information states that ∠EFG and ∠KLM are congruent. However, we don't have any information about the other angles. Without knowing the congruency of the remaining angles, we cannot establish similarity using the SAS theorem
Option D.
For more such questions on theorems visit:
https://brainly.com/question/343682
#SPJ8
Answer: Its C
Step-by-step explanation:
Fill in each box to make the statements true.
The ____ function is written f(x) = ⌊x⌋ and rounds numbers ___ to the nearest integer. The graph of f(x) = ⌊x⌋ includes the point (174, ___ ).
Answers
One week, Lucy earned $234.00 at her job when she worked for 13 hours. If she is
paid the same hourly wage, how many hours would she have to work the next week to
earn $108.00?
Answers
Answer: 6 hours
Step-by-step explanation:divide 234 by 13 234/13 you get
18 divide 108 by 18 and then you get
6
The angle between the vectors a and b is 120 degrees and | a | =
3 | b |. Define the scalar λ such that a + b and a − λb are
perpendicular to each other.
Answers
The scalar λ can be given a value of -15.
We apply the principle of dot product and cross product between vectors to arrive at the solution.
The Dot Product of two vectors A and B is defined as:
A.B = |A|*|B|*Cosθ
where |A| and |B| are the magnitudes of the respective vectors.
Similarly, the Cross Product is defined as:
A×B = |A|*|B|*Sinθ * n,
where n is a vector perpendicular to both A and B.
Thus, A.B is a scalar quantity, but A×B is a vector.
We will apply both principles to arrive at a solution.
A+B and A-λB are perpendicular to each other.
Thus,
(A+B).(A-λB) = 0, since Cos90 = 0
A.A - λ(A.B) + B.A - λ(B.B) = 0
The dot product of a vector with itself is just the product of their magnitudes, as the angle between them is 0.
|A|² - λ|B|² + (1-λ)A.B = 0
A.B = |A|*|B| Cos 120 = -|A||B|/2 = -3|B|²/2 (Since |A| = 3|B|)
=> The prior equation can be further simplified as:
9|B|² - λ|B|² +(1-λ)(-3|B|²/2 ) = 0
|B|² {9 - λ +(3λ - 3)/2} = 0
Since |B| cannot be zero for obvious reasons, the rest of the expression is zero.
9 - λ +(3λ - 3)/2 = 0
18 - 2 λ + 3 λ - 3 = 0
λ = -15
Thus the scalar λ is equal to 15 for the two vectors to be perpendicular.
For more on Vector Products,
brainly.com/question/2005068
#SPJ4
graph y = 1/4 x I dont know how to do
Answers
(Excuse me if this doesn't make sense).
Your formula would be (4,1)
Your zero is (0,0)
To graph it:
If your y is 1, your x is 4
If your y is 2, your x is 8.
There's a video for this if my explanation and photo doesn't help

a right circular cylinder with radius 2 is inscribed in a hemisphere with radius 5 so that its bases are parallel to the base of the hemisphere. what is the height of this cylinder?
Answers
Answer:
Step-by-step explanation:
We can use the Pythagorean Theorem to find the height of the cylinder
We have
height = √ [ 5^2 - 2^2 ] = √[25 - 4] = √21 units
Find the volume V of the solid obtained by rotating the region bounded by the given curves about the specified line. y=x+1,y=0,x=0,x=4; about the x-axis V=
Answers
The given curves are `y = x + 1, y = 0, x = 0 and x = 4` and we are supposed to find the volume `V` of the solid obtained by rotating the region bounded by the given curves about the x-axis.
The region is shown below:Region bounded by y = x + 1, y = 0, x = 0 and x = 4We can observe that the region is a right-angled triangle with perpendicular `4` and base `1`. Now, we need to rotate this right-angled triangle about the x-axis to form a solid of revolution. The solid of revolution obtained is shown below:Solid of revolution obtained by rotating the region about the x-axis Since the region is rotated about the x-axis, the axis of rotation is `x-axis`.
So, the formula for volume of the solid of revolution is given by:`V = pi * ∫[a, b] y^2 dx`Here, the limits of integration are `a = 0` and `b = 4`.We need to express `y` in terms of `x`.Since, `y = x + 1`, we get`x = y - 1`Substituting this value of `x` in `x = 4`, we get`y - 1 = 4``y = 5`So, the limits of integration for `y` are `0 to 5`.So, we have to evaluate the integral:`V = pi * ∫[0, 5] (y - 1)^2 dx`
Simplifying this, we get:`V = pi * ∫[0, 5] (y^2 - 2y + 1) dy``V = pi * (∫[0, 5] y^2 dy - 2∫[0, 5] y dy + ∫[0, 5] dy)``V = pi * [y^3/3 - y^2 + y] [0, 5]``V = pi * [(5^3/3 - 5^2 + 5) - (0)]``V = pi * [(125/3 - 25 + 5)]``V = pi * [100/3]`
Therefore, the volume `V` of the solid obtained by rotating the region bounded by the given curves about the x-axis is `V = (100/3) pi` (in cubic units).
To know more about curves visit:
brainly.com/question/30543089
#SPJ11
a pizza parlor offers five sizes of pizza and 14 different toppings. a customer may choose any number of toppings (or no topping at all). how many different pizzas does this parlor offer?
Answers
Therefore, there are 81,920 different pizzas that this parlor offers.
Since there are five different sizes of pizza, a customer can choose any one of the five sizes. For each size, the customer can choose to have any combination of the 14 toppings, or no toppings at all. This means that for each size of pizza, there are $2^{14}$ different possible topping combinations, including the option of having no toppings. So the total number of different pizzas that the parlor offers is:
=5*2¹⁴
=5*16,384
=81,920
To know more about combination,
https://brainly.com/question/20211959
#SPJ11
Ray has tea. He has 2.671 liters of tea he pours 0.47 liters in a glass. how many liters did he pour? Solve.
Answers
On solving the given problem by help of mathematical operations, we got - After Ray poured 0.47L, he was left with 2.201L.
What does the term "mathematical operations" mean?The term "operation" in mathematics refers to the process of calculating a value using operands and a math operator. For the given operands or numbers, the math operator's symbol has predetermined rules that must be followed.
What are the five operations in mathematics?In mathematics, there are five basic operations: addition, subtraction, multiplication, division, and modular forms.
Total amount of tea Ray has - 2.671L
Amount of tea Ray poured - 0.47
Therefore,
amount he was left with was = 2.671- 0.47 = 2.201L
To know more about mathematical operations visit:
https://brainly.com/question/8959976
#SPJ9
Select an equivalent form of the problem below.
log5 25 - log5 100
Answers
Answer:
both are wrong
Step-by-step explanation:
If a ball is thrown into the air with a velocity of 40 ft/s, its height in feet after t seconds is given by y=40t−16t2.a) Find the average velocity for the time period beginning when t=2 and lasting(i) 0.5 seconds(ii) 0.1 second(iii) 0.05 seconds(iv) 0.01 secondb) Find the instantaneous velocity when t=2.
Answers
The average velocities for the given time periods has been calculated and the instantaneous velocity when t = 2 is -24 ft/s.
To find the average velocity for the given time periods, we need to calculate the change in position divided by the change in time. The formula for average velocity is:
Average Velocity = (Δy) / (Δt)
For the time period of 0.5 seconds:
Substituting t = 2 and t = 2.5 into the equation \(y = 40t - 16t^{2}\), we have:
\(y1 = 40(2) - 16(2^{2}) = 80 - 64 = 16 ft\)
\(y2 = 40(2.5) - 16(2.5^2) = 100 - 100 = 0 ft\)
Δy = y2 - y1 = 0 - 16 = -16 ft
Δt = 0.5 seconds
Average Velocity = (Δy) / (Δt) = (-16 ft) / (0.5 s) = -32 ft/s
For the time period of 0.1 seconds:
Substituting t = 2 and t = 2.1, we have:
\(y1 = 40(2) - 16(2^{2}) = 80 - 64 = 16 ft\\ y2 = 40(2.1) - 16(2.1^{2}) = 84 - 72.24 = 11.76 ft\)
Δy = y2 - y1 = 11.76 - 16 = -4.24 ft
Δt = 0.1 seconds
Average Velocity = (Δy) / (Δt) = (-4.24 ft) / (0.1 s) = -42.4 ft/s
For the time period of 0.05 seconds:
Substituting t = 2 and t = 2.05, we have:
\(y1 = 40(2) - 16(2^{2}) = 80 - 64 = 16 ft\\ y2 = 40(2.05) - 16(2.05^{2}) = 81 - 68.56 = 12.44 ft\)
Δy = y2 - y1 = 12.44 - 16 = -3.56 ft
Δt = 0.05 seconds
Average Velocity = (Δy) / (Δt) = (-3.56 ft) / (0.05 s) = -71.2 ft/s
For the time period of 0.01 seconds:
Substituting t = 2 and t = 2.01, we have:
\(y1 = 40(2) - 16(2^2) = 80 - 64 = 16 ft\\ y2 = 40(2.01) - 16(2.01^2) = 80.4 - 64.3216 = 16.0784 ft\)
Δy = y2 - y1 = 16.0784 - 16 = 0.0784 ft
Δt = 0.01 seconds
Average Velocity = (Δy) / (Δt) = (0.0784 ft) / (0.01 s) = 7.84 ft/s
To find the instantaneous velocity when t = 2, we need to calculate the derivative of the position function y(t) with respect to t.
Taking the derivative of \(y = 40t - 16t^{2}\) gives us the velocity function v(t):
\($v(t) = \frac{{d}}{{dt}} (40t - 16t^2) = 40 - 32t$\)
Substituting t = 2 into v(t), we have:
v(2) = 40 - 32(2) = 40 - 64 = -24 ft/s
Therefore, the instantaneous velocity when t = 2 is -24 ft/s.
Learn more about average velocity here:
https://brainly.com/question/28512079
#SPJ11
(8.6x107)-(9.1x10-8)simplify
Answers
Answer:
85,999,999.999 999 909
Step-by-step explanation:
The expression represents the difference of a relatively large number and one that is relatively small. That difference is approximately the value of the large number. The exact value requires 17 digits for its proper expression. Most calculators and spreadsheets cannot display this many digits.
Standard formThe numbers in standard form are ...
86,000,000 = 8.6×10^7
0.000000091 = 9.1×10^-8
DifferenceTheir difference is ...
86,000,000 -0.000000091 = 85,999,999.999 999 909
In scientific notation, this is ...
8.599 999 999 999 990 9×10^7
#10 Find the volume of the cylinder and round to the nearest tenth. *
1 point
9 cm
10 cm
Answers
Answer:
Step-by-step explanation:
This Website is On Goo gle By the way!

Need help, urgent please
In triangle ABC, a = 6, b = 9 & c = 11. Find the
measure of angle C in degrees and rounded to 1 decimal place.
Answers
Answer: The measure of angle C in degrees and rounded to 1 decimal place is approximately 131.8.
Explanation: In triangle ABC, a = 6, b = 9 & c = 11. To find the measure of angle C in degrees and rounded to 1 decimal place, we can use the Law of Cosines. The Law of Cosines states that for any triangle ABC:
\($$c^2 = a^2 + b^2 - 2ab \cos(C)$$\\Rearranging the equation:$$\cos(C) = \frac{a^2 + b^2 - c^2}{2ab}$$\)
Substituting the given values :
\($$\cos(C) = \frac{6^2 + 9^2 - 11^2}{2(6)(9)}$$\\Solving for cos(C): $$\cos(C) = \frac{-2}{3}$$\)
Now, using the inverse cosine function, we can find the value of C in degrees:
\($$C = \cos^{-1}\left(\frac{-2}{3}\right)$$\\ Rounding to 1 decimal place:\\$$C \approx 131.8^\circ$$\)
Therefore, the measure of angle C in degrees and rounded to 1 decimal place is approximately 131.8.
To know more about inverse cosine function visit :
https://brainly.com/question/14345853
#SPJ11
Find the missing term.
Replace the question mark (?) with (Drop down box) to make the equation true.
Answers in the drop down box...... A.) m+n B.) 0 C.) m-1 D.) -(m+n)

Answers
Equations are used to relate equal expressions.
The missing term is: \(\mathbf{ m -1}\)
The equation is given as:
\(\mathbf{\frac{m - n}{m^2 - n^2} + \frac{?}{(m -1)(m -n)} = \frac{2m}{m^2 - n^2}}\)
Express \(\mathbf{m^2 - n^2\ as\ (m - n)(m + n)}\)
So, we have:
\(\mathbf{\frac{m - n}{(m - n)(m + n)} + \frac{?}{(m -1)(m -n)} = \frac{2m}{(m - n)(m + n)}}\)
Multiply through by \(\mathbf{m - n}\)
\(\mathbf{\frac{m - n}{m + n} + \frac{?}{m -1} = \frac{2m}{m + n}}\)
Collect like terms
\(\mathbf{ \frac{?}{m -1} = \frac{2m}{m + n} - \frac{m - n}{m + n}}\)
Take LCM
\(\mathbf{ \frac{?}{m -1} = \frac{2m - m + n}{m + n} }\)
\(\mathbf{ \frac{?}{m -1} = \frac{m + n}{m + n} }\)
Divide \(\mathbf{ \frac{m + n}{m + n} }\)
\(\mathbf{ \frac{?}{m -1} = 1}\)
Cross multiply
\(\mathbf{ ? =(m -1)\times 1}\)
\(\mathbf{ ? =m -1}\)
Hence, the missing term is: \(\mathbf{ m -1}\)
Read more about equations at:
https://brainly.com/question/15668451
Which ordered pair is a solution of the system of equations? y= 3x + 1 y= 5x - 1 A (2,3) © (1,2) B (0, 1) D (1,4)
Answers
Answer:
D
Step-by-step explanation:
So first, we have to test the pairs. Let start with equation 1.
7=\=3 x
4=\=2 x
0=0 ✓
4=4 ✓
Now we only have to test B and D.
0=\=-1
4=4 ✓
D is the correct answer.
Which statement best describes parallel lines?
Parallel lines intersect at exactly one point.
Parallel lines intersect at exactly one point. ,
Parallel lines intersect infinitely many times.
Parallel lines intersect infinitely many times. ,
Parallel lines have equal slopes.
Parallel lines have equal slopes. ,
Parallel lines have negative reciprocal slopes.
Answers
Answer:
Step-by-step explanation:
Parallel lines have identical slopes and different y intercepts.
y = 3x + 2
y = 3x + 9
These lines are parallel with the same slopes (3) and different y intercepts (2 and 9)
Solve the following quadratic equation for all values of x in simplest form.
3(x-5)^2=33
Answers
The value of x for the given quadratic expression is x = 5 ± √11.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given expression is 3(x-5)²=33. The value of x will be calculated as,
3(x-5)²=33
(x - 5 )² = 11
(x - 5 ) = ±√11
x = 5 ± √11
Therefore, the value of x for the given quadratic expression is x = 5 ± √11.
To know more about an expression follow
https://brainly.com/question/27826679
#SPJ1
evaluate the expression 2(6w-2y)-8z if w=3/4, y=-2 and z=0.4
Answers
Answer:
13.8
Step-by-step explanation:
2(6(3/4)-2(-2))-8(.4)
2(4.5+4)-3.2
17-3.2= 13.8
