Answers
1c. = 1/2 lb, 1 lb = 4 sticks of butter
Related Questions
1. You spent $10 to buy 5 vases, how much does one vase cost? *
1 point
$1
$2
$5
$50
Answers
Answer:
$2
Step-by-step explanation:
if you divide 10 by 5 you get 2
Answer:
Each vase would cost 2$. 10 divided by 5 is 2 therefore each vase is 2$.
Step-by-step explanation:
every year a laptop is worth 1/3 of what it was worth for each year previous. if you have a $600 laptop, how much is it worth after 15 years?
Answers
The laptop will be worth $0.001286 after 15 years if its worth becomes 1/3 each year.
We can solve this problem by using the formula for geometric sequences,
an = a₁r^(n-1), here in this case, an is the worth of the laptop after n years, r is the rate at which the worth is changing that 1/3 in this case and a₁ is the value of the laptop currently. Substituting the given values, we get:
a₁₅ = 600(1/3)¹⁵⁻¹
a₁₅ = 600(1/3)¹⁴
a₁₅ = 600x0.0000021433
a₁₅ = 0.001286
Therefore, after 15 years, the laptop is worth approximately $0.001286.
To know more about geometric sequence, visit,
https://brainly.com/question/24643676
#SPJ4
Gerard concluded that the triangle with sides feet, 8 feet, and cannot be used as a building frame support on the house because it is not a right triangle. How did gerard come to that conclusion? explain.
Answers
Gerard concluded that triangle with given sides cannot be used as building-frame support because it is not right triangle, he come to this conclusion because the Pythagoras-theorem is not satisfied.
In order to check if a triangle is "right-triangle", Gerard used the Pythagorean theorem. According to this theorem, in right triangle, the square of length of hypotenuse (the side opposite the right angle) is equal to sum of squares of other two sides,
So, the squares of the given sides are :
Square of √95 feet = (√95)² = 95 feet
Square of 8 feet = 8² = 64 feet
Square of √150 feet = (√150)² = 150 feet
We see that, 95 feet + 64 feet = 159 feet ≠ 150 feet,
Since the square of the longest side (√150) is not equal to the sum of the squares of the other two sides (√95 and 8), the Pythagorean-theorem is not satisfied.
Therefore, Gerard concluded that the triangle with sides √95 feet, 8 feet, and √150 feet is not a right triangle.
Learn more about Triangle here
https://brainly.com/question/29119900
#SPJ4
The given question is incomplete, the complete question is
Gerard concluded that the triangle with sides √95 feet, 8 feet, and √150 cannot be used as a building frame support on the house because it is not a right triangle. How did Gerard come to that conclusion? explain.
Consider the following sample data values. 7 4 6 12 8 15 1 9 13 a) Calculate the range. b) Calculate the sample variance. c) Calculate the sample standard deviation. a) The range is 14 b) The sample variance is (Round to two decimal places as needed.) c) The sample standard deviation is (Round to two decimal places as needed.)
Answers
a) The range is 14.
b) The sample variance is 20.78.
c) The sample standard deviation is 4.56.
a) Range
The range of a given set of data values is the difference between the maximum and minimum values in the set. In this case, the maximum value is 15 and the minimum value is 1. So, the range is:
Range = maximum value - minimum value
Range = 15 - 1
Range = 14
b) Sample variance
To calculate the sample variance, follow these steps:
1. Calculate the sample mean (X). To do this, add up all of the data values and divide by the total number of values:
n = 9
∑x = 7 + 4 + 6 + 12 + 8 + 15 + 1 + 9 + 13 = 75
X = ∑x/n = 75/9 = 8.33
2. Subtract the sample mean from each data value, square the result, and add up all of the squares:
(7 - 8.33)² + (4 - 8.33)² + (6 - 8.33)² + (12 - 8.33)² + (8 - 8.33)² + (15 - 8.33)² + (1 - 8.33)² + (9 - 8.33)² + (13 - 8.33)² = 166.23
3. Divide the sum of squares by one less than the total number of values to get the sample variance:
s² = ∑(x - X)²/(n - 1) = 166.23/8 = 20.78
Therefore, the sample variance is 20.78 (rounded to two decimal places).
c) Sample standard deviation
To calculate the sample standard deviation, take the square root of the sample variance:
s = √s² = √20.78 = 4.56
Therefore, the sample standard deviation is 4.56 (rounded to two decimal places).
Learn more about range here: https://brainly.com/question/30339388
#SPJ11
V I’mhjhvcbjvcvjhvvvggujvvcghhhvcccgggghh

Answers
Answer:
the like terms were not grouped together.
A company that makes hair-care products had 5,000 people try a new shampoo. Of the 5,000
people, 35 had a mild allergic reaction. What percent of the people had a mild allergic reaction?
Answers
Mke y the subject of the formula.
w=x^2-2yz

Answers
Answer:
W = x^2 - 2yz / - w
0 = x^2 - 2yz - w / +2yz
2yz = x^2 - w // 2z
y = (x^2 -w ) / 2z
So correct answer is D
4 Stretch Your Thinking: Brian has some boxes of paper clips. Some boxes hold 10 clips and some boxes hold 100. He has some paper clips left over. He has three more boxes with 100 paper clips than he has boxes with 10 paper clips. He has two fewer paper clips left over than he has numbers of boxes with 100 paper clips. What number of paper clips could he have?
Answers
Answer:
Any of {412, 523, 634, 745, 856, 967, 1078, 1189}
Step-by-step explanation:
Relations are given between the number of 10-clip boxes, the number of 100-clip boxes, and the number left over. We assume there are at least one of each size box, and that there are fewer than 10 clips left over. (10 could be put into another box.)
__
Let h represent the number of 100-clip boxes. Then h-3 is the number of 10-clip boxes, and h-2 is the number of clips left over. The total number of paperclips is ...
10(h -3) +100h +(h -2) = 111h -32
In addition, we require ...
h -3 > 0 and h-2 < 10
3 < h < 12 . . . . . . . rearranging these inequalities
So, Brian could have 111h -32 paper clips, where 3 < h < 12. That could be any of {412, 523, 634, 745, 856, 967, 1078, 1189} paper clips.
What is the set of all elements in the universal set that are not in the set a called?
Answers
Complement of set A is the set of all elements in the universal set that are not in the set .
If there is a subset of the universal set (U) called A, then the complement of set A, denoted by the symbol A', is different from the elements of set A and contains the elements of the universal set but not the elements of set A.
In this case, A' = x U: x A.
In other words, the complement of a set A is the difference between the universal set and set A.
For example: U = {1, 2, 3, 5, 7, 9, 15 ,14, 13}, A = {1, 2, 3, 5,7,9}, find the complement of A.
A' = U - A = {1, 2, 3, 5, 7, 9, 15,14,13} - {1, 2, 3, 5,7,9} = {15,14, 13}
A set that contains items from all related sets, without any repetition of elements, is known as a universal set (often symbolised by the letter U). If A and B are two sets, for example, A = 1, 2, 3 and B = 1, a, b, c, then U = 1, 2, 3, a, b, c is the universal set that these two sets belong to.
know more about universal set click here
https://brainly.com/question/8053622
#SPJ4
True or False: Midpoint is represented by a whole number, Indicating a length.
Answers
other things being equal, the width of a confidence interval gets smaller as:__
Answers
Other things being equal, the width of a confidence interval gets smaller as the sample size increases.
The width of a confidence interval gets smaller as:
The sample size increases: As the sample size increases, we have more information about the population, leading to a more precise estimate.The confidence level decreases: The confidence level determines the level of certainty we want to have in our estimate. The variability or standard deviation of the population decreases: When the population variability is low, the data points are closer together, resulting in a more precise estimate.Learn more about Confidence interval here:
https://brainly.com/question/32546207
#SPJ1
HELP!!
GIVING BRAINLIEST!!

Answers
Scores on a standardized test are normally distributed with a mean of 450 and a standard deviation of 35.
Approximately what percent of students scored between 460 and 480?
30%
19%
11%
4%
Answers
The percent of students scored between 460 and 480 is 19%. The Option B.
What percentage of students scored 460 to 480?To get percentage of students who scored between 460 and 480, we need to calculate z-scores for these values and then find the corresponding area under the normal distribution curve.
We will calculate the z-score for 460:
z = (x - μ) / σ
z = (460-450)/35
z = 10/35
z = .2857
P(z < .2857) = 0.6124
P(z < .2857) 61.24%
We will calculate the z-score for 480:
z = (480-450)/35
z = 30/35
z = .8571
P(z < .8571) = .8040
P(z < .8571) 80.40%
The difference between the scores is:
= 80.40% - 61.24%
= 19.16%
Read more about distribution
brainly.com/question/23286309
#SPJ1
estimate the total cost of 31 televisions at £196.50 each and 19 DVD players at £50.99 each
Answers
Answer:
£7060.31Solution,
Cost of one television=£196.50
cost of 31 televisions:
\( = 196.50 \times 31 \\ = 6091.5\)
Cost of one DVD player=£50.99
Cost of 19 DVD player:
\( = 50.99 \times 19 \\ = 968.81\)
Now,
Total cost
= cost of 31 televisions + cost of 19 DVD player
=6091.5+968.81
=£7060.31
Hope this helps...
Good luck on your assignment..
Answer:
£7060.31Step-by-step explanation:
Cost of a television = £196.50cost of 31 televisions.
\(196.50 \times 31 \\ = 6091.5 0\\ \)
Cost of a DVD player = £50.99cost of 19 DVD players
\(50.99 \times 19 \\ = 968.81 \\ \)
Now let's find the total cost
\(6091.50 + 968.81 \\ = 7060.31\)
Evaluate ∫ ∫ (x² + y²)dx dy over the region in the positive quadrant which x+y≤1.
Answers
The given double integral is ∫ ∫ (x² + y²)dx dy, and we need to evaluate it over the region in the positive quadrant where x+y≤1.
To evaluate this double integral, we can first determine the limits of integration for both x and y based on the given region. In the positive quadrant, x and y both range from 0 to 1.
Now, integrating the inner integral with respect to x, we get:
∫ (x² + y²)dx = (1/3)x³ + y²x + C1,
where C1 is the constant of integration.
Next, we integrate the resulting expression with respect to y:
∫ [(1/3)x³ + y²x + C1] dy = (1/3)x³y + (1/3)y³x + C1y + C2,
where C2 is another constant of integration.
Finally, we evaluate this double integral over the given region by substituting the limits of integration:
∫∫ (x² + y²)dx dy = ∫[0 to 1] ∫[0 to 1-x] (x² + y²)dy dx.
Performing the integration, we can find the numerical value of the double integral within the given region.
Learn more about integral here: brainly.com/question/18125359
#SPJ11
If f(x)=2x+7 and g(x)= x^2-4/2x+1 then g(f(-5))?
a)-3
b)6
c)-1
d)2
Answers
Answer:
It should be 2
Step-by-step explanation:
I searched it up
The value of the g(f(-5)) is -1 f(x)=2x+7 and g(x)= x^2-4/2x+1 then g(f(-5)) option (c) is correct.
What is a function?It is defined as a special type of relationship and they have a predefined domain and range according to the function every value in the domain is related to exactly one value in the range.
We have:
f(x) = 2x+7 and
\(\rm g(x) = \frac{x^2-4}{2x+1}\)
First calculating f(-5)
f(-5) = 2(-5) + 7 = -3
Putting x = -3 in the g(x)
\(\rm g(-3) = \frac{-3^2-4}{2(-3)+1}\)
g(-3) = 5/(-5)
g(-3) = -1
Thus, the value of the g(f(-5)) is -1 f(x)=2x+7 and g(x)= x^2-4/2x+1 then g(f(-5)) option (c) is correct.
Learn more about the function here:
brainly.com/question/5245372
#SPJ2
y=x^2-8 is linear or nonlinear
Answers
Answer:
Nonlinear.
Step-by-step explanation:
Slope-Intercept Form: y = mx + b
m - slope
b - y-intercept
We notice that if the line is linear, x will NOT go over a degree of 1.
x² is a quadratic function, and its slope is not proportional like a linear line.
ca group of volunteers were making masks to donate to hospital. They had 25 yards of fabric each mask required 1/8 yard of fabric. how many masks could the group of volunteers make out of 25 yards of fabric
Answers
The group of volunteers can make a total of 200 masks out of 25 yards of fabric.
To calculate the number of masks that can be made, we divide the total amount of fabric (25 yards) by the amount of fabric required per mask (1/8 yard). To do this, we first convert the fraction 1/8 to decimal form, which is 0.125. Then, we divide the total fabric (25 yards) by the fabric required per mask (0.125 yards). This can be done by dividing 25 by 0.125, which equals 200. Therefore, the group of volunteers can make a total of 200 masks out of 25 yards of fabric. Each mask requires 1/8 yard of fabric, so dividing the total fabric by the fabric required per mask gives us the total number of masks that can be made.
Calculation steps:
1. Convert the fraction 1/8 to decimal form: 1/8 = 0.125.
2. Divide the total fabric (25 yards) by the fabric required per mask (0.125 yards):
25 / 0.125 = 200.
To know more about decimal visit:
https://brainly.com/question/2362378
#SPJ11
what are these questions i need help
177
3 is a root of f(x) = x2–93987. Find the other roots of f(x).
Write your answer as a list of simplified values separated by commas, if there is more than one value.
Answers
The roots of the equation f(x) = x^2 - 93987 are x = √93987 and x = -√93987
What are quadratic equations?Quadratic equations are equations that have a second degree and have the standard form of ax^2 + bx + c = 0, where a, b and c are constants and the variable a does not equal 0
How to determine the other roots of the equation?The equation of the function is given as:
f(x) = x^2 - 93987
The above equation is a quadratic equation
Express the equation as a difference of two squares
f(x) = (x - √93987)(x + √93987)
Set the equation of the function to 0
(x - √93987)(x + √93987) = 0
Split the factors of the above function equation as follows
x - √93987 = 0 and x + √93987 = 0
Solve for x in the above equations
x = √93987 and x = -√93987
Hence, the roots of the equation f(x) = x^2 - 93987 are x = √93987 and x = -√93987
Read more about roots of equation at
https://brainly.com/question/776122
#SPJ1
the supervisor of a call center would like to assemble a committe of 8 people from a staff of 15 call center agents. how many diffrent comittes can be chosen
Answers
Supervisor can choose 6435 different such 8 people committees from 15 call center agents.
We know that we can choose ' r ' number elements or persons from ' n ' number of elements or persons respectively in C(n, r) ways if we do not replace once chosen elements.
Here the total number of staff of call center agent is = 15
So n = 15.
And supervisor of the call center has to choose 8 agents from that group of 15 agents.
So, here r = 8.
Here as supervisor chooses a person he or she cannot be selected as two people.
So the event is without replacement.
Thus by the combination formula, the number of different such committees can be chosen by supervisor is = C(15, 8) = 6435.
Hence, supervisor can choose 6435 different such 8 people committees from 15 call center agents.
To know more about combination formula here
https://brainly.com/question/30806372
#SPJ4
Solve for x.
1/4 (x−2/5) = −1 1/2
Enter your answer as a mixed number in simplest form by filling in the boxes.
Answers
Answer:
First, we can simplify the left side of the equation by distributing 1/4:
1/4 (x - 2/5) = 1/4 x - 1/5
Now the equation becomes:
1/4 x - 1/5 = -1 1/2
We can convert the mixed number on the right side to an improper fraction:
-1 1/2 = -3/2
Adding 1/5 to both sides, we get:
1/4 x = -3/2 + 1/5
Combining the fractions on the right side:
1/4 x = -13/10
Multiplying both sides by 4:
x = -13/10 * 4 = -26/5
We can convert this to a mixed number in simplest form by dividing the numerator by the denominator:
x = -5 1/5
Lance has 3 time as many pencils as Nick, and they have 84 pencils together. How many pencils does each of them have?
Answers
Answer:
21 pencils for Nick and 63 pencils for Lance
Step-by-step explanation:
Lance is said to have 3 times the pencils Nick has.Let's keep the number of pencils Nick has as x.If Nick has x pencils that means Lance has 3x pencils. The total number of pencils present is 84.Now let's make an equation out of the information above:
3x + x = 84
Now solve for x.
3x + x = 84
4x = 84
x = 84/4
x = 21
So Nick has 21 pencils
Now for Lance:
3x
3 * (21) = 63
So Lance has 63 pencils
63 + 21 = 84 pencils
You have 24 packets that each have 1/3 ounce of honey for your chicken Mac nuggets. If you ate all of the honey, how much honey would you have eaten?
Answers
Answer:
8 ounces of honey
Step-by-step explanation:
A five feet tall woman is walking towards a 20 feet tall street lamp at a rate of 3ft/s. The distance between her and the street lamp is labeled by x and the length of her shadow which the lamp casts is labeled by y. Answer the following questions about this situation.Which of the following equations represents a relationship between dy/dt and dx/dt ?A. dy/dt = 1/3 *dx/dt B. dy/dt = 3 *dx/dt C. dy/dt = 4*dx/dt D. dy/dt = 1/4 *dx/dt
Answers
The equation representing the relationship between dy/dt and dx/dt that is rate at which the length of the woman's shadow is changing is equal to option C. dy/dt =4× (dx/dt).
Woman is walking towards the street lamp.
Rate at which the length of her shadow is changing as she walks.
Let us consider the height of the street lamp as h = 20 feet.
Height of the woman be w = 5 feet.
And the distance between the woman and the street lamp be x.
Length of the woman's shadow be y.
Triangles formed by the woman, the street lamp, and their shadows are similar.
Sides of similar triangles are in proportion,
This implies,
h / y = (h + w) / (x + y)
Solving for y we get,
⇒h(x + y) = y(h + w)
⇒hx + hy = hy + wy
⇒y = hx / w
Rate at which the length of the woman's shadow is changing by differentiating both sides of this equation with respect to time,
⇒ dy/dt = h(dx/dt) / w
Substitute in the values for dx/dt = 3 ft/s, h and w we get,
⇒dy/dt = (20)(3) / 5
⇒dy/dt = 60 /5
⇒dy/dt =12
⇒dy/dt = 4(3)
⇒dy/dt =4× (dx/dt)
Therefore, the rate at which the length of the woman's shadow is changing is given by option C. dy/dt =4× (dx/dt) .
learn more about length here
brainly.com/question/29292459
#SPJ4
If z=(x+y)e^y and x=3t and y=1- t2, find the following derivative using the chain rule. Enter your answer as a function of t.
dz/dt =
Answers
The derivative dz/dt can be found by applying the chain rule. Let's first substitute the given expressions for x and y into the equation for z:
z = (x + y)e^y
z = (3t + 1 - t^2)e^(1 - t^2)
Now, we can differentiate z with respect to t using the chain rule. The chain rule states that if u = f(g(t)), then du/dt = f'(g(t)) * g'(t).
Applying the chain rule to the given equation, we have:
dz/dt = d((3t + 1 - t^2)e^(1 - t^2))/dt
To differentiate this expression, we need to consider the derivative of each term. Let's break it down:
1. The derivative of 3t with respect to t is simply 3.
2. The derivative of 1 with respect to t is 0 since it is a constant.
3. The derivative of -t^2 with respect to t is -2t.
4. The derivative of e^(1 - t^2) with respect to t can be found using the chain rule again.
For the fourth term, let's define u = 1 - t^2. The derivative of u with respect to t is du/dt = -2t. Now, we have:
dz/dt = (3 + 0 - 2t)e^(1 - t^2) + (3t + 1 - t^2)d(e^(1 - t^2))/dt
Using the chain rule once more, we differentiate e^(1 - t^2) with respect to u:
d(e^(1 - t^2))/du = e^(1 - t^2) * d(1 - t^2)/dt
The derivative of 1 - t^2 with respect to t is -2t. Substituting this back into our expression, we get:
dz/dt = (3 + 0 - 2t)e^(1 - t^2) + (3t + 1 - t^2)(-2t)e^(1 - t^2)
Simplifying the expression, we have:
dz/dt = (3 - 2t)e^(1 - t^2) - 2t(3t + 1 - t^2)e^(1 - t^2)
Therefore, the derivative dz/dt is given by (3 - 2t)e^(1 - t^2) - 2t(3t + 1 - t^2)e^(1 - t^2), where e represents the exponential function.
To learn more about derivatives click here: brainly.com/question/29144258
#SPJ11
93748 x 837482768836334
Answers
Which table represents a linear function?
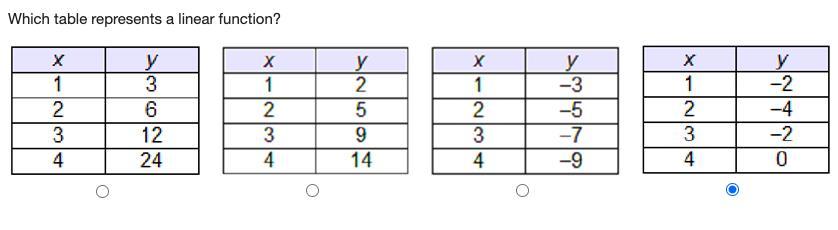
Answers
Answer:
the third one
Step-by-step explanation:
a linear function is information that is increasing or decreasing at a steady rate, in that specific set of data their decreasing at a rate of 2
Cual es el resultado de (3/4)²
Answers
Answer:
Step-by-step explanation:
1. (3/4)^2 = 3/4 * 3/4
2. numerator * numerator so 3 * 3 = 9
3. denominator * denominator so 4 * 4 = 16
Hence, the answer is 9/16
Step-by-step explanation:
(3/4)² = 3²/4² = 9/16
(a×b×c×d×...×z)² = a²×b²×c²×d²×...×z²
Jessie designed a sculpture that is shaped like a circle. The circumference of the sculpture is 10π meters. Which measurement is closest to the area of the sculpture in square meters? 31.4 m² 78.5 m² 62.8 m² 314 m²
Answers
I believe that it is 31.4, but please correct me if I'm wrong.
The required area of the sculpture that is shaped like a circle is \(78.5m^{2}\).
Given that,
Jessie designed a sculpture that is shaped like a circle,
The circumference of the sculpture is 10π meters.
We have to determine,
Which measurement is closest to the area of the sculpture in square meters.
According to the question,
Circumference of the circle = \(2\pi r\)
Where, circumference = \(10\pi\)
Then,
\(10\pi =2\pi r \\\\r = \dfrac{10\pi }{2\pi }\\\\r = 5m\)
Therefore,
Jessie designed a sculpture that is shaped like a circle.
Area of the circle = \(\pi r^{2}\)
Where, r = 5m
Then,
Area of the circle is given by,
\(= \pi r ^{2}\\\\= 3.14 \times (5)^{2}\\\\= 3.14 \times 25\\\\= 78.5m^{2}\)
Hence, The required area of the sculpture that is shaped like a circle is \(78.5m^{2}\).
To know more about Circle click the link given below.
https://brainly.com/question/20908820
How do you solve this?

Answers
Answer:
Everything is being timesed by 6 So 6/1?
Step-by-step explanation:
