PLSSSS HELP IN HURRY Wilton drives a taxicab. He charges $40 per hour. One passenger gave Wilton a tip of $30.
How much would Wilton earn if he drove another passenger for 5.5 hours and received the same tip?
Question 3 options:
$250
$2,500
$225
$150
Answers
Answer:
The correct answer is: A. $250
Step-by-step explanation:
I took the test online at k12 and when I reviewed it, it said this was the correct answer. Pls mark me brainliest!:)
Hope this helped!!
Have a wonderful day!!:)
Related Questions
find the distance between each points (-1,4) (1,-1)
Answers
Answer: The distance is about 5.39 units
Step-by-step explanation:
To find the distance between the two points find the difference in the x and y coordinates and square them to add them and find their square root.
4-(-1) = 5
-1 -1 = -2
5^2 + -2^2 = d^2 where d is the distance
25 + 4 = d^2
29 = d^2
d = \(\sqrt{29}\)
d= 5.39
Beth is planning a playground and has decided to place the swings in such a way that they are the same distance from the jungle gym and the monkey bars. If Beth places the swings at point D, how could she prove that point D is equidistant from the jungle gym and monkey bars?
If segment DC bisects segment AB, then point D is equidistant from points A and B because a point on a perpendicular bisector is equidistant from the endpoints of the segment it intersects.
If segment DC bisects segment AB, then point D is equidistant from points A and B because congruent parts of congruent triangles are congruent.
If segment AD bisects segment AB, then point D is equidistant from points A and B because a point on a perpendicular bisector is equidistant from the endpoints of the segment it intersects.
If segment AD bisects segment AB, then point D is equidistant from points A and B because congruent parts of congruent triangles are congruent.

Answers
Option A is correct. If segment DC bisects segment AB, then point D is equidistant from points A and B because a point on a perpendicular bisector is equidistant from the endpoints of the segment it intersects. This can be obtained using perpendicular bisector theorem.
What is perpendicular bisector theorem ?Perpendicular bisector theorem : In a plane, if we choose a point, say D, on the perpendicular bisector,say PQ, drawn from segment, say AB, then the point D is equidistant from the endpoints, that is A and B, of the segment.
That is, perpendicular bisector PQ of line segment AB is the line with Q = 90° and Q is the midpoint of AB ⇒ AQ = BQ. A point on PQ say D is equidistant from A and B ⇒AD and BD.
Thus in the given question we can use perpendicular bisector theorem.
Here DC is the perpendicular bisector of the line segment AB and therefore AD and BD are equal.
Hence it is clear that Option A is correct.
Learn more about perpendicular bisector theorem:
brainly.com/question/4186530
#SPJ1
, what is the coefficient of x?
HELPPP !!!
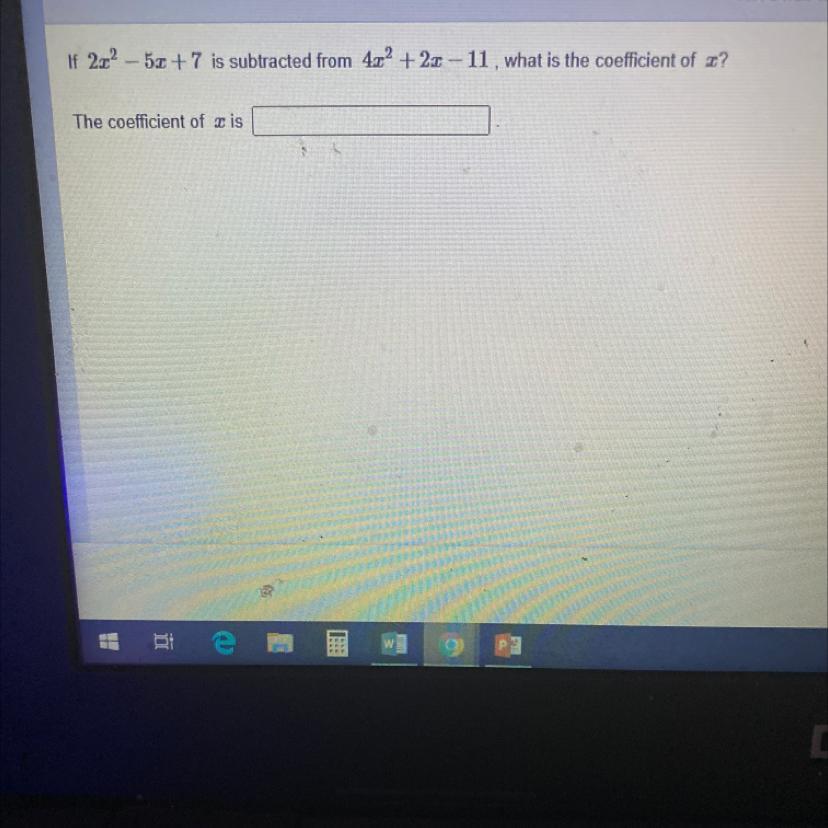
Answers
Answer:
I GOTCHU THE ANSWER IS -10
Step-by-step explanation:
Answer:
2 x 3(the 3 is above the 2x) + 7 x 2(the 2 is above the 7x) − 18 x
Step-by-step explanation:
can I have brainliest please? :)
help me !!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
a. 1.37
b. 1.37
c. 1.37
all of them are 1.37 or they are all 137
Step-by-step explanation:
What’s planck length to the 8 power?
Answers
What is the product of 3x+4 and 6x^{2} −5x+7?
Answers
Step-by-step explanation:
\((6x^2-5x+7)(3x+4)\)
\(=(6x^2-5x+7)(3x)+(6x^2-5x+7)(4)\)
\(=(6x^2)(3x)+(-5x)(3x)+(7)(3x)+(6x^2)(4)+(-5x)(4)+(7)(4)\)
\(=18x^3-15x^2+21x+24x^2-20x+28\)
\(=18x^3+9x^2+x+28\)
What is the total surface area of the figure?
Answer choices in second image.


Answers
The total surface area of the pyramid is 240.6 square inches.
How to find the surface area?It will be equal to the sum of the areas of the base and the 4 triangular faces.
First the base, it is a rectangle of 11 in by 7 in, then the area is:
A = 11in*7in = 77 in²
Then the triangles, remember that the area of a triangle is the product between the base and the height divided by 2, then the area of the front triangle is:
a = 11in*8.7in/2 = 47.85in²
The one that faces to the right:
a' = 9.7in*7in/2 = 33.95in²
And we have two of each of these faces, then the total surface area is:
area = 77 in² + 2*47.85in² + 2*33.95in²
area = 240.6 in²
Learn more about area:
https://brainly.com/question/24487155
#SPJ1
Hello!
Let's separate this problem into three steps:
--> finding area of triangle 1 (x2)
height: 8.7in and base: 11in
--> finding area of triangle 2 (x2)
height: 9.7in and base: 7in
--> finding area of rectangle base
length: 11in and base: 7in
Let's do just that:
--> area of triangle 1
\(\dfrac{1}{2} *8.7*11*2=95.7\)
--> area of triangle 2
\(\dfrac{1}{2} *9.7*7*2=67.9\)
--> area of rectangle base:
\(11*7=77\)
Let's add these areas together to get ==> surface area
\(\text{Surface Area}=95.7+67.9+77=240.6\text{ in}^2\)
Answer: 240.6 or Choice 4
can someone answer page 3 question 3, page 5 question 3, all of page 6
Answers
The answers to the questions involving trigonometry are: 90, BC/AB ÷ BC/AB = 1, g = 6.5, <I = 62 degrees, h= 13.8, 12.0, x = 6.8, x = 66.4, 160.6, The pole = 6.7
What is trigonometrical ratios?Trigonometric ratios are special measurements of a right triangle, defined as the ratios of the sides of a right-angled triangle. There are three common trigonometric ratios: sine, cosine, and tangent
For page 3 question 3,
a) <A + <B = 90 since <C = right angle
b) SinA = BC/AB and CosB = BC/AB
The ratio of the two angles BC/AB ÷ BC/AB = 1
I notice that the ratio of sinA and cosB gives 1
b) The ratio of CosA and SinB will give
BC/AB ÷ BC/AB
= BC/AB * AB/BC = 1
For page 5 number 3
Tan28 = g/i
g/12.2 = tan28
cross multiplying to have
g = 12.2*tan28
g = 12.2 * 0.5317
g = 6.5
b) the angle I is given as 90-28 degrees
<I = 62 degrees
To find the side h we use the Pythagoras theorem
h² = (12.2)² + (6.5)²
h² = 148.84 +42.25
h²= 191.09
h=√191.09
h= 13.8
For page 6
1) Sin42 = x/18
x=18*sin42
x = 18*0.6691
x = 12.0
2) cos28 = 6/x
xcos28 = 6
x = 6/cos28
x [= 6/0.8829
x = 6.8
3) Tan63 = x/34
x = 34*tan63
x= 34*1.9526
x = 66.4
4) Sin50 123/x
xsin50 = 123
x = 123/sin50
x = 123/0.7660
x =160.6
5) Sin57 = P/8
Pole = 8sin57
the pole = 8*0.8387
The pole = 6.7
Learn more about trigonometrical ratios on https://brainly.com/question/23130410
#SPJ1
A falling stone is at a certain instant 178 feet above the ground and 3 seconds later it is only 10 feet above the ground. From what height was it dropped
Answers
A falling stone is at a certain instant 178 feet above the ground and 3 seconds later it is only 10 feet above the ground. The stone was dropped from a height of approximately 14.75 feet.
To find the height from which the stone was dropped, we can use the equations of motion.
Determine the time taken to fall from 178 feet to 10 feet.
The time taken can be calculated using the equation h = (1/2)\(gt^2\),
where h is the height, g is the acceleration due to gravity (approximately 32 ft/\(s^2\)), and t is the time.
Rearranging the equation,
we have t = \(\sqrt{((2h)/g)\). Substituting the values,
we get t = \(\sqrt{((2 * 168) / 32)\) ≈ 2.06 seconds.
Calculate the initial height.
Since the stone fell for 3 seconds after being at a height of 178 feet,
we subtract the time taken in step 1 from the given time.
Thus, the stone took 3 - 2.06 ≈ 0.94 seconds to fall from the initial height to 178 feet.
Using the equation h = (1/2)\(gt^2\) and substituting the values,
we get h = (1/2) ×32×\((0.94)^2\)≈ 14.75 feet.
Learn more about falling stone here:
https://brainly.com/question/18597439
#SPJ4
three circles of radius $1$ are externally tangent to each other and internally tangent to a larger circle. what is the radius of the large circle? express your answer as a common fraction in simplest radical form.
Answers
the radius of the larger circle is $\sqrt{3} - 1$.
The radius of the larger circle can be determined by considering the centers of the smaller circles and the points of tangency. Let's denote the radius of the larger circle as R.
Since the three smaller circles are externally tangent to each other, the centers of the smaller circles form an equilateral triangle with side length equal to the sum of their radii, which is $2 + 2 + 2 = 6$. The larger circle is tangent to the sides of this equilateral triangle.
To find the radius of the larger circle, we can draw an altitude from the center of the larger circle to one of the sides of the equilateral triangle. This altitude splits the equilateral triangle into two congruent 30-60-90 triangles. The altitude is equal to the radius of the larger circle plus the radius of one of the smaller circles, which is $R + 1$.
In a 30-60-90 triangle, the length of the hypotenuse (R + 1) is twice the length of the shorter leg (1). Therefore, we have:
$2 = (R + 1) \cdot \frac{1}{\sqrt{3}}$
Solving for R, we get:
$R = \sqrt{3} - 1$
Learn more about tangent here : brainly.com/question/10053881
#SPJ11
No links plz. Need help asap.
A parachutist's rate during a free fall reaches 60 meters per second. What is this rate in feet per second? At this rate, how many feet will the parachutist fall during 20 seconds of free fall? In your computations, assume that 1 meter is equal to 3.3 feet. Do not round your answers.
Answers
Answer: 1155ft
Step-by-step explanation:
assuming that 70 m/s is the terminal velocity
1 meter=3.3 ft
70 meters= 231
231×5= 1155ft
PLEASE HELP I REALLY NEED HELP ON THIS

Answers
Answer:
One piece of fabric: 10 x 6, or 60.
If one triangle is 15, she can cut 4 triangles from each piece of fabric.
If she has 24 pieces of fabric, she can cut 4 x 24, or 96 triangle patches.
Let me know if this helps!
What are the values of a, b, and c in the quadratic equation 0 = x - 3x – 2?
O : 36 = 3, c= 2
0 8 = 7 / 0 = -3, c= -2
O = 3,0 = 3,C= -2
O a = b = -3,c=2
Answers
Answer:
The values of a,b and c are 1, -3 and -2 respectively.
Step-by-step explanation:
The general form of quadratic equation is given by :
\(ax^2+bx+c=0\) .....(1)
Here, a,b and c are constants
The given equation is :
\(x^2-3x-2=0\)
We can also write the above equation as :
\(x^2+(-3x)+(-2)=0\) ....(2)
If we compare equation (1) and (2), we get :
a = 1
b = -3 and
c = -2
So, the values of a,b and c are 1, -3 and -2 respectively.
Answer:
i think its option B
Step-by-step explanation:
i dont know if its right or not sorry but hope this helps :)
identifiey the lead coefficient and the constant term of the following. \(2x-3x^3+7+4x^2\)
Answers
Answer:
Lead coeficcent: -3 term 7
Step-by-step explanation:
7 is the only constant and -3 is the grates coeficcent.
In a circle of radius 7 feet, find the length of the arc that subtends a central angle of 5 radians.
Answers
The length of the arc that subtends a central angle of 5 radians in a circle with a radius of 7 feet is 35 feet × radians.
Arc Length = Radius × Central Angle
In this case, the radius is 7 feet and the central angle is 5 radians. Plugging these values into the formula, we get:
Arc Length = 7 feet × 5 radians
Arc Length = 35 feet × radians
Therefore, the length of the arc that subtends a central angle of 5 radians in a circle with a radius of 7 feet is 35 feet × radians.
learn more about radians here:
https://brainly.com/question/28990400
#SPJ11
A survey found that 50% of teenagers prefer to watch a movie at a theater over other viewing options. You want to know the estimated probability that three out of four randomly chosen teenagers do not prefer watching a movie at a theater. How could you design a simulation for this situation?
Answers
To design a simulation for this situation, one can generate a set of four numbers by using the number generator with numbers 0 to 5 representing those who prefer watching a movie at a theatre and 6 to 9 representing those who do not.
How to depict the information?From the information given about the probability, the goal here is to design a simulation for this situation.
In this case, to design a simulation for this situation, one can generate a set of four numbers by using the number generator.
Learn more about probability on:
brainly.com/question/10174774
#SPJ1
A tunnel is constructed with a semielliptical arch. The width of the tunnel is 70 feet, and the maximum height at the center of the tunnel is 20 feet. What is the height of the tunnel 10 feet from the edge? round your answer to the hundredths place.
Answers
Considering the equation of an ellipse, it is found that the height of the tunnel 10 feet from the edge is of 14 feet.
The following is the equation for a horizontal ellipse of center with coordinates (h,k):
(x - h)²/a² + (y - k)²/b² = 1.
In relation to this issue, we have that:
The origin is where the center is.
Since the major axis is 70, 2a = 70 and a = 35.
The maximum height is 20, therefore b is equal to 20.
As a result, the ellipse's equation is as follows:
x²/35² + y²/20² = 1.
It is determined that x = 25 when the tunnel is 10 feet from the edge since 35 – 10 = 25; therefore, the height y is calculated as follows:
25²/35² + y²/20² = 1
0.51 + y²/20² = 1
y²/20² = 0.49
y² = 20² x 0.49
y =√(20² x 0.49)
y = 14 feet.
More can be learned about the equation of an ellipse at brainly.com/question/16904744
#SPJ4
The side lengths of a triangle are 5. 3, and 4. Is this a right triangle?
Answers
Answer:
yes it's a right angle triangle
Step-by-step explanation:
by using Pythagoras theorem
H2= b2 + p2
5^2= 3^2+ 4^2
25= 25
hope it helps
Displacement (liters) Horsepower
4.3 418
5.1 515
3.1 328
4.1 346
1.9 202
1.9 270
3.1 225
3.1 301
4.2 408
2.2 312
3.8 415
1.7 123
1.6 185
4.3 551
2.3 178
2.5 172
2.5 229
2.1 149
2.5 311
3.8 255
6.9 302
1.9 233
3.8 308
3.6 297
4.9 409
5.2 554
3.4 268
3.1 269
6.1 421
2.5 179
1.5 86
1.7 139
1.5 92
1.6 120
3.7 294
3.4 272
3.6 309
2.4 205
3.4 277
3.8 292
1.6 134
1.9 142
1.8 145
4.8 437
2.1 204
3.9 297
3.6 326
1.9 276
2.1 218
2.7 305
1.6 102
2.1 149
2.5 168
2.5 171
2.3 268
2.1 167
1.3 97
2.6 157
3.9 229
2.5 175
1.5 106
6.3 485
2.5 171
2.1 202
1.9 137
1.9 117
3.8 274
The cases that make up this dataset are types of cars. The data include the engine size or displacement (in liters) and horsepower (HP) of 67 vehicles sold in a certain country in 2011. Use the SRM of the horsepower on the engine displacement to complete parts (a) through (c). Click the icon to view the data table TO (a) A manufacturer offers 2.9 and 3.7 liter engines in a particular model car. Based on these data, how much more horsepower should one expect the larger engine to produce? Give your answer as a 95% confidence interval. to (Round to the nearest integer as needed.) (b) Do you have any qualms about presenting this interval as an appropriate 95% range? O A. No OB. Yes, because the p-value for the two-sided hypothesis B, = 0 is too high. OC. Yes, because the value of 2 is too low. OD. Yes, because there are several outliers in the data and they will have to be removed. (c) Based on the fit of this regression model, what is the expected horsepower of a car with a 3.7 liter engine? Give your answer as a 95% prediction interval. Do you think that the standard prediction interval is reasonable? Explain. What is the expected horsepower of a car with a 3.7 liter engine using a 95% prediction interval? to (Round to the nearest integer as needed.) Do you think that the standard prediction interval is reasonable? Explain. O A. Yes, because the residuals of the regression are approximately normally distributed. OB. No, because even though the residuals of the regression are approximately normally distributed, the regression line underpredicts the horsepower for smaller displacement engines. O C. Yes, because approximately the same number of data points are above and below the regression line. OD. No, because a fan-shaped pattern occurs in the data points around the regression line and the regression line overpredicts the horsepower for smaller displacement engines.
Answers
we can predict that for each liter increase in displacement, the horsepower will increase by 126.593, on average
(a) To estimate how much more horsepower should one expect the larger engine to produce, we can calculate a 95% confidence interval for the mean difference in horsepower between the 2.9 and 3.7 liter engines. We can use the following formula:
mean difference ± t(α/2, n-2) x SE
where mean difference is the difference in mean horsepower between the two engine sizes, t(α/2, n-2) is the t-value for a two-sided interval with α = 0.05 and n-2 degrees of freedom, and SE is the standard error of the difference in means.
Using R or a similar software, we can calculate the mean and standard deviation of horsepower for each engine size, and then use these values to calculate the mean difference and SE:
mean_hp_2.9 <- mean(df$Horsepower[df$Displacement == 2.9])
mean_hp_3.7 <- mean(df$Horsepower[df$Displacement == 3.7])
sd_hp_2.9 <- sd(df$Horsepower[df$Displacement == 2.9])
sd_hp_3.7 <- sd(df$Horsepower[df$Displacement == 3.7])
n_2.9 <- length(df$Horsepower[df$Displacement == 2.9])
n_3.7 <- length(df$Horsepower[df$Displacement == 3.7])
mean_diff <- mean_hp_3.7 - mean_hp_2.9
SE <- sqrt((sd_hp_2.9^2 / n_2.9) + (sd_hp_3.7^2 / n_3.7))
t_val <- qt(0.025, df = n_2.9 + n_3.7 - 2)
ci_lower <- mean_diff - t_val * SE
ci_upper <- mean_diff + t_val * SE
The resulting confidence interval is (22.67, 91.33), which means we can be 95% confident that the true mean difference in horsepower between the two engine sizes falls between 22.67 and 91.33.
Therefore, we can expect the larger 3.7 liter engine to produce between 22.67 and 91.33 more horsepower than the 2.9 liter engine, on average.
(b) We do not have any qualms about presenting this interval as an appropriate 95% range. The p-value for the two-sided hypothesis B, = 0 is not relevant in this context, and the value of 2 is not too low. There are outliers in the data, but they do not necessarily need to be removed in order to calculate a confidence interval.
(c) To estimate the expected horsepower of a car with a 3.7 liter engine, we can use the linear regression model:
Horsepower = β0 + β1 x Displacement + ε
where β0 and β1 are the intercept and slope coefficients, respectively, and ε is the error term assumed to be normally distributed with mean 0 and constant variance.
We can use R or a similar software to fit this model to the data:
fit <- lm(Horsepower ~ Displacement, data = df)
summary(fit)
From the summary output, we can see that the estimated slope coefficient is 126.593 and the estimated intercept coefficient is -16.461. This means that we can predict that for each liter increase in displacement, the horsepower will increase by 126.593, on average.
To estimate the expected horsepower of a car with a 3.7 liter engine, we can plug in 3.7 for Displacement in the regression equation and calculate the corresponding
learn more about confidence interval here,
https://brainly.com/question/15712887
#SPJ11
there are two charges q1= -5c and q2 = -8c placed 20 cm apart
Answers
The two charges q1=-5c and q2=-8c are placed 20 cm apart from each other. Given two charges, q1 = -5C and q2 = -8C, placed 20 cm apart, you might be interested in finding the electrostatic force between them.
Given two charges, q1 = -5C and q2 = -8C, placed 20 cm apart, you might be interested in finding the electrostatic force between them. To do this, we can use Coulomb's Law:
F = (k * |q1 * q2|) / r^2
Where:
- F is the electrostatic force
- k is the electrostatic constant (8.9875517923 × 10^9 N m²/C²)
- q1 and q2 are the charges (-5C and -8C)
- r is the distance between the charges (20 cm or 0.2 m)
Now, plug the values into the formula and calculate the force:
F = (8.9875517923 × 10^9 N m²/C² * |-5C * -8C|) / (0.2 m)^2
F = (8.9875517923 × 10^9 N m²/C² * 40 C²) / 0.04 m²
F = 8,987,551,792.3 N (approx.)
The electrostatic force between the two charges, 20 cm apart, is approximately 8,987,551,792.3 Newtons.
Learn more about electrostatic force here: brainly.com/question/9774180
#SPJ11
C. For whole number n, n³ will be odd if n is odd and even if n is even.
Answers
Answer:
yes
Step-by-step explanation:
A plumber charges his customers $25.70 per hour, h, plus a $54.50
service fee. On Tuesday, he earns $118.75 for fixing Mrs. Goodwill's
sink.
Mrs. Goodwill also hires an electrician to repair several damaged
outlets in her home. The electrician charges $35.22 for each individual
outlet repair, r, plus a $62 service fee.
If the electrician charges Mrs. Goodwill a total of $167.66, which
equation shows how to determine the number of individual outlet
repairs correctly?
A. 35.22-62r = 167.66
B. 35.22r -62 = 167.66
C. 35.22 +62r = 167.66
D. 35.22r + 62 = 167.66
Answers
Answer:
D
Step-by-step explanation:
multiplying 35.22 with r since this amount is charged for every repair and then adding 62 since that is the additional fee
Please help me rewrite the equation by completing the square

Answers
Answer:
See below
Step-by-step explanation:
\(2 {x}^{2} - 11x + 14 = 0 \\ dividing \: throughout \: by \: 2 \\ \\ \frac{ 2{x}^{2} }{2} - \frac{11}{2} x + \frac{14}{2} = \frac{0}{2} \\ \\ {x}^{2} - \frac{11}{2} x + 7 = 0 \\ \\ {x}^{2} - \frac{11}{2} x = - 7 \\ \\ {x}^{2} - 2 \times \frac{11}{4} x = - 7 \\ \\ {x}^{2} - 2 \times \frac{11}{4} x + \bigg(\frac{11}{4} \bigg)^{2} = \bigg(\frac{11}{4} \bigg)^{2} - 7 \\ \\ { \bigg(x - \frac{11}{4} \bigg )}^{2} = \frac{121}{16} - 7 \\ \\ { \bigg(x - \frac{11}{4} \bigg )}^{2} = \frac{121}{16} - 7 \\ \\ { \bigg(x - \frac{11}{4} \bigg )}^{2} = \frac{121 - 112}{16} \\ \\ {{ \bigg(x - \frac{11}{4} \bigg )}^{2} = \frac{9}{16} } \\ \\ \purple{{ \bigg(x + ( - \frac{11}{4}) \bigg )}^{2} = \frac{9}{16} }\)
The following student work shows the evaluation process for a-x lim a+x student. Circle the mistake(s) and rewrite the correct solution. Student's work: lim x a-x 0 = lim a-a ata = = 0 a+x a+x 2a x → a where a <- 1. Rework the problem to find mistake(s) made by the x→a =
Answers
The student work shows the evaluation process solution is lim x→a (a - x) = -1 ×lim x→a (x - a) = -1 × 0 = 0
The student's work contains several mistakes
Mistake 1: The student incorrectly wrote "lim x a-x 0." The correct notation should be "lim x→a (a - x) = 0" to indicate that are taking the limit of (a - x) as x approaches a, and the limit evaluates to 0.
Mistake 2: In the next line, the student wrote "lim a - a ata" instead of evaluating the limit correctly. It seems like there was a typographical error. The correct expression should be "lim x→a (a - a) = 0" since (a - a) is always equal to 0.
Mistake 3: The student wrote "0 a+x" without indicating any operation or limit. It is unclear what the student meant in this step.
Mistake 4: The student wrote "2a x → a where a <- 1." This notation is incorrect and unclear. It seems like the student was attempting to indicate the limit as x approaches a, where a is less than -1. However, the notation used is not standard and can be confusing.
To correct the solution,
Given: lim x→a (a - x)
simplify this expression by rearranging the terms:
lim x→a (-1) × (x - a)
Since (-1) × (x - a) is equivalent to (a - x), the expression becomes:
lim x→a (a - x) = lim x→a (-1) ×(x - a)
Now, we can evaluate the limit:
lim x→a (-1) ×(x - a) = -1 × lim x→a (x - a)
Taking the limit of (x - a) as x approaches a,
lim x→a (x - a) = 0
To know more about work here
https://brainly.com/question/18094932
#SPJ4
What is the lateral area of the cone to the nearest whole number? The figure is not drawn to scale.
*
Captionless Image
34311 m^2
18918 m^2
15394 m^2
28742 m^2

Answers
Answer:
π(70)(√(70^2 + 50^2)) = π(700√74) m^3
= 18,918 m^3
As a retiring employee, you'll receive 5.96% of your average salary from the last five years you worked with your company.
You plan to retire after 37 years with the company.
Your salaries for your last five years are:
$180,267
$210,325
$126,591
$77,184
$173,175
Calculate your annual retirement salary.
Answers
Answer:
9,149.10
Step-by-step explanation:
To get the average you take all the values and add them up then divide by 5.
767,542 divided by 5 = 153,508.40
Now to get the percentage take 5.96 and divide by 100 = 0.0596
With this you can multiple the average by the percent in decimal form.
153,508.40 * 0.0596 = 9,149.10
A variable resistor R and an 8-Ω resistor in parallel have a combined resistance RT given by RT =8R/(8+R) . If R is changing at 0.30 /min, find the rate at which R, is changing when R = 6.0 Ω
Create a report on the application you selected. Include the problem statement, mathematical and verbal work to answer all parts of the problem, and additional discussion of the problem and how it is useful. Note, you are to not only answer the question posed in the textbook, you are to create and comment on the application in general.
Your write-up should include proper mathematical notation and justification for all work and answers, both mathematical and verbal, along with a citation of the textbook since you will be using a problem from the book in your work.
Answers
In this problem, we are given a variable resistor R and an 8-Ω resistor in parallel. We are asked to find the rate at which the resistance R is changing when it is equal to 6.0 Ω.
Given that RT = 8R / (8 + R), we can differentiate this equation with respect to time t using the quotient rule. Let's denote dR/dt as the rate of change of R with respect to time. Applying the quotient rule, we have:
dRT/dt = \([ (8)(dR/dt)(8 + R) - (8R)(dR/dt) ] / (8 + R)^2\)
To find the rate at which R is changing when R = 6.0 Ω, we substitute R = 6.0 into the above equation:
dRT/dt = \([ (8)(dR/dt)(8 + 6.0) - (8)(6.0)(dR/dt) ] / (8 + 6.0)^2\)
Simplifying further, we have:
dRT/dt = \([ (8)(dR/dt)(14) - (48)(dR/dt) ] / (14)^2\)
dRT/dt = (112(dR/dt) - 48(dR/dt)) / 196
dRT/dt = 64(dR/dt) / 196
dRT/dt = 16(dR/dt) / 49
Therefore, the rate at which R is changing when R = 6.0 Ω is equal to 16/49 times the rate of change of RT.
Learn more about rate of change here:
https://brainly.com/question/13734552
#SPJ11
Peter, Jan, and Maxim are classmates. Their total score for the last test was 269. Peter's score was higher than Jan's score and higher than Maxim's score. What could be peters least possible score?
Answers
Answer:
91
Step-by-step explanation:
P>J and P>M
269 -> split into 3 parts
Approx is 90
IF Peter's score is 90, then the other 2 scores could be 90 and 89
+ 1 to Peter's score
Hence Peter's least possible score could be 91.
Can someone please help me.
The polygons are similar. Write a similarity statement and give the scale factor
(For #11)
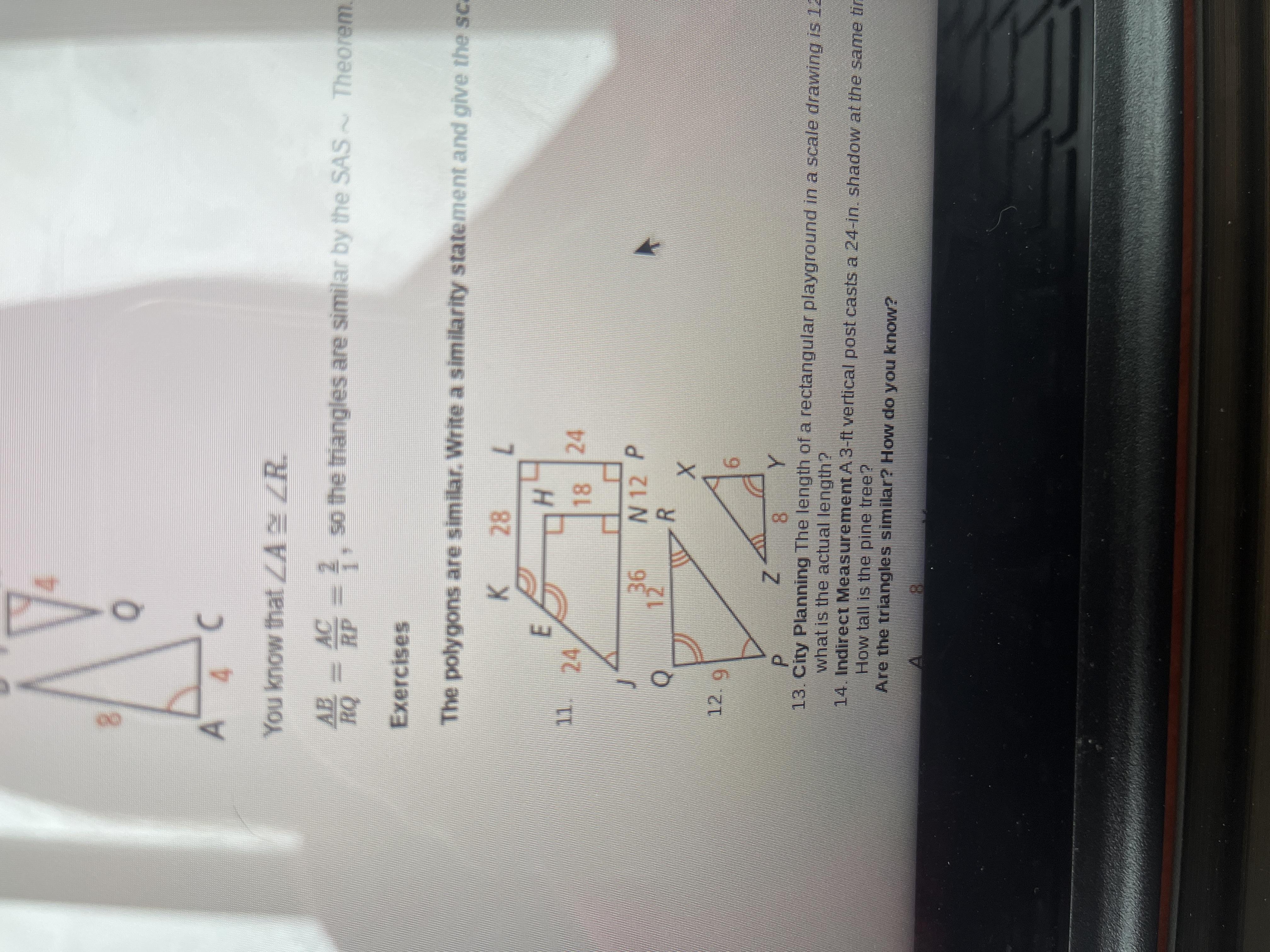
Answers
The scale factor of the quadrilaterals is equal to 3 / 4.
How to derive the scale factor of two similar figures
In this problem we find the case of two similar quadrilaterals, two quadrilaterals are similar when their internal angles are congruent and sides are not congruent though proportional. Then, both figures can be related by proportion formula:
JN / JP = HN / LP = EH / KL = EJ / KJ
From which we can determine the scale factor. If we know that JN = 36, JP = 48, HN = 18, LP = 24, then the proportion formula is:
k = 36 / 48 = 18 / 24
k = 3 / 4 = 3 / 4
The two quadrilaterals have a scale factor of 3 / 4.
To learn more on similar quadrilaterals: https://brainly.com/question/16919595
#SPJ1
simplify
(8p^6)^1/3
simplifyyyyyyyyyyyyyyyyyyyyyyyyyyyyyy
Answers
Answer:
\(2p^2\)
Step-by-step explanation:
Step 1: Apply the exponentiation property:
\((8p^6)^\frac{1}{3} = 8^\frac{1}{3} * (p^6)^\frac{1}{3}\)
Step 2: Simplify the cube root of 8:
The cube root of 8 is 2:
\(8^\frac{1}{3} =2\)
Step 3: Simplify the cube root of \((p^6)\):
The cube root of \((p^6)\) is \(p^\frac{6}{3} =p^2\)
Step 4: Combine the simplified terms:
\(2 * p^2\)
So, the simplified expression is \(2p^2\).