Answers
Answer:
a₈₁ = -1210
Step-by-step explanation:
seq: -10, -25, -40, ...
a = -10 (first term)
d = -25 - (-10) = -15 (difference)
aₙ = a + (n-1)d
a₈₁ = -10 + (81-1)(-15)
= -10 + 80(-15)
= -10 - 1200
a₈₁ = -1210
Answer:
The answer is -1210.
Step-by-step explanation
The common difference in this sequence, -25 - -10= -15
To find the nth term, an= a1+ (n-1)d
Therefore, a81 = -10 + (81-1)(-15) = -1210
Hope this helps
Related Questions
the weight of a small starbucks coffee is a normally distributed random variable with a mean of 420 grams and a standard deviation of 24 grams. find the weight that corresponds to each event. (use excel or appendix c to calculate the z-value. round your final answers to 2 decimal places.)
Answers
The weight of a small Starbucks coffee that is heavier than 480 grams corresponds to a probability of 0.0062.
To find the weight that corresponds to each event, we'll need to use the normal distribution formula:
Z = (X - μ) / σ where Z is the standard score (or z-score), X is the observed value, μ is the mean, and σ is the standard deviation.
We can use this formula to convert the weight of a small Starbucks coffee into a z-score, and then use a standard normal distribution table (such as Appendix C) to find the corresponding probability (or vice versa).
Here are the specific events and their corresponding weights:
1. The weight of a small Starbucks coffee that is lighter than 400 grams. First, we need to convert the weight of 400 grams into a z-score:
Z = (400 - 420) / 24 = -0.83 Using Appendix C or Excel.
we can find that the probability of a z-score being less than -0.83 is 0.2033.
Therefore, the weight of a small Starbucks coffee that is lighter than 400 grams corresponds to a probability of 0.2033.
2. The weight of a small Starbucks coffee that is between 420 and 450 grams. To find the z-scores corresponding to these weights, we need to use the formula twice: For 420 grams: Z = (420 - 420) / 24 = 0 For 450 grams: Z = (450 - 420) / 24 = 1.25 Using Appendix C or Excel, we can find that the probability of a z-score being between 0 and 1.25 is 0.3944.
Therefore, the weight of a small Starbucks coffee that is between 420 and 450 grams corresponds to a probability of 0.3944.
3. The weight of a small Starbucks coffee that is heavier than 480 grams. Again, we need to convert the weight of 480 grams into a z-score:
Z = (480 - 420) / 24 = 2.50 Using Appendix C or Excel, we can find that the probability of a z-score being greater than 2.50 is 0.0062.
Therefore, the weight of a small Starbucks coffee that is heavier than 480 grams corresponds to a probability of 0.0062.
Learn more about standard deviation here,
https://brainly.com/question/31363824
#SPJ4
Plzz answer and thanks

Answers
Answer:
Erosion
Step-by-step explanation:
Erosion is the movement of sediment from one place to another. Erosion is the mechanical process of wearing or grinding somethin down. It condition in which the earth’s surface is worn away by the action of water and wind.
Therefore, the answer is erosion.
If this helps please mark as brainliest
please please please help no one has been able to so far

Answers
The angle of rotation of a conic section is equal to -36 degrees.
How to calculate the angle of rotation of a conic section?Mathematically, the general form of the equation of a conic section is represented or modeled by this mathematical expression:
Ax² + Bxy + Cy² + Dx + Ey + F = 0
Where:
A, B, and C are not all equal to zero.
In Mathematics, the angle of rotation of a conic section can be calculated by using this formula:
Cot(2θ) = [A - C]/B
Where:
θ represents the angle of rotation of a conic section.
From the information provided, we have the following parameters:
3x² - 2√3xy + y² + 2x + 2√3 = 0
A = 3
B = -2√3
C = 1
Substituting the given parameters into the formula, we have;
Cot(2θ) = [3 - 1]/-2√3
Cot(2θ) = -2/2√3
Cot(2θ) = -1/√3
1/tan(2θ) = -1/√3
tan(2θ) = -√3
2θ = tan⁻¹(-√3)
2θ = -71.57
Angle of rotation, θ = -71.57/2
Angle of rotation, θ = -35.79 ≈ -36 degrees.
Note: A negative angle of rotation indicate a counterclockwise rotation.
Read more on angle of rotation here: https://brainly.com/question/12428507
#SPJ1
find the area of the circle shown. the diameter is given.

Answers
Answer:
624.26 m²Step-by-step explanation:
We are given with a circle whose diameter is 28.2 m
Then, Radius will be diameter/2
=> 28.2 /2
=> 14.1 m
Area of circle = πr²
=> 31.4 × (14.1)²
=> 31.4 × 198.81
=> 624.26 m²
Therefore, the area of the given circle is 624.26 m²
Evaluate 11.5x + 10.9y when x = 6 and y =7
Answers
The value of the algebraic expression 11.5x + 10.9y at x = 6 and y = 7 is 145.3
What is an algebraic expression?
Algebraic expression consists of variables and numbers connected with addition, subtraction, multiplication and division
The given algebraic expression is 11.5x + 10.9y
We have to find the value of the algebraic expression at x = 6 and y = 7
Putting x = 6 and y = 7 in the algebraic expression,
\(11.5 \times 6 + 10.9 \times 7\)
69 + 76.3
145.3
To learn more about algebraic expression, refer to the link-
https://brainly.com/question/2164351
#SPJ1
Suppose that the volume of a right circular cylinder is 288 cubic meters and the area of its base is 16 square meters. What is the height of the cylinder?
A. 12 m
B. 16 m
C. 18 m
D. 14 m
Answers
Answer: 18
Step-by-step explanation:
288 / 16 = 18
Answer:
C) 18 m
Step-by-step explanation:
A backpack that normally sells for $39 is on sale for $25. Find the
percent of change.
Answers
Answer: To find the discount, simply multiply the original selling price by the %discount:
ie: 39 x 33/100= $12.87
So, the discount is $12.87.
Step-by-step explanation: To find the sale price, simply minus the discount from the original selling price:
ie: 39- 12. 87= 26.13
So, the sale price is $26.13
Find the solution of the following initial value problem.g'(x)= 3x(x^2 -1/3) ; g(1) = 2
Answers
According to the question we have the solution of the given differential equation initial value problem is: g(x) = (3/4)x^4 - x + 9/4 .
To solve the given initial value problem, we need to integrate both sides of the differential equation. We have:
g'(x) = 3x(x^2 - 1/3)
Integrating both sides with respect to x, we get:
g(x) = ∫[3x(x^2 - 1/3)] dx
g(x) = ∫[3x^3 - 1] dx
g(x) = (3/4)x^4 - x + C
where C is the constant of integration.
To find the value of C, we use the initial condition g(1) = 2. Substituting x = 1 and g(x) = 2 in the above equation, we get:
2 = (3/4)1^4 - 1 + C
2 = 3/4 - 1 + C
C = 9/4
Therefore, the solution of the given initial value problem is:
g(x) = (3/4)x^4 - x + 9/4
In more than 100 words, we can say that the given initial value problem is a first-order differential equation, which can be solved by integrating both sides of the equation. The resulting function is a family of solutions that contain a constant of integration. To find the specific solution that satisfies the initial condition, we use the given value of g(1) = 2 to determine the constant of integration. The resulting solution is unique and satisfies the given differential equation as well as the initial condition.
To know more about differential visit :
https://brainly.com/question/31383100
#SPJ11
Write an expression equivalent to 12+5t−4+15t+1
Answers
Answer:
20t + 9
Step-by-step explanation:
12+5t−4+15t+1
20t + 9
(Simplified version)
Answer:
The answer is 20t+9
Step-by-step explanation:
Which of the following elements of products do firms most frequently have to adapt in order to successfully sell in foreign markets? O brand name labeling/packaging O product positioning O warranties the core product
Answers
Firms most frequently have to adapt their labeling/packaging in order to successfully sell products in foreign markets.
When a company enters a new market, they need to consider the cultural, linguistic, and legal differences that may affect their product packaging and labeling. For example, certain countries may have regulations on the size of text or images on packaging, or certain colors may have different meanings in different cultures.
While all elements of a product may need to be adapted to some extent when entering a foreign market, labeling and packaging are typically the most frequently adapted. This is because these elements are often the most visible and tangible aspects of a product, and can have a significant impact on consumer perception and purchasing decisions. Labeling and packaging must be adapted to fit the cultural norms and preferences of the target market. For example, in some countries, it is customary to include more detailed information about a product's ingredients or manufacturing process on the packaging, while in others, minimalist design is preferred. Additionally, certain countries may require specific information to be included on the packaging, such as warning labels or certifications. Another important consideration is language. If a product is being sold in a market where the primary language is different from the language used on the original packaging, companies may need to translate the packaging and labeling into the local language.
To know more about linguistic visit :-
https://brainly.com/question/780219
#SPJ11
2. a trapezoid has an area of 100 square units. what scale factor would be required to dilate the trapezoid to have each area? 6400 square units
Answers
The scale factor would be 8, that are required to dilate the trapezoid to have each area
The area of a trapezoid can be calculated if the length of its parallel sides and the distance (height) between them are given.
The formula is: A = ½ (a + b) h
where (A) is the area of the trapezoid, 'a' and 'b' are the bases (parallel sides), and 'h' is the height (the perpendicular distance between a and b).
We know that,
The scale factor for the area is found by squaring the scale factor for length.
The ratio of areas is the square root of the length.
6400÷ 100 =64
Scale factor of the trapezoid = √64 =8
So, the scale factor would be 8.
To read more about trapezoids:
brainly.com/question/26687212
#SPJ4
R-1.3 Algorithm A uses 10n log n operations, while algorithm B uses n2 operations. Determine the value n0 such that A is better than B for n ≥ n0.
R-1.4 Repeat the previous problem assuming B uses n √n operations.
I only need R-1.4!!
Answers
For n ≥ 459, Algorithm A is better than Algorithm B when B uses n√n operations.
To determine the value of n₀ for which Algorithm A is better than Algorithm B when B uses n√n operations, we need to find the point at which the number of operations for Algorithm A is less than the number of operations for Algorithm B.
Algorithm A: 10n log n operations
Algorithm B: n√n operations
Let's set up the inequality and solve for n₀:
10n log n < n√n
Dividing both sides by n gives:
10 log n < √n
Squaring both sides to eliminate the square root gives:
100 (log n)² < n
To solve this inequality, we can use trial and error or graph the functions to find the intersection point. After calculating, we find that n₀ is approximately 459. Therefore, For n ≥ 459, Algorithm A is better than Algorithm B when B uses n√n operations.
Learn more about Algorithm here:
https://brainly.com/question/24953880
#SPJ11
R-1.3: For \($n \geq 14$\), Algorithm A is better than Algorithm B when B uses \($n^2$\) operations.
R-1.4: Algorithm A is always better than Algorithm B when B uses \($n\sqrt{n}$\) operations.
R-1.3:
Algorithm A: \($10n \log n$\) operations
Algorithm B: \($n^2$\) operations
We want to determine the value of \($n_0$\) such that Algorithm A is better than Algorithm B for \($n \geq n_0$\).
We need to compare the growth rates:
\($10n \log n < n^2$\)
\($10 \log n < n$\)
\($\log n < \frac{n}{10}$\)
To solve this inequality, we can plot the graphs of \($y = \log n$\) and \($y = \frac{n}{10}$\) and find the point of intersection.
By observing the graphs, we can see that the two functions intersect at \($n \approx 14$\). Therefore, for \($n \geq 14$\), Algorithm A is better than Algorithm B.
R-1.4:
Algorithm A: \($10n \log n$\) operations
Algorithm B: \($n\sqrt{n}$\) operations
We want to determine the value of \($n_0$\) such that Algorithm A is better than Algorithm B for \($n \geq n_0$\).
We need to compare the growth rates:
\($10n \log n < n\sqrt{n}$\)
\($10 \log n < \sqrt{n}$\)
\($(10 \log n)^2 < n$\)
\($100 \log^2 n < n$\)
To solve this inequality, we can use numerical methods or make an approximation. By observing the inequality, we can see that the left-hand side \($(100 \log^2 n)$\) grows much slower than the right-hand side \($(n)$\) for large values of \($n$\).
Therefore, we can approximate that:
\($100 \log^2 n < n$\)
For large values of \($n$\), the left-hand side is negligible compared to the right-hand side. Hence, for \($n \geq 1$\), Algorithm A is better than Algorithm B when B uses \($n\sqrt{n}$\) operations.
So, for R-1.4, the value of \($n_0$\) is 1, meaning Algorithm A is always better than Algorithm B when B uses \($n\sqrt{n}$\) operations.
To know more about Algorithm, refer here:
https://brainly.com/question/28724722
#SPJ4

I need to match each equation with the right answers and I need to show my work for each one
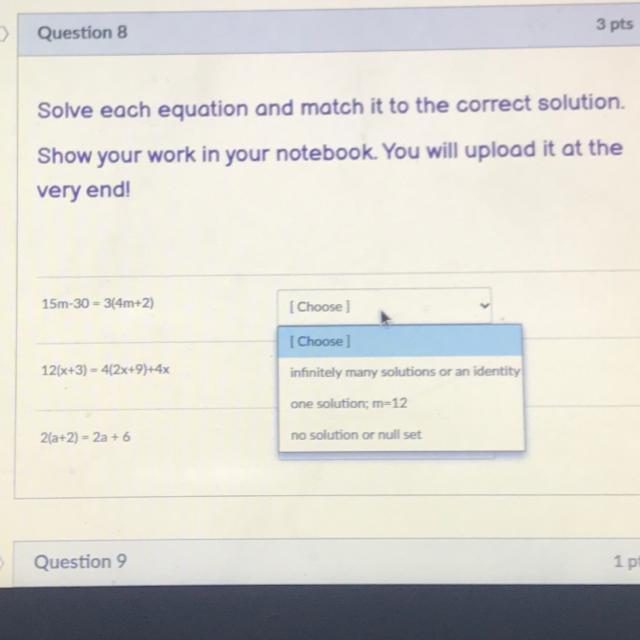
Answers

Need help thx will give Brainiest

Answers
Answer:
it would be 130 aka C
Step-by-step explanation:
i got it right :)
Use the distributive property to write an equivalent expression. 2(m + 9)
Answers
Answer:
Distribute the numbers answer: 2m+18
Step-by-step explanation:
2(m+9)
MULTIPLY 2 and m, and MULTIPLY 2 and 9!
simplify the square root of 272
Answers
PLSS HELP ME! <3
The correct answer will get brainliest and the wrong answer will be reported!
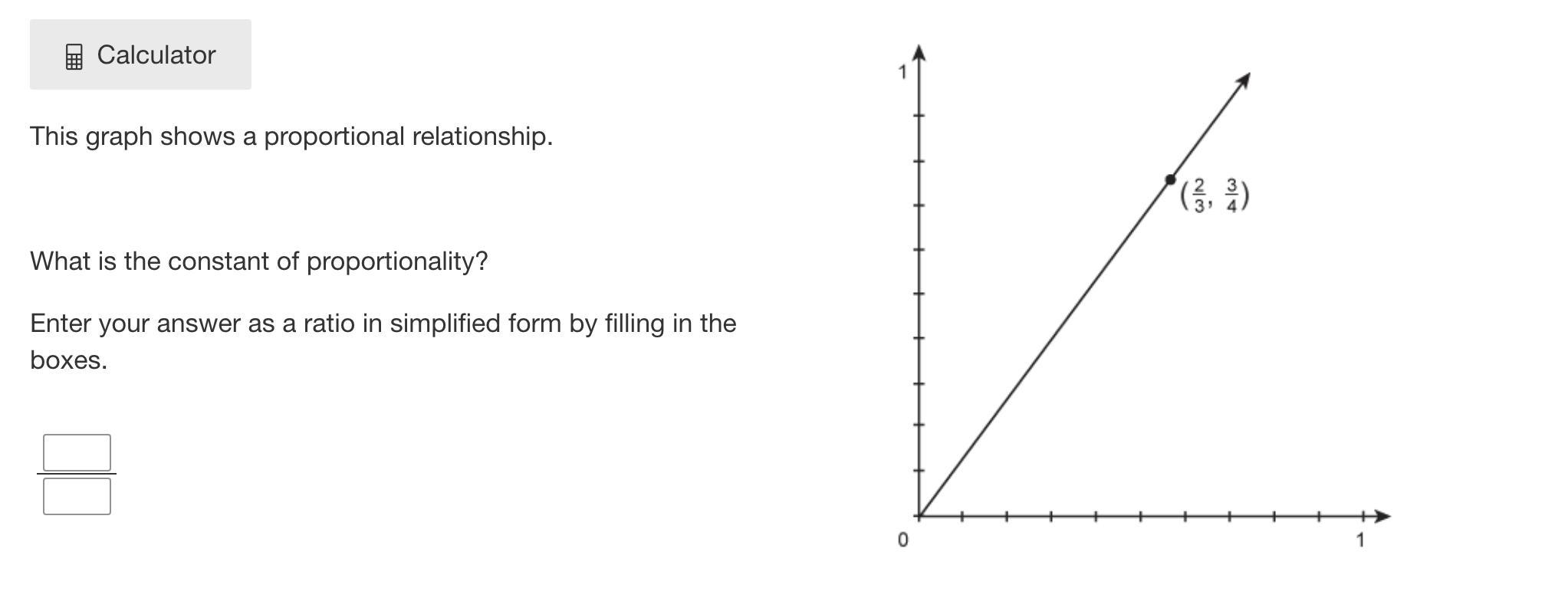
Answers
Answer:
8:9
Step-by-step explanation:
enter
9
-----
8
The first law of thermodynamics states that ΔE= Q− W. Is this also a statement of the principle of conservation of energy? No, the heat that is added to the system is only used to do work. No, the change in internal energy is the energy lost in the system. Yes, the heat added and the change in internal energy of the gas equal the work done by the piston. Yes, the heat that flows into the system is used to change the internal energy of the gas and becomes work done by the piston.
Answers
Answer:
yes
Step-by-step explanation:
as we see in the picture the variation of the internal energy of a system is W-Q by analogie we get the second relation in the 2nd picture wich is the first law of thermodynamics



Answer:
Yes, the heat that flows into the system is used to change the internal energy of the gas and becomes work done by the piston.
Step-by-step explanation:
I took the K12 test :)
determine whether the random variable x is discrete or continuous. explain. let x represent the amount of rain that fell in spring
Answers
The random variable x, which represents the amount of rain (in inches) that fell this spring, is a continuous random variable.
In this context, a continuous random variable is one that can take on any value within a certain range. The amount of rain can be measured with different levels of precision, such as 2.5 inches or 2.5342 inches, indicating that there is an infinite number of possible values between any two given points.
On the other hand, a discrete random variable would involve countable outcomes or a finite number of possible values. For example, if we were counting the number of rainy days during the spring, the random variable would be discrete since it can only take whole number values.
In the case of measuring the amount of rain, there can be infinitely many possible values within any given range, and therefore, it is considered a continuous random variable. So, the correct answer is option A.
Learn more about variable here:
https://brainly.com/question/28248724
#SPJ11
The complete question is:
Decide whether the random variable x is discrete or continuous. Explain your reasoning Let x represent the amount of rain (in inches) that fell this spring. Is the random variable x discrete or continuous? Choose the correct answer below.
A. Continuous, because x is a random variable that cannot be counted.
B. Discrete, because x is a random variable that can be counted.
If the purchase price for a house is $555,750, what is the monthly payment if you put 10% down for a 30 year loan with a fixed rate of 7.947
P= PV-
P= PV
1-(1+0)
O $3,740.19
O $3,327.68
O $2.314.84
O $2.249.10
Answers
The monthly payment if you put 10% down for a 30 year loan with a fixed rate of 7.947 is Option A
How to find the monthly paymentUsing the formula for calculating the monthly mortgage payment:
P = PV / (1 - (1 + r)^(-n))
Where:
P = Monthly payment
PV = Loan amount (purchase price - down payment)
r = Monthly interest rate (annual interest rate divided by 12)
n = Total number of monthly payments (30 years = 30 * 12 = 360)
First, calculate the loan amount (PV):
PV = $555,750 - (10% of $555,750)
PV = $555,750 - $55,575
PV = $500,175
Next, calculate the monthly interest rate (r):
r = 7.947% / 12
r = 0.66225%
Finally, calculate the monthly payment (P):
P = $500,175 / (1 - (1 + 0.0066225)^(-360))
The monthly payment is approximately $3,740.19.
Learn more about mortgage payment at https://brainly.com/question/30093812
#SPJ1
10. A box contains five and two-thirds cups of rice. If three fourths of the rice will
be used, how many cups of rice remained in the box?
14
D.
Answers
Therefore, after using three-fourths of the rice in the box, 4 and 1/4 cups of rice remained.
To find the number of cups of rice that remained in the box, we need to calculate three-fourths (3/4) of the total amount of rice in the box.
The total amount of rice in the box is given as five and two-thirds cups. To work with a fraction, we can convert the mixed number to an improper fraction:
5 and 2/3 = (5 * 3 + 2) / 3 = 17/3 cups
Now, we can find three-fourths (3/4) of 17/3:
(3/4) * (17/3) = (3 * 17) / (4 * 3) = 51/12 = 4 and 3/12 = 4 and 1/4 cups
Therefore, after using three-fourths of the rice in the box, 4 and 1/4 cups of rice remained.
Learn more about three-fourths here
https://brainly.com/question/16953584
#SPJ11
It takes 20 minutes for Maria to read 14 pages in her novel. how many pages can she read in 45 minutes?
Answers
Answer:
32
Step-by-step explanation:
the midpoints of the sides of a regular hexagon abcdef are joined in order to form a smaller regular hexagon. what fraction of the area of abcdef is enclosed by the smaller hexagon?
Answers
A regular hexagon can be divided into six equilateral triangles by drawing lines from the center of the hexagon to each of its vertices.
Each of these equilateral triangles has an area that is one-sixth of the total area of the regular hexagon.
When the midpoints of the sides of the regular hexagon are joined to form a smaller regular hexagon, it can be seen that the smaller hexagon is made up of six equilateral triangles, each of which has half the area of the equilateral triangles in the larger hexagon. This is because the sides of the smaller hexagon are half the length of the sides of the larger hexagon.
Therefore, the fraction of the area of the larger hexagon that is enclosed by the smaller hexagon is:
\(6 * (1/2)^2 = 6 * 1/4 = 3/2\)
This means that the smaller hexagon encloses 3/2 of the area of the larger hexagon.
Learn more about hexagon :
https://brainly.com/question/3295271
#SPJ4

On the freeway it is unsafe to drive too slowly or two quick the safest driving speeds on the freeway near Allentown worst scientifically determined to be between the minimum and maximum speed in miles per hour according to the equation X -55 in value equals 4. 2 which equation can be used to determine the maximum safe driving speed
Answers
|x - 55| is the equation which can be used to determine the maximum safe driving speed.
What is safe driving speed?A safe speed is one that is lower than the peak speed at which the driver can stop within an acceptable amount of time given the current circumstances and conditions and avoid collision.
|x - 55| = 4.2 means that
x - 55 = 4.2 or x - 55 = -4.2
x = 4.2 + 55 or x = -4.2 + 55
x = 4.2 + 55 or x = -4.2 + 55
To know more about safe driving speed please visit:
https://brainly.com/question/13174567
#SPJ4
Find the t-coordinates of all critical points of the given function. Determine whether each critical point is a relative maximum, minimum, or neither by first applying the second derivative test, and, if the test fails, by some other method.
f(t) = −2t3 + 3t
f has ---Select--- a relative maximum a relative minimum no relative extrema at the critical point t =
. (smaller t-value)
f has ---Select--- a relative maximum a relative minimum no relative extrema at the critical point t =
. (larger t-value)
Answers
F has a relative maximum at the critical point t = √(1/2) and a relative minimum at the critical point t = -√(1/2).
A function f has critical points wherever f '(x) = 0 or does not exist.
These points can be either relative maximum or minimum or an inflection point. The second derivative test is a method used to determine whether a critical point is a relative maximum or minimum or an inflection point.
The second derivative test requires that f '(x) = 0 and f "(x) < 0 for a relative maximum and f "(x) > 0 for a relative minimum. In the given function f(t) = −2t³ + 3t,
we need to find the t-coordinates of all the critical points.
We can find these critical points by computing the derivative of f(t).f'(t) = -6t² + 3On equating the derivative to zero,
we get,-6t² + 3 = 0=> t = ±√(1/2)The critical points are ±√(1/2).
Now, we can apply the second derivative test to determine whether these points are relative maxima, minima or neither. f "(t) = -12tAs t = √(1/2), f "(t) = -12(√(1/2)) < 0
Therefore, t = √(1/2) is a relative maximum. f "(t) = -12tAs t = -√(1/2), f "(t) = -12(-√(1/2)) > 0
Therefore, t = -√(1/2) is a relative minimum.
To know more about critical point visit:
https://brainly.com/question/32077588
#SPJ11
Brack, breaks his leash when Mr. Chew is walking him when he sees a rabbit in the woods during their
evening walk. If the puppy runs in straight lines 5 miles west of Mr. Chew and then 7 miles north, how
far from Mr. Chew was Brack, to the nearest tenth of a mile, when he caught the rabbit? Choose the
best answer.
c = 73 miles
c = 8.5 miles
c = 8.54 miles
c = 4.98 miles
Answers
Answer:
8.6 which is closes to c=8.5
Step-by-step explanation:
*See Photo*

The distance between Mr. Chew and Puppy is 8.54 miles. Therefore, option C is the correct answer.
What is the Pythagoras theorem?The Pythagoras theorem which is also referred to as the Pythagorean theorem explains the relationship between the three sides of a right-angled triangle. According to the Pythagoras theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides of a triangle.
Given that, the puppy runs in straight lines 5 miles west of Mr. Chew and then 7 miles north.
Let the distance between Mr. Chew and Puppy be x
Using Pythagoras theorem, we get
x²=5²+7²
x²=74
x=√74
x= 8.54 miles
Therefore, option C is the correct answer.
To learn more about the Pythagoras theorem visit:
brainly.com/question/21926466.
#SPJ1
Three pumpkins are catapulted at a contest. How much farther does Pumpkin C travel than Pumpkin A? • Pumpkin A travels 0.61 mile. • Pumpkin B travels 0.28 mile farther than Pumpkin A. • Pumpkin B travels 0.06 mile farther than Pumpkin C.
Answers
Answer:
0.22 miles
Step-by-step explanation:
Let
A = Distance pumpkin A travels = 0.61 miles
Distance pumpkin B travels is 0.28 mile farther than Pumpkin A
\(B=0.28+A\\\Rightarrow B=0.28+0.61\\\Rightarrow B=0.89\ \text{miles}\)
Distance pumpkin B travels is 0.06 miles further than pumpkin C
\(B=0.06+C\\\Rightarrow C=B-0.06\\\Rightarrow C=0.89-0.06\\\Rightarrow C=0.83\ \text{miles}\)
To calculate how much farther pumpkin C travels than pumpkin A we have the subtract their distances
\(C-A=0.83-0.61=0.22\ \text{miles}\)
So, pumpkin C traveled 0.22 miles more than pumpkin A.
A ladder 25 feet long is leaning against the wall of a house. The base of the ladder is pulled away from the wall at a rate of 2 feet per second.What is the velocity of the top of the ladder when the base is given below?ALREADY KNOWO 7 feet away from the wall= -7/12O 15 feet away from the wall=-3/2O 20 feet away from the wall=-8/3
Answers
The velocity of the top of the ladder is 20.62 feet per second.
We can use the Pythagorean theorem to relate the distance between the wall and the base of the ladder to the height of the ladder. Let h be the height of the ladder, then we have:
h² + 7² = 25²
h² = 576
h = 24 feet
We can then use the chain rule to find the velocity of the top of the ladder. Let v be the velocity of the base of the ladder, then we have:
h² + (dx/dt)² = 25²
2h (dh/dt) + 2(dx/dt)(d²x/dt²) = 0
Simplifying and plugging in h = 24 and dx/dt = -2, we get:
(24)(dh/dt) - 2(d²x/dt²) = 0
Solving for (d²x/dt²), we get:
(d²x/dt²) = (12)(dh/dt)
We can find (dh/dt) using the Pythagorean theorem and the fact that the ladder is sliding down the wall at a rate of 2 feet per second:
h² + (dx/dt)² = 25²
2h(dh/dt) + 2(dx/dt)(d²x/dt²) = 0
Substituting h = 24, dx/dt = -2, and solving for (dh/dt), we get:
(dh/dt) = -15/8
Finally, we can find (d²x/dt²) by plugging in (dh/dt) and solving:
(d²x/dt²) = (12)(dh/dt) = (12)(-15/8) = -45/2
Therefore, the velocity of the top of the ladder is 20.62 feet per second.
Learn more about Pythagorean theorem here: brainly.com/question/28361847
#SPJ4
please help i will give brainliest

Answers
Answer:
y=2x-5 and y=3-2x
Step-by-step explanation:
The inverse of a conditional statement is "If a number is negative, then it has a negative cube root."
What is the contrapositive of the original conditional statement?
If a number is negative, then it does not have a negative cube root.
O If a number does not have a negative cube root, then the number is not negative.
O If a number has a negative cube root, then the number is negative.
O If a number is not negative, then it does not have a negative cube root.

Answers
Answer:
C. If a number has a negative cube root, then the number is negative.
Step-by-step explanation:
took the quiz
The inverse of the conditional statement is " If a number does not have a negative cube root, then the number is not negative. "
What is a conditional statement?A conditional statement is a type of logical statement that expresses a relationship between two propositions or statements. It typically takes the form "if p, then q" where p and q are propositions. The statement "if p, then q" is read as "if p is true, then q is true" or "p implies q".
The truth value of a conditional statement depends on the truth values of its antecedent (p) and its consequent (q). If p is true and q is true, then the conditional statement is true. If p is true and q is false, then the conditional statement is false. If p is false, then the truth value of the conditional statement is irrelevant and it is said to be vacuously true.
Given data ,
Let the statement be represented as A
Now , the inverse of the statement is A'
where A = "If a number is negative, then it has a negative cube root."
Now , the inverse of the conditional statement is
A' = " If a number does not have a negative cube root, then the number is not negative. "
Hence , the inverse is " If a number does not have a negative cube root, then the number is not negative. "
To learn more about conditional statements click :
https://brainly.com/question/18152035
#SPJ7
