PLS HELP QUICK!!!
Solve the system of equations by elimination
3x + 4y=31
2x - 4y=-6
(4, 5)
(5, 4)
(-5. 12.5)
(5, -4)
Answers
===========================================================
Explanation:
Note the matching 4y terms in each equation. The top 4y adds with the -4y down below to get 4y+(-4y) = 0y = 0. This tells us that the y terms go away entirely.
The x terms add to 3x+2x = 5x
The constants on the right hand sides add to 31+(-6) = 25
After adding the equations straight down, we end up with this new equation of 5x = 25
Dividing both sides by 5 leads to x = 5
The answer so far is between B and D.
----------------------------
Let's use this x value to find y
Plugging x = 5 into the first equation leads to...
3x+4y = 31
3(5) + 4y = 31
15 + 4y = 31
4y = 31-15
4y = 16
y = 16/4
y = 4
Or you could use the second equation
2x - 4y = -6
2(5) - 4y = -6
10 - 4y = -6
-4y = -6-10
-4y = -16
y = -16/(-4)
y = 4
Either way, we get the same y value when x = 5.
So x = 5 and y = 4 pair up together.
Overall, the solution is (x,y) = (5, 4)
Related Questions
A puppy named lucky started out at 2 pounds and gained 6 pounds every month. At how many months did lucky weigh 26 pounds
Answers
Answer:
4 months
Step-by-step explanation:
6x+2=26
(6x4)+2=26
x=4
La necesito por favor

Answers
Answer:
4(h+3) = 20
Step-by-step explanation:
Para empesar, disculpa si mi español no es perfecto, pero igual me encataria a ayudarte.
Pues, se sabe que estas temporadas de practica vienen en groupitos de horas a la ves. Dijo que cada dia, ella practica por alguans horas, las cuales suman a 20 en total. Como la problema nos dice que ella practica 4 veces a la semana, tienemos 4 de estos groupitos de horas. Por eso, la respuesa es 4(h+3) = 20, porque ella va por estas 4 temporadas de practicar 3 horas en la manana y quien sabe cuantos en la tarde. Addicionalmente, este"quien sabe" numero de horas se representa con h.
the length of a rectangle pools 15m greater than its width. what is the length if the perimeter of the pool is 96m
Answers
Answer:
31.5 m
Step-by-step explanation:
Let w represent the width of the pool.
Since the length is 15 m greater than the width, it can be represented by w + 15.
Use the perimeter formula, p = 2l + 2w. Plug in the perimeter, and w + 15 as l into the formula:
p = 2l + 2w
96 = 2(w + 15) + 2w
96 = 2w + 30 + 2w
96 = 4w + 30
66 = 4w
16.5 = w
So, the width of the pool is 16.5 m. Add 15 to this to find the length:
16.5 + 15
= 31.5
The length of the pool is 31.5 m
Let the width be w
Length = w + 15
Now
Perimeter = 2(l + w)
96 = 2(w + 15 + w)
96/2 = w + 15 + w
48 = 2w + 15
48 - 15 = 2w
33 = 2w
33/2 = w
16.5 = w
Then,
Length = w + 15
Length = 16.5 + 15
Length = 31.5 m
\( \\ \)
Is 5 1/2 rational or irrational ?
Answers
Answer:
Rational
Step-by-step explanation:
It is a rational number because any number that can be rewritten as a simple fraction is a rational number. This means that natural/counting numbers, whole numbers and integers, like 5, are all part of the set of rational numbers as well because they can be written as fractions, as are mixed numbers such as 1 ½.
Please help the answer options are
1 mph
1 hour per mile
2mph
2 hours per mile

Answers
Answer:
I am positve it 2mph
Step-by-step explanation:
becuase for evry hr u drive 2 miles
Indra completed 80% of her test questions. If there were 120 questions, how many questions she complete
Answers
Answer:
96 questions
Step-by-step explanation:
Given that:
Total number of questions = 120
Percentage questions completed = 80%
Number of questions completed =?
Number of questions completed = total number of questions * percentage questions completed
Number of questions completed = 120 * 0.8
Number of questions completed = 96
Find the distance between points (6, 16) and (-1, 14)
Answers
\( = \sqrt{( {x2 - x1})^{2} + ( {y2 - y1})^{2} } \\ = \sqrt{ (- 1 - 6 )^{2} + ( {14 - 16)}^{2} } \\ = \sqrt{( { - 7)}^{2} + ( { - 2)}^{2} } \\ = \sqrt{49 + 4} \\ = \sqrt{53} \)
ATTACHED IS THE SOLUTION
(1) Area: 35 y² +13y-12
Answers
Answer:
35y2+13y−12
=35y2+28y−15y−12
=7y(5y+4)−3(5y+4)
=(7y−3)(5y+4)
Therefore, the possible length and breadth are 7y-3 units and 5y+4 units
To indirectly measure the distance across a lake, Dominic makes use of a couple landmarks at points � B and � C. He measures � � AD, � � DB, and � � DE as marked. Find the distance across the lake ( � � ) (BC), rounding your answer to the nearest hundredth of a meter.
Answers
The distance across the lake is 190m. Rounding to the nearest hundredth of a meter, the answer is 190.00m.
We can use similar triangles to find the distance across the lake (DE). Since triangle CGF is similar to triangle CED, we can use ratios of the sides to find DE.
Let's call DE = x. Then, we have:
CE/FG = x/142.1
Solving for x, we have:
x = (CE * 142.1) / FG
CE = CF + FD = 130 + 60 = 190m
x = (190 * 142.1) / 142.1 = 190m
The distance across the lake is 190m. Rounding to the nearest hundredth of a meter, the answer is 190.00m.
Learn more about triangles :
https://brainly.com/question/14366937
#SPJ4
The complete question is :
To indirectly measure the distance across a lake, Dominic makes use of a couple landmarks at points D and E. She measures CF, FD, and FG as marked. Find the distance across the lake (DE), rounding your answer to the nearest hundredth of a meter.

two cards are selected in a sequence from a standard deck. what is the probability that the second card is a jack given that the first card was a 2. (assume the 2 was not replaced.)
Answers
The probability that the second card is a jack given that the first card was a 2 is 52/51.
To calculate the probability that the second card is a jack given that the first card was a 2, we need to consider the remaining cards in the deck after the first card is drawn.
When the first card is drawn and it is a 2, there are 51 cards remaining in the deck, out of which there are 4 jacks.
The probability of drawing a jack as the second card, given that the first card was a 2, can be calculated using conditional probability:
P(Second card is a jack | First card is a 2) = P(Second card is a jack and First card is a 2) / P(First card is a 2)
Since the first card is already known to be a 2, the probability of the second card being a jack and the first card being a 2 is simply the probability of drawing a jack from the remaining 51 cards, which is 4/51.
The probability of the first card being a 2 is simply the probability of drawing a 2 from the initial deck, which is 4/52.
P(Second card is a jack | First card is a 2) = (4/51) / (4/52)
Simplifying the expression:
P(Second card is a jack | First card is a 2) = (4/51) * (52/4)
P(Second card is a jack | First card is a 2) = 52/51
To learn more about probability click here:
brainly.com/question/30736116
#SPJ11
Be a kind soul and help me out please

Answers
well, for the piece-wise function, we know that hmmm x = -1, -1 is less 1, so the subfunction that'd apply to that will be -2x + 1, because on that section "x is less than or equals to 1".
so f(-1) => -2(-1) + 1 => 3.
Answer:3
Step-by-step explanation:
In this case x=-1 so you will use the top equation because x<1
so f(-1) = -2(-1) + 1
= 2+1
=3
(THREE CAPITAL LETTERS FOR EACH) ANSWER CORRECTLY !!!!! WILL MARK BRIANLIEST !!!!!! URGENT !!!!!!!!!!

Answers
A student graphs the functions f(x) = | x+3 | and g(x) = x2-2x+3 on the coordinate plane shown.
Which are the solutions of f(x) =g(x)?
A. -3 and 1
B. -1 and 1
C. 0 and 3
D. 3 and 6

Answers
The solutions are the intersection point of both graphs
The left side graph is y=|x+3|The right side top graph is x²-2x+3(Parabola)So there mUST be two solutions
The intersections are
(0,3)(3,6)The x values are solution
They are 0,3Option C
Answer:
C. 0 and 3
Step-by-step explanation:
The solutions of f(x) = g(x) are the values of the x-coordinates of the points where the two graphed functions intersect.
From inspection of the graph, the points of intersection are:
(0, 3)(3, 6)Therefore, the solutions are 0 and 3 (since they are the x-values).
Proof
\(\implies f(x) = g(x)\)
\(\implies |x + 3| = x^2-2x+3\)
We only need to take the positive form of |x+3| since we can see from the graph that g(x) intersects f(x) when |x+3| is positive:
\(\implies x + 3 = x^2-2x+3\)
\(\implies x^2-3x=0\)
\(\implies x(x-3)=0\)
\(\implies x=0, 3\)
Thus confirming that the solutions are when x = 0 and 3
What is the distance between the two points shown on the coordinate plane below?
(-8,-6) to (8,-6)
48 units
12 units
14 units
16 units
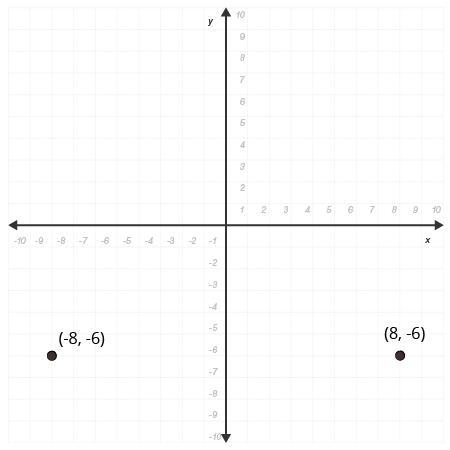
Answers
Answer:
16
Step-by-step explanation:
16
Translate. Eight less than the difference of a number and five is twelve.
Answers
Answer:
(x - 5) - 8 = 12
Step-by-step explanation:
Lets portion each part out:
Eight less than
The difference of a number and five
Is twelve.
First, we must write down the portion with "a number" in it: x - 5. We use subtraction because the sentence states "the difference".
Next, we will write down "eight less than". The problem states that twelve is "eight less than" the difference. This means that we must subtract 8 from out first part: (x - 5) - 8
Finally, the sentence tells us that this equals twelve: (x - 5) - 8 = 12
A sequence is represented by the explicit formula and A sequence is represented by the recursive formula below:
What is the sequence represented by the formula? please help with these two questions it for a test


Answers
Answer:
Answer:
Option C is correct.
Explanation:
Explicit formula for the geometric sequence is given by:
where r is the common ratio term.
Given the recursive formula for geometric sequence:
For n =2
⇒
For n =3
⇒
Common ratio(r):
and so on..
⇒ r = 3
Therefore, the explicit formula for the geometric sequence represented by the recursive formula is:
Step-by-step explanation:
WILL GIVE BRAINLIEST!!!!!!!
2(x+1)^2=12
Answers
Answer:
Step-by-step explanation:

help asap
solve them all i will mark u brainllest





Answers
Answer: (15) see below (16) 284 (17) option 1 (18) option 3
(19) see below (20) 33 (21) L = 50, w = 10
Step-by-step explanation:
15) 7xy + 3x + 5
↓ ↓ ↓
↓ ↓ 5 is a term with no variable so is a constant
↓ 3x is a term with a coefficient of 3
7xy is a term with a coefficient of 7
Constant Coefficient Term
7 X
3x X
5 X X
16) 12a² - 3 |b| + 2a ; a = -5, b = -2
12(-5)² - 3 |-2| + 2(-5)
= 12(25) - 3(2) - 10
= 300 - 6 - 10
= 294 - 10
= 284
17) 4(k + 5) = -2(9k - 4)
4k + 20 = -18k + 8 Distributed 4 and -2
22k + 20 = 8 Added 18k to both sides
22k = -12 Subtracted 20 from both sides
k = -12/22 Divided 21 from both sides
k = -6/11 Simplified (GCF = 2)
18) V = π r²h
V/(π r²) = h Divided π r² from both sides
19) v = s² + (1/2)sh
v - s² = (1/2)sh Subtracted s² from both sides
2(v - s²) = sh Multiplied both sides by 2
2(v - s²)/s = h Divided s from both sides
1 2 3
subtract s² X
divide by s X
multiply by 2 X
20) F = (9/5)C + 32 ; F = 91
91 = (9/5)C + 32
59 = (9/5)C Subtracted 32 from both sides
295 = 9C Multiplied both sides by 5
32.8 = C Divided 9 from both sides
33 = C Rounded to the nearest whole number
21) Perimeter (P) = 2Length (L) + 2width (w)
Given: P = 120, L = 5w
P = 2L + 2w
120 = 2(5w) + 2w
120 = 10w + 2w
120 = 12w
10 = w
L = 5w
= 5(10)
= 50
As part of a science experiment, a student recorded 10 measurements of the temperature of a liquid. One of the measurements was an outlier when compared with the other 9 measurements. Which of the following must be true about the 9 measurements, excluding the outlier, when compared with the 10 measurements? (Note: An outlier is any number that is greater than the upper quartile or less than the lower quartile by at least 1.5 times the interquartile range.) (A) The median of the 9 measurements is less than the median of the 10 measurements. (B) The median of the 9 measurements is greater than the median of the 10 measurements. (C) The maximum of the 9 measurements is less than the maximum of the 10 measurements. (D) The maximum of the 9 measurements is greater than the maximum of the 10 measurements. (E) The standard deviation of the 9 measurements is less than the standard deviation of the 10 measurements.
Answers
Among the given options, (C) The maximum of the 9 measurements is less than the maximum of the 10 measurements must be true about the 9 measurements, excluding the outlier, when compared with the 10 measurements.
An outlier is defined as a measurement that significantly deviates from the other measurements in a data set.
In this case, one of the measurements among the 10 is identified as an outlier.
When comparing the remaining 9 measurements with the entire set of 10 measurements, the maximum value of the 9 measurements cannot exceed the maximum value of the 10 measurements because the outlier, by definition, exceeds the upper quartile or lower quartile by at least 1.5 times the interquartile range.
It is important to note that the median of the 9 measurements can be either greater than or less than the median of the 10 measurements, depending on the specific values of the measurements.
The presence of the outlier does not necessarily determine the relationship between the medians of the two sets.
Similarly, the standard deviation of the 9 measurements may or may not be less than the standard deviation of the 10 measurements.
The inclusion or exclusion of the outlier can have an impact on the standard deviation calculation, but it is not guaranteed to be lower or higher in either case.
Therefore, among the given options, the only statement that must be true is (C) The maximum of the 9 measurements is less than the maximum of the 10 measurements.
Learn more about standard deviation here:
https://brainly.com/question/30014356
#SPJ11
Bike sprockets and chain.
Which of the following gear ratios will have the highest overall speed?
2.26
2.87
3.5
4.63
Answers
Answer:
4.63
Step-by-step explanation:
Answer:
The correct answer is 4.63
Step-by-step explanation:
Have a good day!
Which scales of data measurement are associated with quantitative data? interval and ratio ratio and nominal ordinal and interval nominal and ordinal
Answers
Interval and ratio scales of data measurement are associated with quantitative data.
Data measurement:- Data measurement is the way in which data can be subcategorized to analyze the data properly. Data can be classified into two types-
Quantitative data:- The data, which can be measured with numbers is called as quantitative data. Ex: duration, speed etc. This kind of data can be again subcategorized into two types-Discrete:- The data, which is of whole number, that can't be broken. Ex: a number of items.Continuous:- The data, which can be broken. Ex: height, weight etc. This type of data can be measured using interval and ratio measurement scales.Qualitative data:- The data, which is non-numerical value and categorical is called as qualitative data. Ex: yes, no responses or eye color etc. This type of data can be measured using nominal and ordinal measurement scales.Thus we can conclude that, Interval and ratio scales of data measurement are associated with quantitative data.
To know more about data measurement refer below link:
https://brainly.com/question/23894295
#SPJ4
What is the slope intercept form (y=mx+b) of the equation 5x-3y=15
Answers
Answer:
y= -5/3 + 5
Step-by-step explanation:
5x-3y=15 first move the 5x to the right side of the equation which becomes 3y= -5x +15 and then divide the whole equation by 3 because u want y to be on its own so then the answer is y= -5/3 + 5
1) Louis is dilating triangle ABC at right. He
multiplied each x-coordinate and y-coordinate of
triangle ABC by -2.
a. What are the new coordinates of the points?
Answers
To find the new coordinates of the points after Louis multiplied each x-coordinate and y-coordinate of triangle ABC by -2, we can use the following formulas:
New x-coordinate = -2 * old x-coordinate
New y-coordinate = -2 * old y-coordinate
Let's apply these formulas to each point in triangle ABC:
Point A: (-3, 4)
New x-coordinate of A = -2 * (-3) = 6
New y-coordinate of A = -2 * 4 = -8
New coordinates of A: (6, -8)
Point B: (1, 1)
New x-coordinate of B = -2 * 1 = -2
New y-coordinate of B = -2 * 1 = -2
New coordinates of B: (-2, -2)
Point C: (5, -2)
New x-coordinate of C = -2 * 5 = -10
New y-coordinate of C = -2 * (-2) = 4
New coordinates of C: (-10, 4)
Therefore, the new coordinates of the points after Louis multiplied each x-coordinate and y-coordinate of triangle ABC by -2 are:
A: (6, -8)
B: (-2, -2)
C: (-10, 4)
PLEASEEEEE HELPPPPPPP!!!! WILL GIVE BRAINLIEST Which of Euclid's postulates seems most unlike the others?
-A straight line segment can be drawn between any two points.
-Any straight line segment can be extended indefinitely.
-A circle can be drawn with any center and radius.
-All right angles are equal to one another.
-If two straight lines in a plane are met by another line, and if the sum of the interior angles on one side is less than two right angles, then the straight lines, if extended sufficiently, will meet on the side upon which the sum of the angles is less than two right angles.
Answers
Answer:If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles
Brainliest for correct answer

Answers
Answer:
s = 120
r = 33
t = 33
Step-by-step explanation:
You are solving for the variables r & t & s. Note that it is given that the two parallelograms are congruent with each other.
Make sure that they are facing the same way. Note that DC ≅ GH, AD ≅HE, FE ≅ AB
Solve:
DC ≅ GH; 70 = s - 50
Isolate the variable, note the equal sign, what you do to one side, you do to the other. Add 50 to both sides;
70 (+50) = s - 50 (+50)
s = 70 + 50
s = 120
Solve:
AD ≅ HE
2r = 66
Isolate the variable, divide 2 from both sides:
(2r)/2 = (66)/2
r = 66/2
r = 33
Solve:
FE ≅ AB
t + 50 = 83
Isolate the variable, subtract 50 from both sides:
t + 50 (-50) = 83 (-50)
t = 83 - 50
t = 33
what is the probability of an offspring from the model 2 population getting a dominant allele? use a decimal.
Answers
The frequency of the dominant allele in the population is 0.6.
Let's begin with the fundamental Hardy-Weinberg equations.
p + q = 1 and p² + 2pq + q² = 1
whereby "q" is the recessive allele and "p" is the dominant allele.
Recessed traits are present in 16% of people, or 0.16 percent. This indicates the percentage of the population that possesses the recessive trait,
q², is 0.16.
It is possible to calculate q using the value for q². What comes next is that q = 0.4.
This information allows for the calculation of "p".
1 − q = p , which results in "p" being 0.6.
This 0.6 is the frequency at which the dominant allele is prevalent in the population.
To learn more about Hardy-Weinberg equations link is here
brainly.com/question/29776155
#SPJ4
The complete question is:
In a population that is in Hardy-Weinberg equilibrium, 16% of the individuals show the recessive trait. What is the frequency of the dominant allele in the population?
what is the mean, median, mode, and range of
1) 2,3, 1, 1, 3
2) 10, 8, 9, 8, 5
3) 13, 8, 11, 7, 5, 10
Answers
two numbers have ratio 12:5. Their difference is 98. Find the larger
number.
Answers
Work out the size of the interior angle of a regular 18-sided polygon.
Answers
Answer:
160°
Step-by-step explanation:
The formula below gives the measure of an interior angle of a regular polygon of n sides.
[(n - 2)180]/n
[(18 - 2)180]/18
16(10)
160
Answer: 160°
Jimmys garden has a length of 2b
+ 4 and a width of 7b + 2. What is
the perimeter of the garden?
Answers
Answer: 18b + 2
Step-by-step explanation:
Length: 2b + 4
Width: 7b + 2
I assumed the garden is a rectangle shape since the length and width are different.
Perimeter = 2( L + w)
Then we just plug the values in.
2 (2b + 4 + 7b + 2)
2 (9b + 6) = 18b + 12
So, the equation for the perimeter of Jimmy's garden will be 18b + 2.