Answers
Answer:
Step-by-step explanation:
1) 1 7/9 = 9*1+7/9 = 16/9
2) 6 3/4 = 6*4+3/4 = 27/4
3) 11 1/5 = 11*5+1/5 = 56/5
4) 5 2/6 = 5*6+2/6 = 32/6
5) 10 3/7 = 10*7+3/7 = 73/7
Hope you understood!!
Related Questions
The Tonka Toy Company has a profit of P(x)=30x-300 dollars when d RC Trucks are sold a month. 1. Find an inverse function for this model. Show work. 2. Use the inverse to find the amount of Trucks needed to produce a profit of $20,000. Show work.
Answers
1. The inverse function is found isolating x, as follows:
\(\begin{gathered} P(x)=30x-300 \\ P(x)+300=30x \\ \frac{P(x)+300}{30}=x \\ \frac{P(x)}{30}+\frac{300}{30}=x \\ \frac{1}{30}P(x)+10=x \end{gathered}\)Changing the name of the variables, the inverse function is:
\(y=\frac{1}{30}x+10\)where y represents the amount of trucks and x the profit.
2. Replacing with x = 20,000 into the inverse function, we get:
\(\begin{gathered} y=\frac{1}{30}\cdot20000+10 \\ y=666.67+10 \\ y=676.67 \end{gathered}\)The amount of Trucks needed to produce a profit of $20,000 is 677
Luke is also making pizzas. He started with 4 1/2 cups of pepperoni. He has used 2/3 of his pepperoni. How many cups of pepperoni has he used so far?
2 cups
4 3/5 cups
3 cups
4 1/3 cups
Explain your reasoning.
Answers
Answer:
3 cups
Step-by-step explanation:
Luke has 1 1/2 cups of pepperoni left
4 5/6 - 4 1/3 in simplest form
Answers
\(\huge\text{Hey there!}\)
\(\mathsf{4\dfrac{5}{6}-4\dfrac{1}{3}\ =}\)
\(\mathsf{4\dfrac{5}{6}=\bf \dfrac{29}{6}}\)
\(\mathsf{4\dfrac{1}{3}=\bf \dfrac{13}{3}}\)
\(\mathsf{\dfrac{29}{6}-\dfrac{13}{3}}\)
\(\mathsf{\dfrac{(29\times3)-(13\times6)}{6\times3}}\)
\(\mathsf{29\times3 = \bf 87}\leftarrow \large\textsf{\underline{NUMERATOR}}\)
\(\mathsf{13\times6= \bf 78}\leftarrow\large\textsf{\underline{NUMERATOR}}\)
\(\mathsf{\dfrac{\bf 87-78}{6\times3}}\)
\(\mathsf{87-78=\bf 9}\leftarrow\large\textsf{\underline{NUMERATOR}}\)
\(\mathsf{\dfrac{\bf 9}{6\times3}}\)
\(\mathsf{6\times3 = \bf 18}\leftarrow\large\textsf{\underline{DENOMINATOR}}\)
\(\mathsf{\dfrac{9}{\bf 18}}\)
\(\mathsf{\dfrac{9\div9}{18\div9}}\)
\(\mathsf{9\div9=\bf 1}\leftarrow \large\textsf{NUMERATOR}\)
\(\mathsf{\dfrac{\bf 1}{18\div9}}\)
\(\mathsf{18\div9= \bf 2}\leftarrow\large\textsf{DENOMINATOR}\)
\(\mathsf{ = \dfrac{1}{\bf 2}}\)
\(\boxed{\boxed{\large\text{Answer: }\mathsf{\bf \dfrac{1}{2}}}}\huge\checkmark\)
\(\text{Good luck on your assignment and enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
What does 37.26 x 1,000 = ?
Answers
Answer:
37,260
Step-by-step explanation:
84-24
24x84
84x24
plz help me

Answers
Answer:
-493565100
Step-by-step explanation:
1
Combine exponents
8
4
−
2
4
2
4
YASSSSSSSSSSS
HELPPPPPPP A SISTA OUT
LoL

Answers
Answer:
8 are from South Africa
Step-by-step explanation:
1/4 + 5/8
2/8 + 5/8
1-7/8= 1/8
1/8 of 64 is equal to 8
Compare the investment below to an investment of the same principal at the same rate compounded annually.
principal: $5,000, annual interest: 9%, interest periods: 4, number of years: 18
After 18 years, the investment compounded periodically will be worth $? more than the investment compounded annually.
(Round to two decimal places as needed.)
Answers
After 18 years, the investment compounded periodically (quarterly) will be worth $1,230.23 more than the investment compounded annually.
What is compounded interest?Compounded interest refers to the interest system that charges interest on both principal and accumulated interest.
The period of compounding in a year determines the worth of the future value.
The future value can be ascertained using an online finance calculator as follows:
Interest periods: = 4 times yearly (Quarterly)
Principal = $5,000
Annual interest rate = 9%
Number of years: 18
N (# of periods) = 72 quarters (18 years x 4)
I/Y (Interest per year) = 9%
PV (Present Value) = $5,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $24,815.83
Total Interest = $19,815.83
Interest periods: = Annually
N (# of periods) = 18 years
I/Y (Interest per year) = 9%
PV (Present Value) = $5,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $23,585.60
Total Interest = $18,585.60
Difference in Future Values $1,230.23 ($24,815.83 - $23,585.60)
Thus, an investment compounded periodically earns more than an investment compounded annually.
Learn more about compounded interest at https://brainly.com/question/28020457.
#SPJ1
a triangle window has area 24 square feet and height six feet. what is its base? define variable, and set up and solve an equation to answer this.
Answers
Answer:
6*y/2=24
24*2=48
48/6=8
y=8
Step-by-step explanation:
The equation will be 24 = \(\frac{1}{2}\) × b × 6 value of base will be b = 8 ft .
A triangle has area 24 square ft. and height 6 ft.
What will be its base. Find an equation also.
What is the formula of area of triangle ?
Area of triangle is ; Area = \(\frac{1}{2}\) × b × h
∵ The equation of area of triangle will be ;
Area = A = \(\frac{1}{2}\) × b × h ----- - --- --- --- Equation 1
A = 24 = \(\frac{1}{2}\) × b × 6
⇒ b = \(\frac{24 * 2}{6}\) = \(\frac{48}{6}\) = 8
⇒ b = 8 ft.
Thus , the equation will be 24 = \(\frac{1}{2}\) × b × 6 value of base will be b = 8 ft .
To learn more about area of triangle click here ;
https://brainly.com/question/23945265
#SPJ2
helpppp...........................

Answers
Answer:
see explanation
Step-by-step explanation:
the sum of the interior angles of a polygon is
sum = 180° (n - 2) ← n is the number of sides
a hexagon has 6 sides , then
sum = 180° × (6 - 2) = 180° × 4 = 720°
12
the polygon has 5 sides , so
sum = 180° × (5 - 2) = 180° × 3 = 540°
sum the interior angles and equate to 540
y + 90 + 120 + 90 + 110 = 540
y + 410 = 540 ( subtract 410 from both sides )
y = 130
13
the polygon has 7 sides , so
sum = 180° × (7 - 2) = 180° × 5 = 900°
sum the interior angles and equate to 900
p + 90 + 141 + 130 + 136 + 123 + 140 = 900
p + 760 = 900 ( subtract 760 from both sides )
p = 140
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
in triangle JKL, angle JKL is a right angle, line KM is an altitude, JL=20, ML=4. Find KM
Answers
9514 1404 393
Answer:
KM = 8
Step-by-step explanation:
The ratio of long side to short side is the same for all of the triangles in this geometry:
KM/ML = JM/KM
KM² = ML·JM = 4(20-4) = 64
KM = √64 = 8
The length of KM is 8 units.
You roll a six-sided die. Find the probability of each of the following scenarios
(a) Rolling a 6 or a number greater than 3
(b) Rolling a number less than 5 or an even number
(c) Rolling a 4 or an odd number
---
(a) P(6 or number > 3) = 0.500 (Round to three decimal places as needed)
(b) P(1 or 2 or 3 or 4 or 6) =
(Round to three decimal places as needed.)
Answers
Answer:
a) \(1/2\)
b) \(5/6\)
c) \(2/3\)
Step-by-step explanation:
a)
Rolling a number greater than 3 means you can roll a 4, 5, or 6, which contains rolling a 6. So, the probability is \((1+1+1)/6=3/6=\boxed{1/2}\)
b)
Rolling a number less than 5 means you can roll a 1, 2, 3, or 4, but because you could also roll an even number, so you could also roll a 6.
So, the probability is \((1+1+1+1+1)/6=\boxed{5/6}\)
c)
Rolling a 4 or an odd number means you can roll a 1, 3, 5, or 4. So, the probability is \((1+1+1+1)/6=4/6=\boxed{2/3}\)
Hence, Solve the equation
X Х
1- x
4x=
Answers
I need help please!!!!!!
Tom completed the problem below incorrectly.
Explain what mistake he made. ALSO include the
correct answer.
23 - 8.2 + 3
23 - 16 + 3
23 - 19
4
Answers
Answer:
12
Step-by-step explanation:
He went wrong when he did 16 + 3 first when he should have done 23 minus 16 which is 9. Then 9 plus 3 equals 12.
find the value of x.

Answers
Answer:
x=8
Step-by-step explanation:
Set 40 + y = 90
y=50
y = 6x + 2
6x + 2 = 50
6x = 48
48/6 = x
x=8
Answer:
8
Step-by-step explanation:
(6x + 2) + 40 = 90 because the entire angle is a right angle, therefore the whole angle is 90
subtract 40 from each side: 6x + 2 = 50
now subtract 2 from each side: 6x = 48
now divide 6 from each side: x = 8
what is an example of "The restriction of a function f"?

Answers
The restriction of a function f is when the domain of f is limited to a subset of its original domain.
What is an example of "The restriction of a function f"?The restriction of a function f can be demonstrated by considering a function f: R -> R, where R represents the set of real numbers.
Let u say f(x) = x^2. Now, if we restrict the domain of f to the interval [0, 5], the new function becomes f restricted: [0, 5] -> R and its expression would be f restricted(x) = x^2 for x in the interval [0, 5].
This means that the function f restricted only takes inputs from the interval [0, 5] and behaves the same way as the original function within that interval.
Read more about function
brainly.com/question/11624077
#SPJ1
PLEASE HELP! The height of a bottle rocket, in meters, is given by \(h(t) = -3t^{2} +36t+300, where t is measured in seconds. Compute the average velocity of the bottle rocket over the time interval t = 3 to t = 6.
Answers
Answer:
63 m/s
Step-by-step explanation:
h(3) = 3(3)² + 36(3) + 300 = 435
h(6) = 3(6)² + 36(6) + 300 = 624
v = Δh/Δt = (624m - 435m) / (6s - 3s) = 63 m/s
can someone please help

Answers
Answer:
The measure of CD is 46
Step-by-step explanation:
From the midpoint theorem, we have,
FG = (1/2)CD
so,
\(13+5x=(1/2)(-3x+52)\\So,\\2(13+5x)=-3x+52\\26+10x=-3x+52\\13x=52-26\\13x=26\\x=26/13\\x=2\)
Now,
\(CD = -3x+52\\since \ x=2\\we \ get\\CD=-3(2) +52\\CD=-6+52\\CD=46\)
The area of a parallelogram can be calculated with A=bh. Knowing this, please calculate the area of the followings:
2 points
Captionless Image
30 units squared
12 units squared
6 units squared
24 units squared

Answers
Answer:
24 units ²Step-by-step explanation:
to understand thisyou need to know about:coordinate geometryPEMDAStips and formulas:area:b×hdistance from A and C point is 4 unitsdistance from C and D point is 6 unitslet's solve:use the formula:4×6 units²simplify multiplication:24 units²Solving a word problem on proportions using a unit rate
Dante drove 871 miles in 13 hours.
At the same rate, how long would it take him to drive 603 miles?
Answers
The unit rate of miles per hour is:
871 miles ÷ 13 hours = 67 miles per hour
This means that Dante drove at a rate of 67 miles per hour.
To find out how long it would take him to drive 603 miles at the same rate, we can set up a proportion:
871 miles ÷ 13 hours = 603 miles ÷ x hours
We can cross-multiply to solve for x:
871x = 13 * 603
871x = 7,839
x = 9
Therefore, it would take Dante 9 hours to drive 603 miles at the same rate of 67 miles per hour.
What is the slope of a line perpendicular to the line whose equation is 3x-3y=54. Fully simplify your answer.
Answers
Make equation into y = mx + b
Add 3y to both sides
3y + 54 = 3x
Subtract 54
3y = 3x - 54
Divide by 3
y = x - 18
The slope is 1
Make it negative and reciprocal
= -1/1 = -1
Solution: the slope will be -1
Help me solve this question

Answers
After the rotation of the figure TEAM at 180° from origin, the new coordinates of T'E'A'M' are:
T' = (-3, 2)E' = (-2, -4)A' = (2, -3)M' = (-6, -7)What is rotation?The concept of rotation in mathematics has its roots in geometry. Any rotation is a movement of a certain area while maintaining at least one point. It may be used to describe, for instance, how a rigid body moves around a fixed point. A clockwise rotation has a negative magnitude, whereas a counterclockwise turn has a positive magnitude (much like the sign of an angle). In contrast to translations, which have no fixed points, and (hyperplane) reflections, which each have a whole (n 1)-dimensional flat of fixed points in an n-dimensional space, a rotation has fixed points.So, rotate TEAM at 180°:
Rotate on origin as follows:(Refer to the graph attached below):After the rotation, the coordinates of T'E'A'M' are:
T' = (-3, 2)E' = (-2, -4)A' = (2, -3)M' = (-6, -7)Therefore, after the rotation of the figure TEAM at 180° from the origin, the new coordinates of T'E'A'M' are:
T' = (-3, 2)E' = (-2, -4)A' = (2, -3)M' = (-6, -7)Know more about rotation here:
https://brainly.com/question/26249005
#SPJ13

Select the number that round to 387.4 when rounded to the nearest tenth.
A. 387.461
B. 387.344
C. 387.309
D. 387.352
E. 387.779
Answers
Answer:
D
Step-by-step explanation:
When rounding, the number 5 is rounded up. So the number 387.352 will be rounded up 387.4. Other options are not suitable. Correct answer is "D"
If you think my answer is the best, please mark it as the Brainliest.
Thank you! :))
7
The venue for an outdoor summer concert was divided into 35 sections. The event planner randomly chose 8 sections and counted
the number of ice chests in the section, as shown below.
48, 51, 26, 73, 51, 48, 26,51
Assuming that the sample was representative of the entire venue, what was the mean number of ice chests in a section?
Answers
The mean number of ice chests in a section is 46.75.
How do we find the mean number of ice chests?The mean is the average or the most common value in a collection of numbers. In statistics, it is a measure of central tendency along median and mode..
To find the mean number of ice chests in a section, we need to calculate the sum of the ice chests and then divide total number of sections sampled.
Sum of ice chests = 48 + 51 + 26 + 73 + 51 + 48 + 26 + 51
Sum of ice chests = 374
Mean number of ice chests will be:
= (Sum of ice chests) / (Total number of sections sampled)
= 374 / 8
= 46.75
Read more about Mean
brainly.com/question/1136789
#SPJ1
What is m∠PTR? a. 12 b. 40 c. 50 d. 140 HELP!!!

Answers
Answer:
m<PTR = 140°
Step-by-step explanation:
First, find the value of x. To find the value of x, derive an equation which you'd use in solving for x.
m<PTQ = (x + 28)°
m<RTS = (2x + 16)°
m<PTQ = m<RTS (vertical opposite angles are congruent)
Therefore:
x + 28 = 2x + 16
Solve for x. Combine like terms
28 - 16 = 2x - x
12 = x
x = 12
Find m<PTQ
m<PTQ = (x + 28)
plug in the value of x
m<PTQ = 12 + 28 = 40°
m<PTR + m<PTQ = 180° (supplementary angles)
m<PTR + 40° = 180° (substitution)
m<PTR = 180 - 40 (subtracting 40 from each side)
m<PTR = 140°
which table shows a relationship between the values of x and y that represents a linear function?

Answers
5. Circle the correct relationship below and explain your choice. I. All trapezoids are parallelograms. II. All parallelograms are trapezoids. Explanation:
Answers
Parallelograms and trapezoids are both two-dimensional shapes with four sides. While they share similarities, there are some key differences between the two that help to distinguish them from each other. In this essay, we will discuss the key differences between parallelograms and trapezoids and explore how these differences can help us to identify each shape.
A parallelogram is a two-dimensional shape with four sides and two sets of parallel lines. It is a quadrilateral with opposite sides parallel to each other and opposite angles equal. A parallelogram can also have opposite sides of equal length, which is known as a rhombus. Examples of shapes that are parallelograms include squares, rectangles, and rhombuses.
A trapezoid is also a two-dimensional shape with four sides. However, unlike a parallelogram, a trapezoid only has one set of parallel lines. The two non-parallel sides of a trapezoid are called the legs, while the two parallel sides are called the bases.
Learn more about parallelograms:
https://brainly.com/question/20695223
#SPJ4
i need answer, pls help
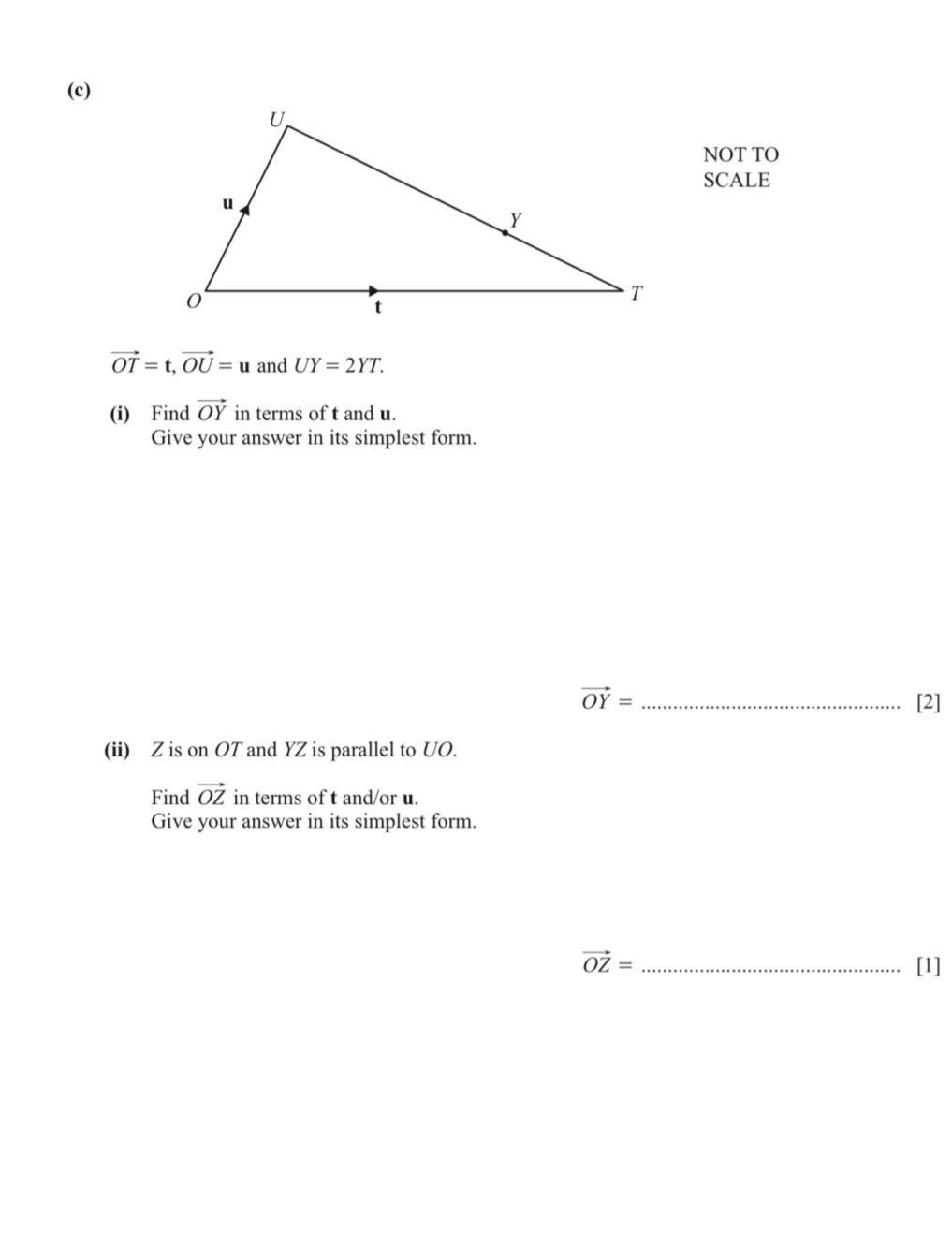
Answers
Case 1 - By vector subtraction, the equation of the vector is \(\overrightarrow {OY} = 2\cdot t - u\).
Case 2 - By proportion formula, the equation of the vector is \(\overrightarrow{OZ} = \frac{2}{3}\cdot t\).
How to derive the equation of a vector
In this problem we find two case of vectors that must be determined. The first case consists in a case of a vector subtraction, based on the following conditions:
\(\overrightarrow{OU} = t\), \(\overrightarrow{OU} = u\), \(\overrightarrow{UY} = 2\cdot \overrightarrow{YT}\)
\(\overrightarrow{OY} = \overrightarrow{OT} + \overrightarrow{YT}\)
\(\overrightarrow {OY} = \overrightarrow{OU} + \overrightarrow{UY}\)
First, eliminate UY:
\(\overrightarrow{OY} = \overrightarrow{OU} + 2\cdot \overrightarrow{YT}\)
\(\overrightarrow{OY} = u + 2\cdot \overrightarrow{YT}\)
\(\overrightarrow{OY} = \overrightarrow{OT} + \overrightarrow{YT}\)
\(\overrightarrow {OY} = t + \overrightarrow {YT}\)
Second, eliminate OY and clear YT:
\(u + 2 \cdot \overrightarrow{YT} = t + \overrightarrow{YT}\)
\(\overrightarrow{YT} = t - u\)
Third, determine the vector OY:
\(\overrightarrow {OY} = t + \overrightarrow {YT}\)
\(\overrightarrow {OY} = 2\cdot t - u\)
The second case required the determination of a vector parallel to vector OU (vector ZY). Two vectors are parallel when both have the same direction.
First, determine the expression for vector UY:
\(\overrightarrow{UY} = 2\cdot (t - u)\)
Second, determine the expression for vector UT:
\(\overrightarrow {UT} = 2 \cdot (t - u) + (t - u)\)
\(\overrightarrow {UT} = 3\cdot (t - u)\)
Third, derive the expression of vector ZY by proportion formula:
ZY / OU = YT / UT
ZY = OU · (YT / UT)
ZY = ||u|| · [||t - u|| / (3 · ||t - u||)]
ZY = ||u|| / 3
\(\overrightarrow {ZY} = \frac{1}{3}\cdot u\)
Fourth, derive the expression of vector OZ by proportion formula:
ZT / OT = ZY / OU
ZT = OT · (ZY / OU)
ZT = ||t|| · (||(1 / 3) · u|| / ||u||)
ZT = (1 / 3) · ||t||
OZ = OT - ZT
OZ = ||t|| - (1 / 3) · ||t||
OZ = (2 / 3) · ||t||
\(\overrightarrow{OZ} = \frac{2}{3}\cdot t\)
To learn more on vectors: https://brainly.com/question/4579006
#SPJ1
A florist currently makes a profit of $20 on each of her celebration bouquets and sells an average of 30 bouquets every week. She noticed that when she reduces the price such that she earns $1 less in profit from each bouquet, she then sells three more bouquets per week. The relationship between her weekly profit, P(x), after x one-dollar decreases is shown in the graph below.
A graph for p of x is a downward open parabola with its vertex at (5, 725) and passes through the points (negative 10, 0), and (20, 0).
Use the graph to complete each statement about this situation.
The maximum profit the florist will earn from selling celebration bouquets is $.
The florist will break-even after one-dollar decreases.
The interval of the number of one-dollar decreases for which the florist makes a profit from celebration bouquets is ( , ).
Answers
Answer:
The maximum profit the florist will earn from selling celebration bouquets is $725.
The florist will break-even after one-dollar decreases when her profit is zero. From the graph, this occurs at x = 10. So the florist will break-even after 10 one-dollar decreases.
The interval of the number of one-dollar decreases for which the florist makes a profit from celebration bouquets is (0, 10). This is because the profit is positive for values of x between 0 and 10, and becomes negative after 10.
Step-by-step explanation:
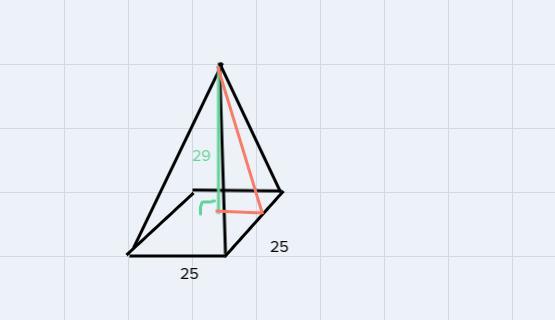
what is the lateral area of the rectangular pyramid whose net is shown
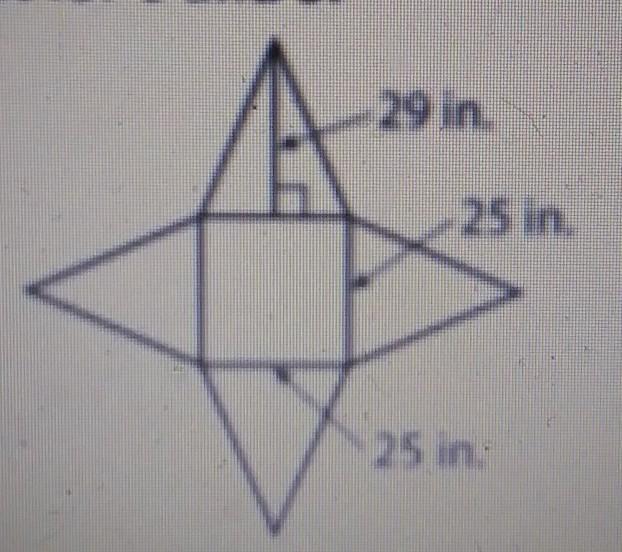
Answers
Given the information on the picture, we have the following rectangular pyramid:
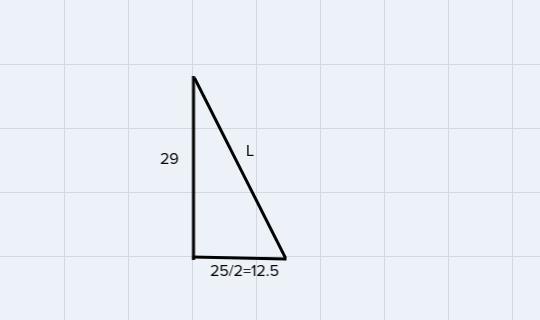
Notice that we get the following right triangle:
then we can use the pythagorean theorem to find the missing length:
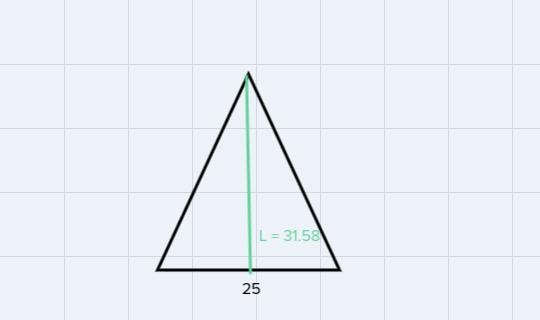
\(\begin{gathered} L^2=(29)^2+(12.5)^2 \\ \Rightarrow L^2=841+156.25=997.25 \\ \Rightarrow L=\sqrt[]{997.25}=31.58 \\ L=31.58in \end{gathered}\)Now we have the base and the height of a lateral side:
Then, using the formula for the area of a triangle, we get the following:
\(\begin{gathered} A=\frac{b\cdot L}{2}=\frac{25\cdot31.58}{2}=\frac{789.5}{2}=394.75 \\ A=394.75in^2 \end{gathered}\)therefore, the lateral area of the rectangular pyramid is 394.75 in^2