Answers
Explanation: slope = rise/run = -500/1 = -500
Hope this helps! :)
Related Questions
Evaluate 7m + 2n - 8p/n for m = –4, n = 2, and p = 1.5.
Answers
Answer:
-30
Step-by-step explanation:
7m + 2n - 8p/n
Let m = –4, n = 2, and p = 1.5
7(-4) + 2 ( 2) -8*(1.5)/2
-28 + 4 - 4*1.5
-28+ 4 - 6
-30
Answer:
-30
Step-by-step explanation:
Hey there!
Well given,
m = -4
n = 2
p = 1.5
We need to plug those number into,
7m + 2n - 8p/n
7(-4) + 2(2) - 8(1.5)/(2)
-28 + 4 - 12/2
-28 + 4 - 6
-24 - 6
-30
Hope this helps :)
Explain the difference between (-5)2 and
-52.
Answers
Answer:
the parentheses say that you have to multiply -5 and 2
where as -52 is just a number.
Answer:
(-5)2 = -10 (you multiply because of the parenthesis)
Step-by-step explanation:
(-5)2 = -5 × 2 = -10
-52 is just a negative intenger.
find a formula for an for the arithmetic sequence:a1=-1,a5=7
Answers
Answer:
\(a_{n}\) = 2n - 3
Step-by-step explanation:
the nth term of an arithmetic sequence is
\(a_{n}\) = a₁ + d(n - 1)
where a₁ is the first term and d the common difference
given a₁ = - 1 and a₅ = 7 , then
a₁ + 4d = 7 , that is
- 1 + 4d = 7 ( add 1 to both sides )
4d = 8 ( divide both sides by 4 )
d = 2
then
\(a_{n}\) = - 1 + 2(n - 1) = - 1 + 2n - 2 = 2n - 3
\(a_{n}\) = 2n - 3
what is the value of the expression 2[4(2^3+5)]-4^2
Answers
2 [4( 2³ + 5)] - 4²
2 [ 4 (8 + 5)] - 16
2 [ 4 ( 13)] - 16
2 [ 52 ] - 16
104 - 16
88
Good Studies!
![what is the value of the expression 2[4(2^3+5)]-4^2](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/I4WlAzP2jG7nlRKa9gkSsi1dI5thqcwI.jpeg)
G (x ), represents transformations on the parent function of y = (½) x Write the equation for g (x ).
Answers
Complete Question:
g(x), represents transformations on the parent function of \(y = (\frac{1}{2})^x\).
Write the equation for g (x ) with the following transformations:
Reflect over y-axis, and shift right 7
Answer:
\(g(x) = (\frac{1}{2})^{-x-7}\)
Step-by-step explanation:
Given
\(y = (\frac{1}{2})^x\)
Represent the function as:
\(f(x) = (\frac{1}{2})^x\)
Taking the transformations, one after the other:
Reflect over the y-axis.
This is represented by the rule: (x,y) ==> (-x,y)
So, we have:
\(f'(x) = (\frac{1}{2})^{-x}\)
Shift right 7 units
This is represented by (x,y) = (x - b, y)
Where b represents the number of units
So, we have:
\(f'(x-7) = (\frac{1}{2})^{-x-7}\)
Hence:
\(g(x) = (\frac{1}{2})^{-x-7}\)
Trisha uses 3 cups of sugar for every 4 cups of flour to make a batch of cookies. Which equation could be used to solve x, the number of cups of flour needed for 9 cups of sugar.
Answers
Answer: The number of cups of flour needed for 9 cups of sugar = 12.
Step-by-step explanation:
Equation of direct proportion between two quantities x and y :
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Let x= the number of cups of flour needed for 9 cups of sugar.
Put \(x_1=4,\ y_1=3,\ y_2=9, x_2=x\)
\(\dfrac{4}{3}=\dfrac{x}{9}\\\\\Rightarrow\ x=\dfrac{9\times4}{3}\\\\\Rightarrow\ x=12\)
Hence, the number of cups of flour needed for 9 cups of sugar = 12.
Hugh made a recipe that yields 8 and 1 over 2 cups. If each serving is 1 over 4 cup, which expression will help Hugh determine the number of servings his recipe will yield? 8 and 1 over 2 ⋅ 1 over 4 8 and 1 over 2 + 1 over 4 8 and 1 over 2 − 1 over 4 8 and 1 over 2 ÷ 1 over 4
Answers
A recipe yields = 8(1/2) cups.
And,
Each serving = (1/4) cups.
Therefore,
The number of servings his recipe will yield = (Total recipe yields) ÷ (Each serving) = 8(1/2) ÷ (1/4) = 8 and 1 over 2 ÷ 1 over 4 (Option D).
identify the congruent criteria (mcqs)
pls answer all of them

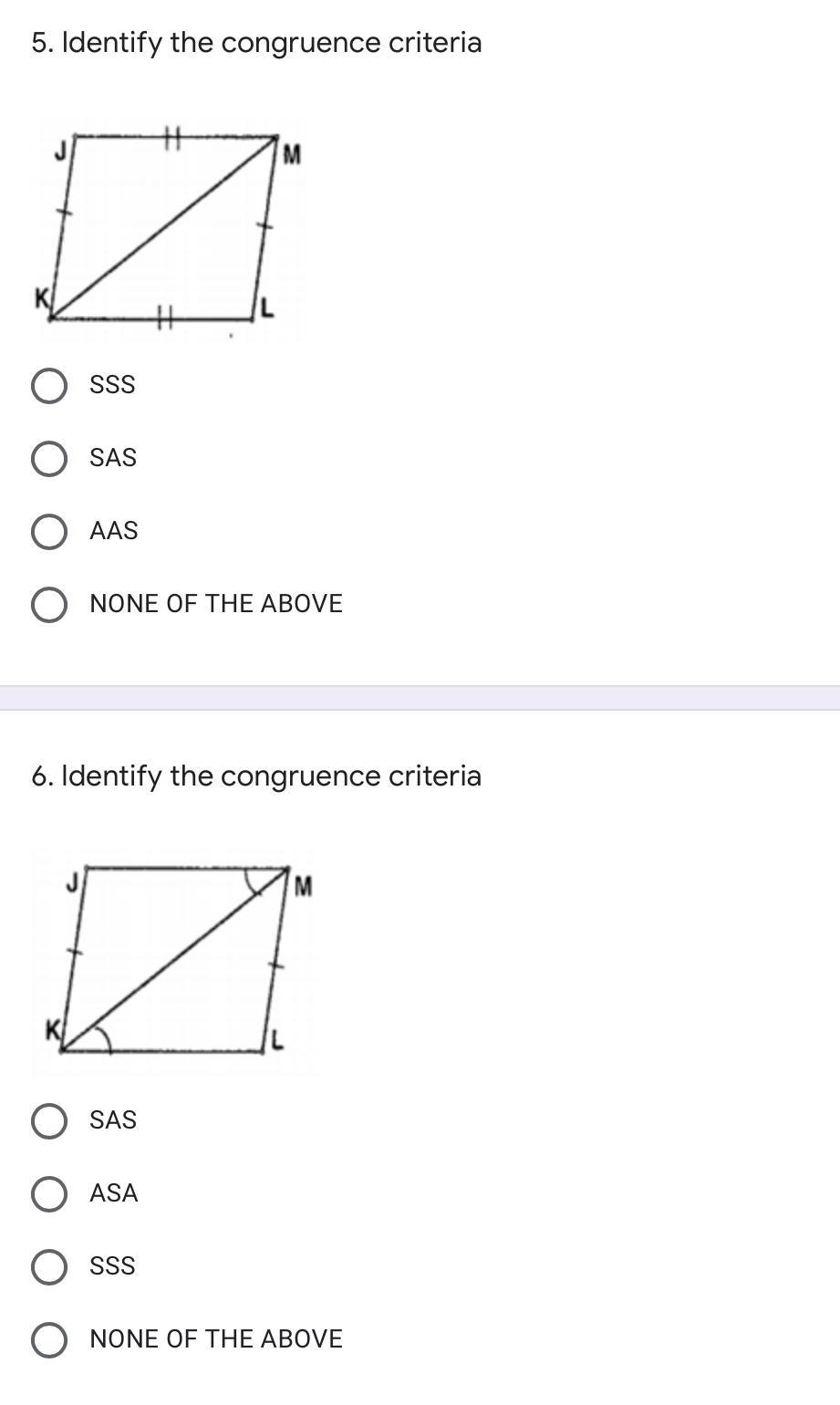

Answers
6. ASA
7. SAS
8. ASA
9. ASA
The notation "f(x)" (f of x) is another way of representing y-values in a function question 1 options: true false
Answers
The given statement " the notation "f(x)" is another way of representing y-values in a function" is true because f (x) and y are the same things.
The notation f(x), read as "f of x", indicates a function named f. It reflects that 'y is a function of x'. The letter 'x' refers to the input value or independent variable. While the letter 'y' is replaced by f(x) and it refers to the output value or dependent variable.
The notation 'f (x)' is exactly the same as that of 'y'. Even on graphs, y-axis can be labelled with 'f (x)'.
You can learn more about f (x) at
https://brainly.com/question/27887777
#SPJ4
A quadrilateral has a total area of 36. 18 square inches. One of the sides measures 6. 7 inches. How long is the other side? inches
(do not include any words in the answer blank)
Answers
The length of the other side of the quadrilateral is 10.67 inches.
The other side of the quadrilateral measures 10.67 inches. This can be found by using the formula for the area of a quadrilateral, which is (1/2) x diagonal x height. We know the total area and one side length, so we can solve for the height. The height is 10.67 inches, which is the length of the other side.
To find the length of the other side of the quadrilateral, we need to use the formula for the area of a quadrilateral, which is (1/2) x diagonal x height.
We know the total area of the quadrilateral is 36.18 square inches, and we can assume that the side given (6.7 inches) is one of the diagonals. We can solve for the height, which represents the length of the other side.
Using algebra, we can rearrange the formula to solve for the height:
Area = (1/2) x diagonal x height
36.18 = (1/2) x 6.7 x height
Multiplying both sides by 2:
72.36 = 6.7 x height
Dividing both sides by 6.7:
height = 10.67 inches
To know more about quadrilateral click on below link:
https://brainly.com/question/3642328#
#SPJ11
Under what circumstances is a score that is located 5 points above the mean a central value, relatively close to the mean?
a. When the population standard deviation is much less than 5
b. When the population mean is much less than 5
c. When the population mean is much greater than 5
d. When the population standard deviation is much greater than 5
Answers
The circumstance that the score is located 5 points above the mean a central value, relatively close to the mean is when the population standard deviation is much greater than 5.
What is the standard deviation?Standard Deviation is a measure which shows how much variation (such as spread, dispersion, spread,) from the mean exists. The standard deviation indicates a “typical” deviation from the mean. It is a popular measure of variability because it returns to the original units of measure of the data set.
Here, we have
The circumstance is a score that is 5 points above the mean considered a central value.We have to find under what circumstances is a score that is 5 points above the mean considered a central value--meaning it is relatively close to the mean.
We concluded from the above statement that when the population standard deviation is much greater than 5.
Hence, when the population standard deviation is much greater than 5 then, the score that is 5 points above the mean is considered a central value.
Therefore, the correct option is D.
To know more on standard deviation, visit:
https://brainly.com/question/31298828
The price paid
for a $83.50
chair with an 8%
sales tax
What is the sale tax
Answers
Answer:
$6.68
Step-by-step explanation:
83.50(0.08) = 6.68
An independent set in a graph is a set of vertices S⊆V that contains no edge (so no pair of neighboring vertices is included). The max independent set problem is to find an independent set of maximum size in a graph G. (a) Write the max independent set problem as an integer linear program. (b) Write an LP relaxation for the max independent set problem. (c) Construct an example (a family of graphs) to show that the ratio LP-OPT / OPT can be at least cn where c>0 is some absolute constant and n is the number of vertices of the graph. (d) What is the (exact) relation between the size of a max independent set and the size of min vertex cover of a graph? (e) Using this relation, what does the 2-approximation algorithm for vertex cover imply for an approximation algorithm for max independent set?
Answers
The independent set in a graph is a set of vertices that contain no edges. So, no neighboring vertices are included. The max independent set problem is to get an independent set of maximum size in graph G.
The solution for this question is discussed below:
a) The integer linear program for the max independent set problem is as follows:
maximize ∑x_i Subject to: x_i+x_j ≤ 1 {i,j} ∈ E;x_i ∈ {0, 1} ∀i. The variable x_i can represent whether the ith vertex is in the independent set. It can take on two values, either 0 or 1.
b) The LP relaxation for the max independent set problem is as follows:
Maximize ∑x_iSubject to:
xi+xj ≤ 1 ∀ {i, j} ∈ E;xi ≥ 0 ∀i. The variable xi can take on fractional values in the LP relaxation.
c) The family of graphs is as follows:
Consider a family of graphs G = (V, E) defined as follows. The vertex set V has n = 2^k vertices, where k is a positive integer. The set of edges E is defined as {uv:u, v ∈ {0, 1}^k and u≠v and u, v differ in precisely one coordinate}. It can be shown that the size of the max independent set is n/2. Using LP, the value can be determined. LP provides a value of approximately n/4. Therefore, the ratio LP-OPT/OPT is at least c/4. Therefore, the ratio is in for a constant c>0.
d) The size of a max-independent set is equivalent to the number of vertices minus the minimum vertex cover size.
e) The 2-approximation algorithm for vertex cover implies a 2-approximation algorithm for the max independent set.
To know more about the independent set, visit:
brainly.com/question/31418821
#SPJ11
Select all the expressions that represent the area of the large, outer rectangle. * 3 points Captionless Image 5(2 + 4) 5 x 2 + 4 5 x 2 + 5 x 4 5 x 2 x 4 5 x 6
Answers
Step-by-step explanation:
121630....................................
Answer:
there isn't any pictur
Step-by-step explanation:
(4.2x10^6)(1.1x10^7)
Answers
Answer:4.62x10^13
Step-by-step explanation:
Help me please no links no

Answers
Answer:
x/4
Step-by-step explanation:
x + 4/4 = y + 3/3
do cross multiplication
4(y +3)=3(x +4)
4y +12=3x +12
4y=3x + 12 -12
4y=3x
y/3 = x/4
a pizza restaurant is located in a town with a population density of 1200 people per square mile. what delivery radius will allow the pizza restaurant to deliver to approximately 25,000 people?]
Answers
The delivery radius for a pizza restaurant in a town with a population density of 1200 people per square mile that wants to deliver to approximately 25,000 people is 2.6 miles.
To calculate the delivery radius, we can use the following formula:
Delivery radius = square root(population / density)
Use code with caution. Learn more
In this case, the population is 25,000 and the density is 1200 people per square mile. So, the delivery radius is:
Delivery radius = square root(25,000 / 1200) = 2.6 miles
Use code with caution. Learn more
This means that the pizza restaurant can deliver to approximately 25,000 people within a 2.6 mile radius of its location.
Here is another way to think about it. If we imagine a circle with a radius of 2.6 miles, then the area of that circle will be approximately 25,000 square miles. This means that the pizza restaurant can deliver to approximately 25,000 people within that circle.
It is important to note that this is just an estimate. The actual delivery radius may be slightly different depending on the terrain, traffic conditions, and other factors.
Learn more about square here: brainly.com/question/14198272
#SPJ11
let f(x) = 3x-2x^2 for 0
Answers
The solution is of the function 3f(x) +2g(x) is:
=> -5x-2
Now, According to the question:
Algebra of functions:
Algebra of functions means the operations of the functions, specifically the arithmetic operations. Algebra of functions mainly deals with the following four arithmetic operations of functions:
Addition of functionsSubtraction of functionsMultiplication of functionsDivision of functionsThe function given as:
f(x) = -3x, g(x) = 2x-1 are the two functions
then by the algebra of two functions(adding two functions) we can find the value of 3f(x) + 2g(x)
Now find
3f(x) = 3(-3x) = -9x -----------(i)
2g(x) = 2(2x-1)
= 2(2x)-2(1)
2g(x) = 4x-2 ----------(ii)
Now, add the above two equation (i) and (ii)
3f(x) + 2g(x) = -9x + 4x - 2
= -5x-2
Learn more about Algebra of function at:
https://brainly.com/question/28841704
#SPJ4
The given question is incomplete, complete question is:
Let f(x) = -3x and g(x) = 2x-1
Find the following: 3f(x) +2g(x)
0 6x +4
0 -5x - 2
O There is no correct answer given.
O 8x -8
O 5x+1
Bodin Company manufactures finger splints for kids who get tendonitis from playing video games. The firm had the following inventories at the beginning and end of the month of January. Jan 1 Jan 31 Finished goods$125,000 $117,000 Work in process 233,000 251,000 Raw material 133,000 124,000 The following additional data pertain to January operations. Raw material purchased$190,000 Direct labor 350,000 Actual manufacturing overhead 170,000 Actual selling and administrative expenses 110,000 The company applies manufacturing overhead at the rate of 60 percent of direct-labor cost. Any overapplied or underapplied manufacturing overhead is accumulated until the end of the year. Compute the company's prime cost for January.
Answers
The company's prime cost for January is 556000.
As per the data given:
Bodin Company manufactures finger splints for kids who get tendonitis from playing video games.
The firm had the following inventories at the beginning and end of the month of January.
January 1 January 31
Finished goods---------$125,000----------------$117,000Work in process--------$233,000---------------$251,000Raw material-------------$133,000----------------$124,000The following additional data pertain to January operations.
Raw material purchased------------------------------------$190,000Direct labor------------------------------------------------------350,000 Actual manufacturing overhead--------------------------170,000Actual selling and administrative expenses----------110,000Here we have compute the company's prime cost for January.
First add Raw materials, January 1 with Raw materials purchased and then subtract Raw materials, January 31 from this sum and then later add up the Direct labor to the result.
The final result will be the prime cost for January
Raw materials, January 1_______133000(+) Raw materials purchased____190000(-) Raw materials, January 31____117000Raw materials used___________206000(+) Direct labor______________ 350000Prime cost__________________556000Therefore the prime cost is 556000.
For more questions on the prime cost
https://brainly.com/question/18270480
#SPJ4
please help!!!!!
solve inequalities

Answers
Answer:
area of rectangle is given by L×B
12(2x-3)>60
24x-36>60
24x>60+36
24x>96
\( \frac{24x}{24} > \frac{96}{24} \\ x > 4\)
x is all the numbers greater than 4
N.b with 4 NOT INCLUDED
The area of a rectangle is 110.33 cm. The length of the rectangle is 11.8 cm Work out an estimate for the width of the rectangle.
Answers
Area of rectangle = l × b = 110.33 cm²
= 11.8 × b = 110.33
\( = b = \frac{110.33}{11.8} \\ b = 9.35\)
Solve the following system of equations with NR Method U = 2x^2 + 3y - 4 V = y + sin(x)
Answers
To solve the system of equations U = 2x^2 + 3y - 4 and V = y + sin(x) using the Newton-Raphson method, we need to first define our initial guess for x and y. Let's start with x = 1 and y = 1.
Next, we need to find the partial derivatives of U and V with respect to x and y:
dU/dx = 4x
dU/dy = 3
dV/dx = cos(x)
dV/dy = 1
Using these partial derivatives, we can set up the following equations for our iteration process:
x(n+1) = x(n) - (dU/dx*dV/dy - dV/dx*dU/dy)^-1 * (V - V(x(n),y(n)))
y(n+1) = y(n) - (dU/dx*dV/dy - dV/dx*dU/dy)^-1 * (U - U(x(n),y(n)))
Plugging in our initial guess values and solving, we get:
x(1) = 1 - (4*1*1 - cos(1)*3)^-1 * (1 + sin(1) - (2*1^2 + 3*1 - 4))
= 0.7725
y(1) = 1 - (4*1*1 - cos(1)*3)^-1 * (2*0.7725^2 + 3*1 - 4 - sin(0.7725))
= 0.3402
Using these values as our new guess, we can repeat the process until we reach a desired level of accuracy.
Note: The Newton-Raphson method may not always converge to a solution, depending on the specific system of equations and initial guess values used.
To solve the given system of equations using the Newton-Raphson (NR) method, we first need to set up the system in a more suitable form. The given equations are:
1. U = 2x^2 + 3y - 4
2. V = y + sin(x)
We want to find the values of x and y that satisfy both equations simultaneously. The Newton-Raphson method is iterative and requires partial derivatives. We first rewrite the equations as:
F(x, y) = 2x^2 + 3y - 4 - U = 0
G(x, y) = y + sin(x) - V = 0
Now, we calculate the partial derivatives:
∂F/∂x = 4x
∂F/∂y = 3
∂G/∂x = cos(x)
∂G/∂y = 1
Next, we set up the iteration formula using the inverse Jacobian matrix:
[x_n+1] = [x_n] - J^(-1) * [F(x_n, y_n), G(x_n, y_n)]^T
where J^(-1) is the inverse Jacobian matrix:
J^(-1) = 1/((4x)(1) - (3)(cos(x))) * | 1 -cos(x) |
| -3 4x |
To apply the NR method, choose initial values for x and y (x_0, y_0), and iterate the above formula until the solution converges. Keep in mind that the NR method can be sensitive to the initial values chosen, and may not converge in all cases. If it doesn't converge, you might need to try different initial values or use another numerical method.
Visit here to learn more about equations : https://brainly.com/question/29538993
#SPJ11
Use indicator random variables to compute the expected value of the sum of n dice.
Answers
The expected value of the sum of n dice is E[X] = 3.5n.
Indicator random variables are a probability theory tool. They are used to help evaluate probabilities for a given random variable.
Let X be the total number that results from n throws of a fair six-sided die.
By linearity of expectation,E[X] = E[X1 + X2 + ... + Xn] = E[X1] + E[X2] + ... + E[Xn]
Where Xj is the number obtained on the jth die roll.
Each Xi is a discrete random variable with a uniform distribution on the set {1, 2, 3, 4, 5, 6}.
To evaluate E[Xi], we define an indicator random variable Yi as follows: Yi = 1 if Xi = i and Yi = 0 otherwise.
Then, Xi = 1Y1 + 2Y2 + 3Y3 + 4Y4 + 5Y5 + 6Y6.
Thus,E[Xi] = E[1Y1 + 2Y2 + 3Y3 + 4Y4 + 5Y5 + 6Y6] = E[1Y1] + E[2Y2] + ... + E[6Y6] = 1P(Xi = 1) + 2P(Xi = 2) + ... + 6P(Xi = 6) = (1 + 2 + ... + 6) / 6 = 3.5.
Therefore, E[X] = E[X1] + E[X2] + ... + E[Xn] = 3.5n.
Thus, we have computed the expected value of the sum of n dice using indicator random variables. The expected value of the sum of n dice is E[X] = 3.5n.
To know more about expected value, click here
https://brainly.com/question/28197299
#SPJ11
HELP PLZ MATH dasfhadfsbahkfa

Answers
12x=180
/12 /12
X= 15
The answer is B
if its assumptions are met, the analysis of variance technique is appropriate when ____.
Answers
Answer:
comparing the means of three or more groups
Step-by-step explanation:
On Tuesday, it snowed 15 inches in 6 hours. On Friday, it snowed 30 inches in 8 hours. On which day did it snow at a greater rate each hour? How much more per hour? please answer asap
Answers
Answer: Friday, 1.25 more per hour
Step-by-step explanation: if we take the inches it snowed and divide it by the hours, we get the rate of snowfall for one hour. 15/6=2.5 and 30/8=3.75
To get how much more we take the bigger snowfall per hour minus the smaller snowfall per hour 3.75-2.5=1.25
You have a bag with 12 jelly beans in it 4 red 2 black 5 yellow and 1 pink what is the probability of not picking a black one
Answers
Answer:
\(\boxed {\boxed {\sf \frac{5}{6} \ or \ 0.833}}\)
Step-by-step explanation:
Probability can be found by dividing the favorable outcomes by the total outcomes.
\(P=\frac{favorable \ outcomes}{total \ outcomes}\)
In this problem, a favorable outcome is not picking a black jelly bean. The total outcomes is the total number of jelly beans.
\(P( \ not \ black \ jelly \ bean)=\frac{not \ black \ jelly \ beans}{all \ jelly \ beans}\)
There are 10 jelly beans that are not black (4 red+5 yellow + 1 pink =10) There are 12 total jelly beans (4 red+ 2 black+ 5 yellow + 1 pink= 12)\(P( not \ black \ jelly \ bean )=\frac{10}{12}\)
This fraction can be reduced. Both the numerator and denominator can be divided by 2.
\(P(not \ black \ jelly \ bean)=\frac{10/2}{12/2}\)
\(P(not \ black \ jelly \ bean)=\frac{5}{6}\)
Probabilty can also be written as a decimal.
\(P(not \ black \ jelly \ bean)=0.833\)
The probabilty of not picking a black jelly bean is 5/6 or 0.833
The number of dimes you have is three times your number of quarters. You have $3.85. How many dimes do you have?
Answers
Answer:
You have
21
dimes and
7
quarters.
Explanation:
Let
x
be the number of quarters, and
3
x
the number of dimes.
The amount of money you have can be written as
0.25
x
+
0.1
⋅
3
x
=
3.85
.
Now isolate
x
to find the number of quarters:
0.25
x
+
0.1
⋅
3
x
=
3.85
0.25
x
+
0.3
x
=
3.85
0.55
x
=
3.85
x
=
3.85
0.55
=
7
=
the number of quarters.
Then multiply by three to get the number of dimes:
7
⋅
3
=
21
7
⋅
$
0.25
+
21
⋅
$
0.1
=
$
3.85
Step-by-step explanation:
Hope this helped
PLEASE ANSWER! 5 STAR RATING - THANKS (PROFILE TOO) - BRAINLIEST IF I CAN
Each year, a school sends 50 students to a
conference.
Last year, the cost was $12.50 per student.
This year, the cost per student has increased
by 16%.
What is the total cost to send 50 students to
the conference this year?
a $625
b $633
c $725
d $841
Answers
Answer:
c) $725
Explanation:
Last year price: $12.50
If increased by 16%, 100% + 16% = 116%
116% * $12.50
$14.5, each student
Total cost for all 50 students
$14.5 * 50
$725
x² + 2xy ty = 144
(x+y)³= ?
Answers
Answer:
t=144x3+432x2y+432xy2+144y3−x2
2xy2
Step-by-step explanation:
