Answers
Answer & Step-by-step explanation:
When we see the phrase "rate of change" then it means that we are looking for the slope. So, we will need to know the formula for finding slope or the rate of change.
\(slope=\frac{y_2-y_1}{x_2-x_1}\)
Now, let's use this equation to solve for the rate of change of each question.
Problem 1:
\(Slope=\frac{2-\frac{4}{3}}{0-(-1)}\\\\Slope=\frac{\frac{2}{3}}{1}\\\\Slope=\frac{2}{3}\)
The rate of change of this equation is 2/3
Problem 2:
\(Slope=\frac{4-2}{1-0}\\\\Slope=\frac{2}{1}\\\\Slope=2\)
The rate of change for this equation is 2
Problem 3:
\(Slope=\frac{10-4}{2-1}\\\\Slope=\frac{6}{1}\\\\Slope=6\)
The rate of change for this equation is 6
Related Questions
Lucky 7 Lottery tickets have a sequence of 7 digits, allowing for repeats. (a) How many tickets are possible? (b) How many tickets are possible without repeats? (c) How many tickets are possible such that no two adjacent digits are the same? (d) How many tickets are there that either begin with 1-2-3 or 7-6 ?
Answers
There are 2,000,000 tickets that either begin with 1-2-3 or 7-6.
Lucky 7 Lottery tickets have a sequence of 7 digits, allowing for repeats. The given problem requires to find out the possible number of lottery tickets that can be made based on the given conditions.
a. How many tickets are possible? Each number in the ticket can have 10 possibilities (0-9).
The total number of tickets possible is found by multiplying the possibilities of each number together.
Therefore, the total number of tickets that are possible is:10 × 10 × 10 × 10 × 10 × 10 × 10 = 10⁷.
Hence, there are 10,000,000 possible tickets.
b. How many tickets are possible without repeats? Without repeats means each number must be unique. In the first selection, there are ten possible numbers. In the second selection, there are nine possible numbers remaining (since the first digit can’t be repeated), and so on.
Therefore, the total number of tickets that are possible without repeats is:10 × 9 × 8 × 7 × 6 × 5 × 4 = 604,800.
c. How many tickets are possible such that no two adjacent digits are the same?There are 10 options for the first digit. However, for the second digit, there are only nine options available since it cannot be the same as the first.
The third digit can't be the same as the second, so there are nine options. This continues for all digits of the ticket.
Therefore, the total number of tickets that are possible with no adjacent digits the same is:10 × 9 × 9 × 9 × 9 × 9 × 9 = 531441.
d. How many tickets are there that either begin with 1-2-3 or 7-6
There are two sets of 7 digit numbers which begin with 1-2-3:1-2-3-x-x-x-x,
where x can be any of the 10 digits0-1-2-3-x-x-x, where x can be any of the 10 digits.
Therefore, the total number of tickets that either begin with 1-2-3 or 7-6 is:2 × 10 × 10 × 10 × 10 × 10 × 10
= 2,000,000.
To know more about tickets visit:
https://brainly.com/question/183790
#SPJ11
Name the intersection of plane P and line m.
F. Line n
G. Point A
H. AC
J. Segment AE

Answers
Answer:
the answer is segment AE
I do not understand this/ help me answer these

Answers
Answer:
-6b -6c3w -122x -246 + 3r8y - 16xStep-by-step explanation:
A study was conducted by a team of college students for the college research center. From the study, it was reported that most shoppers have a specific spending limit in place while shopping online. The reports indicate that men spend an average of $230 online before they decide to visit a store. If the spending limit is normally distributed and the standard deviation is $19.
(a) Find the probability that a male spent at least $210 online before deciding to visit a store. Ans: ____________
(b) Find the probability that a male spent between $240 and $300 online before deciding to visit a store. Ans: ____________
(c) Find the probability that a male spent exactly $250 online before deciding to visit a store. Ans: (d) Ninety-one percent of the amounts spent online by a male before deciding to visit a store are less than what value? Ans: ____________
Answers
Answer:
0.8536
0.29933
Step-by-step explanation:
Given :
Mean amount spent, μ = $230
Standard deviation, σ = $19
1.)
Probability of spending atleast $210
P(x ≥ 210)
The Zscore = (x - μ) / σ = (210 - 230) / 19 = - 1.052
P(Z ≥ -1.052) = 1 - P(Z ≤ - 1.052) = 1 - 0.1464 = 0.8536
2.)
Probability that between $240 and $300 is spent:
P(x < $240) = Zscore = (240 - 230) / 19 = 0.526
P(Z < 0.526) = 0.70056
P(x < 300) = Zscore = (300 - 230) / 19 = 3.684
P(Z < 3.684) = 0.99989
P(Z < 3.684) - P(Z < 0.526)
0.99989-0.70056 = 0.29933
.
A person invests 10000 dollars in a bank. The bank pays 5.5% interest compounded
monthly. To the nearest tenth of a year, how long must the
person leave the
in the bank until it reaches 27400 dollars?
leave the money
r
A = P(1 + -)nt
n
Answers
Answer:
The answer is 18.4 months.
suppose the linear production function for a firm is given by:q = f(k,l,) = 3k 2l.if the firm employs 3 machines and 5 workers, output is equal to
Answers
Answer:
Step-by-step explanation:
Q = F(K,L) = 3K+2L.
HELP!!!! I NEED TO SUBMIT THIS WITHIN 3 HOURS!!!!!!
At a dinner party, two desserts are being served. Six of the guests choose cheesecake, and eight of the guests choose apple pie. Write two associated part-to-whole ratios for this situation, in simplest form. Then, interpret these ratios within the situation.
Answers
Answer:
6:8, 3:4
hope this helps, im not sure if im correct tho sorry
Step-by-step explanation:
roslyn has twenty boxes. thirteen of the boxes contain pencils, nine of the boxes contain pens, and three of the boxes contain neither pens nor pencils. how many boxes contain both pens and pencils?
Answers
The number of boxes containing both pens and pencils is 2.
What is set?
A set is defined as a well-defined collection of distinct objects. It is denoted by the capital letters of the English alphabet. Its value remains the same for every individual.
Calculation for the number of boxes containing both pens and pencils
Total number of boxes is given by the union of two sets A and B; i.e. A∪B= 20
Boxes having pencils is given by the set A = 13
Boxes having pens is given by the set B = 9
Boxes having neither pens nor pencils, A'∩B' = 3
Boxes containing both pens and pencils are given by the intersection of the sets, A∩B
A∩B = A + B - A∪B
= 13 + 9 - 20
= 2
Hence, the number of boxes containing both pens and pencils is 2.
To learn more about sets, visit here:
https://brainly.com/question/24462379
#SPJ4
solve for x x/8 -7 = -6
Answers
Answer:
x = 8
Step-by-step explanation:
Answer:
x=-8
Step-by-step explanation:
solve for x by simplifying both sided of the equation then isolating the variable
swer.
At the beginning of the month, Sarah had $600 in her bank account. Within the month she
made two deposits of $40 and $25. She also made three withdrawals of $100, $50, and $20.
How much was in her account at the end of the month?
Answers
Sarah have $495 in her account at the end of the month.
Given,
The amount Sarah had in her bank account at the beginning of the month = $600
The deposits she made within the month = $40 and $25
The withdrawals she made = $100, $50 , $20
We have to find the balance amount in Sarah's account after all these transactions made:
The deposits Sarah had = 600 + 40 + 25 = 665
Sarah had $665 in her account in a month.
Withdrawals made by Sarah = 100 + 50 + 20 = 170
Sarah made a total withdrawal of $170 in the month.
Now, we have to find the account balance of Sarah:
Account balance = Total deposits - Total withdrawals
Account balance = 665 - 170 = 495
That is, Sarah have $495 in her account at the end of the month.
Learn more about account balance here: https://brainly.com/question/23008152
#SPJ1
Give an example of a pyramid and a prism that have the same base and the same volume. Explain your reasoning.
Answers
An example of a pyramid and a prism that have the same base and volume is a triangular pyramid and a triangular prism with congruent bases and heights.
Let's consider a triangular pyramid and a triangular prism with congruent bases and heights. Both shapes have a triangular base, meaning their base area is the same. The volume of a pyramid is given by the formula V = (1/3) * base area * height, whereas the volume of a prism is calculated as V = base area * height.
Since the bases of the pyramid and prism are congruent, their base areas are equal. In order for the pyramid and prism to have the same volume, the height of the pyramid must be three times the height of the prism. This is because the volume of a pyramid is one-third of the volume of a prism with the same base and height.
By choosing a triangular pyramid and a triangular prism with congruent bases and heights, we ensure that the base area and the height are the same for both shapes. Therefore, their volumes will also be equal.
Learn more about congruent here: https://brainly.com/question/29116501
#SPJ11
please help me with part two

Answers
Answer: 17
Step-by-step explanation:)
Find f/(x). (a) f(x) = xsinx (b) f(x) = sech-1x²
Answers
The derivative of f(x) = sech^(-1)(x^2) is f'(x) = 2x/sqrt(1 - x^4).
a) To find f'(x) for f(x) = x*sin(x), we can use the product rule and the derivative of the sine function.
Using the product rule, we have:
f'(x) = (xsin(x))' = xsin'(x) + sin(x)*x'
The derivative of sin(x) is cos(x), and the derivative of x with respect to x is 1. Therefore:
f'(x) = x*cos(x) + sin(x)
So, the derivative of f(x) = xsin(x) is f'(x) = xcos(x) + sin(x).
(b) To find f'(x) for f(x) = sech^(-1)(x^2), we can use the chain rule and the derivative of the inverse hyperbolic secant function.
Let u = x^2. Then, f(x) can be rewritten as f(u) = sech^(-1)(u).
Using the chain rule, we have:
f'(x) = f'(u) * u'
The derivative of sech^(-1)(u) can be found using the derivative of the inverse hyperbolic secant function:
(sech^(-1)(u))' = 1/sqrt(1 - u^2)
Since u = x^2, we have:
f'(x) = 1/sqrt(1 - (x^2)^2) * (x^2)'
Simplifying:
f'(x) = 1/sqrt(1 - x^4) * 2x
So, the derivative of f(x) = sech^(-1)(x^2) is f'(x) = 2x/sqrt(1 - x^4).
learn more about derivative here
https://brainly.com/question/29144258
#SPJ11
Please help I beg of y’all

Answers
Answer:
I think its 180
Step-by-step explanation:

Because AB is parallel to CD, alternate (Z) angles are equal, so the angle to the right of ACB = 46. Angles on a straight line add to 180, so 180 - 46 - 65 = 69.
Brandon rolls a six sided die twenty times, and records the result in the table below. how many times did brandon roll above the average? 6 1 3 4 4 4 6 5 5 3 6 4 4 5 2 3 5 4 4 2 a. 14 b. 7 c. 5 d. 4
Answers
The average is the arithmetic mean of all the observations of a set of numbers. The number of times Brandon rolls above the average is 7.
What is average?The average is the arithmetic mean of all the observations of a set of numbers. it is found by dividing the sum of all the observations of the set by the number of observations in the set.
\(\rm{Average=\dfrac{Sum\ of\ observations}{Number\ of\ observations}\)
In order to know the number of times Brandon rolls the dice above the average, we first need to calculate the average of the twenty rolls.
The average of the 20 times dice rolls,
\(\rm Average = \dfrac{6+1+3+4+4+4+6+5+5+3+6+4+4+5+2+3+5+4+4+2}{20}\)
\(\rm Average = \dfrac{80}{20} = 4\)
Thus, the average of the 20 rolls of the dice is 4.
Now, the number of times the result of the dice roll is above 4(x>4) is 7.
Hence, the number of times Brandon rolls above the average is 7.
Learn more about Average:
https://brainly.com/question/2426692
The ratios of corresponding sides in the two triangles
are equal.
What other information is needed to prove that AFGE
- AIJH by the SAS similarity theorem?
PLEAS HELP?
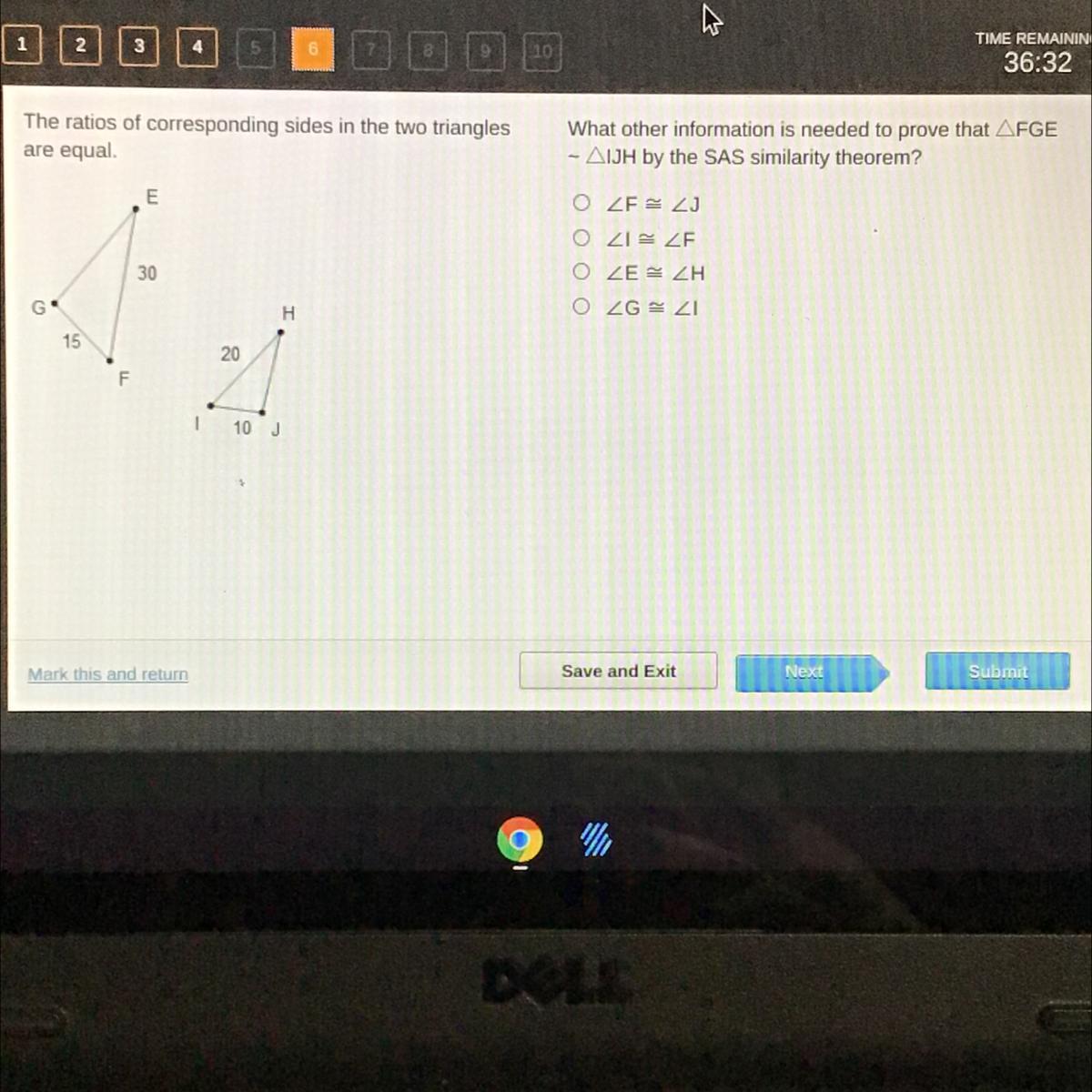
Answers
Answer:
2nd Choice
Step-by-step explanation:
because in SAS, we use 2 sides and the angle between them
The part used to prove the triangles are similar using SAS similarity is
<I = <F.
What is Similarity?If the proportion of the two sides of one triangle is the same as the proportion of the two sides of another triangle, and the angle inscribed by the two sides of both triangles is equal, two triangles are said to be similar.
The three-sided polygon is the triangle. The following is the criteria for triangle similarity:
Corresponding angles of both triangles are equal, corresponding sides of both triangles are proportional to each other.To prove for SAS similarity, we need ratio of two corresponding sides of two triangles equal.
and, one angle which is in between the sides used for ratio.
As, ratios of corresponding sides in the two triangles are equal.
FG / IJ = GE / JH = EF / IH
So, the angle will be <I = <F.
Learn more about Similarity here:
https://brainly.com/question/26451866
#SPJ7
How to do this question plz answer me step by step plzz plz plz plz plz plz plz plz

Answers
Answer:
288.4m
Step-by-step explanation:
This track is split into a rectangle and two semi-circles.
We can find the length of the semi-circles by finding its circumference with the formula \(2\pi r\).
\(2\cdot3.14\cdot30\\188.4\)
However this is half a circle, so:
\(188.4\div2=94.2\).
There are two semi-circles.
\(94.2\cdot2=188.4\)
Since there are two legs of 50m each, we add 100 to 188.4
\(188.4+100=288.4\)m
Hope this helped!
Answer:
Step-by-step explanation:
To solve for the perimeter, we first look at the rectangle in the middle. the length is 50m, and there are two sides to it, so: 50 * 2 = 100m for the top and bottom of the track.
For the circle, we can see the diameter is 30m. To solve for the circumference, we need to use the formula 2πr.
15 * 2π ≈ 94.2477796077
We add that to 100m and get:
194.2477796077
Callan knows that the area of a square piece of artwork he owns is 289 square inches. Which shows the correct step he should take if he wants to find out the side lengths of the piece of artwork?.
Answers
Answer:
One side length is 17. Because you square root 289 to figure out the side length.
Step-by-step explanation:
The area of a square is a side length * a side length
or l^2 = 289
sqrt or 289 = 17
Help me please I am literally dying right now

Answers
Answers with Explanation:
12. In the picture we saw that there are 3 pears, if one of the factors is \(\frac{1}{2}\)
then we know that the other factor is 6 because \(6 * \frac{1}{2}\) is equal to 3.
So the equation is:
\(6 * \frac{1}{2} = 3\)
13. How you could get the answer for \(45 * \frac{7}{9}\) mentally? Well, you only need to divide 45 by 9 and then multiply the answer by 7.
So:
45 ÷ 9 = 5
5 × 7 = 35
14. If 2.99 - 1 is equal to 1.99 that means that is less.
Explanation:
\(2.99-1=1.99\) (that means that is less than 3)
Hope this helps :)
Pls brainliest...
What are the solutions of the system? {y=6x 6y=−x2 5x 6.
Answers
The solutions of the system are the values of x that satisfy the quadratic equation x^2 - 31x + 6 = 0.
The system of equations is: {y = 6x
{6y = -x^2 + 5x + 6
To find the solutions of the system, we need to solve these two equations simultaneously.
First, we'll substitute the value of y from the first equation into the second equation:
6(6x) = -x^2 + 5x + 6
36x = -x^2 + 5x + 6
Rearranging the equation to a quadratic form:
x^2 - 31x + 6 = 0
To solve this quadratic equation, we can use factoring, completing the square, or the quadratic formula. However, the roots of this equation do not result in nice whole numbers or simple fractions.
Learn more about quadratic equation here: brainly.com/question/30098550
#SPJ11
pls help i need help

Answers
Answer: b is correct the one you have selected is right!
Step-by-step explanation:
plz mark brainliest
Find the slope of the line.

Answers
Answer:
-1/3
Step-by-step explanatition
the slope goes down to the right, so it is negitive. It goes down x by 3, and down y by 1. slope = y/x , slope = -1/3
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!5

Answers
Answer:
A is the best answer to give
BRAINLIST ???
Answer:
C a line that shows the set of all solutions to the equation
Step-by-step explanation:
y = -4x+7 is the slope intercept form of a line
The slope is -4 and the y intercept is 7
the capacities (in ampere-hours) of 10 batteries are 140, 136, 150, 144, 148, 152, 138, 141, 143, 151. (a) estimate the population variance σ2. (b) compute a 99 percent two-sided confidence interval for σ2.
Answers
The population variance of the capacities is 30.76
the capacities (in ampere-hours) of 10 batteries are 140, 136, 150, 144, 148, 152, 138, 141, 143, 151.
The number of observations n = 10
mean = (x₁ + x₂ + x₃.....x₁₀)/10
mean = (140 + 136 + 150 + 144 + 148 + 152 + 138+ 141 + 143 + 151)/10
mean = 1443/10 = 144.3
variance = ∑(x - mean)²/(n - 1)
variance = ((140 - 144.3)² + (136 - 144.3)² + (150 - 144.3)² + (144- 144.3)² + (148 - 144.3)² + (152 - 144.3)² + (138 - 144.3)² + (141-144.3)² + (143 - 144.3)² + (151 - 144.3)²)/(10 - 1)
variance = 276.9/9 = 30.76
Therefore, the population variance of the capacities is 30.76
To learn more about variance refer here
https://brainly.com/question/25639778
#SPJ4
The product of 3 and a number, divided by 9
Answers
Answer:
\( \frac{3(n)}{9} \: or \: 3n \div 9 \)
Step-by-step explanation:
\( \frac{3(n)}{9} = \frac{3n}{9} \)
The number is 'n'.
Hope this helps ;) ❤❤❤
Write an inequality using variables x and y whose graph is described by the given information. The points (2,5) and (-3,-5) lie on the boundary line. The points (6,5) and (-2,-3) are solutions of the inequality.
Answers
The inequality using variables x and y which satisfy the points are; y>-3x+3.
What is inequality?Inequality is defined as the relation which makes a non-equal comparison between two given functions.
Given that the points (2,5) and (-3,-5) lie on the boundary line.
The system of inequality is given by:
y>-3x+3-
Now, the point that will lie in the solution set to the following system of inequality are the point that satisfies the inequality.
a) (6, 5)
when x=6 and y= 5
then we have:
y>-3x+3
6 > -3×5 + 3
6>- 15+3
5 > -12
This means that the point will lie in the solution set.
Also, (-2, -3) when x= -2 and y= -3
then we have:
5 > -3×(-2) + 3
5> 6 + 3
5> 9
Hence, the inequality using variables x and y which satisfy the points are; y>-3x+3.
Learn more about inequality ;
brainly.com/question/14164153
#SPJ1
a ladder 10 feet long rests against a vertical wall. let be the angle between the top of the ladder and the wall, and let be the distance from the bottom of the ladder to the wall. if the bottom of the ladder slides away from the wall, how fast does change with respect to when ?
Answers
Rate of change of x with respect to \(\alpha\) when \(\alpha =\frac{\pi }{3}\) is 5ft/s.
Since the ladder is 10ft long resting against a vertical wall.
Let the angle between the top of the ladder and the wall is \(\alpha\) .
And let the distance from the bottom of the ladder to the wall is x.
Thus we need to find the rate of change of x with respect to \(\alpha\) when \(\alpha =\frac{\pi }{3}\)
Consider L to be the length of the ladder.
Then, L = 10ft
Thus, we get the relation between the angle and distance x i.e.
x = L \(\sin \alpha\)
On differentiating the above equation,
\(\frac{dx}{dt} =L \cos \alpha\)
Now after putting the values \(\alpha =\frac{\pi }{3}\) in above equation, we get,
\(=(10)\cos(\frac{\pi }{3} )=(10)(\frac{1}{2} )=5\)
Therefore, \(\frac{dx}{dt} =5\) ft/s
To learn more about differentiation visit:
https://brainly.com/question/954654
#SPJ4
Evaluate the following expression using the values given. (1 point)
Find 2x2 − 2z4 + y2 − x2 + z4 if x = −4, y = 3, and z = 2.
Answers
The value of the expression \(2x^2 - 2z^4 + y^2 - x^2 + z^4\), when x = -4, y = 3, and z = 2, is 9.
To evaluate the expression\(2x^2 - 2z^4 + y^2 - x^2 + z^4\) using the given values of x = -4, y = 3, and z = 2, we substitute these values into the expression:
\(2x^2 - 2z^4 + y^2 - x^2 + z^4 = 2(-4)^2 - 2(2)^4 + (3)^2 - (-4)^2 + (2)^4\)
First, let's simplify the exponents:
\(2(-4)^2 = 2(16) = 32\)
\(2(2)^4 = 2(16) = 32\\(-4)^2 = 16\\(2)^4 = 16\)
Now, we substitute these simplified values back into the expression:
\(2x^2 - 2z^4 + y^2 - x^2 + z^4 = 32 - 32 + 9 - 16 + 16\)
Next, we perform the addition and subtraction operations:
32 - 32 + 9 - 16 + 16 = 0 + 9 - 16 + 16
Continuing with the operations:
0 + 9 - 16 + 16 = 9 - 16 + 16
Further simplification:
9 - 16 + 16 = -7 + 16
Finally, we perform the addition:
-7 + 16 = 9
Therefore, the value of the expression \(2x^2 - 2z^4 + y^2 - x^2 + z^4,\)when x = -4, y = 3, and z = 2, is 9.
By substituting the given values into the expression and performing the necessary calculations, we find that the result is 9. It's important to carefully substitute the values and follow the order of operations to obtain the correct answer.
for more such question on expression visit
https://brainly.com/question/1859113
#SPJ8
find the first term 43, 39, 35, 31, 27,
Answers
Answer:
23
Step-by-step explanation:
the difference between each number in the sequence is 4. Taking 4 away from 27 gives you 23
Hope this helps!
I need help finding the equation and graphing it.

Answers
Step-by-step explanation:
First find the slope with the equation y/x
80/50=8/5 (you want this in fraction form)
y-80=8/5(x-50)
y-80=8/5x-80
y=8/5x+0
the y-intercept is zero (so place a dot at the origin)
next, go up 8 values and then 5 to the right (5,8), continue to do this process until you have enough points to graph a line. (10,16), (15,24), (20,32)
Hope this helps!
