Answers
Related Questions
please answer all the questions, i’ll mark you as brainlinest

Answers
The statement for the congruency of the triangles and the corresponding sides are as follows:
ΔPQR ≅ ΔCBA∠Q = ∠B∠R = ∠A∠P = ∠CPQ = BCQR = ABHow to find the corresponding sides of congruent triangles?Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal .
In other words, triangles that have exactly the same size and shape are called congruent triangles.
Let's write a congruency statement for the triangles and identify the pair of congruent corresponding side.
Therefore,
ΔPQR ≅ ΔCBA
Hence,
∠Q = ∠B
∠R = ∠A
∠P = ∠C
PQ = BC
QR = AB
learn more on congruent triangles here: brainly.com/question/15485747
#SPJ1
hii please help i’ll give brainliest if you give a correct answer tysm

Answers
Hello!
\(\large\boxed{4 : 3 \text{ and } 16 : 12}\)
We can go through each answer to verify whether each is equivalent to 8 : 6.
4 : 3 is equivalent to 8 : 6 because reducing the ratio 8 : 6 by a factor of 2 yields 4 : 3.
6 : 8 is not equivalent to 8 : 6 because the ratio is reversed.
16 : 12 is equivalent to 8 : 6 because the ratio is increased by a factor of 2.
10 : 8 is not equivalent to 8 : 6. We can verify this by checking whether each term was scaled equally:
10 ÷ 8 = 1.25
8 ÷ 6 = 1.33. Therefore, they are unequal.
7 : 5 is not equal to 8 : 6 for the same reason.
The only correct choices are:
4 : 3 and 16 : 12.
Help find the volume of the figure in terms of Pi.

Answers
In this case, the radius is equivalent to 2mi and the height is equivalent to 7mi. This means….
r^2=4
h=7
Now plug in the numbers into the formula for the volume of a cone.
1/3•4•7•pi
28/3pi
The answer is 28/3 pi.
Answer:
9.33π
Step-by-step explanation:
the formula to solve for the volume of a cone is V=πr^2 * h/3
r = radius of base (2mi)
h = height (7mi)
plug in the numbers
V=π2^2 * 7/3
V=π4*2.33333333
V=9.33π
Which of the following are true regarding the specific rule of addition and the general rule of addition?
If the events A and B are mutually exclusive, you can use the special rule of addition.
If the events A and B are not mutually exclusive, you can use the general rule of addition.
Answers
Both statements are true. When events A and B are mutually exclusive, meaning they cannot occur simultaneously, you can use the special rule of addition.
If events A and B are not mutually exclusive, meaning they can occur together, you should use the general rule of addition. The specific rule of addition can only be used when dealing with mutually exclusive events, while the general rule of addition can be used for any two events, whether they are mutually exclusive or not. The specific rule of addition states that the probability of either event A or event B occurring is equal to the sum of their individual probabilities, while the general rule of addition states that the probability of event A or event B occurring is equal to the sum of their individual probabilities minus the probability of their intersection (if they are not mutually exclusive).
Learn more about addition here: brainly.com/question/29464370
#SPJ11
help meeeeeeeeeeeeee pleaseee rnnnn rn!!!!!!!!!!!!!!!

Answers
The dimensions of the rectangle whose length and width must have a sum of 70 are 35 cm and 35 cm respectively.
What is rectangle?A rcetangle is a plane shape that has pair of opposite side equal and parallel.
To calculate the dimension of rectangle that will have the maximum area, we find the first derivation of the function representing the area of the rectangle, and then equate it to zero.
f(x) = x(70-x)f(x) = 70x-x²At the maximum area,
df(x)/dx = 0Therefore,
df(x)/dx = 70-2x = 0Solve for x
2x = 70x = 70/2x = 35The dimensions of the rectangle are
Length = 35 cmWidth = (70-35) = 35 cm.Hence, the dimensions of the rectangle are 35 cm and 35 cm respectively.
Learn more about rectangle here: https://brainly.com/question/25292087
#SPJ1
Twice during the assembly, a student is chosen at random to assist with the presentation. after the first student has finished assisting, the student returns to the group and can be chosen a second time. what is the probability that the first student chosen is a senior and the second student chosen is a sophomore?.
Answers
Using it's concept, it is found that the probability that the first student chosen is a senior and the second student chosen is a sophomore is given by:
\(p = \frac{11}{320}\)
What is a probability?A probability is given by the number of desired outcomes divided by the number of total outcomes.
Researching this problem on the internet, we have that there are:
31 juniors, 10 sophomores, 17 juniors, 22 seniors.
Then:
Out of 31 + 10 + 17 + 22 = 80 students, 22 are seniors, hence the probability that the first student is a senior is given by \(p_1 = \frac{22}{80} = \frac{11}{40}\).All students can be chosen again, hence the probability that the second student is a sophomore is given by \(p_2 = \frac{10}{80} = \frac{1}{8}\).The events are independent, hence the probability of both is given by:
\(p = p_1p_2 = \frac{11}{40} \times \frac{1}{8} = \frac{11}{320}\)
More can be learned about probabilities at https://brainly.com/question/14398287
#SPJ1
1500 families were surveyed and following data was recorded about their maids at homes.
Type of maids|Only part time|Only full time|Both|
Number of families|860 | 370 | 250 |
A family is selected at random. Find the probability that the family selected has
(i)Both types of maids (ii) Part time maids (iii)No maids
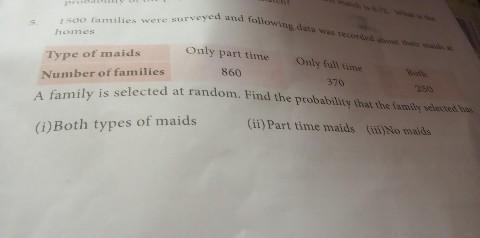
Answers
Explanation:-
Total number of families are surveyed = 1500
Total number of possible outcomes = 1500
Number of part time maids = 860
Number of favourable outcomes to part time maids = 860
Number of only full time maids = 370
Number of favourable outcomes to only full time maids = 370
Number of both type of maids = 250
Number of favourable outcomes to both type of maids = 250
From all families selecting a family randomly is an event then
We know that
Probability of an event =
Number of favourable outcomes/Total number of possible outcomes
1⟩ Probability of getting both type of maids
⇛250/1500
⇛25/150
⇛1/6
Probability of a family has both type of maids= 1/6.
2⟩ Probability of getting Part time maids
= 860/1500
⇛86/150
⇛43/125
Probability of getting Part time maids = 43/125.
3⟩. Number of part time maids =n(P only )=860
Number of only full time maids =n(F only) = 370
Number of both type of maids = n(PnF)= 250
Total number of families are surveyed= n(PUF)
= 1500
number of no maids =
n(PUF)= n(only P)+n(only F)+n(PnF)
= 1500-(860+370+250)
⇛1500-(1480)
⇛20
Number of no maids = 20
Probability of getting no maid = 20/1500
⇛2/150
⇛1/125
Probability of getting no maid = 1/125.
also read similar questions: The queen had 300 servants. there were 10 more butlers than cooks. the number of cooks was twice the number of maids. how many maids worked......
https://brainly.com/question/14999605?referrer
Sally hires a maid to work in her home for $280 per month. The maid is 25 years old and not related to Sally. During 2019, the maid worked 9 months for Sally.Do...
https://brainly.com/question/14701048?referrer
Suppose Mack's wage was $7.00 an hour in 2001 and was $12.00 per hour in 2012. The CPI was 94 in 2001 and 201 in 2012. The 2001 wage in terms of 2012 dollars is
A) $14.97.
B) $14.07.
C) $3.48.
D) $13.16.
E) $7.00.
Answers
The wage of 2001 in terms of wage in 2012 is option A $14.97
Given,
Mack's wages in 2001 = $7 per hour
Mack's wages in 2012 = $12 per hour
The CPI in 2001 = 94
The CPI in 2012 = 201
We have to fins the wage of 2001 in terms of wage in 2012;
CPI;- Consumer Price Index
The CPI is calculated by the Bureau of Labor Statistics each month using a sample of 94,000 prices. To determine the overall change in prices, the index for each good or service is weighted according to its share of recent consumer spending.
Here,
The wage of 2001 in terms of wage in 2012 = (CPI in present year / CPI in past year) x Wage of earlier year
= (201 / 94) x 7
= 14.97
That is,
The wage of 2001 in terms of wage in 2012 is option A $14.97
Learn more about wages here;
https://brainly.com/question/11436134
#SPJ4
evaluate the iterated integral by converting to polar coordinates. 1 0 2 − y2 5(x + y) dx dy y
Answers
We have the iterated integral:
∫
�
=
0
2
∫
�
=
1
5
5
(
�
+
�
)
(
2
−
�
2
)
�
�
�
�
∫
y=0
2
∫
x=1
5
5(x+y)(2−y
2
)dxdy
To convert this to polar coordinates, we need to express $x$ and $y$ in terms of $r$ and $\theta$. Since the region of integration is defined by $0 \leq y \leq 2$ and $1 \leq x \leq 5$, we see that $1 \leq r \leq 5$ and $0 \leq \theta \leq \pi$. Then we have:
�
=
�
cos
�
and
�
=
�
sin
�
x=rcosθandy=rsinθ
The Jacobian of the transformation is $\frac{\partial(x,y)}{\partial(r,\theta)} = r$, so we have:
\begin{align*}
\int_{y=0}^{2} \int_{x=1}^{5} 5(x+y)(2-y^2) ,dx,dy &= \int_{\theta=0}^{\pi} \int_{r=1}^{5} 5(r\cos \theta + r\sin \theta)(2 - r^2\sin^2 \theta) ,r,dr,d\theta \
&= \int_{\theta=0}^{\pi} \int_{r=1}^{5} 10r^2\cos \theta ,dr,d\theta + \int_{\theta=0}^{\pi} \int_{r=1}^{5} 10r^2\sin \theta \cos \theta ,dr,d\theta \
&\quad + \int_{\theta=0}^{\pi} \int_{r=1}^{5} 5r^3\sin \theta ,dr,d\theta - \int_{\theta=0}^{\pi} \int_{r=1}^{5} 5r^5\sin^3 \theta ,dr,d\theta \
&= \int_{\theta=0}^{\pi} \left[ \frac{10}{3}r^3\cos \theta \right]{r=1}^{r=5} ,d\theta + \int{\theta=0}^{\pi} \left[ \frac{5}{2}r^3\sin^2 \theta \right]{r=1}^{r=5} ,d\theta \
&\quad + \int{\theta=0}^{\pi} \left[ \frac{5}{4}r^4\sin \theta \right]{r=1}^{r=5} ,d\theta - \int{\theta=0}^{\pi} \left[ \frac{5}{6}r^6\sin^4 \theta \right]{r=1}^{r=5} ,d\theta \
&= \int{\theta=0}^{\pi} \frac{1240}{3}\cos \theta + \frac{60}{2}\sin^2 \theta + \frac{155}{4}\sin \theta - \frac{2480}{6}\sin^4 \theta ,d\theta \
&= \left[ \frac{1240}{3}\sin \theta - \frac{60}{2}\frac
Learn more about integral at: brainly.com/question/31433890
#SPJ11
Pablo is on a road trip which will cover a distance of 840 miles. He plans to break the trip up and will complete it over three days. The distances and average speeds for the first two days are shown below.Day One: 55 hours at an average speed of 66 miles per hour. Day Two: 55 hours at an average speed of 58 miles per hour. If the average speed on the third day is 55 miles per hour, how many more hours will it take for Pablo to complete his trip?
Answers
Answer: 2.87 hours
Step-by-step explanation:
There may be a typo in the question because 55 hours in a day is not logical so you must have meant 5.5 hours.
In that case, the hours he will require on the third day would require the distance left to calculate. Get this distance from the first 2 days.
Day 1 distance travelled = Time * Speed
= 5.5 * 66
= 363 miles
Day 2 distance travelled = Time * Speed
= 5.5 * 58
= 319 miles
Total distance remaining
:= 840 - 363 - 319
= 158 miles
Travelling at 55 miles per hour, the time to be taken is:
= Distance remaining / Speed
= 158 / 55
= 2.87 miles per hour
Tiya flipped a coin 40 times. The coin landed heads up 16 times and tails up 24 times. Part A: Based on the results, what is the experimental probability of the coin landing heads up
Answers
The experimental probability of the coin landing heads up is calculated by dividing the number of times the coin landed heads up (16) by the total number of flips (40). So the experimental probability of the coin landing heads up is:
P(heads up) = 16/40
Simplifying the fraction by dividing both the numerator and denominator by 8, we get:
P(heads up) = 2/5 or 0.4
Therefore, based on the results, the experimental probability of the coin landing heads up is 0.4 or 2/5.
To find the experimental probability of the coin landing heads up, you'll need to use the following formula:
Experimental probability = (Number of successful outcomes) / (Total number of trials)
In this case, the successful outcome is the coin landing heads up, which occurred 16 times. The total number of trials is 40 flips. So, the experimental probability would be:
Experimental probability (heads up) = (16 successful outcomes) / (40 total flips)
Now, divide 16 by 40 to get the probability:
Experimental probability (heads up) = 16/40 = 0.4 or 40%
So, based on the results, the experimental probability of the coin landing heads up is 40%.
Learn more about Probability here : brainly.com/question/30034780
#SPJ11
use the laplace transform to solve the given initial-value problem. y'' − 4y' 4y = t, y(0) = 0, y'(0) = 1
Answers
The Laplace transform can be used to solve the given initial-value problem, where y'' − 4y' + 4y = t, with initial conditions y(0) = 0 and y'(0) = 1.
To solve the initial-value problem using the Laplace transform, we first apply the transform to both sides of the differential equation. Taking the Laplace transform of the given equation yields:
s^2Y(s) - sy(0) - y'(0) - 4(sY(s) - y(0)) + 4Y(s) = 1/s^2,
where Y(s) represents the Laplace transform of y(t) and s represents the Laplace variable. Substituting the initial conditions y(0) = 0 and y'(0) = 1 into the equation, we have:
s^2Y(s) - 1 - 4sY(s) + 4Y(s) = 1/s^2.
Simplifying the equation, we can solve for Y(s):
Y(s) = 1/(s^2 - 4s + 4) + 1/(s^3).
Using partial fraction decomposition and inverse Laplace transform techniques, we can obtain the solution y(t) in the time domain.
Learn more about Laplace transform here:
https://brainly.com/question/30759963
#SPJ11
Given: 4(x+3)=52 prove: x=10

Answers
Answer:
...I think this was what you needed?...
Step-by-step explanation:
Input 10 as x,
Add everything in your parenthesis,
and then multiply by 4.
On substituting the value of x left-hand side is equal to the right-hand side.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the expression is 4(x+3)=52. To prove put the value of x = 10,
4(x+3)=52
4 ( 10 + 3 ) = 52
4 x 13 = 52
52 = 52
Hence, the expression is true for the value of x = 10.
To know more about an expression follow
https://brainly.com/question/28926100
#SPJ2
40 is 20% of what number? 50 200 250 8
Answers
20% of x=40
20/100*x=40
Then x=400/2 divide and the answer is 200
(20 Points) Write a program that calculates the sum for the following using a loop. The user will provide the values for i and k. Note: The value of i must always be smaller than or equal to the value of k. If the user provides a larger number first, the program must still work. If the user enters a value for k that is less than i, display an error message and continuously ask for proper values (using a loop). ∑ i
k
2x Example Program Run (red is user input): Enter value for i: 0 Enter value for k:3 Summation: 12 Explanation: 2(0)+2(1)+2(2)+2(3)=
0+2+4+6=12
The values for × go from i to k Another Example Program Run (red is user input): Enter value for i: 6 Enter value for k : 3 Error: i cannot be greater than k. Enter value for i: 5 Enter value for k : 2 Error: i cannot be greater than k.
Answers
The calculated summation value with the message "Summation: " preceding it. The program assumes that the user will provide valid numerical inputs (integers) when prompted.
Here's a Python program that calculates the sum using a loop based on the user's input values for `i` and `k`. The program handles cases where `i` is larger than `k` and continuously asks for proper values until valid inputs are provided.
```python
while True:
i = int(input("Enter value for i: "))
k = int(input("Enter value for k: "))
if i <= k:
break
else:
print("Error: i cannot be greater than k.")
summation = 0
for x in range(i, k+1):
summation += 2 * x
print("Summation:", summation)
```
In this program, we use a `while` loop to repeatedly prompt the user for values of `i` and `k`. We convert the inputs to integers using `int()` for numerical comparison. If the condition `i <= k` is satisfied, we break out of the loop; otherwise, an error message is displayed, and the loop continues.
Once we have valid values for `i` and `k`, we initialize the `summation` variable to 0 and use a `for` loop with `range(i, k+1)` to iterate through the values of `x` from `i` to `k` (inclusive). We accumulate the sum by adding `2 * x` to `summation` in each iteration.
Finally, we print the calculated summation value with the message "Summation: " preceding it.
Note: The program assumes that the user will provide valid numerical inputs (integers) when prompted.
Learn more about Summation here
https://brainly.com/question/24495014
#SPJ11
The mean of a sample is Question 28 options: always equal to the mean of the population. always smaller than the mean of the population. computed by summing the data values and dividing the sum by (n - 1). computed by summing all the data values and dividing the sum by the number of items.
Answers
The mean of a sample is computed by summing all the data values and dividing the sum by the number of items.
The mean of a sample is a measure of central tendency of a sample and represents the average value of the sample.The formula for computing the mean of a sample is as follows:μ = (x₁ + x₂ + x₃ + ... + xₙ) / nwhere μ is the mean, x₁, x₂, x₃, ..., xₙ are the data values and n is the number of items in the sample. The mean of a sample is an estimate of the mean of the population from which the sample was taken. If the sample is representative of the population, the mean of the sample will be similar to the mean of the population.
the mean of a sample is not always equal to the mean of the population, especially if the sample is not representative of the population. In addition, the mean of a sample is not always smaller than the mean of the population. Therefore, options A and B are incorrect.On the other hand, option C is incorrect as well because the formula given is for the computation of the sample variance, not the mean. The formula for the sample variance is as follows:s² = ∑(x - μ)² / (n - 1)where s² is the sample variance, x is a data value, μ is the sample mean and n is the number of items in the sample.Option D is correct because it gives the correct formula for computing the mean of a sample.
To know more about dividing visit:
https://brainly.com/question/15381501
#SPJ11
Evaluate the integrals in Exercises 31–56. Some integrals do notrequire integration by parts. ∫(1+2x^2)e^x^2 dx
Answers
The integration of the function ∫(1 + 2x²)\(e^{x} ^{2}\) is -
\($\frac{i\sqrt{\pi}\; erf(ix) }{2} +\) \($\frac{2i\sqrt{\pi}\;erf(ix) }{4} + \frac{xe^{x}^{2} }{2} +C\).
What is integration?Integration is the process of finding the area under the graph of the function f(x), between two specific values in the domain. We can write the integration as -
I = ∫f(x) dx
Given is to integrate the function -
∫(1 + 2x²)\(e^{x} ^{2}\)
We have the function as -
I = ∫(1 + 2x²)\(e^{x} ^{2}\)
I = ∫\(e^{x} ^{2}\) + ∫2x²\(e^{x} ^{2}\)
I = \($\frac{i\sqrt{\pi}\; erf(ix) }{2} +\) \($\frac{2i\sqrt{\pi}\;erf(ix) }{4} + \frac{xe^{x}^{2} }{2} +C\)
Therefore, the integration of the function ∫(1 + 2x²)\(e^{x} ^{2}\) is -
\($\frac{i\sqrt{\pi}\; erf(ix) }{2} +\) \($\frac{2i\sqrt{\pi}\;erf(ix) }{4} + \frac{xe^{x}^{2} }{2} +C\).
To solve more questions on integration, visit the link-
https://brainly.com/question/14405228
#SPJ4
2. 8 × - 11 - 3× + 8
please solve this thankyou!!
Answers
Answer:
-54.8 ( in fraction -274/5)Step-by-step explanation:
2.8 × (-11) - 3 × 8 =
-30.8 - 24 =
-54.8 ( in fraction -274/5)
What is the expression and value of "six less than the quotient of a number and two, increased by ten" when n = 8?
Answers
Answer:
n/2 - 6 + 10
8/2 - 6 + 10
4 - 6 + 10
= 8
Step-by-step explanation:
Answer:
It's B
Step-by-step explanation:
I just took the test, sorry if I didn't come on time.
1/3 x 8 in simplest form
Answers
In mathematics, every integer is a rational number, hence a whole number 8 can be written as 8/1. 1/3 x 8 = 8/3 in fraction form. 1/3 x 8 = 2.6667 in decimal form.
The simplest form is given as 3/8.
What is a fraction?A fraction is a number written in the form a / b, where a and b are integers and b ≠ 0.
The number a is called as the numerator and b is the denominator.
Two fractions can be multiplied by taking the product of their numerators and denominators respectively.
The given expression is 1/3 x 8.
It can be simplified as follows,
1/3 x 8
Write 8 in the fraction form as 8 = 8/1
= 1/3 x 8/1`
Multiply the numerators and denominators to obtain,
(1 x 8)/(3 x 1)
= 8/3
The given expression can be simplified as 8/3.
To know more about fraction click on,
https://brainly.com/question/10354322
#SPJ2
The angle of depression of a rabbit from the top
of a cliff is 24°. After the rabbit hops a distance
of 80 m horizontally towards the base of the cliff,
the angle of depression of the rabbit from the
top of the cliff becomes 32°. Find the height of
the cliff.
Answers
The angle of depression is the angle formed with the horizontal, when an object is viewed below the horizontal level. Thus, the height of the cliff is approximately 123.86 m.
Let the height of the cliff be represented by h, so that:
From the triangle 1, we have:
tan \(32^{o}\) = \(\frac{h}{x}\)
⇒ h = tan \(32^{o}\)*x
h = x tan \(32^{o}\) ............. 1
Also, from the bigger triangle, we have:
tan \(24^{o}\) = \(\frac{h}{80 + x}\)
⇒ h = tan \(24^{o}\) (80 + x) ......... 2
Now equating the expressions for h in equations 1 and 2, we have:
x tan \(32^{o}\) = tan \(24^{o}\) (80 + x)
0.6249x = 0.4452 (80 + x)
= 35.616 + 0.4452x
0.6249x - 0.4452x = 35.616
0.1797 x = 35.616
x = \(\frac{35.616}{0.1797}\)
x = 198.2 m
Substitute the value of x in equation 1;
h = x tan \(32^{o}\)
= 198.2 * 0.6249
= 123.8552
h = 123.86 m
Therefore, the height of the cliff is approximately 123.86 m.
A sketch to this question is attached.
Visit: https://brainly.com/question/23497407

find tr he values of a b and c.The answers are in degrees.

Answers
a = 55°, b = 97°, c = 83°
Explanation:
Larger triangle:
a° + 44° + 28° + 53° = 180° (sum of angles in a triangle)
a + 125 = 180
a = 180 -125
a = 55°
The smaller triangle by the left:
a° + b° + 28° = 180° (sum of angles in a triangle)
55 + b + 28 = 180
83 + b = 180
b = 180 -83
b = 97°
The smaller triangle by the right:
53° + 44° + c° = 180° (sum of angles in a triangle)
97 + c = 180
c = 180 -97
c = 83°
What is the domain and the range

Answers
Answer:
The Domain is X and Range is Y
Step-by-step explanation:
Top values are domain and bottom values are Range
How do you simplify algebraic expressions?
Answers
Answer:
remove parentheses by multiplying factors.
use exponent rules to remove parentheses in terms with exponents.
combine like terms by adding coefficients.
combine the constants.
Step-by-step explanation:
simplify the following without a calculator leave your answer with positive exponents
\((0.008) \frac{2}{3} \)
Answers
alex is running in a clockwise direction around a circular track with radius 60 yards. he runs for 20 minutes at a speed of 4 yards per second. find the shortest distance between their starting point and their ending point measured along the track
Answers
Answer:
100.9 yards
Step-by-step explanation:
One circuit of the track is a distance of ...
C = 2πr = 2π(60 yd) = 120π yd.
At Alex's running rate, the distance covered in 20 minutes is ...
(4 yd/s)(20 min)(60 s/min) = 4800 yd
The number of circuits will be ...
(4800 yd)/(120π yd/circuit) = 40/π circuits ≈ 12.7324 circuits
The last of Alex's laps is more than half-completed, so the shortest distance to his starting point is 13 -12.7324 = 0.2676 circuits,
That distance is (0.2676 circuits)×(120π yd/circuit) ≈ 100.88 yd
The shortest distance along the track to Alex's starting point is about 100.9 yards.
_____
Additional comment
The exact distance is 120(13π-40) yards. The distance will vary according to your approximation for pi. If you use 3.14, this is about 98.4 yards.
what is the vertex of h=-16t^2+29t+6 and its domain and range, and x and y axis?
Answers
Domain = {t | t ∈ ℝ } or (-∞, ∞)
h = 6
Step by step explanation:
The given quadratic function is h = -16t^2 + 29t + 6.
To find the vertex, we can use the formula:
t = -b / 2a
where a = -16 and b = 29 are the coefficients of the t^2 and t terms, respectively.
Substituting the values of a and b, we get:
t = -29 / 2(-16) = 29 / 32
Substituting this value of t into the original equation, we can find the corresponding value of h:
h = -16(29/32)^2 + 29(29/32) + 6 ≈ 13.47
Therefore, the vertex of the parabola is (29/32, 13.47).
The domain of the function is all real numbers because there are no restrictions on the possible input values of t.
To find the range, we can consider that the coefficient of the t^2 term is negative, which means that the parabola opens downward. Therefore, the vertex is the maximum point of the parabola, and the range is all real numbers less than or equal to the y-coordinate of the vertex, which is approximately 13.47.
The x-axis is the set of values where h = 0. We can use the quadratic formula to find the roots of the equation:
-16t^2 + 29t + 6 = 0
The roots are approximately t = -0.15 and t = 1.92. Therefore, the parabola intersects the x-axis at t = -0.15 and t = 1.92.
The y-axis is the set of values where t = 0. Substituting t = 0 into the equation for h, we get:
h = -16(0)^2 + 29(0) + 6 = 6
Therefore, the parabola intersects the y-axis at h = 6.
Please could someone work this out

Answers
2. 56 minutes
:D
Triangle BCD, with vertices B(4,-7), C(6,-8), and D(7,-2), is drawn on the coordinate
grid below.
S
Answer: A =
6
7
D
9
What is the area, in square units, of triangle BCD?
units
Submit Answer
K

Answers
Answer: The area is 6.5
Anson's toy rocket is shown. What is the volume of the rocket? Round to the nearest tenth if necessary.
Answers
Answer:
The answer is below
Step-by-step explanation:
The rocket is made up of square pyramid and a rectangular prism. Hence the volume of the rocket is the sum of the volume of the square pyramid and the volume of the rectangular prism.
Volume of square pyramid = a²h/3
a = base length = 1.1 in, h = height of pyramid = 2.1 in
Volume of square pyramid = a²h/3 = 1.1² * 2.1/3 = 0.847 in³
Volume of rectangular prism = length * breadth * height = 1.1 * 1.1 * 8.2 = 9.922 in³
Volume of rocket = volume of prism + volume of pyramid = 0.847 + 9.922 = 10.769 in³





