PLEASE SHOW YOUR WORK.
Shawn designs a rectangular garden as shown below. He will design both rock sections to have the same width (x).
The area in, square feet, of Shawn’s garden is found be calculating 15(2x + 7). Shawn incorrectly says the area can also be found using the expression 30x + 7.
Describe the error in Shawn’s expression. As part of your explanation, find the difference, in square feet, between the actual area of Shawn’s garden and the area found using his expression.
Answers
Answer:
a) Shawn's error was that he Multiplied 15 by 2x only. He didn't Multiply 15 by 7
b) The difference, in square feet, between the actual area of Shawn’s garden and the area found using his expression is given as
98 square feet
Step-by-step explanation:
The area in, square feet, of Shawn’s garden is found be calculating 15(2x + 7). Shawn incorrectly says the area can also be found using the expression 30x + 7.
The correct area =
15(2x + 7).
= 30x + 105 square feet
The error in Shawn’s expression is
= 15(2x + 7)
= 30x + 7 square feet
Shawn's error was that he Multiplied 15 by 2x only. He didn't Multiply 15 by 7
The difference, in square feet, between the actual area of Shawn’s garden and the area found using his expression is given as
30x + 105 square feet - 30x + 7 square feet
= 30x + 105 - (30x + 7)
= 30x - 30x + 105 - 7
= 98 square feet
Related Questions
please help................ sigh

Answers
The x-intercept of the linear equation in the table is (-5, 0)
What is the x-intercept of the linear equation?Remember that a general linear equation can be written as:
y = a*x + b
Where a is the slope and b is the y-intercept.
If a line passes through two points (x₁, y₁) and (x₂, y₂) then the slope is:
a = (y₂ - y₁)/(x₂ - x₁)
Here we can use the first two points (33, -22) and (52, -33) to get the slope, it gives:
a = (-33 + 22)/(52 - 33) = -11/19
Then the line is:
y = (-11/19)*x + b
To find the value of b we can replace one of the points in the equation, using (33, -22) we willget:
-22 = (-11/19)*33 + b
- 418/19 + 363/19 = v
-55/19 = b
Then the linear equation is:
y = (-11/19)*x - 55/19
And the x-intercept is the value that we have when y = 0, then:
0 = (-11/19)*x - 55/19
55/19 = (-11/19)*x
(55/19)*(-19/11) = x
-55/11 = x
-5 = x
The x-intercept is (-5, 0)
Learn more about linear equations at:
https://brainly.com/question/1884491
#SPJ1
Of people who died in the United States in recent years, 86% were white, 12% were black, and 2% were Asian. (This ignores a small number of deaths among other races.) Diabetes caused 2.8% of deaths among white people, 4.4% among black people, and 3.5% among Asians. What is the probability that a randomly chosen death is a white person who died of diabetes? (Round your answer to three decimal places.)
Answers
The probability that a randomly chosen death is a white person who died of diabetes is 0.024 determined using the law of total probability.
The law of total probability is a fundamental rule that connects marginal probabilities to conditional probabilities and expresses the total probability of an outcome via several distinct events. The rule states that if the probability of an event is unknown, it can be calculated using the known probabilities of several distinct events. It is given by P(A ∩ B) = P(A|B)P(B)
In order to determine the probability of an event (D) with not enough information to calculate it directly, a related event, say W can be taken and use that to calculate the probability for D.
Let the events that a person from a certain race die be denoted as:
P(W) = 0.86; P(B) = 0.12; P(A) = 0.02
Let the events that a person from a certain race dies of diabetes be denoted as:
P(D/W) = 0.0.028; P(D/B) = 0.044; P(D/A) = 0.035
Probability that a randomly chosen death is a white person who died of diabetes
P(W) x P (D/W) = 0.86 x 0.028 = 0.02408 ≈ 0.024
Learn more about The law of total probability:
https://brainly.com/question/29525746
#SPJ4
Does the following set of ordered pairs represent a function?
(2,3) (3,4) (2,5) (5,8)
Answers
Answer:
No
Step-by-step explanation:
In order for a set of ordered pair to be a function all the x values need to be different. In this case we have two of the same x values so this set won't be a function.
Solve step by step for an upvote.
Question 2 Solve the equation (tan a + 2 sin a)/(tan a - 2 sin a) = 3 for 0°< 1< 180° Select your answer
Answers
There are two possible solutions, a = 45° and a = 135°. Therefore, the answer is 45°, 135°.
Given equation is (tan a + 2 sin a)/(tan a - 2 sin a) = 3 for 0°< a < 180°
To solve the equation, we can use the following steps;
Multiply both sides by the denominator to obtain the fraction in the numerator; (tan a + 2 sin a)
= 3(tan a - 2 sin a) Expand the right side by multiplying 3 by both terms inside the parenthesis; tan a + 2 sin a
= 3 tan a - 6 sin a
Add 6 sin a to both sides; tan a + 8 sin a = 3 tan a
Divide both sides by tan a; 1 + 8 sin a/tan a = 3
Rearrange to obtain the form sin a/cos a; 8 sin a/tan a = 3 - 1 8 tan a = 2 cos a
Divide both sides by 2 to obtain; 4 tan a = cos a
Square both sides of the identity sin²a + cos²a = 1
to obtain; cos²a = 1 - sin²a
Substitute sin²a = 1 - cos²a into the previous equation to obtain; 4 tan a = √(1 - cos²a)
Divide both sides by 4; tan a = √(1 - cos²a)/4
Substitute cos a/2 into the above equation to obtain; tan a = √(1 - 4 tan²a)/2
We know that; tan²a + 1 = sec²a
Substitute the above into the previous equation to obtain; tan a = √(1 - 4/sec²a)/2
Substitute sec²a = 1/cos²a; tan a = √(cos²a - 4)/(2cos a)
Using the fact that 0°< a < 180°, we can obtain cos a by dividing both sides of the equation by sec a = 1/cos a and noting the quadrant the solution belongs to.
Substituting into the equation;
tan a = √(cos²a - 4)/(2cos a)cos a
= 1/tan a2cos a = 2/tan a
= √(cos²a - 4)/cos a
Therefore, cos²a - 4
= 4cos²acos²a - 4cos²a - 4
= 0
We can simplify by dividing by 4; cos²a - cos²a - 1 = 0 Cos²a = 1/2
The values of cos a that satisfy this are; a = 45° or a = 135°
There are two possible solutions, a = 45° and a = 135°. Therefore, the answer is 45°, 135°.
To know more about denominator visit:
https://brainly.com/question/32621096
#SPJ11
a postal worker counts the number of complaint letters received by the united states postal service in a given day. identify the type of data collected.
Answers
When a postal worker counts the number of complaint letters received by the united states postal service in a given day, the type of data collected is quantitative.
How to explain the dataQuantitative data is data that can be measured and expressed in numbers. In this case, the number of complaint letters received by the United States Postal Service in a given day can be measured and expressed as a number.
Qualitative data, on the other hand, is data that cannot be measured or expressed in numbers. For example, the contents of the complaint letters would be qualitative data.
Learn more about data on
https://brainly.com/question/26711803
#SPJ1
you decide to watch the wheel k times to make an estimate. in the first experiment, you see r1 odd/even bets being paid before you see a bet not being paid; in the second, r2; and in the third, r3. what is the maximum likelihood estimate of the number of slots on the wheel?
Answers
To determine the maximum likelihood estimate of the number of slots on the wheel, we need to consider the observed number of odd/even bets paid before observing a bet not being paid in each experiment.
Let's denote the number of slots on the wheel as n. The probability of an odd/even bet being paid is 18/n since there are 18 odd or even slots out of n total slots on a standard roulette wheel. The probability of a bet not being paid is 1/n.
The likelihood function L(n) is the probability of observing the given sequence of r1, r2, and r3 odd/even bets being paid before observing a bet not being paid in the three experiments.
Since we want to find the maximum likelihood estimate, we need to find the value of n that maximizes the likelihood function L(n). To simplify the calculations, we can take the logarithm of the likelihood function and find the value of n that maximizes the log-likelihood function ln(L(n)).
Unfortunately, without the specific values of r1, r2, and r3 provided in the question, it is not possible to determine the exact maximum likelihood estimate of the number of slots on the wheel. The solution would involve solving the equations obtained from the log-likelihood function by setting its derivative to zero. The resulting solution would provide the value of n that maximizes the likelihood function based on the observed values of r1, r2, and r3.
Learn more about probability here: brainly.com/question/31828911
#SPJ11
compared to the standard 5% cutoff for statistical significance, a cutoff of 10%:
Answers
A cutoff of 10% for statistical significance is more lenient compared to the standard 5% cutoff.
What is statistical significance?
Statistical significance is a measure used in hypothesis testing to determine whether an observed result is likely to be due to chance or represents a true effect. It indicates the level of confidence that can be placed in the findings of a study or experiment
Compared to the standard 5% cutoff for statistical significance, a cutoff of 10% would be more lenient or less strict.
In statistical hypothesis testing, the significance level, often denoted as alpha (α), represents the threshold below which the p-value must fall to reject the null hypothesis. The commonly used standard cutoff is 5% (or 0.05), which means that if the p-value is less than 0.05, the result is considered statistically significant, and the null hypothesis is rejected.
When the cutoff is increased to 10% (or 0.10), it means that the threshold for statistical significance is relaxed. In other words, a p-value less than 0.10 would now be considered statistically significant, leading to a higher likelihood of rejecting the null hypothesis. This increased cutoff allows for a wider range of p-values to be considered statistically significant, making it easier to detect effects or relationships.
However, it's important to note that a higher cutoff also increases the chances of a Type I error (rejecting the null hypothesis when it is true). This means there is a higher probability of falsely concluding that there is a significant effect or relationship when it may not actually exist.
Choosing the appropriate significance level depends on the specific context, research field, and the consequences of Type I and Type II errors. Lower significance levels, like 5%, are often used to maintain a more stringent standard and reduce the risk of false positives. However, in certain cases, a higher cutoff like 10% may be suitable, such as in exploratory analyses or when the consequences of Type II errors (failing to detect a true effect) are more severe.
To know more about statistical significance visit:
https://brainly.com/question/30389845
#SPJ4
Complete Question:
Compared to the standard 5% cutoff for statistical significance, a cutoff of 10% would be more lenient or less strict?
At first, the price was decreased by 12%, then it was discounted again by an additional 5%. What is the percent of the total discount?
Answers
16.4%
Step-by-step explanation:
Assuming the 5% was taken off of the already-discounted price, then the original price was multiplied by ...
(1 -12%)(1 -5%) = 0.88×0.95 = 0.836 = 1 -16.4%
in which quadrant does angle theta lie if csc theta <0 and cot theta<0?
Answers
Answer:
Quadrant IV (4)
Step-by-step explanation:
I did the test and the other person was wrong.
The quadrant in which angle theta lie if csc theta < 0 and cot theta < 0 exists Quadrant IV (4).
What is meant by Trigonometric Identities?Trigonometric Identities are equality conditions that hold for all possible values of the variables in the equation and use trigonometry functions. There exists numerous unique trigonometric identities that relate a triangle's side length and angle.
Sine, cosine, and tangent are the fundamental three operations in trigonometry. The cotangent, secant, and cosecant functions are derived from these three basic functions. On these functions, all trigonometrical notions exists built.
Trigonometric identities are equality conditions in trigonometry that hold for all values of the variables that appear and are defined on both sides of the equivalence. These exists identities that, geometrically speaking, involve certain functions of one or more angles.
The quadrant in which angle theta lie if csc theta < 0 and cot theta < 0 exists Quadrant IV (4).
To learn more about trigonometric identities refer to:
https://brainly.com/question/7331447
#SPJ2
In each case find the characteristic polynomial, eigenvalues, eigenvectors, and (if possible) invertible matrix P such that P^-1 AP is diagonal. A = [1 2 3 2]
Answers
The given matrix A is a 2x2 matrix.
First, we find the characteristic polynomial by taking the determinant of the matrix A minus λ times the identity matrix I:
|A - λI| =
|1-λ 2 |
| 3 2-λ| = (1-λ)(2-λ) - 2(3) = λ^2 - 3λ - 4
Thus, the characteristic polynomial of A is λ^2 - 3λ - 4.
Next, we find the eigenvalues of A by solving the characteristic polynomial:
λ^2 - 3λ - 4 = 0
(λ - 4)(λ + 1) = 0
Thus, the eigenvalues of A are λ1 = 4 and λ2 = -1.
To find the eigenvectors, we solve the system of linear equations (A - λI)x = 0 for each eigenvalue.
For λ1 = 4, we have:
(1-4)x1 + 2x2 = 0
3x1 - 2x2 = 0
Solving this system, we get the eigenvector x1 = [2, 3] (or any non-zero scalar multiple of it).
For λ2 = -1, we have:
(1+1)x1 + 2x2 = 0
3x1 + 2+1x2 = 0
Solving this system, we get the eigenvector x2 = [-1, 3] (or any non-zero scalar multiple of it).
To find an invertible matrix P such that P^-1 AP is diagonal, we construct the matrix P using the eigenvectors x1 and x2 as its columns. That is,
P = [2 -1; 3 3]
We can verify that P is invertible by calculating its determinant:
|P| = (2)(3) - (-1)(3) = 9
Since |P| is non-zero, P is invertible.
Then, we calculate P^-1:
P^-1 = (1/9)[3 1; -3 2]
Finally, we can check that P^-1 AP is diagonal:
P^-1 AP = (1/9)[3 1; -3 2][1 2; 3 2][2 -1; 3 3]
= (1/9)[12 0; 0 -1][2 -1; 3 3]
= [8/3 -4/3; -3 1]
Thus, we have found the characteristic polynomial, eigenvalues, eigenvectors, and invertible matrix P such that P^-1 AP is diagonal.
For more details about matrix click here:
https://brainly.com/question/29132693#
#SPJ11
A survey is taken of 50 people at a concert. 30
said they did not like the price of parking. If 1200
people went to the concert, about how many were not
happy about the price of parking?
Answers
Answer:
1170 people are not happy of the price of the parking.
Average height of a species of tree (in feet) after a certain number of years Years 1 2 3 4 5 6 7 8 Height 2.1 3.2 6.8 7.3 11.2 12.6 13.4 15.9 What is the correlation coefficient for the set of data
Answers
Answer:
0.989
Step-by-step explanation:
i believe so at least
the composite numbers smaller than 18
Answers
Hello.
A composite number has more than 2 factors; it's divisible by 1, itself, and something else.
Let's find the composite numbers smaller than 18.
The composite numbers are
4, 6, 8, 9, 10, 12, 14, 15, 16.
I hope it helps.
Have a nice day.
\(\boxed{imperturbability}\)
Solve the following system of equations.
3x + 2y - 5 = 0
x= y + 10
ANSWER:
Answers
2 is y = x - 10

Answer:
yes
Step-by-step explanation:
Chris and Josh have a total of 1,800 stamps in their collections, Josh and Jessica have a total of 2,200 stamps, and Jessica and Chris have a total of 2,000. How many stamps in all the three children have?
Answers
Answer: 3000 stamps
Step-by-step explanation:
Given
Chris and Josh have 1800 stamps
Josh and Jessica have 2200 stamps
Jessica and Chris have 2000 stamps
Suppose Chris, Josh, and Jessica have \(x,y, \text{and}\ z\) stamps
\(\therefore x+y=1800\quad \ldots(i)\\\Rightarrow y+z=2200\quad \ldots(ii)\\\Rightarrow z+x=2000\quad \ldots(iii)\\\text{Add (i), (ii), and (iii)}\\\Rightarrow 2(x+y+z)=1800+2200+2000\\\Rightarrow x+y+z=3000\)
Thus, all three have 3000 stamps
How do I do this?pls help someone i need to understand it for a important test tomorrow

Answers
Answer:
1.08915145
Step-by-step explanation:
First of all do 39 x 52, which equals 2028. Then to do the second part of the equation we move the two bottom numbers place value up by one giving us 38 x 49 which is 1862. And then we put 2028 divided by 1862 into our calculators and get the answer as 1.08915145.
A psychologist predicts that entering students with high SAT or ACT scores will have high Grade Point Averages (GPAs) all through college. This testable prediction is an example of a:
a. theory.
b. hypothesis.
c. confirmation.
d. principle.
Answers
Answer:
b. hypothesis.
Step-by-step explanation:
many cities, researchers have found a strong positive linear relationship between ice cream sales and the crime rate.
Answers
While researchers may have found a strong positive linear relationship between ice cream sales and the crime rate in many cities, it does not necessarily mean that one directly causes the other.
There could be other underlying factors or variables at play that are influencing both ice cream sales and the crime rate. For example, both variables might be influenced by external factors such as weather conditions, population density, or economic factors.
Additionally, it's possible that the observed relationship is coincidental or driven by statistical outliers. Without further evidence and a comprehensive analysis, it is not appropriate to conclude a direct causal relationship between ice cream sales and the crime rate based solely on a positive correlation.
To establish a causal relationship, further research would be needed to identify the specific mechanisms or factors that link ice cream sales to the crime rate in order to determine if there is a direct cause-and-effect relationship between the two variables.
Learn more about economic here:
https://brainly.com/question/30187093
#SPJ11
many cities, researchers have found a strong positive linear relationship between ice cream sales and the crime rate. Explain.
4. How many 5 -digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Answers
There are 336 different 5-digit telephone numbers that can be constructed using the digits 0 to 9, starting with "67" and with no repeated digits.
To answer your question, we need to find the number of ways to arrange the remaining three digits after "67" is fixed.
Since we cannot repeat any digit, the first digit has 8 possibilities (0 to 9 except for 6 and 7).
the second digit has 7 possibilities, and the third digit has 6 possibilities.
To find the total number of arrangements, we multiply the number of possibilities for each digit together:
8 × 7 × 6 = 336.
Therefore, there are 336 different 5-digit telephone numbers that can be constructed using the digits 0 to 9, starting with "67" and with no repeated digits.
To know more about numbers visit :
https://brainly.com/question/32585587
#SPJ11
For each annual rate of change, find the corresponding growth or decay factor. +70 %
Answers
The corresponding growth factor of +70% is 1.7
The formula for the annual rate of change is
1 ± r (1)
where r = rate of change
and ± sign depends upon whether it is a growth or decay factor. If it is growth factor then it is plus sign otherwise negative sign.
According to the question we have been given the growth that is +70%. Since there is plus sign therefore it is a growth factor.
Thus, r = + 0.7
Putting this value in equation (1) we get
= 1 + 0.7
= 1.7
Hence the corresponding growth factor of +70% is 1.7
Learn more about growth factor here : https://brainly.com/question/27161222
#SPJ4
Number 11 please write the equation for the standard function use transformations and critical points of the graph

Answers
Solution
- The formula for the vertex form of a quadratic equation is given below:
\(\begin{gathered} y=a(x-h)^2+k \\ where, \\ (h,k)\text{ is the coordinate of the vertex} \end{gathered}\)- The vertex of the quadratic equation is depicted below:
- Thus, the vertex of the quadratic graph is V(2, -2).
- The equation of the graph becomes:
\(y=a(x-2)-2\)- To find the value of "a", we apply the coordinate given (-1, 6). This is done below:
\(\begin{gathered} when\text{ }x=-1,y=6 \\ \\ 6=a(-1-2)^2-2 \\ 6=a(-3)^2-2 \\ 6=9a-2 \\ \text{ Add 2 to both sides} \\ 9a=8 \\ \text{ Divide both sides by -3} \\ \\ a=\frac{8}{9} \end{gathered}\)Final answer
The equation is:
\(y=\frac{8}{9}(x-2)^2-2\)
Apply the distributive property to create an equivalent expression.
( 1 -2g +4h)\cdot 5 =(1−2g+4h)⋅5
Answers
Given:
The expression is
\((1-2g+4h)\cdot 5\)
To find:
The equivalent expression.
Solution:
Distributive property of multiplication over addition is
\(a(b+c)=ab+ac\)
Where, a, b and c are real numbers.
We have,
\((1-2g+4h)\cdot 5\)
Using distributive property, we get
\(=(1)\cdot 5+(-2g)\cdot 5+(4h)\cdot 5\)
\(=5-10g+20h\)
Therefore, the expression \(5-10g+20h\) is equivalent to the given expression.
Answer:
5-10g+20h
Step-by-step
Please give Brainliest :)
Suppose that f(x) = x² + an−1x²−1¹ + ... + a。 € Z[x]. If r is rational and x — r divides f(x), prove that r is an integer.
Answers
To prove that if a rational number r divides the polynomial f(x) = x² + aₙ₋₁xⁿ⁻¹ + ... + a₀ ∈ ℤ[x], then r must be an integer, we can utilize the Rational Root Theorem.
According to the Rational Root Theorem, if a rational number r = p/q, where p and q are coprime integers and q ≠ 0, divides a polynomial with integer coefficients, then p must divide the constant term a₀, and q must divide the leading coefficient aₙ.
Let's assume r = p/q divides f(x), which means that f(r) = 0. Substituting r into f(x), we obtain 0 = r² + aₙ₋₁rⁿ⁻¹ + ... + a₀. Since all coefficients and r are rational numbers, we can multiply the entire equation by qⁿ to eliminate the denominators. This yields 0 = (pr)² + aₙ₋₁(pr)ⁿ⁻¹ + ... + a₀qⁿ.
Since q divides the leading coefficient aₙ, it follows that q divides each term of aₙ₋₁(pr)ⁿ⁻¹ + ... + a₀qⁿ, except for the first term, (pr)². As q divides the entire equation, including (pr)², q must also divide (pr)². Since p and q are coprime, q cannot divide p. Therefore, q must divide (pr)² only if q divides r².
Since q divides r² and r is rational, q must also divide r. But p and q are coprime, so q dividing r implies that q divides p. Thus, r = p/q is an integer.
Therefore, if a rational number r divides the polynomial f(x) with integer coefficients, r must be an integer.
To know more about polynomials, refer here :
https://brainly.com/question/12491437#
#SPJ11
what is the largest even integer which cannot be written as the sum of two odd composite numbers? (recall that a positive integer is said to be composite if it is divisible by at least one positive integer other than 1 and itself.)
Answers
Largest even integer which cannot be written as the sum of two odd composite numbers is 38 if it is divisible by at least one positive integer other than 1 and itself.
The positive even integers which cannot be expressed as the sum of 2 composite odd numbers are: 2,4,6,8,10,12,14,16,20,22,26,28,32,38. This sequence is A118081.
All we have to do now is check the even numbers smaller than 44
. The largest, 42 is a multiple of 3 so it’s handled as 42=9+33 and the next one down, 40 is handled as 40=25+15.But the next one down is our culprit: 38 is not the sum of two odd composite numbers, as you can readily check.
First, what are these “odd composite numbers” anyway? The number 1is considered neither prime nor composite (it’s a unit), so it’s out. 3,5 and 7 are prime. The smallest odd composite number is, therefore, 9 and the next one is 15 .So we have 18=9+9 24=9+1 and 30=15+15 as some even numbers which can be written as a sum of two odd composites, but so far it doesn’t look promising: plenty of even numbers, like 10 or 20 or 32 cannot be so written.
Learn more about integer here:-
brainly.com/question/9097648
#SPJ4
Find the sum of the next numbers in the
sequence below.
8, 9, 12, 18, 28,__,__
Answers
Answer:
the two next numbers are 43 and 64 , sum = 107
Step-by-step explanation:
see attachment
so the next two nos. of the sequence would be 43 and 64
And we are done!
-Rishabh

pls help ill give brainliest lolz

Answers
Answer:
t =5
Step-by-step explanation:
-7(2-t)=21
-14+7t=21
7t=35
t=5
Given: Triangle ADE~
Triangle CBF, ED bisects Angle ADC and F B bisects Angle ABC.
Prove: DF BE is a parallelogram.
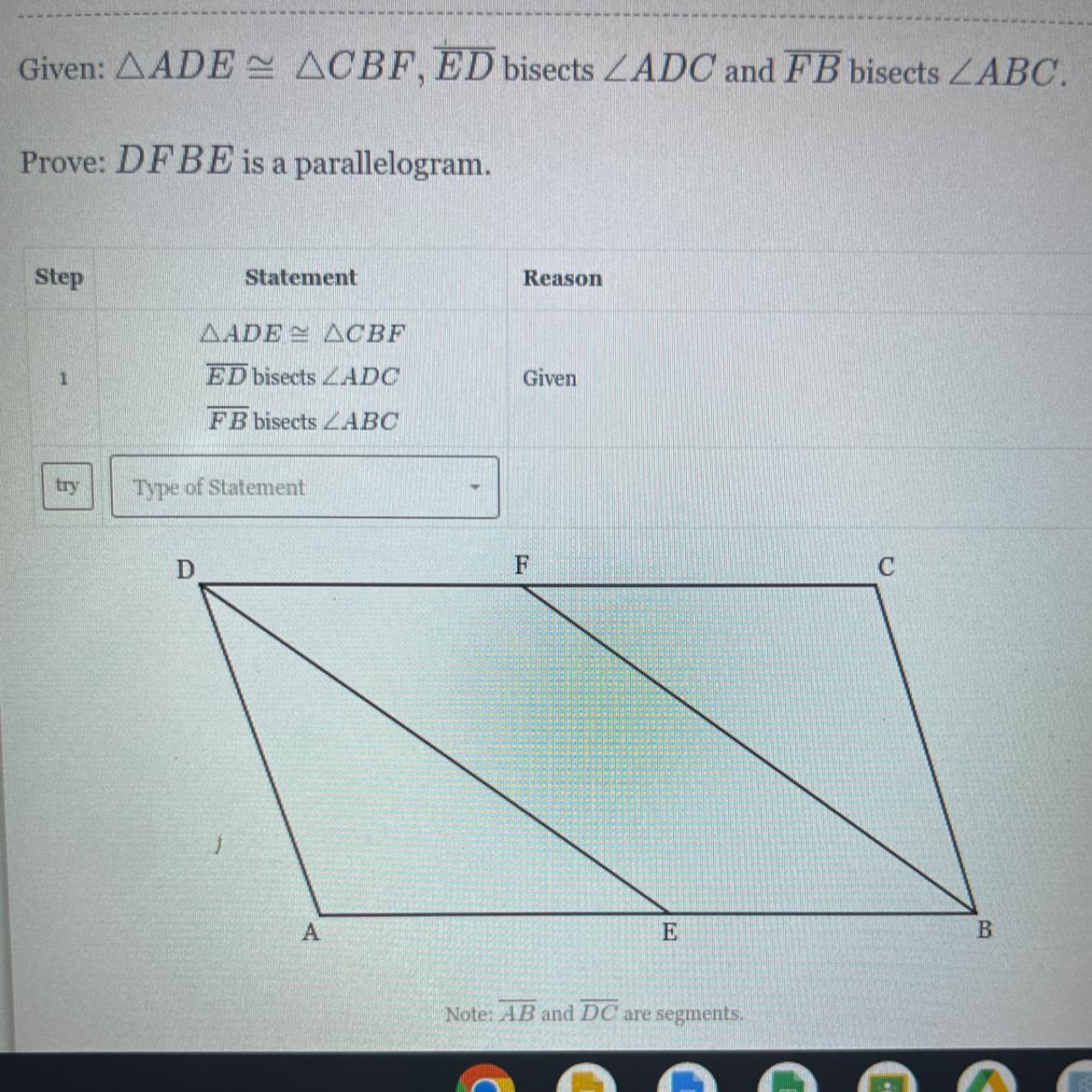
Answers
Answer:
See proof below
Step-by-step explanation:
Given \(\triangle ADE \cong \triangle CBD\)
Then, \(\angle AED \cong \angle CFB\) because corresponding parts of congruent triangles are congruent.
Since \(\angle AED \text{ and } \angle DEB \text{ form a linear pair}\), by the linear pair postulate, \(\angle AED \text{ and } \angle DEB \text{ are supplementary}\).
Similarly, \(\angle CFB \text{ and } \angle BFD \text{ form a linear pair}\), so by the linear pair postulate, \(\angle CFB \text{ and } \angle BFD \text{ are supplementary}\).
By the Congruent supplements theorem, since \(\angle AED \text{ and } \angle DEB \text{ are supplementary}\), \(\angle CFB \text{ and } \angle BFD \text{ are supplementary}\), and \(\angle AED \cong \angle CFB\) , then \(\angle DEB \cong \angle BFD\). (note, this is one pair of opposite angles inside quadrilateral DFBE)
Recalling that \(\overline {ED} \text{ bisects } \angle ADC, \text{ and } \overline {FB} \text{ bisects } \angle ABC\), then, \(\angle ADE \cong \angle CDE\), and \(\angle CBF \cong \angle FBA\) by definition of angle bisector.
Note that \(\angle ADE \cong \angle CBF\) because corresponding parts of congruent triangles are congruent.
Also, note that \(\angle EDF \cong \angle EDC\) and \(\angle FBA \cong \angle FBE\) because B, E, A are colinear, and D, F, C are colinear.
So, by the transitive property of angle congruence, \(\angle EDF \cong \angle FBE\) (This is the other pair of opposite angles inside quadrilateral DFBE)
So, since both pairs of opposite angles are congruent, quadrilateral DFBE is a parallelogram, by a theorem about quadrilateral properties (your book may or may not have a name for it. It may just have a number).
if the sum of 2 digits no. is 9 and their differenc is 1 find te no.
Answers
Answer:
Let the ten's digit no. be x and one's digit no. be y.
So the no. will be = 10x+y.
Given : x+y=9-----(I)
9(10x+y)=2(10y+x) ⇒88x−11y=0 -----(II)
On solving I and II simultaneously you will get x=1 and y=8.
Therefore your desired no. is 18.
Step-by-step explanation:
Hope it is helpful.....
The width of a rectangle is 6t-1.5 feet and the length is 1.5t+6 feet. Find the perimeter of the rectangle. The perimeter of the rectangle is nothing feet.
Answers
Answer:
15t+9 ft
Step-by-step explanation:
Given data
Width= 6t-1.5 ft
Length= 1.5t+6 ft
Required
The perimeter
The expression for perimeter is
P= 2L+2W
P= 2(1.5t+6)+ 2(6t-1.5)
open bracket
P= 3t+12+ 12t-3
collect like terms
P= 3t+12t+12-3
P= 15t+9 ft
Hence the perimeter is 15t+9 ft
I'm really confused with this plz help

Answers
Answer:
4 terms
constant 10
third term is -7z
coefficient of the second term is 3
Step-by-step explanation:
-5x+3y -7z +10
There are 4 terms, -5x, 3y ,-7x, 10
The constant is the term without the variable ( letter)
The constant is 10
The third term is -7z
The coefficient is the number in front of the variable
The coefficient of the second term 3y is 3
For part a, we are asked how many terms does this expression have.
Well a term can be a number, a variable, or it can
even be a number times one or more variables.
So the terms would be -5x, +3y, -7z, and +10.
For part b, we are asked what is the constant.
Usually, constants are numbers all by themselves.
So here, the constant would be 10.
In part c, we are asked what is the third term.
Well, looking at the expression, we can see that -7z is the third term.
Finally, what is the coefficient of the second term.
The coefficient is the number before your variable.
So here, the coefficient would be 3.