Answers
Answer:
A) -0.6
B) 0.5
Step-by-step explanation:
slope=(2--1)÷(9-3)
Related Questions
Events D and E are independent, with P(D)- 0.6 and P(D and E) - 0.18. Which of the following is true? A. P(E)- 0.12 B. P(E) = 0.4 C. P(D or E)-0.28 D. P(D or E) 0.72 E. P(D or E)-0.9
Answers
The correct statement is: A. P(E) = 0.3. The probability of event E, denoted as P(E), is equal to 0.3.
To determine the correct answer, let's analyze the given information.
We know that events D and E are independent, which means that the occurrence of one event does not affect the probability of the other event happening.
Given:
P(D) = 0.6
P(D and E) = 0.18
Since events D and E are independent, the probability of both events occurring (P(D and E)) can be calculated as the product of their individual probabilities:
P(D and E) = P(D) * P(E)
Substituting the given values:
0.18 = 0.6 * P(E)
To find the value of P(E), we can rearrange the equation:
P(E) = 0.18 / 0.6
P(E) = 0.3
Therefore, the correct answer is A. P(E) = 0.3.
Learn more about probability here: https://brainly.com/question/32117953
#SPJ11
Help Ur boy out here having some problem

Answers
Answer:
The answer is option:
C. 10% of her customers ordered an appetizer and dessert.
Diff of squares help me out
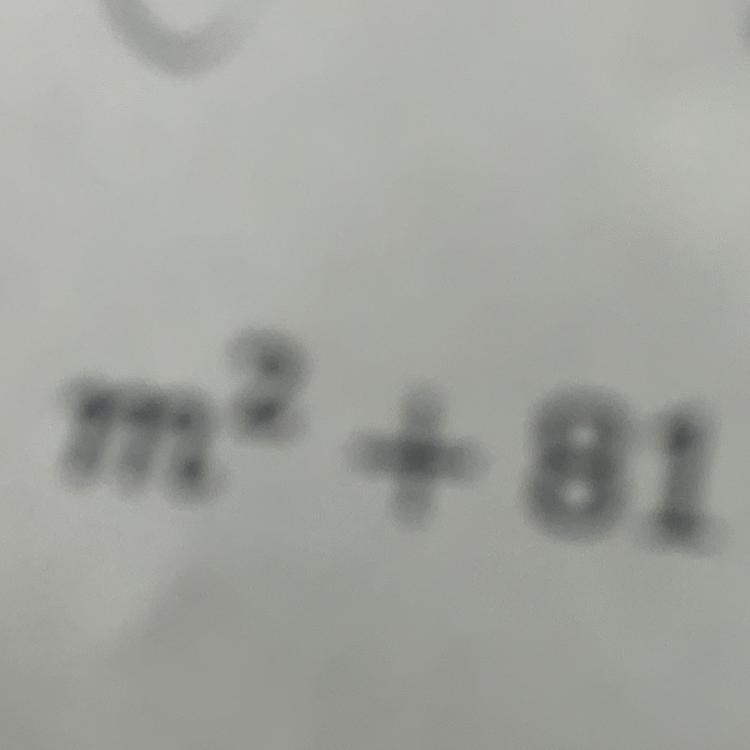
Answers
Answer:
9
Step-by-step explanation:
9 is the correct answer
what is the next term in the number pattern? 77, 64, 53, 44, 37
Answers
Answer:
32
...when you subtract five from 37
It is a pattern that goes:
-13
-11
-9
-7
and now -5 = 32
Four fifths of the third grade went on a trip to the zoo. If 64 children made the trip, how many children are in the third grade
Answers
Therefore , the solution of the given problem of linear equation comes out to be S = 80 third-grade kids.
A linear equation is precisely what?A straightforward regression curve is created using the equation y=mx+b. The y-intercept is m, and the slope is B. The previous sentence is usually referred regarded as a "mathematical formula integrating multiple variables," even though y or y are different parts. Only two variables are present in bivariate linear equations. There are no known solutions to application issues involving linear equations.
Here,
The ability to convert words and phrases into clear, succinct math equations is essential for solving word (story) issues (variables and operations).
Let S represent the total number of third-graders.
The phrase "four fifths of a third grade" denotes 4/5 * S. ("of" usually means multiply)
"How many kids are in the third grade?" means to report S. "If 64 pupils made the trip" denotes that 4/5 * S = 64
, the math is as follows: (4/5)*S = 64 (multiply both sides by 5/4
S = 80 third-grade kids.
Therefore , the solution of the given problem of linear equation comes out to be S = 80 third-grade kids.
To know more about linear equation visit:
https://brainly.com/question/11897796
#SPJ1
The complete question is "Four fifths of the third grade went on a trip to the zoo. If 64 children made the trip, how many children are in the third grade?"
Due in 11 minutes please help me ASAP

Answers
Answer: (d)
Step-by-step explanation:
Given
No of tickets sold can be given by the equation
\(35x-260>1000\)
Solving inequality
adding 260 on both sides
\(35x-260+260>1000+260\\35x>1260\)
Now, divide the inequality by 35
\(x>\frac{1260}{35}\\x>36\)
Thus artist need to sell a minimum of 37 tickets to earn more than $1000
what is the value of this expression below when w=10 and x=7
10w-7x
Answers
Answer:
=51
Step-by-step explanation:
10w - 7x
10(10) - 7(7)
100 - 49
=51
7*7=49
Then subtract:
100-49=51
So the answer is 51
The amunt of money that college students spend on rent each month is usually between $300 and $600. However, there are a few students who spend $1,300. What measure of spread would be most appropriate to measure the amount of money that college student spend on rent per month? Explain in detail why or why not one of the below measures would be used.
A. Median
B. Range
C. Standard Deviation
D. Inquartile Range
Answers
The range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
To measure the amount of money college students spend on rent per month, the most appropriate measure of spread would be the range. The range is the simplest measure of spread and is calculated by subtracting the lowest value from the highest value in a data set. In this case, the range would be $1,300 - $300 = $1,000.
The median would not be the best choice in this scenario because it only represents the middle value in a data set. It does not take into account extreme values like the $1,300 rent expense.
Standard deviation would not be the most appropriate measure of spread in this case because it calculates the average deviation of each data point from the mean. However, it may not accurately represent the spread when extreme values like the $1,300 rent expense are present.
The interquartile range (IQR) would not be the best choice either because it measures the spread of the middle 50% of the data set. It does not consider extreme values and would not accurately represent the range of rent expenses in this scenario.
In summary, the range would be the most appropriate measure of spread in this case because it takes into account the extreme values of $300 and $1,300 and provides a clear measure of the difference between them.
Know more about Standard deviation here,
https://brainly.com/question/29115611
#SPJ11
Oscar saves 40% of his monthly check for college. He earned $450 last month. How much money did Oscar save for college?
Answers
Answer
It is $180
Step-by-step explanation:
You do 450 times 40% and you get $180
Find the value of p for which the graph of f has exactly one point with a gradient of zero.

Answers
The value p = 1/2 + √(3)/2 does give us exactly one point with a gradient of zero.
What is quadratic equation?A quadratic equation, or sometimes just quadratics, is a polynomial equation with a maximum degree of two. It takes the following form:
ax² + bx + c = 0
To find the value of p for which the graph of f has exactly one point with a gradient of zero, we need to find the derivative of f(x) and set it equal to zero.
First, we can simplify f(x) by factoring out 4x:
f(x) = 4x(x + p/(4x+4))
Now, we can find the derivative of f(x):
f'(x) = 4(x + p/(4x+4)) + 4x(1 - p/(4x+4)²)
To find the point(s) where f'(x) = 0, we set it equal to zero and solve for x:
4(x + p/(4x+4)) + 4x(1 - p/(4x+4)²) = 0
Simplifying and multiplying through by (4x+4)²:
16x³ + 32px² + 16px - 16p = 0
Dividing through by 16x:
x² + 2px + p - 1 = 0
Now, we can use the discriminant of this quadratic equation to determine the value of p that gives exactly one point with a gradient of zero. The discriminant is:
b² - 4ac = (2p)² - 4(1)(p-1) = 4p² - 4p + 4 = 4(p² - p + 1)
For the graph of f to have exactly one point with a gradient of zero, the discriminant must be equal to zero, because that means there is only one value of x that satisfies f'(x) = 0. So, we set the discriminant equal to zero and solve for p:
4(p² - p + 1) = 0
p² - p + 1 = 0
Using the quadratic formula:
p = (1 ± √(1 - 4))/2 = 1/2 ± √(3)/2
So, the two possible values of p for which the graph of f has exactly one point with a gradient of zero are:
p = 1/2 + √3)/2
p = 1/2 - √(3)/2
Note that we should check that these values of p actually give us a point with a gradient of zero. If we substitute each value of p back into the derivative f'(x), we get:
When p = 1/2 + √(3)/2:
f'(x) = 4(x + (1/2 + √(3)/2)/(4x+4)) + 4x(1 - (1/2 + √(3)/2)/(4x+4)²)
Simplifying, we get:
f'(x) = (16x³ - 8x² + (4√(3) - 4)x + 4√(3) - 4)/(4(x+1)²(x+1+√(3)))
We can see that the denominator is always positive, so the gradient of f can only be zero when the numerator is zero. To find the value of x that satisfies this, we need to solve the cubic equation:
16x³ - 8x² + (4√(3) - 4)x + 4√(3) - 4 = 0
Using numerical methods, we find that there is only one real root, which is approximately x = 0.265. Therefore, the value p = 1/2 + √(3)/2 does give us exactly one point with a gradient of zero.
Learn more about quadratic equation on:
https://brainly.com/question/1214333
#SPJ1
If a function is differentiable then it is continuous.
Answers
The statement "If a function is differentiable, then it is continuous" is generally true. In summary, if a function is differentiable at a point, it must also be continuous at that point.
Differentiability is a stronger condition than continuity. If a function is differentiable at a point, it means that it has a derivative at that point, indicating the existence of a well-defined tangent line.
A key property of differentiability is that it implies continuity. In other words, if a function is differentiable at a point, it must also be continuous at that point.
On the other hand, a function can be continuous without being differentiable. Continuous functions have no abrupt jumps, holes, or vertical asymptotes in their graphs. However, they may have corners, cusps, or vertical tangents, which prevent them from being differentiable at those points. Therefore, while differentiability guarantees continuity, continuity does not necessarily imply differentiability.
Learn more about continuous function here: brainly.com/question/28228313
#SPJ11
Complete question - Write the conserve and contrapositive of the following statement- "If a function is differentiable then it is continuous."
Factor this equation 144x2-49
Answers
We have the following equation
\(144x^2-49\)We must factor this, in this case with the fourth case factorization.
The solution is the following:
\((12x+7)(12x-7)\)If Dylan buys a book that is 25% off, what percent of the original price does Dylan pay?
Answers
Answer:
75 percent is your answer
Can you tell me how to solve for X

Answers
Answer:
answer is D)10
Step-by-step explanation:
there's a square in the corner, and that tells you this angle is a right angle which is 90degrees
so 90-60=3x
30=3x
x=10
Answer:
A. 30
x=30
Step-by-step explanation:
That is a 90 degree angle. 90-60=30
The table of values forms a quadratic function f(x).
x f(x)
−3 48
−2 50
−1 48
0 42
1 32
2 18
3 0
What is the equation that represents f(x)?
Answers
The equation of the quadratic function represented by the table is;
f(x) = -2x² - 8x + 42
How to find the quadratic equation from a table?The general form of a quadratic equation is;
y = ax² + bx + c
At x = 0, y = 42
Thus, c = 42
When x = 3, y = 0.
Thus;
9a + 3b + 42 = 0
9a + 3b = -42 -----(1)
At x = 1, y = 32. Thus;
a + b + 42 = 32
a = -10 - b
Put -10 - b for a in eq 1 to get;
9(-10 - b) + 3b = -42
-90 - 6b = -42
-6b = 48
b = -8
a = -10 - (-8)
a = -2
Thus;
f(x) = -2x² - 8x + 42
Read more about Quadratic Equation at; https://brainly.com/question/1214333
#SPJ1
Round your answers to the nearest tenth.
45°
C
(o) a = 0
(b) d= 4
3
45°
X
60°
/30°
5
8

Answers
The measure of side length a and side length d in the right triangles are 3√2 and \(\frac{8\sqrt{3} }{3}\) respectively.
What is the measure of the side lengths a and d?The figures in the image are a right triangle.
For right triangle 1)
Angle θ = 45 degrees
Opposite to angle θ = 3
Hypotenuse = a
To solve for side length a, we use the trigonometric ratio.
Note that: sine = opposite / hypotenuse
sinθ = opposite / hypotenuse
Plug in the values:
sin( 45 ) = 3 / a
Solve for a
a = 3 / sin( 45 )
a = 3√2
Right triangle 2)
Angle θ = 30 degrees
Adjacent to angle θ = 8
Opposite to angle θ = d
To solve for side length d, we use the trigonometric ratio.
Note that: tan = opposite / adjacent
tan θ = opposite / adjacent
Plug in the values:
tan( 30 ) = d / 8
d = tan( 30 ) × 8
d = \(\frac{8\sqrt{3} }{3}\)
Therefore, the measure of side d is \(\frac{8\sqrt{3} }{3}\).
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
what is the minus 60 plus 40 =x plus y= x+9
Answers
60+40=x
y=x+9
MInus
x=100
y=109
Diffrence 9
Answer:
x = -20
y = -11
Data from the past three months at Gizzard Wizard (GW) shows the following: Month Prod. Volume DM DL MOH May 1000 $400.00 $600.00 $1200.00 June 400 160.00 240.00 480.00 July 1600 640.00 960.00 1920.00 If GW uses DM$ to apply overhead, what is the application rate?
Answers
The application rate is 3 (per DM$).
The given below table shows the monthly production volume, direct materials, direct labor, and manufacturing overheads for the past three months at Gizzard Wizard (GW):
Month Prod. Volume DM ($)DL ($)MOH ($)May 1000$400.00$600.00$1200.00
June 400160.00240.00480.00
July 1600640.00960.001920.00
By using DM$ to apply overhead, we have to find the application rate. We know that the total amount of manufacturing overheads is calculated by adding the cost of indirect materials, indirect labor, and other manufacturing costs to the direct costs. The formula for calculating the application rate is as follows:
Application rate (per DM$) = Total MOH cost / Total DM$ cost
Let's calculate the total cost of DM$ and MOH:$ Total DM$ cost = $400.00 + $160.00 + $640.00 = $1200.00$
Total MOH cost = $1200.00 + $480.00 + $1920.00 = $3600.00
Now, let's calculate the application rate:Application rate (per DM$) = Total MOH cost / Total DM$ cost= $3600.00 / $1200.00= 3
Therefore, the application rate is 3 (per DM$).
Hence, the required answer is "The application rate for GW is 3 (per DM$)."
Know more about application rate here,
https://brainly.com/question/24266380
#SPJ11
. Explain the Error: Katie said, “All Negative numbers are integers.” What was her error?
Answers
Answer:
All Negative numbers are NOT integers
Step-by-step explanation:
For example, If we take the negative number, -5/6
It is NOT a integer, it is a rational number.
Thus, this statement is wrong.
Answer:
It should be all whole negative number are integers
Step-by-step explanation:
Because integers are whole numbers
not included the fraction
ILL GIVE BRAINALIST IF YOU ANSWER CORRECTLY
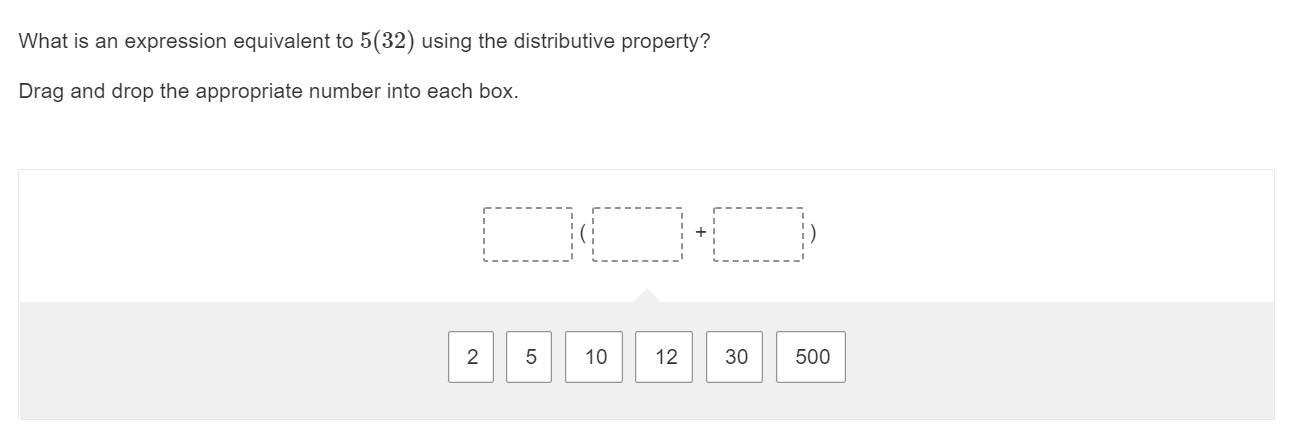
Answers
The Expression3(x-9) equivalent to
Answers
Answer:
3x - 27
Step-by-step explanation:
3(x-9)
Distribute
3x * -3*9
3x - 27
Answer:
Brainliest!
Step-by-step explanation:
it is equivialent to 3x-27
just simplify the equatoin
Gasoline prices for the first six months of 2004 are shown in the table below. Using a logarithmic model, what is the best
prediction for gas prices in the ninth month of 2004?
Answers
Answer:
A) $2.10
Step-by-step explanation:
I got it right on edge
Answer:
A $2.10
Step-by-step explanation:
edgw 2020
can someone please give me the awnsers !!!!!!

Answers
I'll do the left side.
1:
\(-6=\frac{n}{3} -8 \\2 = \frac{n}{3} \\n = 6\)
Inverses are your friends, for example to get \(n - 3 = 0\) where n is on one side, do the inverse of subtraction ( addition) so you get \(n - 3 + 3 = 3 \\\\n = 3\)
\(-7 = \frac{n}{4} - 3 \\-4 = \frac{n}{4}\\n = -16\)
\(-13 = 5y + 7 \\-6 = 5y \\\)
On "y" there is a coefficient of 5, aka \(5*y\), the inverse of multiplication is division
\(\frac{-6}{5} = y\)
\(-6 + \frac{x}{2} = -3\\ \frac{x}{2} = 3 \\x = 6\)
You finish the rest, but you gotta remember this, isolate the variable (x, y, z, whatever) by doing inverses
inverses
addition - subtraction
multiplication - division
Everything in math builds on this!!!
Solve the equation using square roots. Select the solution(s)

Answers
Answer:
problem is x^2 +6=0
Step-by-step explanation:
Answer:
no real solutions
Step-by-step explanation:
Given
x² + 6 = 0 ( subtract 6 from both sides )
x² = - 6 ( take the square root of both sides )
x = ± \(\sqrt{-6}\)
\(\sqrt{-6}\) has no real solutions
There were 1125 books sold last week at Sid's Bookstore. The circle graph below summarizes these books by genre.
The central angle for the Self-Help slice is 80.64. How many of the books sold were Self-Help books?

Answers
Answer:
Number of self-Help books sold = 252 books
Step-by-step explanation:
Total books sold last week = 1,125
Central angle for the Self-Help slice = 80.64°
Total angle in a circle = 360°
How many of the books sold were Self-Help books?
Number of self-Help books sold =
Central angle for the Self-Help slice / Total angle in a circle × total number of books sold
= 80.64° / 360° × 1,125
= 0.224 × 1,125
= 252
Number of self-Help books sold = 252 books
which subshell (for example, 1s) is designated by each set of quantum numbers below?
Answers
The subshell designated by each set of quantum numbers is as follows:
a) n=3, l=1 -> 3p subshell
b) n=4, l=2 -> 4d subshell
c) n=2, l=0 -> 2s subshell
d) n=5, l=3 -> 5f subshell
In the electron configuration of an atom, each electron is described by a set of four quantum numbers, which includes the principal quantum number (n), the angular momentum quantum number (l), the magnetic quantum number (m), and the spin quantum number (s). The second quantum number (l) determines the shape of the subshell, which in turn influences the energy level and chemical behavior of the atom. The letter designation for each subshell is based on the value of the angular momentum quantum number (l): s (l=0), p (l=1), d (l=2), f (l=3), and so on. Therefore, for a given set of quantum numbers, we can determine the subshell designation by identifying the value of l.
Learn more about Quantum Numbers here: brainly.com/question/14288557
#SPJ11
Which table of ordered pairs represents a proportional relationship?
X
0
5
10
X246
123
2
3
134
3
4
10
20
30
10
20
30
234
4
10
13

Answers
Answer:
The second option
Step-by-step explanation:
The second option is a proportional relationship since the ratio between y and x is constant.
10/2 = 5
20/4 = 5
30 / 6 = 5
A bag contains 40 marbles. The probability of selecting a red marble at random is 1/5. How many red marbles are in the bag?
Answers
Answer:
8 red marbles.
Step-by-step explanation:
All together we have 40 marbles. The fraction of marbles that are red is 1/5 which means that we should divide the total number of marbles, which is 40 by the denominator ( Bottom number of fraction ) 5 so that we get the number of groups that have 1 red marble in them. In this case we have 8 groups.
40/5=8
You always divide by the denominator ( Bottom number of fraction ) first and then you multiply your answer by the numerator ( Top number of fraction ) .
If each group has 1 red marble in it and we have 8 groups, it means that we have 8 red marbles in the bag.
1 * 8 = 8 red marbles in the bag
If the numerator (number above the fraction line) was more than one, then this would mean that we have more than 1 marble in each group of marbles.
Example:
If we had 3/5 we would have 3 marbles in each group of marbles. This means that instead of doing 1 * 8 we would have to do 3 * 8 = 24. We would have 24 red marbles in the bag.
Easy and quick way if you do not need the explanation:
Another way we could do this is by simply multiplying the fraction ( 1/5 ) by the total number of marbles ( 40 ). This would still give us an answer of 8 red marbles in the bag. 40/5=8, 8*1=8
The world death rate in 1960 was 17. 7 deaths per 1000 people. If there were 3. 032 billion people in the world in 1960, how many deaths were there?
Answers
There were 53666.4 deaths in 1960. The solution has been obtained by using arithmetic operations.
What are arithmetic operations?
Mathematicians claim that the four fundamental operations, also referred to as "arithmetic operations," can characterise all real numbers. The four mathematical operations of division, multiplication, addition, and subtraction produce the terms quotient, product, sum, and difference, respectively.
We are given that the world death rate in 1960 was 17. 7 deaths per 1000 people.
There were 3.032 billion people in the world in 1960 which means that there were 3032 thousand people.
So, the total deaths in 1960 were
⇒3032 * 17.7
⇒53666.4
Hence, there were 53666.4 deaths in 1960.
Learn more about arithmetic operations from the given link
https://brainly.com/question/30283549
#SPJ1
N is the centriod of triangle. Find XN if XG = 33

Answers
Answer:
22
Step-by-step explanation:
The centroid divides a median in two parts that have this ratio = 1/3 and 2/3
In particular the part between the vertex and the centroid is 2/3 of the median.
So we have:
XN = (33 * 2)/3 = 22
