PLEASE HELP WITH ALGEBRA 1
Complete the square.
4t²-16t+12
Answers
The equivalent expression is (t - 2)² - 1
How to complete the square.From the question, we have the following parameters that can be used in our computation:
4t²-16t+12
Divide through the equation by 4
So, we have the following representation
t² - 4t + 3
Take the coefficient of t
k = -4
Divide by 2
k/2 = -2
Square it
(k/2)^2 = 4
So, we have
t² - 4t + 3 + 4 - 4
Rewrite as
t² - 4t + 4 + 3 - 4
Express as squares
(t - 2)² - 1
Hence, the expression is (t - 2)² - 1
Read more about complete the square at
https://brainly.com/question/8665569
#SPJ1
Related Questions
Given \(\displaystyle W(t)=\int^t_2\ln(x-1)dx\), find \(\displaystyle W''\left(\frac{5}{2}\right)\).
Answers
The value of W''(5/2) is 2/3.
Given: W(t) = ∫ ln(x - 1) dx, where the limits of integration are from 2 to t.
To find the first derivative, we can apply the Fundamental Theorem of Calculus:
W'(t) = d/dt [∫ ln(x - 1) dx]
By the chain rule, we have:
W'(t) = ln(t - 1) * d/dt(t) - ln(2 - 1) * d/dt(2)
Since d/dt(t) = 1 and d/dt(2) = 0, the equation simplifies to:
W'(t) = ln(t - 1)
Now, to find the second derivative, we differentiate W'(t) with respect to t:
W''(t) = d/dt [ln(t - 1)]
By the chain rule, we have:
W''(t) = 1/(t - 1) * d/dt(t - 1)
Since d/dt(t - 1) = 1, the equation simplifies to:
W''(t) = 1/(t - 1)
Now, we can evaluate W''(5/2) by substituting t = 5/2 into the equation:
W''(5/2) = 1/((5/2) - 1)
W''(5/2) = 1/(5/2 - 2/2)
W''(5/2) = 1/(3/2)
W''(5/2) = 2/3
Therefore, W''(5/2) = 2/3.
Learn more about Differentiation here:
https://brainly.com/question/24062595
#SPJ1
sin² x + cos²x = 1
Which Trigonometric Identity is given above?
- Pythagorean Identity
- Lagrange's Trigonometric Identity
- Angle Sum and Difference Identity
- Tangent Identity
Answers
The Trigonometric Identity sin² x + cos²x = 1 is: A. Pythagorean Identity.
What is Pythagorean Identity?The Pythagorean Identity which tend to asserts that for every angle x, the sum of the squares of the sine and cosine of x is equal to one is known as or called a trigonometric identity.
The Pythagorean identity can be expressed as:
sin² x + cos² x = 1
This identity is crucial to understanding trigonometry and tend to have several uses in numerous branches of science and engineering.
Therefore the correct option is A.
Learn more about Pythagorean Identity here:https://brainly.com/question/24287773
#SPJ1
can someone plz help me with this question asap: solve the equation for x in the terms of c. 2/3(cx + 1/2) - 1/4 = 5/2
A: x = 9/4c
B: x = 27/8c
C: x = 29/8c
D: x = 29/18c
Answers
For all parts of this question, use the function 4x + 3y = 9
Part A: compeleré the x-y table. (Photo provided)
Part B: evaluate f(6)
Part C: what is the y-intercept of the equation?

Answers
The x-y table is completed as follows:
1) y = 11 where x = -6
y = 7 where x = -3
y = 3 where x = 0
y = -1 where x = 3
2) f(6) results in y = -5
3) the intercept of the equation 4x + 3y = 9 are (0,3). See the attached graph.
What is the rationale for the above response?To derive the y values given in (1) above, all that we need to do is plug in th value of x into the equation and solve. Here is an example:
Given 4x + 3y = 9, the value of y when x = -6 is:
4(-6) + 3y = 9
⇒ -24 + 3y = 9
Collect like terms over the equals sign and we have:
3y = 9+ 24
3y = 33 (divide both sides by 3)
3y/3 = 33/3
y = 11
The above steps can be repeated for all other cases of x to get y.
2) f(6) simply means to find y when x is set to 6. The steps above apply.
f(x) = 4x + 3y - 9
-3y = 4(6) -9
-3y = 24-9
-3y = 15 (divide both sides by -3)
-3y/-3 = 15/15
y = -5
3) Note that when a point crosses the y-axis, it is referred to as the y-intercept. The intercept of a line is the point at which it intersects the x-axis or the y-axis. If no axis is supplied, the y-axis is normally used. The letter 'b' is commonly used to represent it.
Learn more about intercept;
https://brainly.com/question/29113022
#SPJ1

Pls help me out with this will mark brainliest
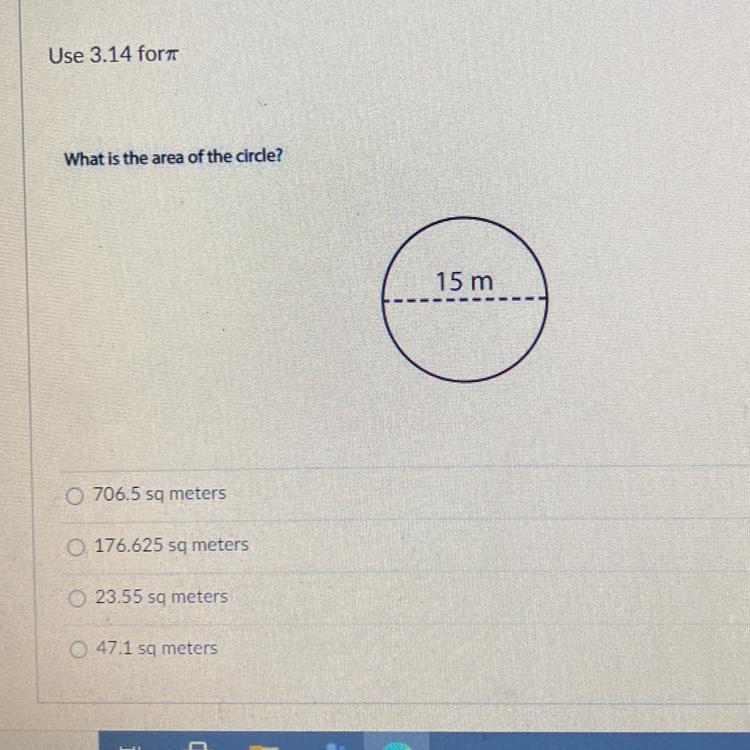
Answers
at a certain high school, the prom committee is going to choose new members. there are students from the junior class and students from the senior class who are willing to be new members. in how many ways can new members be chosen if more than must be from the senior class?
Answers
Answer:
Step-by-step explanation:
7 students from the Junior class.
6 students from the Senior class.
4 new members are to be chosen.
Required: Find the number of ways 4 new members can be chosen if 2 or fewer must be from the senior class. So, Therefore, the correct answer is 560 ways.
integer c is 2/3 of the way from A on the integer line. Determine C
A=-23
B=-5
Answers
Answer:
Please see picture below
Step-by-step explanation:
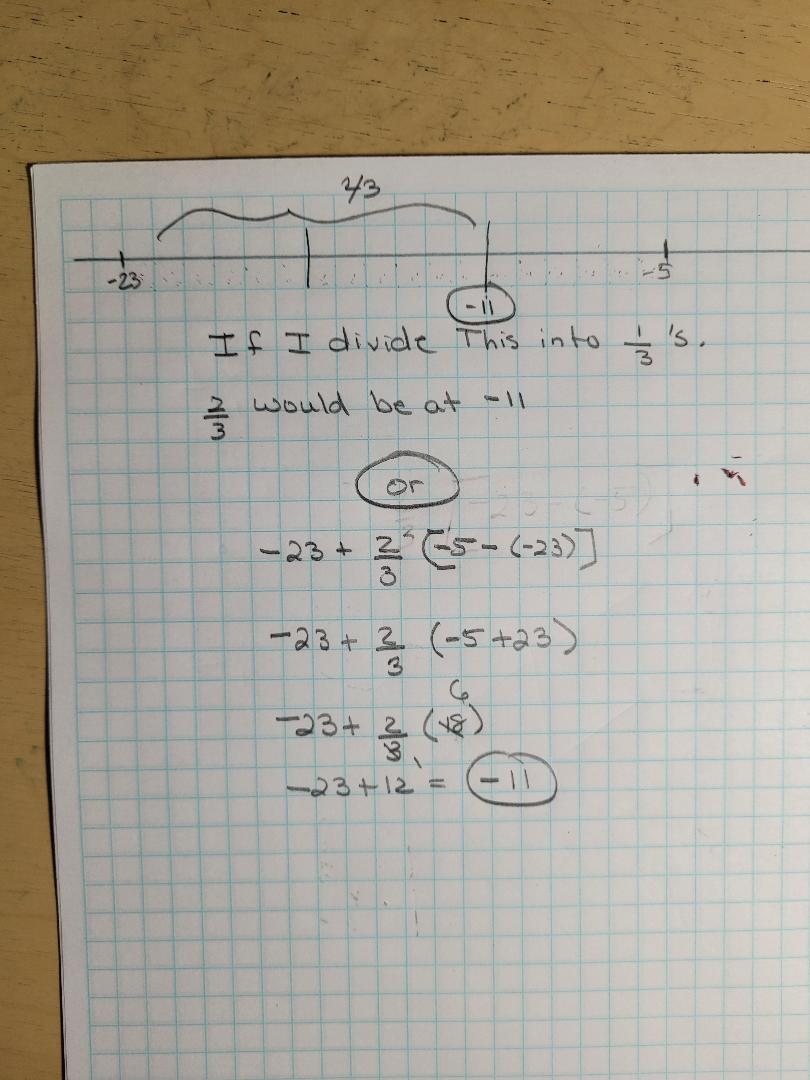
What is the distance from point A to point B? What is the perimeter of the shape?
Answers
2. The perimeter is the length of the outline of a shape. To find the perimeter of a rectangle or square you have to add the lengths of all the four sides.
Answer:
first one is 8 second one is 28
Step-by-step explanation:
correct on edge
Help me please and thank u love :) !?

Answers
Therefore , the solution of the given problem of unitary method comes out to be music video cost = $1.99.
What exactly is a unitary method?After establishing the size of a little slice, multiply the quantity by two to complete a task utilizing unitary technique. Simply expression the unit technique serves to isolate a programmed thing from a certain set or sets of sets. For example, the price of 40 pens is 400 pounds ($1.01) or Rs. It's possible that one country will have total control over the method employed to do this. Almost every living creature has a distinctive quality. It can equally integrate and reciprocate (mathematics, algebra).
Here,
Given :
2 music videos , a TV series and a movie worth $42.95
Let x be the cost of movie
From given information,
we can say
Cost of TV series = 2x
So ,
equation comes out to be x = 12.99 for movie
So TV series cost = 2 * 12.99 = 25.98
So ,
=> 2 music videos + 25.98 + 12.99 = 42.95
=> 2 music videos + 38.97 = 42.95
=> 2 music videos = 42.95 - 38.97
=> music video cost = 3.98 /2
=> music video cost = $1.99
Therefore , the solution of the given problem of unitary method comes out to be music video cost = $1.99.
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ1
Solve these Exponents

Answers
1. 1/4^5
2. 8^3
3. = 3^3 x 3^20
= 3^23
4. = 4^3 x 4^2 + 12^2
= 64 x 16 + 144
= 1024 + 144
= 1168
5. = 3^2 - 1
= 9 - 1
= 8
*Any number power by 0 will = 1*
Hope this helps :D
We have
components that we will put to use in a sequential fashion. That is, the component
is initially put in use, and upon failure, it is replaced by a component
, which is itself replaced upon failure by a componentlocalid="1649784865723"
, and so on. If the lifetime of component i is exponentially distributed with a mean
estimate the probability that the total life of all components will exceed
. Now repeat when the life distribution of component i is uniformly distributed over
.
- the lifetime of the component is exponentially distributed
.
- the lifetime of the component is uniformly distributed
.
Answers
1) The probability density function is 1 - ∫[0, 1200] f(x) dx.
2) The probability density function is 1 - ∫[0, 1200] f(x) dx.
To estimate the probability that the total life of all components will exceed 1200, we need to consider two scenarios: one with exponentially distributed lifetimes and another with uniformly distributed lifetimes.
1) Exponentially Distributed Lifetimes:
Given that the lifetime of component i is exponentially distributed with a mean of 10 + i/10, we can calculate the failure rate (λ) for each component as λ = 1 / mean.
The total life of all components can be modeled as a sum of exponentially distributed random variables. Since the sum of exponential random variables follows a gamma distribution, we can use the gamma distribution to estimate the probability.
Let's denote the lifetime of component i as Xi, and the total life of all components as T = X1 + X2 + ... + X100.
The mean of the gamma distribution for the total life is given by E(T) = Σ(E(Xi)) = Σ(1 / λi), where λi is the failure rate of component i.
1.1 Calculation:
The probability that the total life of all components will exceed 1200 can be estimated as follows:
P(T > 1200) = 1 - P(T ≤ 1200)
= 1 - ∫[0, 1200] f(x) dx,
where f(x) is the probability density function of the gamma distribution with appropriate parameters.
2) Uniformly Distributed Lifetimes:
Given that the lifetime of component i is uniformly distributed over (0, 20 + i/5), we can calculate the mean lifetime for each component using the formula for the mean of a continuous uniform distribution: mean = (a + b) / 2, where a and b are the endpoints of the distribution.
The total life of all components can be modeled as the sum of uniformly distributed random variables. Since the sum of uniform random variables follows a Irwin-Hall distribution, we can use the Irwin-Hall distribution to estimate the probability.
Again, let's denote the lifetime of component i as Xi, and the total life of all components as T = X1 + X2 + ... + X100.
The mean of the Irwin-Hall distribution for the total life is given by E(T) = Σ(E(Xi)) = Σ((a + b) / 2), where a and b are the endpoints of the uniform distribution for each component.
2.1 Calculation:
Similarly, we can estimate the probability that the total life of all components will exceed 1200 using the Irwin-Hall distribution:
P(T > 1200) = 1 - P(T ≤ 1200)
= 1 - ∫[0, 1200] f(x) dx,
where f(x) is the probability density function of the Irwin-Hall distribution with appropriate parameters.
Correct Question :
We have 100 components that we will put in use in a sequential fashion. That is, component 1 is initially put in use, and upon failure, it is replaced by component 2, which is itself replaced upon failure by component 3, and so on. If the lifetime of component i is exponentially distributed with mean 10 + i/ 10, i = 1, . . . , 100, estimate the probability that the total life of all components will exceed 1200. Now repeat when the life distribution of component i is uniformly distributed over ( 0, 20 + i/ 5), i = 1, . . . , 100.
To learn more about probability density function here:
https://brainly.com/question/31039386
#SPJ4
If x is a positive integer, then x is _____ negative.
a. never
b. sometimes
c. always
Answers
because you are limiting x from 0 to infinite, and all of these are positive.
The sum of (-12) and (5) is
(A) 6 (B) 8 (C) -7
Answers
Answer:
-7
Step-by-step explanation:
-12 +5
Since the signs are different
Take the larger number and subtract the smaller number
12-5 =7
Take the sign of the larger
-7
Answer:
-7 is the answer
\(( - 12) + (5) \\ = 7\)
I NEED HELP!
Please try
Determine point C and the location of point C on the number line if point sea is 1/6 of the distance from point B to point A.
A14 D50
PHOTO ABOVE
HELPPPPP
Pls tryyy

Answers
20
Step-by-step explanation:
the distance from A to D is 36 units. One sixth of 36 is six. Six plus 14 is 20
There are 72 squares in the model. 72 squares What is the result of 72 divided by 12? 6 8 9 12
Answers
Answer:
6
Step-by-step explanation:
72 divided by 12 equals 6
Answer: it is (a)
explanation: in took the test :)
the radius of a circle is 10.4 ft. find the circumference \textit{to the nearest tenth}to the nearest tenth.
Answers
The circumference with radius of 10.4 ft is 65.3 ft. The result is obtained by using the formula for circumference.
What is circumference?Circumference is also called the perimeter of a circle. It can be expressed as
P = 2πr
Where
Radius of the circle = m.π = 22/7 or 3.14 ft.The circumference with the radius = 10.4 ft.
We have
Radius of a circle, r = 10.4 ftFind the circumference! (to the nearest tenth)
The circumference will be
P = 2πr
P = 2(3.14)(10.4)
P = 65.3 ft
Hence, the perimeter of the circle to the nearest tenth is 65.3 feet.
Learn more about perimeter of a circle here:
brainly.com/question/30432694
#SPJ4
I need help! Fine output when the input is N. Picture listed!

Answers
Answer:
Output is n - 4
Step-by-step explanation:
It follows a pattern. Output = Input - 4
Find the antiderivative: f(t) = 3t⁴ - t³ + 6t²/t⁴
Answers
Triangle UVW has vertices at U(−2, 0), V(−3, 1), W(−3, 3). Determine the vertices of image U′V′W′ if the preimage is rotated 180° counterclockwise.
U′(0, −2), V′(−1, −3), W′(−3, −3)
U′(0, −2), V′(1, −3), W′(3, −3)
U′(2, 0), V′(3, −1), W′(3, −3)
U′(−1, 0), V′(−3, 0), W′(3, −3)
Answers
To determine the vertices of image U′V′W′ after a 180° counterclockwise rotation, we can apply the following transformation rules:
A 180° counterclockwise rotation of a point (x, y) about the origin produces the point (-x, -y).To perform a rotation of a polygon, we apply the transformation rule to each vertex of the polygon.Using these rules, we can find the vertices of image U′V′W′ as follows:
Vertex U(-2, 0) is transformed to U′(0, -2), since (-(-2), -(0)) = (2, 0) becomes (0, -2) after the rotation.Vertex V(-3, 1) is transformed to V′(1, -3), since (-(-3), -(1)) = (3, -1) becomes (1, -3) after the rotation.Vertex W(-3, 3) is transformed to W′(3, -3), since (-(-3), -(3)) = (3, 3) becomes (3, -3) after the rotation.Therefore, the vertices of image U′V′W′ after a 180° counterclockwise rotation are U′(0, -2), V′(1, -3), and W′(3, -3).
So, the answer is option (b) U′(0, −2), V′(1, −3), W′(3, −3).
34. The table below shows the number of new restaurants in a fast food chain that opened during the years
of 1988 through 1992. Using an exponential model, write an equation for the curve of best fit, then
estimate the number of new restaurants that opened in 2005.
1486
Year
1988
1989
1990
1991
1992
New
Restaurants
49
81
112
150
262
Equation:
Answer:
Answers
As a result, we can assume that the fast-food business added about 3,454 new outlets in 2005.
What are equations used for?
A mathematical equation, such as 6 x 4 = 12 x 2, states that two variables or values are equivalent. a meaningful noun. An equation is used when two or maybe more factors must be considered jointly in order to understand or explain the whole situation.
We can apply the following formula to find an exponentially model that matches the data:
y = abˣ
Where x is the length of time after 1988, y is the number of fresh restaurants that open each year, and a and b are undetermined constants.
We may use the information from the years 1988 and 1989 to get the constants a and b:
49 = ab⁰
81 = ab¹
As a result of the first equation, a = 49. When we put it in the second equation, we obtain this result:
81 = 49b¹
b = 81/49
The following is the exponentially model that best matches the data:
y = 49(81/49)ˣ
Since 2005 is 17 years after 1988, we need to determine the value of y when x = 17 in order to figure out the number of new eateries that debuted in 2005:
y = 49(81/49)¹⁷
y ≈ 3,454
To know more about Equation visit:
https://brainly.com/question/29538993
#SPJ9
Simplify The Following

Answers
Answer:
(x+3) (x+4)/2x
Step-by-step explanation:
In ATUV, Y is the centroid. If TY = 30, what is YW?
A.15
B.45
C.30
D.60

Answers
We know at centroid medians bisect each other in the ratio 2:1.
TY=30Let YW be x\(\\ \sf\longmapsto TY=2x\)
\(\\ \sf\longmapsto 2x=30\)
\(\\ \sf\longmapsto x=\dfrac{30}{2}\)
\(\\ \sf\longmapsto x=15\)
Answer:
A
Step-by-step explanation:
On the median TW the distance from the vertex to the centroid is twice the distance from the centroid to the midpoint , then
YW = \(\frac{1}{2}\) × TY = \(\frac{1}{2}\) × 30 = 15
reflect (0,3) across the x axis
Answers
Answer: (3,0)
Step-by-step explanation: Since (0,3) is on the y-axis, it is basically a mirror to the x-axis. So, you just flip those numbers around which causes you to get (3,0). Have a nice day!
AABC has vertices (-6,2), B (5,-1), and C (4,4). Classify AABC by its sides. Then determine whether it is a right triangle. (Hint: Draw the picture).
Answers
The Pythagorean theorem is not satisfied since dAB² + dBC² ≠ dAC². Therefore, AABC is not a right triangle.
AABC is a scalene triangle with no sides of equal lengths. A triangle is said to be scalene when it has all its sides with different lengths. The side lengths of the AABC triangle can be calculated using the distance formula, which is given by'd = √((x2 - x1)² + (y2 - y1)²)Where d is the distance between two points (x1, y1) and (x2, y2).
Using the distance formula, we can calculate the length of each side of the AABC triangle. For side AB: dAB = √[(5 - (-6))² + (-1 - 2)²]= √(11² + (-3)²)= √130For side AC:dAC = √[(4 - (-6))² + (4 - 2)²]= √(10² + 2²)= √104For side BC:dBC = √[(4 - 5)² + (4 - (-1))²]= √((-1)² + 5²)= √26Since all the three sides have different lengths, the triangle AABC is a scalene triangle.
As for the second part of the question, we will check if it is a right triangle by determining if it has a right angle. We know that a right triangle is one that has one angle measuring exactly 90 degrees, and in such a triangle, the side opposite to the 90-degree angle is called the hypotenuse.
To determine if AABC is a right triangle, we can calculate the length of all the sides. Then we can check if the Pythagorean theorem holds, that is, the sum of the squares of the two smaller sides equals the square of the hypotenuse.If the Pythagorean theorem holds, then the triangle is a right triangle. If it doesn't, then the triangle is not a right triangle.
Using the distance formula above, we can determine the length of the three sides of the AABC triangle. Then we will compare the sides to determine if they satisfy the Pythagorean theorem. We have:dAB² + dBC² = √130² + √26²= 13,000 + 676= 13,676dAC² = √104²= 10,816
The Pythagorean theorem is not satisfied since dAB² + dBC² ≠ dAC².
Therefore, AABC is not a right triangle.
For more questions on Pythagorean .
https://brainly.com/question/21332040
#SPJ8
A billiard ball maker must place orders for resin, a raw material for billiard balls. It uses resin at a rate of 80 kilograms each day, and incurs a cost of $0.5 per kilogram per day to hold inventory. The ordering cost is $200 per order. Lead time for delivery is 4 days. Assume 365 day in a year.
If the order quantity is 1,600 kilograms, what is the ratio of the average inventory level in this scenario over the optimal average inventory (which is associated with the optimal order quantity)? [Round your final number with three decimals, if needed]
0.158
0.331
3.310
6.324
None of the above
Answers
The ratio of the average inventory level in this scenario over the optimal average inventory is approximately 0.103.
To find the ratio of the average inventory level in this scenario over the optimal average inventory, we need to calculate the average inventory levels for both scenarios.
For the given scenario:
Order Quantity = 1,600 kilograms
Daily Usage Rate = 80 kilograms/day
Lead Time = 4 days
Total Demand (annual) = 80 kilograms/day * 365 days
= 29,200 kilograms
Ordering Cost = $200 per order
Holding Cost = $0.5 per kilogram per day
Using the Economic Order Quantity (EOQ) formula, the optimal order quantity can be calculated as follows:
EOQ = √((2 * Ordering Cost * Total Demand) / Holding Cost)
= √((2 * $200 * 29,200) / $0.5)
= √(116,800,000)
≈ 10,806 kilograms
Now, let's calculate the average inventory level for the given scenario:
Average Inventory = (Order Quantity / 2) + (Daily Usage Rate * Lead Time)
= (1,600 / 2) + (80 * 4)
= 800 + 320
= 1,120 kilograms
To find the ratio, we divide the average inventory level for the given scenario by the optimal average inventory:
Ratio = Average Inventory / Optimal Average Inventory
= 1,120 / 10,806
≈ 0.103
To know more about average inventory,
https://brainly.com/question/28256013
#SPJ11
what is the squared root of 64?
Answers
Answer:
8
Step-by-step explanation:
Answer:
the square root is 8
Step-by-step explanation:
What percent of 300 is 0.6
Answers
Answer: 0.20 %
Step-by-step explanation:
300x= 0.60
x = .60/300 = 0.002
0.002 x 100 = 0.20%
The percentage equivalent is 0.02 .
Given,
Percent of 300 is 0.6
Here,
Let the number in percentage form be x ,
Now write the equation in terms of x,
300 * x% = 0.60
3x = 0.06
x = 0.02 %
Thus the percentage equivalent is 0.02% .
Know more about percentage,
https://brainly.com/question/23418123
#SPJ6
-7 5/6 . 1 3/5=
Help please
Answers
Answer:
-12.5333333333
Step-by-step explanation:
her3e
The ratio of boys to girls in the lunch room was 4 to 3. If there were 84 students in the cafeteria, how many were girls?
Answers
Step-by-step explanation:
9868866858566586575765578
El sueldo bruto de un trabajador de la educación es de 900.000 pesos, si el descuento total que le harán corresponde al 20% de su sueldo ¿Cuánto será su sueldo líquido?
Answers
Answer:
Sueldo neto= $160.000
Step-by-step explanation:
Dada la siguiente información:
Sueldo bruto= $200.000
Descuento total= 20%
Para calcular el sueldo neto, debemos usar la siguiente formula:
Sueldo neto= sueldo bruto* (1 - porcentaje de descuento)
Sueldo neto= 200.000*( 1 - 0.2)
Sueldo neto= $160.000