PLEASE HELP THIS IS DUE IN LIKE 2 HRS.
Carole compared function 1, y = 4x + 5, to function 2, a linear function that goes through the points shown in the table.
x y
-----------
2 12
4 24
6 36
8 48
Which function has the greater rate of change, and what is its rate of change?
A. Function 1 has the greater rate of change, and its rate of change is 4.
B. Function 1 has the greater rate of change, and its rate of change is 6.
C. Function 2 has the greater rate of change, and its rate of change is 4.
D. Function 2 has the greater rate of change, and its rate of change is 6.
Answers
Answer:
its (D) Function 2 has the greater rate of change, and its rate of change is 6.
Related Questions
The Point class represents x,y coordinates in a Cartesian plane. Which line of code appears completes this operator which transforms a Point by dx and dy? (Members written inline for this problem.) class Point { int x_{0}, y_{0};public: Point(int x, int y): x_{x}, y_{y} {} int x() const { return x_; } int y() const { return y_; }};Point operator+(int dx, int dy) { return _________________________;}
Answers
The correct line of code that completes this operator which transforms a Point by dx and dy is shown below: Point operator+(int dx, int dy) { return Point(x_+dx,y_+dy);}Note that the function operator+ takes two arguments: an integer dx and an integer dy.
The function returns a point, which is created by adding dx to x and dy to y.The completed code is shown below:class Point { int x_{0}, y_{0};public: Point(int x, int y): x_{x}, y_{y} {} int x() const { return x_; } int y() const { return y_; }};Point operator+(int dx, int dy) { return Point(x_+dx,y_+dy);}Therefore, the correct answer is: `Point(x_+dx,y_+dy)`
Learn more about operator
https://brainly.com/question/29949119
#SPJ11
could someone please help me with this? would be very much appreciated

Answers
Answer:
A. 7
B. 6
C. 70 degrees
Answer:
A. x=7
B. x=6
C. x= 40
Step-by-step explanation:
Trust me, I've been doing this kind of problems for 17 years. I'm an algebra teacher.
A principal of $4200 is invested at 8.25% interest, compounded annually. How much will the investment be worth after 11 years
Answers
Therefore, the investment will be worth $9757.23 after 11 years when a principal of $4200 is invested at 8.25% interest, compounded annually.
To find the amount that the investment will be worth after 11 years when a principal of $4200 is invested at 8.25% interest, compounded annually, we can use the formula: `A = P(1+r/n)^(nt)`
Where:
A = final amount
P = principal amount
r = annual interest rate (as a decimal)
n = number of times the interest is compounded per year
t = number of years
Let's substitute the given values into the formula and solve:
Given,
P = $4200,
r = 8.25%
= 0.0825,
n = 1 (compounded annually), and
t = 11 years.
Now, `A = 4200(1+0.0825/1)^(1*11)` = $9757.23 (rounded to two decimal places)
To know more about compounded annually visit:
https://brainly.com/question/31297006
#SPJ11
The wheels on Karin's bike are 64 inches in circumference. How many times do the wheels rotate if Karin rides 300 yards?
Answers
Answer: 169 times
Step-by-step explanation:
Circumference : 64inches
Distance: 300 yards
We know that 1 yard is 36 inches.
300yd*36 = 10800inches
10800/64 = 168.75 but rounding up makes it 169 times.
A merry-go-round has a circular platform with a radius of 5 feet. What is the platform's diameter?
Answers
Answer:
2.5
Step-by-step explanation:
5 by 2: 2.5
1. What is the equation of the line in standard form? A302-10

Answers
Question: What is the equation of the line in standard form?
The standard form for a line is :
y = mx + b
where m is the slope and b is the intercept with y axis.
First, we are going to find the slope, choosing any two points on the line. For example (X1, Y1) = (-4,0) and (X2, Y2) = (0,3). Then, by definition the slope is:
\(m\text{ = }\frac{Y2\text{ - Y1}}{X2\text{ - X1}}\text{ = }\frac{3-0}{0-(-4)}\text{ = }\frac{3}{0+\text{ 4}}\text{ = }\frac{3}{4}\)so, our new line equation would be:
\(y\text{ = mx + b = }\frac{3}{4}x\text{ + b}\)that is:
\(y\text{ = }\frac{3}{4}x\text{ + b}\)Now, we are going to find the y-intercept. This is also accomplished by picking two points on the line and solving for b. For example (X2, Y2) = (0,3). So, for above equation we have:
\(3\text{ = }\frac{3}{4}(0)\text{ + b}\)then
\(3\text{ = 0 + b = b}\)Then, we have b = 3.
Now, replacing the values of the slope and the intercept previously found, we obtain the equation of the line :
\(y\text{ = mx + b = }\frac{3}{4}x\text{ + }3\)that is
\(y\text{ = }\frac{3}{4}x\text{ + }3\)
Dawn deposited money into a savings account that earned no interest. After depositing the money, shemade withdrawals of $25.50 from the account at regular time intervals. After 12 withdrawals, the balanceof her account was $872. Which of the following equations models the balance, y, in dollars, of Dawn'ssavings account after x withdrawals?Oy=1,178 – 25.50xOy=872 – 25.50x= 566 - 25.50xOy=306 – 25.50xOy= 25.50 – 872X
Answers
To obtain the equation that models the balance in Dawn's savings account, the following steps are necessary:
Step 1: Interprete the question in terms of the values provided, as follows:
\(undefined\)the product of 7 and the quotient of 40 divided by 5 is
Answers
The quotient of 40 and 5
40÷5=8
=> Product of that number with 7 and 8
So number to find is : 7x8=56
The product of 7 and the quotient of 40 divided by 5 is 56.
What is the quotient?The quotient is the result which is derived by the division of two numbers.
For example, the quotient of 30 divided by 3 is 10.
What is the product of two numbers?The product is the multiplication of two numbers which is written as a*b.
For example, the product of 8 and 9 is 72.
Here given we have to calculate the product of 7 and the quotient of 40 divided by 5.
The quotient of 40 divided by 5 is 40/5= 8
The product of 7 and The quotient of 40 divided by 5= 7*8= 56
Therefore the product of 7 and the quotient of 40 divided by 5 is 56.
Learn more about quotient
here: https://brainly.com/question/673545
#SPJ2
umm..HELP me i don't get it!!!!!

Answers
Answer:
I think its C
Step-by-step explanation:
Because if you add the bottom together you get \(\frac{1}{\frac{1}{2x+5} }\). When you divide the bottom part flips so it would be \(1*2x+5\) which ends up being C
I think this is right but I may be wrong
Answer:
B
Step-by-step explanation:
Simplify the sum on the denominator, that is
\(\frac{1}{x+2}\) + \(\frac{1}{x+3}\)
multiply numerator/ denominator of first fraction by x + 3
Multiply numerator/ denominator of second fraction by x+ 2
= \(\frac{x+3}{(x+2)(x+3)}\) + \(\frac{x+2}{(x+2)(x+3)}\)
= \(\frac{2x+5}{x^2+5x+6}\)
The original fraction is now
\(\frac{1}{\frac{2x+5}{x^2+5x+6} }\)
= 1 × \(\frac{x^2+5x+6}{2x+5}\)
= \(\frac{x^2+5x+6}{2x+5}\) → B
Solve for x:
6x + 9 = 4x + 25
Answers
Answer:
x = 8
Step-by-step explanation:
Solve for x:
6 x + 9 = 4 x + 25
Subtract 4 x from both sides:
(6 x - 4 x) + 9 = (4 x - 4 x) + 25
6 x - 4 x = 2 x:
2 x + 9 = (4 x - 4 x) + 25
4 x - 4 x = 0:
2 x + 9 = 25
Subtract 9 from both sides:
2 x + (9 - 9) = 25 - 9
9 - 9 = 0:
2 x = 25 - 9
25 - 9 = 16:
2 x = 16
Divide both sides of 2 x = 16 by 2:
(2 x)/2 = 16/2
2/2 = 1:
x = 16/2
The gcd of 16 and 2 is 2, so 16/2 = (2×8)/(2×1) = 2/2×8 = 8:
Answer: x = 8
Yooooooo somebody help me...

Answers
Answer:
B
Step-by-step explanation:
algebra 7.5 factor the polynomial
x^2+5x+4
Answers
Answer:
( x + 4 ) ( x + 1 )
Step-by-step explanation:
x² + 5x + 4
= x² + 1x + 4x + 4
= x ( x + 1 ) + 4 ( x + 1 )
= ( x + 4 ) ( x + 1 )
Hence, factorised.
Determine whether each pair of expressions is equivalent. Explain your reasoning.

Answers
The answer is:
\(\large\textbf{They aren't equivalent.}}\)
In-depth explanation:
To determine the answer to this problem, we will use one of the exponent properties:
\(\sf{x^{-m}=\dfrac{1}{x^m}}\)
And
\(\sf{\dfrac{1}{x^{-m}}=x^m}\)
Now we apply this to the problem.
What is 4⁻³ equal to? Well according to the property, it's equal to:
\(\sf{4^{-3}=\dfrac{1}{4^3}}\)
And this question asks us if 4⁻³ is the same as 1/4⁻3.
Well according to the calculations performed above, they're not equivalent.
4. Show that the matrix [XX-X'Z(ZZ)-¹Z'X). where both the x & matrix X and the x matrix Z. have full column rank and m2, is positive definite. Discuss the implications of this result in econometrics.
Answers
To show that the matrix A = [XX - X'Z(ZZ)^(-1)Z'X] is positive definite, we need to demonstrate two properties: (1) A is symmetric, and (2) all eigenvalues of A are positive.
Symmetry: To show that A is symmetric, we need to prove that A' = A, where A' represents the transpose of A. Taking the transpose of A: A' = [XX - X'Z(ZZ)^(-1)Z'X]'. Using the properties of matrix transpose, we have:
A' = (XX)' - [X'Z(ZZ)^(-1)Z'X]'. The transpose of a sum of matrices is equal to the sum of their transposes, and the transpose of a product of matrices is equal to the product of their transposes in reverse order. Applying these properties, we get: A' = X'X - (X'Z(ZZ)^(-1)Z'X)'. The transpose of a transpose is equal to the original matrix, so: A' = X'X - X'Z(ZZ)^(-1)Z'X. Comparing this with the original matrix A, we can see that A' = A, which confirms that A is symmetric. Positive eigenvalues: To show that all eigenvalues of A are positive, we need to demonstrate that for any non-zero vector v, v'Av > 0, where v' represents the transpose of v. Considering the expression v'Av: v'Av = v'[XX - X'Z(ZZ)^(-1)Z'X]v
Expanding the expression using matrix multiplication : v'Av = v'X'Xv - v'X'Z(ZZ)^(-1)Z'Xv. Since X and Z have full column rank, X'X and ZZ' are positive definite matrices. Additionally, (ZZ)^(-1) is also positive definite. Thus, we can conclude that the second term in the expression, v'X'Z(ZZ)^(-1)Z'Xv, is positive definite.Therefore, v'Av = v'X'Xv - v'X'Z(ZZ)^(-1)Z'Xv > 0 for any non-zero vector v. Implications in econometrics: In econometrics, positive definiteness of a matrix has important implications. In particular, the positive definiteness of the matrix [XX - X'Z(ZZ)^(-1)Z'X] guarantees that it is invertible and plays a crucial role in statistical inference.
When conducting econometric analysis, this positive definiteness implies that the estimator associated with X and Z is consistent, efficient, and unbiased. It ensures that the estimated coefficients and their standard errors are well-defined and meaningful in econometric models. Furthermore, positive definiteness of the matrix helps in verifying the assumptions of econometric models, such as the assumption of non-multicollinearity among the regressors. It also ensures that the estimators are stable and robust to perturbations in the data. Overall, the positive definiteness of the matrix [XX - X'Z(ZZ)^(-1)Z'X] provides theoretical and practical foundations for reliable and valid statistical inference in econometrics.
To learn more about eigenvalues click here: brainly.com/question/29861415
#SPJ11
Given the data set below, which is the best measure of center? 5, 1, 3, 2, 12, 10, 63, 2, 7
Answers
Answer:
5
Step-by-step explanation:
Answer:
5
hope it helped you out
For z=4+3i and w=5−2i, find zw. That is, determine (4+3i)(5−2i) and simplify as much as possible, writing the result in the form a+bi, where a and b are real numbers.
Answers
To calculate the product \(\( zw \),\) we multiply the real parts and imaginary parts separately and combine them to obtain the final result.
Using the distributive property, we have:
\(( zw = (4 + 3i)(5 - 2i) \)\)
Expanding this expression, we get:
\(( zw = 4 \cdot 5 + 4 \cdot (-2i) + 3i \cdot 5 + 3i \cdot (-2i) \)\)
Simplifying further, we have:
\(zw = 20 - 8i + 15i - 6i^2 \)\)
Since \(\( i^2 \)\) is equal to -1, we can replace \(\( i^2 \)\) with -1:
\(\( zw = 20 - 8i + 15i - 6(-1) \)\)
Continuing to simplify:
\(\( zw = 20 - 8i + 15i + 6 \)\)
Combining like terms, we get:
\(\( zw = 26 + 7i \)\)
Therefore, the product of \(\( z = 4 + 3i \) and \( w = 5 - 2i \)\) is \(\( 26 + 7i \)\).
Learn more about Distributive Property here
https://brainly.com/question/30321732
#SPJ11
Solve.
x^1/2/y^1/2
x^1/2 * y^-1/2
Would the equations not change (leave as is) since they are
different variables?
Answers
In the given expressions, \(x^{1/2}/y^{1/2}\) and \(x^{1/2} * y^{-1/2}\), the variables x and y are treated independently.
In the first expression, \(x^{1/2}/y^{1/2}\), the square root operation is applied to x and y separately, and then the division operation is performed. This means that the square root is taken of x and y individually, and then their quotient is computed.
In the second expression,\(x^{1/2} * y^{-1/2}\), the square root operation is applied to x, and the reciprocal of the square root is taken for y. Then, the multiplication operation is performed.
Since x and y are considered as separate variables in both expressions, the equations do not change. The expressions are evaluated based on the individual values of x and y, without any interaction or dependence between them.
To know more about expressions,
https://brainly.com/question/29099574
#SPJ11
Use double integrals to find the area inside the curve r=3+sin(θ).
Answers
We will integrate over the region bounded by the curve and the x-axis, and between the limits of θ=0 and θ=2π. The resulting integral is evaluated as a definite integral to find the area of the region, which turns out to be 6π.
To find the area inside the curve r=3+sin(θ), we first need to find the limits of integration. The curve r=3+sin(θ) intersects the x-axis when r=0, which happens at θ=π. Therefore, we can integrate over the region between θ=0 and θ=2π, bounded by the curve and the x-axis.
Next, we need to express the area element dA in terms of polar coordinates. The area element in polar coordinates is given by dA=r dr dθ. Therefore, the double integral for the area inside the curve is:
A = ∫∫R r dr dθ
where R is the region bounded by the curve and the x-axis, and between the limits of θ=0 and θ=2π.
Substituting r=3+sin(θ) and performing the integration with respect to r first, we get:
A = ∫0^2π ∫0^(3+sin(θ)) r dr dθ
= ∫0^2π [(3+sin(θ))^2 / 2] dθ
= (1/2) ∫0^2π (9+6sin(θ)+sin^2(θ)) dθ
= (1/2) [9(2π) + 0 + π]
= 6π
Therefore, the area inside the curve r=3+sin(θ) is 6π.
To learn more about integrals click here: brainly.com/question/31433890
#SPJ11
I Need help with my math homework

Answers
2.12.8
3.55
5.40
…..
i need help and i dont got much time 10 points

Answers
Answer:
The answer is 85°
Step-by-step explanation:
We know that the sum of all the angles of a triangle equals 180°. Therefore, since we know that <1=45° and <2=50°. If we add this together and then subtract them from 180° we get the missing angle. Visual:
50°+45°=95°
180°-95°=85°
If this helped please consider giving me a thanks, a good rating, and brainliest. It is always greatly appreciated! Thanks!
what is the sales tax of an item that is $40 with 4% rate of sales tax?
Answers
Answer:
$41.60
Step-by-step explanation:
:))
|a-i|= the square root of 37
Answers
Answer:
well the square root of 37 is 6.083
Step-by-step explanation:
for this problem I use 6 since 6×6=36 then that my ewser 6 because if I go one higher I am going to 37
Answer:
-6
Step-by-step explanation:
edge
How many solutions does this system have? x + 4 y = 6. y = 2 x minus 3a. one b. two c. an infinite number d. no solution
Answers
According to the graph, the system of equations x + 4y = 6 and y = 2 x -3 has one solution that is (2,1)
In math the term called graph is defined as a diagram showing the relation between variable quantities, typically of two variables, each measured along one of a pair of axes at right angles.
Here we know that the following equation are known:
=> x + 4y = 6
=> y = 2x - 3
And here we need to find the number of solution for the equations.
Here we have to plot the equation on the graph then we get the graph like the following.
While we looking into the graph, we have identified that the intersection point in the graph is (2,1) and there is no other intersecting point.
Therefore, option (a) is correct.
To know more about graph here.
https://brainly.com/question/17267403
#SPJ4

What is the percent of decrease from 100 to 42?
Answers
The percent of decrease from 100 to 42 is 58%
What is the percent decrease?As evident from the task content; the percentage decrease which connotes a decrease from 100 to 42 is to be determined.
Recall that the percentage decrease can be determined by the formula;
Percent decrease = Original value - New value / original value × 100
Original value = 100
New value = 42
So,
Percent decrease = Original value - New value / original value × 100
= (100 - 42) / 100 × 100
= 58 / 100 × 100
= 0.58 × 100
= 58%
Ultimately, the percentage decrease from 100 to 42 as required to be determined is; 58%.
Read more on percentage decrease:
https://brainly.com/question/24304697
#SPJ1
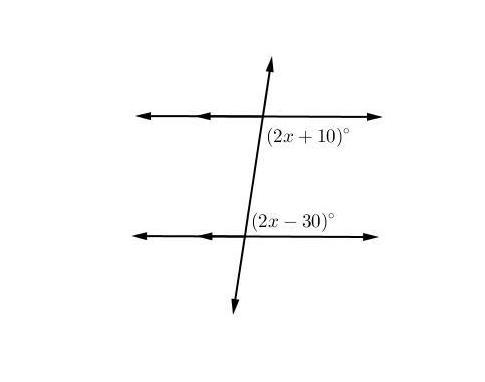
Examine the figure of two parallel lines cut by a transversal.
(2x + 10)°
What is the value of x?
(2x-30)
©2017 StrongMind. Created using GeoGebra
Answers
The value of x will be;
⇒ x = 50
What are Parallel lines?Parallel lines are those lines that are equidistance from each other and never intersect each other.
Given that;
Two parallel lines cut by a transversal.
Now,
Since, Two parallel lines cut by a transversal.
Hence, By definition of co-interior angle, we get;
The sum of co-interior angle in supplementary.
Hence, We get;
⇒ (2x + 10)° + (2x - 30)° = 180°
⇒ 4x - 20 = 180
⇒ 4x = 180 + 20
⇒ 4x = 200
⇒ x = 200/4
⇒ x = 50
Thus, The value of x = 50
Learn more about the parallel line visit:
https://brainly.com/question/26961508
#SPJ1
Linear Equations - Practice Word Problems
Solve.
#1 - When five is added to three more than a certain number, the result is 19. What is the number?
#2 - If five is subtracted from three times a ce3rtain number, the result is 10. What is the number?
Answers
Answer:
#1 - 11
#2 - 5
Step-by-step explanation:
#1 - This is really simple, as long as you don't think of it as numbers. The numbers 5 and 3 are being added to a number to make 19, so all you have to do is 19 - 5 - 3 or 19 - 8, which equals 11. So the certain number is 11.
#2 - The equation for this problem is (3 x ?) - 5 = 10. This equation is formed because you are subtracting 5 from 3 times a number, and to do all of this first, you need to figure out what 3 times a number equals (so it goes into the parentheses). From there, all you need to do is give a value that would substitute the question mark (normally you use a variable like n, x, y, etc.). This value would be 5, because 3 x 5 = 15 and 15 - 5 = 10.
:DDDDDDDDD
At a local department store sweaters typically cost $44. However due to a special the sweaters are reduced to $22. What percent of the original price has the sweater been reduced to
Answers
Answer:
50% reduction in price
Step-by-step explanation:
can be determined by 44- (44× X) solve for x and you get x as .5
State the equation of the graphed function.

Answers
The equation of the graphed function is given as follows:
f(x) = x³ + 2x² - 5x - 6.
How to obtain the equation of the function?
The equation of the function is obtained considering the Factor Theorem, as a product of the linear factors of the function.
From the graph, the zeros of the function are:
x = -3.x = -1.x = 2.Hence the function is:
f(x) = a(x + 3)(x + 1)(x - 2).
In which a is the leading coefficient.
Expanding the product, we have that:
f(x) = a(x² + 4x + 3)(x - 2)
f(x) = a(x³ + 2x² - 5x - 6).
When x = 0, y = -6, hence the leading coefficient a is obtained as follows:
-6a = -6
a = 1.
Hence the function is:
f(x) = x³ + 2x² - 5x - 6.
More can be learned about functions at https://brainly.com/question/24808124
#SPJ1
Given sin theta =
4/5 and pi/2 < theta < pi find cos 2theta
Answers
Answer: Since sin(theta) = 4/5 and pi/2 < theta < pi, theta is in the third quadrant.
In the third quadrant, cos(theta) is negative and sin(theta) is positive.
Using the double angle formula for cosine, cos 2theta = 2cos^2(theta) - 1 = 2(cos^2(theta) - (sin^2(theta)/2)) - 1
cos^2(theta) = 1 - sin^2(theta) = 1 - (4/5)^2 = 1 - 16/25 = 9/25
so,
cos 2theta = 2(9/25) - 1 = 18/25 - 25/25 = -7/25
Step-by-step explanation:
The value of the cos(2θ) will be equal to -24/25.
What is trigonometry?The relationships between the sides and angles of triangles are the subject of the mathematical discipline of trigonometry. It is based on research into the characteristics of the trigonometric functions used to describe these relationships, including sine, cosine, and tangent.
First, we can find the value of cos(θ) using the Pythagorean identity:
cos(θ = √(1 - sin^2(θ)) = √(1 - (4/5)²) = √(9/25) = 3/5
Since pi/2 < θ < π, we know that cos(θ) < 0. Therefore, cos(θ) = -3/5.
Next, we can use the double-angle formula for cosine to find cos(θ):
cos(θ) = 2cos²(θ) - 1
Substituting the value of cos(theta) that we found earlier, we get:
cos(2θ) = 2(-3/5)² - 1 = -24/25
Therefore, the value of the cos(2θ) = -24/25.
To know more about trigonometry follow
https://brainly.com/question/16174636
#SPJ2
What is the appropriate measure of variation (spread) for these data points? 47234213985132324365 what are q1 and q3 for these data?
Answers
The Interquartile Range (IQR) is the appropriate measure of variation for the given data points. Q1 and Q3 are 2 and 5 respectively.
The IQR is a method that gives the value of data at the 25th and 75th percentile. Alternatively, it gives the average of the two values which are nearest to these two percentiles, in case a single value does not exist. These values are called Q1 and Q3.
Because these values are less impacted by outliers than the standard deviation, it is best to use them with skewed data.
For the given data points, Q1 and Q3 are 2 and 5 respectively. Q1 is the average of 5th and 6th values. Q3 is the average of 15th and 16th values.
To learn more about the interquartile range, refer to this link:
brainly.com/question/11647487
The Interquartile Range (IQR) is the appropriate measure of variation for the given data points. Q1 and Q3 are 2 and 5 respectively.
The IQR is a method that gives the value of data at the 25th and 75th percentile. Alternatively, it gives the average of the two values which are nearest to these two percentiles, in case a single value does not exist. These values are called Q1 and Q3.
Because these values are less impacted by outliers than the standard deviation, it is best to use them with skewed data.
For the given data points, Q1 and Q3 are 2 and 5 respectively. Q1 is the average of 5th and 6th values. Q3 is the average of 15th and 16th values.
To learn more about the interquartile range, refer to this link:
brainly.com/question/11647487
#SPJ4