Please help this is 10 points only but please help my little sister needs help with this

Answers
Answer:
Step-by-step explanation:
the cost is $111
Related Questions
Need help with algebra 1b hw due at 8:39 am. Will pay anyone who helps with correct answers and shows work.

Answers
Answer:how much you paying
Step-by-step explanation:
Write an equation for the graph below in terms of x
Y=
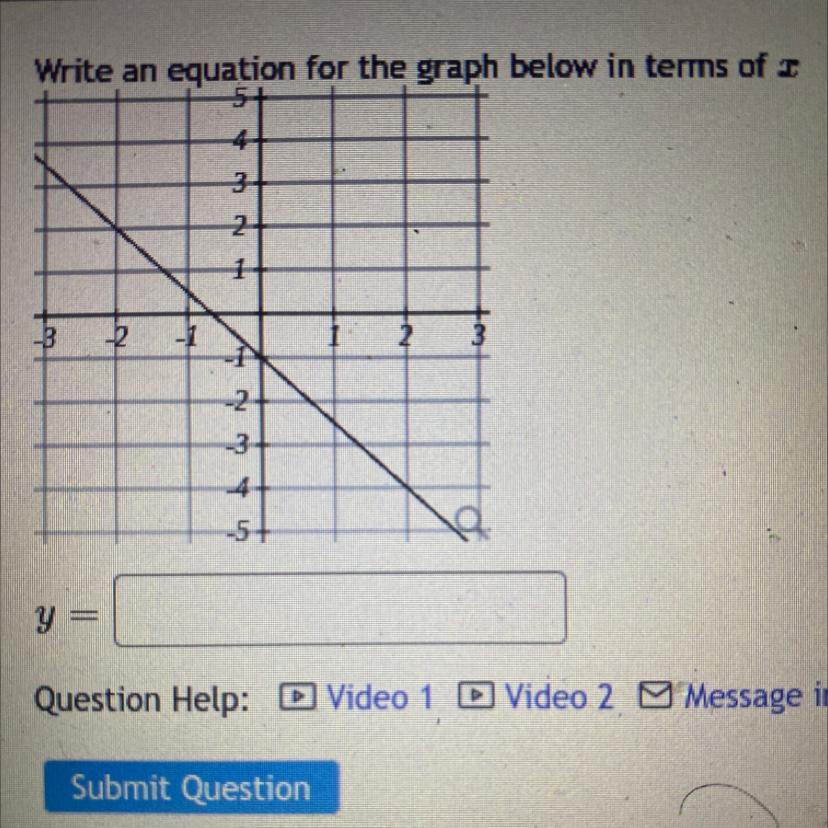
Answers
Because the slope is rise 3 run 2 and the y-intercept is -1
What point would represent a square with perimeter 20/21?
Answers
Answer:
P=4a
Step-by-step explanation:
calculate the perimeter of a square, add all the sides of it. There are 4 sides of a square which are all equal in length. The sum of the sides will give its perimeter. We can use also find the perimeter of square if the length of diagonal or area of square is given to us.
Need the help thanks guys

Answers
Answer:
Option D is the correct answer.
Step-by-step explanation:
The equation of the function is in vertex form. Thus, we can analyze the equation to determine the x and y values of the vertex. We know that the template format of a vertex form equation is as follows:
f(x) = a(x – h)2 + k . The only constants we need are h and k, where 'h' is the x-value of our vertex and 'k' is the y-value of our vertex.
The value of 'k' can be found quite simply by looking at the equation: -9.
The value of 'h' is a little trickier, as we must take into account the 'subtract' sign of the template equation, meaning that the '+7' in the given equation actually means that we are subtracting negative seven. Thus, the value of 'h' is -7.
Thus, the vertex of this graph is (-7,-9).
This means that option D is correct.
Answer:
The vertex is at ( -7, -9)
Step-by-step explanation:
y = (x+7)^2 -9
This is written in vertex form
y = a( x-h)^2 +k where ( h,k) is the vertex
y = ( x - -7)^2 + -9
The vertex is at ( -7, -9)
find x.
please and thank youuu

Answers
Answer:
x = 4√2
Step-by-step explanation:
Identifying the triangle in the diagram:
Whenever you see a right angle (its measure is 90°) and a 45°, the measure of the third angle is also 45° and the triangle is called a 45-45-90 triangle which has special rules, as it relates to the lengths of its sides.45-45-90 triangle rules:
The two sides across from the 45° are congruent and their lengths are x units long.The hypotenuse (always across from the right angle) is the longest side and its length is x√2 units long.Finding x:
Since the hypotenuse is 8 units long and, we can find x by setting 8 equal to x√2:
(8 = x√2) / √2
8/√2 = x
Rationalize the denominator to simplify:
When you have a fraction with a root as the denominator, we simplify (i.e. rationalize the denominator) by multiplying both the numerator and denominator by the root, which clears the root on the denominator:(8/√2) * (√2/√2)
8√2 / 2
4√2
Thus, x = 4√2
The slope of line BD is
y
2b
2a-c
E(a, b)
A(0, 0)
G
B(2a, 2b)
D(c, 0)
F
LL
C(2c, 0)
What is the equation of BD, simplified?
y - y₁ = m(x − x₁)
(x-c)
= √2²²= c)
2b
2a -
y -0 =
0 y = | D x - (₂22bcc)
b
C
1
2a -
0 y =
0 y = | 2²0 |x-12 2²0-c
2a
2a C
0 y = ( 2b )x - ( 2bc)
(2a-c) (2a - 2c)

Answers
Answer:
(c) y = 2b/(2a -c)x -2bc/(2a -c)
Step-by-step explanation:
Given the equation of line BD in point-slope form you want the simplified equation.
y -0 = (2b/(2a -c))(x -c)
SimplifiedThe equation is simplified by using the distributive property to eliminate parentheses.
\(y-0=\dfrac{2b}{2a-c}(x -c)\\\\\\y=\dfrac{2b}{2a-c}x-\dfrac{2b}{2a-c}c\\\\\\\boxed{y=\dfrac{2b}{2a-c}x-\dfrac{2bc}{2a-c}}\qquad\text{matches choice C}\)
<95141404393>
Three students have started a fence-painting business. Working together, Pragnesh and Qazi can paint the fence in 2 hours. Similarly, Pragnesh and Ronghui can paint the fence in 3 hours when they work together. Finally, when Qazi and Ronghui work together, they can paint the fence in 4 hours. How long would it take if all three students worked together to paint the fence
Answers
Answer: 55.4 mins
Step-by-step explanation:
pragnesh and qazi = 2hrs
pragnesh and roghui = 3hrs
qazi and roghui = 4hrs
this means for every 1 hour they wold paint.
pragnesh and qazi = \(\frac{1}{2}\) half of the fence
pragnesh and roghui = \(\frac{1}{3}\)
qazi and roghui = \(\frac{1}{4}\) quarter of the fence
time taken when they all work together
= \(\frac{1}{2}\) + \(\frac{1}{3}\) + \(\frac{1}{4}\)
= \(\frac{13}{12}\)
= \(\frac{12}{13}\)
= 0.9231 × 60(mins)
= 55.4 mins
solve for x
(look at photo)

Answers
By definition of proportion, the value of x is,
⇒ x = 80
We have to given that;
In a triangle,
Perpendicular = 60
Now, By Pythagoras theorem we get;
60² = 36² + y²
3600 = 1296 + y²
y² = 3600 - 1296
y² = 2304
y = 48
Hence, By definition of proportion;
⇒ x / 48 = 60 / 36
⇒ x = 80
Thus, By definition of proportion, the value of x is,
⇒ x = 80
Learn more about the proportion visit:
https://brainly.com/question/1496357
#SPJ1
In PQR, PQ= 5.4, QR= 3.6, and PR=6.2. To the nearest Tenth, what is M∠R
Answers
Therefore , the solution of the given problem of angles comes out to be M∠R measured at 45.4 degrees, to the closest tenth.
An angle meaning is what?The intersection of the lines that form a skew's ends determines the size of its biggest and smallest walls. There's a possibility that two paths will intersect at a junction. Angle is another outcome of two things interacting. They mirror dihedral forms the most. A two-dimensional curve can be created by placing two line beams in various configurations between their ends.
Here,
To determine the size of angle R in triangular PQR, we can apply the Law of Cosines:
=> cos(R) = (PQ₂ + PR₂ - QR₂) / (2 * PQ * PR)
=> cos(R) = (5.4₂ + 6.2₂ - 3.6₂) / (2 * 5.4 * 6.2)
=> cos(R) = 0.6960917
When we calculate the inverse cosine of both sides, we obtain:
=> R = cos⁻¹(0.6960917)
=> R equals 45.4 degrees
Angle R in triangle PQR is therefore measured at 45.4 degrees, to the closest tenth.
To know more about angles visit:
brainly.com/question/14569348
#SPJ1

how to solve this question

Answers
For the trigonometric identity
11. If cos 27° = x, then the value of tan 63° interims of "x" is x/√1 - x²
12. If Θ be an acute angle and 7sin²Θ + 3 cos²Θ= 4, then tan Θ is 1/√3
13. The value of tan 80° × tan 10° + sin² 70° + sin² 20° is 2
14. The value of (sin 47°/cos 43°)² + (cos 43°/sin 47°) - 4 cos²45° is 0
15. If 2 (cos²Θ - sin²Θ) = 1, Θ is a positive acute angle them the value of Θ is 30°
16. If 5 tan Θ = 4, then (5 sin Θ - 3 cos Θ)/(5 sin Θ + 2 cos Θ) is equal to 1/6
17. If sin(x + 20)° = cos (x + 10)° then the value of "x" is 30°
18. The value of (sin 65°)/ (cos 25°) is 1
How do we find the various trigonometric identity?To solve the various trigonometric identity;
11. Given: cos 27° = x
We know that cos (90 - θ) = sin θ
So, cos 63° = sin 27°
And sin 63° = √1 - cos²27°
Substituting cos 27° = x, we get
sin 63° = √1 - x²
Therefore, Therefore, tan 63° = sin 63° / cos 63° = cos 27° / cos 63° = x / cos 63°.
= x/√1 - x²
12. Given: Θ is an acute angle and 7sin²Θ + 3 cos²Θ= 4
Since Θ is an acute angle, sin²Θ + cos²Θ = 1
Substituting sin²Θ + cos²Θ = 1 into the equation 7sin²Θ + 3 cos²Θ= 4, we get
7 (sin²Θ/ cos²Θ) + 3 = 4/cos²Θ - 4 sec²Θ
⇒ 7tan²Θ + 3 = 4(1 + tan²Θ)
⇒ 7tan²Θ + 3 = 4 + 4 tan²Θ
⇒3 tan²Θ = 1
⇒ tan²Θ = 1/3
⇒ tanΘ = 1/√3
13. For tan 80° × tan 10° + sin² 70° + sin² 20°
⇒ tan 80° = cot (90 - 80)° = cot 10°
⇒ sin 70° = cos (90 - 70) = cos 20°
⇒ cot 10° × tan 10° + cos 20° + sin² 20°
= 1 + 1 = 2
14. (sin 47°/cos 43°)² + (cos 43°/sin 47°) - 4 cos²45°
= (sin 47°/cos43°)² + (cos 43°/sin 47°)² - 4(1/√2)²
= (sin (90° - 43°)/cos43°)² + (cos (90° - 47°)/sin)² = 4(1/2)
= (cos 43°/cos 43°)² + (sin 47°/ sin 47°)² - 2
= 1 + 1 - 2 = 0
15. 2 (cos²Θ - sin²Θ) = 1
cos²Θ - sin²Θ = 1/2
Since Θ is an acute angle, sin²Θ + cos²Θ = 1
Substituting sin²Θ + cos²Θ = 1 into the equation cos²Θ - sin²Θ = 1/2, we get
cos²Θ - (1 - cos²Θ) = 1/2
2cos²Θ = 3/2
cos Θ = √3/2(cos 30° = (√3)/2
= 30°
16. Given: 5 tan Θ = 4
We know that tan Θ = sin Θ / cos Θ
So, 5 sin Θ / cos Θ = 4
5 sin Θ = 4 cos Θ
Dividing both sides of the equation by 5, we get
sin Θ / cos Θ = 4/5
∴ sin Θ = 4/5 cos Θ
given that the expression is (5 sin Θ - 3 cos Θ)/(5 sin Θ + 2 cos Θ)
we substitute sin Θ = 4/5 cos Θ into the equation
⇒(5 × 4/5 cos Θ - 3 cos Θ)/(5 × 4/5 cos Θ + 2 cos Θ)
= (4-3)/(4 + 2) = 1/6
17. Given: sin(x + 20)° = cos (x + 10)°
We know that sin(90 - θ) = cos θ
So, sin(x - 20)° = sin(90 - (3x + 10))°
⇒ (x - 20)° = (90 - (3x + 10))°
⇒ x - 20° = 90° - 3x + 10
⇒ 4 x = 120°
⇒ x = 120°/4
⇒ x = 30°
18. To find the value of (sin 65°) / (cos 25°), we can use the trigonometric identity:
To solve this, we can use the following trigonometric identities:
sin(90 - θ) = cos θ
cos(90 - θ) = sin θ
We can also use the fact that sin²θ + cos²θ = 1.
Rewrite sin (65°) / cos (25°)
⇒ sin (65°) = cos (25°)
∴ cos (25°)/ cos (25°) = 1
Find more exercises on trigonometric identity;
https://brainly.com/question/24377281
#SPJ1
cual es la mediana de los datos en un estudio
Answers
Answer:
La mediana de un conjunto de números es el número del medio del conjunto (después de que los números se hayan ordenado de menor a mayor).
Step-by-step explanation:
Digamos que tienes estos números, 4, 7, 2, 9, 7, 6 y 4. primero, los pones en orden de menor a mayor (2, 4, 4, 6, 7, 7, 9), y luego usted determina qué número está en el medio, que es 6.
Solve the following and graph the solutions
3x +1 <10 and - 4x + 3 > - 17

Answers
9514 1404 393
Answer:
x < 3
Step-by-step explanation:
The solution to the first inequality is ...
3x +1 < 10
3x < 9 . . . . . . . subtract 1
x < 3 . . . . . . . . divide by 3
The solution to the second inequality is ...
-4x +3 > -17
-4x +20 > 0 . . . . . add 17
20 > 4x . . . . . . . . .add 4x
5 > x . . . . . . . . . . . divide by 4
Values of x that are both less than 5 and less than 3 must be less than 3. The solution is ...
x < 3

10. The total cost of shipping toys from a specific company is $5 plus $2.50 times the number of toys purchased
Answers
Answer:y=2.50x+5
Step-by-step explanation:
y=2.50x+5
that's all i can do with the information provided
Simplify the expression using the order of operations agreements.
-8÷2+2×8=
Answers
Answer:
12
Step-by-step explanation:
PEMDAS is the order
P = parenthesis
E = exponent
M = *
D = division
A = +
S = -
so first 8*2 = 16
and then -8/2 = -4
and then -4 + 16
= 12
1. Division; -8 divided by 2 = -4
2. Multiplication; 2 times 8 = 16
3. Add; -4 plus 16 = 12
Therefore the answer is 12.
I really need help with this

Answers
The prove that triangle ABE is congruent to triangle CDE is given below
What is congruence?Generally, To prove that triangle ABE is congruent to triangle CDE, we need to show that they have the same size and shape.
First, we can see that angle AED and angle CEB are opposite angles and therefore congruent, since AB || DC.
Also, since line AB = line DC, we know that segment AE is congruent to segment CE and segment BE is congruent to segment DE.
Using these congruent sides and the congruent angle, we can apply the Side-Angle-Side (SAS) congruence criterion to conclude that triangle ABE is congruent to triangle CDE.
Therefore, we have proven that triangle ABE is congruent to triangle CDE.
Read more about congruent angle
https://brainly.com/question/16448127
#SPJ1
x = 13, ¿cuál ecuación es verdadera?
3(18 - x) = 67
4(9x) = 23
2(x-3)=7
5(x-9) = 20
Answers
When x = 13, the equation that is true is option D) 5(x - 9) = 20.
To determine which equation is true when x = 13, we can substitute the value of x into each equation and see which equation holds true. Let's go through each option:
A) 3(18 - x) = 67
Substituting x = 13:
3(18 - 13) = 67
3(5) = 67
15 = 67
The equation is not true when x = 13. Therefore, option A is false.
B) 4(9x) = 23
Substituting x = 13:
4(9*13) = 23
4(117) = 23
468 = 23
Again, the equation is not true when x = 13. Therefore, option B is also false.
C) 2(x - 3) = 7
Substituting x = 13:
2(13 - 3) = 7
2(10) = 7
20 = 7
Once again, the equation is not true when x = 13. Therefore, option C is false as well.
D) 5(x - 9) = 20
Substituting x = 13:
5(13 - 9) = 20
5(4) = 20
20 = 20
Finally, the equation is true when x = 13. Therefore, option D is true.
For more such questions on equation visit:
https://brainly.com/question/30451972
#SPJ8
Note: the translated questions is
X = 13, which equation is true?
I NEED THE ANSWER ASAP
If you were to write the slope-intercept equation for a line that goes through the point (4,-3)--with a slope of -2--what would be the value of b?
y=mx+b
Answers
y=-2x+5 is the slope-intercept equation for a line that goes through the point (4,-3) and 5 is the value of b.
What is Slope of Line?The slope of the line is the ratio of the rise to the run, or rise divided by the run. It describes the steepness of line in the coordinate plane.
The slope intercept form of a line is y=mx+b, where m is slope and b is the y intercept.
The slope of line passing through two points (x₁, y₁) and (x₂, y₂) is
m=y₂-y₁/x₂-x₁
We have to find the slope-intercept equation for a line that goes through the point (4,-3)--with a slope of -2
m=-2
Now let us find the y intercept
-3=-2(4)+b
-3=-8+b
-3+8=b
5=b
Hence, y=-2x+5 is the slope-intercept equation for a line that goes through the point (4,-3) and 5 is the value of b.
To learn more on slope of line click:
https://brainly.com/question/14511992
#SPJ1
I need your knowledge.

Answers
Answer:
det(2*3) also det(6)
Step-by-step explanation:
this is just filler so I can send it
this is the Great common factor gcf

Answers
Answer:
6) 11
7) 1
8) 6
9) 1
10) 10
Step-by-step explanation:
I found the GCF for each of the following numbers.
Please Help! This is due in 3 hours!

Answers
Answer:
Jayden: 9t+3s=420
Carson: 1t+6s=296
Step-by-step explanation:
I hope that helps =)
10. Prime numbers from 1 to 100 are running a restaurant - PRIME SPOT, near a tourist point. On a winter holiday, 1 and the composite numbers up to 100 enter the restaurant for dinner after their picnic at the same point. The dining hall has tables with seating capacity 15 for each. If they occupy tables without leaving any chair free, how many tables are required? If each prime number attender has to serve equal number of customers, how many customers should each one get to serve?
Answers
6 tables are required. Each prime number attender should serve 3 customers each.
The prime numbers between 1 and 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
All the numbers other than prime numbers are composite numbers.
The composite numbers from 1 to 100 are: 1, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.
Now, as there are 25 primes and 75 composites in the group that visited the restaurant, we can calculate the number of tables required by dividing the number of people by the seating capacity of each table.
Each table has a seating capacity of 15, so the number of tables required will be: Number of tables = (Number of customers)/(Seating capacity of each table)Number of customers = 25 (the number of primes) + 75 (the number of composites) = 100Number of tables = 100/15 = 6 tables
Therefore, 6 tables are required.
Now, as each prime number attender has to serve an equal number of customers, we need to calculate how many customers each one should serve.
Each prime attender has to serve 75/25 = 3 customers each, as there are 75 composites and 25 primes.
Thus, each prime number attender should serve 3 customers each.
For more questions on prime number
https://brainly.com/question/145452
#SPJ8
What value for x makes the equation −10(x + 6) + 7x = 42 true?
Answers
Step-by-step explanation:
-10x-60+7x=42
-10x+7x=60+42
-3x=102
x=102/-3=34
tan theta equals 8 / 15 find sine theta + cos theta / cos theta (1 - cos theta)
Answers
I guess you have to find
\(\dfrac{\sin\theta+\cos\theta}{\cos\theta(1-\cos\theta)}\)
given that \(\tan\theta=\frac8{15}\).
We can immediately solve for \(\sec\theta\):
\(\sec^2\theta=1+\tan^2\theta\implies\sec\theta=\pm\dfrac{17}{15}\)
(without knowing anything else about \(\theta\), we cannot determine the sign)
Then we get \(\cos\theta\) for free:
\(\cos\theta=\dfrac1{\sec\theta}=\pm\dfrac{15}{17}\)
and we can now solve for \(\sin\theta\):
\(\sin^2\theta+\cos^2\theta=1\implies \sin\theta=\pm\dfrac8{17}\)
Notice that we have 2*2 = 4 possible choices of sign for either sin or cos.
• If both are positive, then
\(\dfrac{\sin\theta+\cos\theta}{\cos\theta(1-\cos\theta)}=\dfrac{391}{90}\)
• If both are negative, then
\(\dfrac{\sin\theta+\cos\theta}{\cos\theta(1-\cos\theta)}=\dfrac{391}{480}\)
• If sin is positive and cos is negative, then
\(\dfrac{\sin\theta+\cos\theta}{\cos\theta(1-\cos\theta)}=\dfrac{119}{480}\)
• If cos is positive and sin is negative, then
\(\dfrac{\sin\theta+\cos\theta}{\cos\theta(1-\cos\theta)}=\dfrac{119}{30}\)
Which expression is equivalent to 6^-2 x 6^4
Answers
Answer:
6^2 or 36
Step-by-step explanation:
Here we have two powers of the same base (6).
The pertinent rule is b^c * b^d = b^(c + and so here we have
6^(-2) * 6^4 = 6^(4 - 2) = 6^2 or 36
During July in Jacksonville florida
Answers
Answer:
yo i live in florida
Step-by-step explanation:
An account pays 7% per year simple interest. In year 1, the amount in the
account is
$950. How much is in the account in year 6?
Answers
The amount in year 6 is $1282.5.
What is simple interest?
Simple interest is a quick and easy method of calculating the interest charge on a loan. Simple interest is determined by multiplying the daily interest rate by the principal by the number of days that elapse between payments.
Given,
rate of interest = 7%
time = 1 year
Amount on first year = $950
First we will calculate simple interest for 5 years, because amount is available for 1 year.
SI =PRT
SI = 950(7/100)1
SI = $332.5
Therefore, the amount after 6 years = 950+332.5
=$1282.5
To know more about simple interest, visit:
https://brainly.com/question/3942189
#SPJ1
Michael walks 30 meters in 20 seconds. How many meters does he walk in per second?
Answers
Answer:
1.5 meters
Step-by-step explanation:
30/20 = 1.5
Answer:
1.5 meters per second.
Step-by-step explanation:
30/20=1.5
Hope I helped!
The picture below shows a shaded rectangular region inside a large rectangle.
What is the probability that a point chosen inside the large rectangle is not in the shaded region? (5 points)
A. 18%
B. 36%
C. 64%

Answers
Answer:
the answer is d
Step-by-step explanation:
true-false questions: justify your answers. 1.13 the solution set to a system of three equations in three unknowns cannot be a plane. 1.14 a system of linear equations cannot have only two solutions. 1.15 the solution set to a consistent rank 2 linear system in four unknowns would be a line in four-dimensional space. 1.16 a system of four equations in four unknowns always has a solution. 1.17 a system of four equations in four unknowns can have at most one solution. 1.18 the rank of a system is always less than or equal to the number of equations in the system. 1.19 use geometric reasoning to answer the following questions concerning systems (i) and (ii) below: (a) if (i) has exactly one solution, then the same is true for (ii). (b) if the solution set of (i) is a line, then the same is true for (ii). (c) if (i) has no solutions, then the same is true for (ii). (i) a1x b1y c1z
Answers
The True- False of given statements of Solutions of Equations are justified.
1.13 False. The solution set to a system of three equations in three unknowns can be a point, a line, or a plane. It depends on the system of equations and how they intersect in three-dimensional space.
1.14 False. A system of linear equations can have infinitely many solutions, one solution, or no solutions. It depends on the coefficients of the equations and the rank of the coefficient matrix.
1.15 False. The solution set to a consistent rank 2 linear system in four unknowns would be a plane in four-dimensional space, not a line.
1.16 False. A system of four equations in four unknowns may not have a solution, or it may have infinitely many solutions or one solution. It depends on the coefficients of the equations and the rank of the coefficient matrix.
1.17 False. A system of four equations in four unknowns can have infinitely many solutions or one solution, but it cannot have at most one solution.
1.18 True. The rank of a system is always less than or equal to the number of equations in the system.
1.19 (a) False. If (i) has exactly one solution, it does not necessarily mean that (ii) will have exactly one solution. It depends on the coefficients of the equations in (ii).
(b) False. If the solution set of (i) is a line, it does not necessarily mean that the same is true for (ii). It depends on the coefficients of the equations in (ii).
(c) True. If (i) has no solutions, then the same is true for (ii), since (ii) is equivalent to (i).
To know more about Solutions of Equations:
https://brainly.com/question/29757556
#SPJ4
The path of a baseball is modeled by the equation \(y= -0.25x^{2} +4x+3\\\) where x represents the time (in seconds) and y represents the height of the baseball.
- Find and interpret the y-intercept. Find the maximum height of the baseball. Then sketch a graph of the path.
(please provide steps on how to solve if you can)
Answers
The y-intercept is y = 3, and this is the initial height of the ball, and the maximum height is y = 19
What is the y-intercept?The y-intercept is what we get when we evaluate in x = 0, then:
y = -0.25*x² + 4x + 3
replacing x by zero we get:
y = -0.25*0² + 4*0 + 3 = 3
The y-intercept is y = 3.
The maximum height is at the vertex, we know this because the leading coefficient is negative, which means that the parabola opens down.
The vertex is at:
x = -4/(2*-0.25) = 8
Evaluating there:
y = -0.25*8² + 4*8 + 3 = 19
that is the maximum height.
Learn more about parabolas:
https://brainly.com/question/4061870
#SPJ1
![The path of a baseball is modeled by the equation [tex]y= -0.25x^{2} +4x+3\\[/tex] where x represents](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/WNYYlWe6mnbWY4OnAfccVBU1vKYSAOn2.png)