Answers
Answer:
Step-by-step explanation:
A: dividend;
B: divisor;
C: quotient
Related Questions
Graph this system of equations on the coordinate plane:
y=4/3x+4
3y=-2x-6
Answers
The graph the system of linear equations on a coordinate plane is added as an attachment
How to graph the system of linear equations on a coordinate plane?A system of linear equations is a collection of at least two linear equations.
In this case, the system of equations is given as
y=4/3x+4
3y=-2x-6
Rewrite the equations in the system of equations as follows:
So, we have the following representation
y = 4/3x + 4
3y = -2x - 6
Next, we plot the graph of the system of equations
In this case, the point of intersection of the equations represent the solution to the system
From the graph, the lines intersect at (-3, 0)
This means that the solution to the system of equations is (-3, 0)
See attachment for the graph of the system of equations
Read more about linear equations at
brainly.com/question/4074386
#SPJ1

if i have one
mom then she dies how many moms do i have
Answers
Answer:
Step-by-step explanation:
1-1=0
Answer:You will have 0 moms.
Step-by-step explanation:
First you take 1 away from 1.
After that you get your answer of 0.
In an elementary chemical reaction, single molecules of two reactants A and B form a molecule of the product C: A+B - C. The law of mass action states that the rate of reaction is proportional to the product of the concentrations of A and B: dc dt = k[A]B] (See Example 3.7.4.) Thus, if the initial concentrations are [A] = a moles/Land (B] = b moles/L and we write r = (C), then we have do dt ka - x)( - ) a. Assuming that a b, find as a function of t. Use the fact that the initial concentration of C is o. b. Find (t) assuming that a = b. How does this expression for a(t) simplify if it is known that 1 [C] - a after 20 seconds?
Answers
For the given elementary chemical reaction, the solution to the question is: C = a^2 * (1-t^2/400(1-a))
The question asks about calculating the concentration of C in a chemical reaction. Given that the reaction equation is as follows: A + B → C The rate of reaction can be expressed as: dc/dt = k[A][B] Where, k is the rate constant[A] is the concentration of reactant A in moles/L[B] is the concentration of reactant B in moles/L, c is the concentration of product C in moles/L
The initial concentration of A and B is [A] = a moles/L, [B] = b moles/L Let r be the rate of reaction, i.e. r = dc/dt Thus, using the equation r = k[A][B], we get r = k(a)(b)Now, we can write a differential equation for the concentration of C as follows: dc/dt = r, with initial concentration of C as 0 moles/L∴ dc/dt = kab
Substituting r = k(a)(b) in the equation, we get dc/dt = kabdc/db = kab*dt Differentiating both sides, we get, ln(C) = kab*t + C where C is a constant, ln(C) = ln(a^2) = 2ln(a) = C When a = b, the concentration of C will be maximum at t = (1/k)(ln(a)).
Thus the concentration of C as a function of time (when a = b) is given by C = a^2 * (1-t^2/2)If [C] = a after 20 seconds, then using the equation, we get a = a^2 * (1 - 20^2 * k^2/2)Therefore, 1 = a * (1 - 200k^2) Solving this equation for k, we get, k = ± sqrt[(1-a)/200a^2] For the positive value of k, the concentration of C as a function of time is given by C = a^2 * (1-t^2/400(1-a)).
To know more about elementary chemical reaction, refer here:
https://brainly.com/question/31022212#
#SPJ11
4. From the top of a tower 14m high, the angle of depression of a student is 32° Make a scale drawing and find the distance of the student from the foot of the tower to the nearest 1/2
Answers
The distance of the student from the foot of the tower is 25.63m the nearest 1/2 is 25.5m.
Given that From the top of a tower 14m high
The angle of depression of a student is 32°
we can use trigonometry to find the distance from the foot of the tower to the student:
tan(32°) = opposite/adjacent = 14/distance
Rearranging this equation gives:
distance = 14/tan(32°)
= 25.63m
Therefore, the distance of the student from the foot of the tower is approximately 25.63m nearest 1/2, this is 25.5m.
To learn more on trigonometry click:
https://brainly.com/question/25122835
#SPJ1
let f be the function defined by f(x)=x2 1x 1 with domain [0,[infinity]). the function f has no absolute maximum on its domain. why does this not contradict the extreme value theorem?
Answers
The function f(x) = x² - 1/x + 1, with domain [0, ∞), does not have an absolute maximum on its domain, but this does not contradict the extreme value theorem.
Determine the extreme value theorem?The extreme value theorem states that if a real-valued function f is continuous on a closed interval [a, b], then f must have both an absolute maximum and an absolute minimum on that interval.
However, the theorem does not apply to functions that have an open interval as their domain, such as f(x) = x² - 1/x + 1 with a domain of [0, ∞).
In this case, f(x) approaches infinity as x approaches 0, but it does not have a maximum value within the given domain. The lack of an absolute maximum for f(x) on [0, ∞) is consistent with the behavior of the function, and it does not violate the extreme value theorem since the domain is not a closed interval.
Therefore, the function f(x) = x² - 1/x + 1, defined on [0, ∞), lacks an absolute maximum, but this does not violate the extreme value theorem.
To know more about extreme value theorem, refer here:
https://brainly.com/question/30459993#
#SPJ4
What is the solution for the equation StartFraction 5 Over 3 b cubed minus 2 b squared minus 5 EndFraction
Answers
The solutions for the equation are b = 0, 3.
What is the cubic equation?
A three-degree equation is referred to as a cubic equation. All cubic equations have roots that are either three real roots or one real root and two imaginary roots. Polynomials are referred to as cubic polynomials if they have a degree of three. The opposite of cubing an integer is finding the cube root of that number. It can be determined by first determining how the given integer can be divided into prime factors, and then by using the cube root formula.
To find the solution for the equation 5/3b³ - 2b² - 5, we can factor it or use the quadratic formula.
One way to factor it is to note that it is a cubic equation in terms of b, and can be written as:
5/3b³ - 2b² - 5 = (5/3b³ - 2b²) - 5 = (5/3b³ - 2b²- 5b) + (5b)
= (5/3b)(b² - 3b) + 5
So, b=0 is one solution, but we can also factor the remaining quadratic equation (b² - 3b) = 0,
b=0 and b=3 are the solutions for the equation.
Hence, the solutions for the equation are b = 0, 3.
To learn more about the cubic equation visit,
https://brainly.com/question/30187457
#SPJ4
A company produces steel rods. The lengths of the steel rods are distributed with a mean of 154.4-cm and a standard deviation of 1.4-cm. For shipment, 10 steel rods are bundled together. What is the distribution of X
Answers
The variance of the mean length of the steel rods in a bundle of 10 is 0.196 cm².
The distribution of the mean lengths of the steel rods in a bundle of 10 can be approximated by a normal distribution.
The mean length of a single steel rod is given as 154.4 cm, and the standard deviation is 1.4 cm. When we bundle 10 rods together, the total length of the bundle is the sum of the lengths of the individual rods. Since the mean is a linear operator, the mean length of the bundle is simply the sum of the mean lengths of the individual rods, which is 10 times the mean of a single rod, or 10 * 154.4 = 1544 cm.
To calculate the variance of the mean length of the steel rods in the bundle, we need to consider the variance of the individual rods. Since the rods are bundled together, we assume that they are independent and identically distributed (i.i.d.).
The variance of the sum of independent random variables is equal to the sum of the variances of the individual random variables. Since we have 10 identical rods, the variance of the sum is 10 times the variance of a single rod. The variance of a single rod is the square of the standard deviation, which is (1.4 cm)² = 1.96 cm². Therefore, the variance of the sum of the lengths of the 10 rods is 10 * 1.96 = 19.6 cm².
To find the variance of the mean length of the steel rods in the bundle, we divide the variance of the sum by the number of rods in the bundle squared. In this case, it is 19.6 cm² divided by 10², which is 19.6 cm² divided by 100, resulting in 0.196 cm².
Therefore, the variance of the mean length of the steel rods in a bundle of 10 is 0.196 cm².
To know more about the variance, refer here:
https://brainly.com/question/31432390#
#SPJ11
considerastandard normal random variable z. what is the value ofzif the area to the right ofzis 0.2643?
Answers
To determine the value of the standard normal random variable z for which the area to the right of z is 0.2643, we can use the standard normal distribution table or a statistical software.
The value of z corresponding to an area to the right of z can be obtained by subtracting the given area from 1 since the area to the right is complementary to the area to the left. Therefore, the area to the left of z would be 1 - 0.2643 = 0.7357.
By referring to the standard normal distribution table or using a statistical software, we can find the z-value associated with an area of 0.7357. In this case, the z-value is approximately 0.611, indicating that the value of z for which the area to the right is 0.2643 is approximately 0.611.
To learn more about standard normal distribution click here : brainly.com/question/31327019
#SPJ11
The vertices of a triangle are A (2,5) B (1,2) and C (3,1) . Find the coordinates of the image after a dilation with respect to the origin using a scale factor of 2 and then a translation 2 units left and 1 unit up.

Answers
K=2
A'=2(2.5)=(4,10)B'=2(1,2)=(2,4)C'=2(3,1)=(6,2)Translation of 2 units left means change in x
A''=(4-2,10)=(2,10)B"=(2-2,4)=(0,4)C"=(6-2,2)=(4,2)Translation of 1 units up means change in y
A'''=(2,10+1)=(2,11)B'''=(0,4+1)=(0,5)C'''=(4,2+1)=(4,3)Answer:
See below ~
Step-by-step explanation:
Dilation of points with scale factor of 2 :
⇒ A = 2(2, 5) = (4, 10)
⇒ B = 2(1, 2) = (2, 4)
⇒ C = 2(3, 1) = (6, 2)
Translation 2 units left :
⇒ A' = (4 - 2, 10) = (2, 10)
⇒ B' = (2 - 2, 4) = (0, 4)
⇒ C' = (6 - 2, 2) = (4, 2)
Translation 1 unit up :
⇒ A" = (2, 10 + 1) = (2, 11)
⇒ B" = (0, 4 + 1) = (0, 5)
⇒ C" = (4, 2 + 1) = (4, 3)
1. Pusheen ran out of her front door, then slipped and fell. She got up and walked the rest of the way to the catnip patch down the block.
2. Terrence cycled rapidly down the hill that starts at his house. He then slowed down as he climbed up the other side towards the candy store.


Answers
I dont know if you want me to draw it but try drawing the first line for pusheen a little bit up but more to the right because she only went out the door. Next for her you want to make the line go straight to the right for a bit to say she tripped. Then have the line slowly rise because she is walking away from home not running anymore. Then stall it for the rest of the way.
Now lets start for terrence draw his line going up rapidly. Then start to lower the line bit by bit to show he slowed down going up the hill. For his it never stops so never make the line straight to the right for him.
This should be all hope this helps.
Answer:
The first image is for question 1, the second image is for question 2.
Step-by-step explanation:
Alright, let's say for #1 each little tic I drew on the x-axis and y-axis of the graph are intervals. Let's say for time, each tic is an interval of five seconds, and for distance from home, each tic is an interval of a few feet - maybe 3-5.
For #1, Pusheen runs a few feet from her house (running out of her front door signifies that) in around 10 seconds. Then, she falls. Let's assume it takes her another 10 or so seconds to get up. During that time, she doesn't move from the spot where she fell, but time continues, so x increases while y doesn't. Afterwards, she gets up and walks down the block. As she's walking, let's estimate that she goes about 10 feet within 20 seconds.
Boom. Question 1 is done.
Now, let's say for #2 each little tic I drew on the axes of the graph are intervals. Let's say for time, each tic is, once again, an interval of five seconds, and for distance from home, each tic is now an interval of 10 feet.
For #2, Terrence cycles down a hill from his house. (Basically, he rides a bicycle down from his house on the hill.) He's rapidly cycling, zooming down the hill pretty quickly. Let's say he moves a decent 30 feet in around 20 or so seconds. Not too bad. Afterwards, he slows down as he begins to climb the other side, presumably the other side of the hill, to reach the candy shop. Now, he's moving slower and climbing. Suddenly, he's only moving a few feet for every 5 seconds that passes.
Boom. Question 2 is done.


What does the slope tell you about the rate of change in elevation during Ryan's uphill climb? What was the total elevation change?

Answers
It should be noted that the slope shows that the rate of change in elevation rise at first but later reduced.
The total change in elevation is 10500 feet
How to explain the information?It should be noted that from the table, the time and the elevation has been given.
Therefore, the total elevation will be the addition of all the values given. This will be 10500 feet.
Also, the slope shows that the rate of change in elevation rise at first but later reduced.
Learn more about slope on:
brainly.com/question/16949303
#SPJ1
Need help on this question with some explanation "Graph the image of the figure on the right under the given translation". T(3,2) (x,y) . Thanks in advance!

Answers
ANSWER
\(A\)EXPLANATION
The given translation
\((3,2)\)This means the shape will be translated 3units to the right and 2 units up.
That is;
\(\begin{gathered} (x+3) \\ (y+2) \end{gathered}\)PLEASE HELP!!!! ASAP!!!! NO LINKS PLEASE

Answers
Answer:
yes it is proportional y is 1.2 times x
not proportional
Supposed 12 inches of wire cost $.72 at the same rate how much insensible 33 inches of wire cost
Answers
Answer:
$1.98
Step-by-step explanation:
12 ÷ 0.72 = 16.67
33 ÷ X = 16.67
X = 33 ÷ 16.67
=1.98
a class has eight girls and two boys. if the teacher randomly picks eight students, what is the probability that she will pick all girls? find the probability of the event.
Answers
Given that a class has 8 girls and 2 boys. The teacher randomly picks 8 students. We need to find the probability that she will pick all girls.
To find the probability of the event, we need to use the formula for the probability of an event, which is:
P (event) = Number of favorable outcomes / Total number of outcomes Probability of picking all girls out of 10 studentsSince there are 8 girls and 2 boys in the class, the total number of students is 10.
There are only 8 girls, so the only way to pick all girls is if all 8 girls are selected out of the 10 students.
Total number of outcomes = 10 C8 = 45 (number of ways to pick 8 students out of 10) Number of favorable outcomes = 1 (since there is only one way to pick all 8 girls)
Therefore, the probability of the teacher picking all girls is:P (all girls) = 1/45 Thus, the probability of the teacher randomly picking all girls out of 8 girls and 2 boys is 1/45.
For more questions on: probability
https://brainly.com/question/23417919
#SPJ8
in a manufacturing process, a random sample of 36 manufactured bolts has a mean length of 3 inches with a standard deviation of .3 inches. what is the 99 percent confidence interval for the true mean length of the manufactured bolt?
Answers
The 99% confidence interval for the true mean length of the manufactured bolt is (2.9177, 3.0823)
Here, we need to construct a 99% confidence interval for population mean (μ) is given by
μ = x + Zα/2 * σ/√n or μ = x - Zα/2 * σ/√n
where, μ = population mean
x = sample mean
= 3 inches
σ = population standard deviation
= 0.3 inches
Zα/2= z score for a two tailed test at level of significance α = 2.576( for a 99% confidence level)
So, the upper limit would be,
μ = 3 + 1.645 * (0.3/√36)
μ = 3 + 1.646 * (0.3/6)
μ = 3.0823
And the lower limit would be,
μ = 3 - 1.645 * (0.3/√36)
μ = 3 - 1.646 * (0.3/6)
μ = 2.9177
Hence, the 99% confidence interval is (2.9177, 3.0823)
Learn more about confidence interval here:
https://brainly.com/question/24131141
#SPJ4
An insect population after x months can be modeled by
the function g(x) = 11(1.2). Which statement is the
best interpretation of one of the values in this function?
A. The insect population increased by 12 insects each month
B. The insect population decreased by 12 insects each month
C. The insect population increased at a rate of 20% each month
D. The insect population decreased at a rate of 20% each
month
Answers
The given function is g(x) = 11(1.2), where x is the number of months that have passed since the start of the model.\
What is function?a function is a relation between two sets, known as the domain and the range, that assigns to each element of the domain a unique element of the range. The domain is the set of all possible inputs or arguments for the function, and the range is the set of all possible outputs or values that the function can produce.
The given function is g(x) = 11(1.2), where x is the number of months that have passed since the start of the model. The function does not have a variable that changes with time, which suggests that the insect population is not affected by any external factors such as predation or migration. Instead, the function has a constant value of 11(1.2) that represents the insect population at any time x.
The value 1.2 in the function represents the growth factor, which is a multiplier applied to the initial population of 11 insects. This growth factor indicates the rate at which the insect population increases over time. Specifically, the growth factor of 1.2 means that the insect population increases by 20% each month, since:
new population = initial population + (growth factor) * initial population
new population = 11 + (1.2) * 11
new population = 11 + 13.2
new population = 24.2
This means that after one month, the insect population would be 24.2, which is an increase of 13.2 insects or approximately 20%. Therefore, the best interpretation of the value 1.2 in the function is that it represents the rate of increase of the insect population, and the correct answer is C.
To know more about function , check out :
https://brainly.com/question/25638609
#SPJ1
is y=3x(x+5) linear or nonlinear?
Answers
Answer:
linearStep-by-step explanation:
John is 6 years older than frank. 6 years ago, John was twice as old as frank. How old are they both now?
Answers
Answer:
John is 18, Frank is 12.
Step-by-step explanation:
This is th eanswer because if John is older that Frank by 6 years, and ^ years ago, double his age, you have to find a number that is twice the number 6.
12 fits that description:
John Frank
12 6 Let's say these were the ages, twice as old as Frank, but the difference is still 6.
Now, John is 18 (six years later..) and Frank is 12.
I hope you understand the answer and it helps you. :)
Daily output of Marathon's Garyville, Lousiana, refinery is normally distributed with a mean of 232,000 barrels of crude oil per day with a standard deviation of 7,000 barrels.
What is the probability of producing less than 239,000 barrels? (Round your answer to 4 decimal places.)
Answers
The probability of producing less than 239,000 barrels is 0.8413.
The probability of producing less than 239,000 barrels can be found using the z-score formula. The z-score formula is given by:
z = (x - μ) / σ
Where x is the value we are interested in, μ is the mean, and σ is the standard deviation.
Plugging in the given values, we get:
z = (239,000 - 232,000) / 7,000
z = 1
Now, we can use the standard normal table to find the probability of producing less than 239,000 barrels. The standard normal table gives the probability of a value being less than a given z-score. For a z-score of 1, the probability is 0.8413.
You can learn more about probability at: brainly.com/question/30034780
#SPJ11
What is the value of y in the sequence below?
2,y,18, -54,162,
Answers
First, let's check if the sequence is geometric or arithmetric.
If arithmetric, the sequence will have common difference.
Arithmetric
\( \displaystyle \large{a_{n + 1} - a_n = d}\)
d stands for a common difference. Common Difference means that sequences must have same difference after subtracting.
Geometric
\( \displaystyle \large{ \frac{a_{n + 1}}{a_n} = r}\)
r stands for a common ratio.
To find the value of y, you can check the sequence. If we try subtracting the sequences, the differences are different. That means the sequences are not arithmetric. That only leaves the geometric sequence.
Let's check by dividing sequences.
We have:
2,y,18,-54,162,...Let's check by divide -54 by 18 and 162 by -54. We need to divide more than one so we can prove that the sequence is geometric.
\( \displaystyle \large{ \frac{ - 54}{18} = - 3 } \\ \displaystyle \large{ \frac{ 162}{ - 54} = - 3} \)
Hence, the sequence is geometric.
Because the common ratio is -3. Let these be the following:
\( \displaystyle \large{ a_{n + 1} = y } \\ \displaystyle \large{ a_n = 2 } \\ \displaystyle \large{ r = - 3 }\)
From the:
\( \displaystyle \large{ \frac{a_{n + 1}}{a_n} = r}\)
Substitute the values in.
\( \displaystyle \large{ \frac{y}{2} = - 3}\)
Multiply the whole equation by 2 to isolate y.
\( \displaystyle \large{ \frac{y}{2} \times 2 = - 3 \times 2} \\ \displaystyle \large{ y = - 6}\)
Therefore, the value of y is -6.
-7x+y=-19 In standard form
Answers
Answer: x= 1/7y + 19/7 (Standard form will be:7x−y=19)
Step-by-step explanation:
Step 1: Add -y to both sides.
−7x+y+−y=−19+−y
−7x=−y−19
Step 2: Divide both sides by -7.
−7x/−7
= −y−19/−7
x= 1/7y + 19/7
28% of the runners stopped to take a drink after the first lap if they're 175 Runners how many stop taking
Answers
Answer:
49 runners stopped for a drink of water after the first lap.
Step-by-step explanation:
175 x 0.28 = 49
Graph the equation. Y = 5/16( x - 1)( x - 9)
Answers
The word "equation" and related words in other languages can have slightly different meanings. For example, in French an equation is defined as containing one or more variables.
Equation:
In mathematics, an equation is a formula that indicates equality of two expressions by connecting them with an equal sign =. The solution of an equation involving a variable is to determine the value of the variable for which equality is true. The variable whose equation needs to be solved is called the unknown, and the value of the unknown that satisfies the equation is called the solution of the equation. There are two types of equations: identity and conditional. Equality is true for all values of a variable. Conditional equations are only true for certain values of a variable.
The given equation is Y = 5/16( x - 1)( x - 9)
Consider any random values of x = 1,2 and substitute the coordinate in the given equation to find the value of coordinate y.
y = 5/16 (x-1)(x-9)
⇒ 5/16 { x² - 9x- x + 9}
⇒ 5/16 { x² -10x +9}
⇒ 5x² - 50x + 45 ÷ 16
And
Putting x = 1,
5(1) -50(1) + 45 ÷ 16
= 0
Putting x = 0,
5(0) -50(0) + 45 ÷ 16
= 0
Thus, we have the required points as (0 ,0)
Learn more about Variable:
https://brainly.com/question/29583350
#SPJ4

generate ordered pairs for each function for x=-2,-1,0,1,2

Answers
x. y
-2. -5
-1. -2
0. 1
1. 4
2 7
need explanation?
19. Solve for x and y:
(y +20)
110°
70°
(2x + 40)°

Answers
Answer:
x=35°, y=50°
Step-by-step explanation:

HELP MWNOWWWWWWWW PLSSSSSSSSSSSSSSSSSSS

Answers
Answer:
134.4
Step-by-step explanation:
What is the answer to number 2?
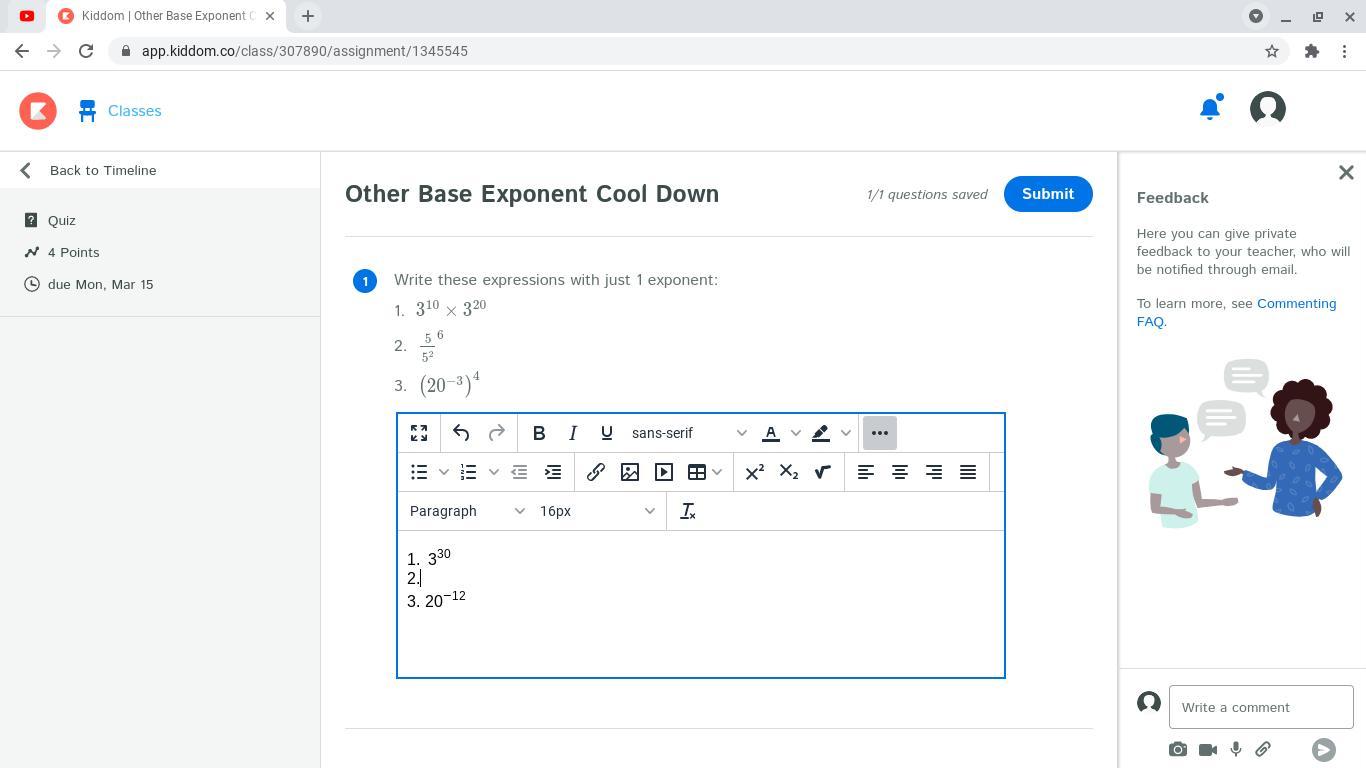
Answers
Answer:
5⁴
Step-by-step explanation:
→ Remember when dividing indices, minus them from each other
5⁶ ÷ 5² = 5 ⁶ ⁻ ² = 5⁴
using appropriate properties, find the value of 249² - 248²
Answers
Answer:
\(\boxed{\bold{\huge{\boxed{497}}}}\)
Step-by-step explanation:
=> \(\sf 249^2 - 248^2\)
Using Formula \(\sf a^2 - b^2 = (a+b)(a-b)\)
Where
a = 249
b = 248
=> \(\sf (249+248)(249-248)\)
=> \(\sf (497)(1)\)
=> 497
It is known that the lengths of songs played on a radio station follow a normal distribution with mean 3.9 minutes and standard deviation 0.4 minutes. A sample of 25 songs is randomly selected. What is the standard deviation of the sampling distribution of the sample mean length?
Answers
The standard deviation of the sampling distribution of the sample mean length for a sample of 25 songs is 0.04 minutes.
It is known that the lengths of songs played on a radio station follow a normal distribution with mean 3.9 minutes and standard deviation 0.4 minutes.
To find the standard deviation of the sampling distribution of the sample mean length for a sample of 25 songs, you can use the formula:
Standard deviation of sampling distribution = (population standard deviation) / √(sample size)
In this case, the population standard deviation is 0.4 minutes, and the sample size is 25. Plug these values into the formula:
Standard deviation of sampling distribution = 0.4 / √25 = 0.4 / 5 = 0.08 minutes
So, the standard deviation of the sampling distribution of the sample mean length for a sample of 25 songs is 0.08minutes.
Learn more about standard deviation here:
https://brainly.com/question/32016119
#SPJ12
