Please help me with this sorry if sideways if something is wrong let me know

The polynomial function is  \(f(x) = x^3+(\sqrt3-3)x^2+(2-3\sqrt3)x+2\sqrt3\).

The standard polynomial is given by:

f(x) = a(x-p)(x-q)(x-r) ...

Where a is the leading coefficient and p and q are the zeros.

Here We are given that the zeros are x = 1,2,and −√3.

Now leading Coefficient a = 1, p=1 , q=2 and r=−√3

Then the function is,

=> f(x) = 1(x-1)(x-2)(x-(−√3))

=> f(x)=(x-1)(x-2)(x+√3)

=> f(x)=\((x^2-2x-x+2)(x+\sqrt3)\)

=> \(f(x)=x^2-3x+2(x+\sqrt3)\)

=>\(f(x)=x^3+\sqrt3 x^2-3x^2-3\sqrt3 x+2x+2\sqrt3\)

=> \(f(x) = x^3+(\sqrt3-3)x^2+(2-3\sqrt3)x+2\sqrt3\)

Hence the polynomial function is \(f(x) = x^3+(\sqrt3-3)x^2+(2-3\sqrt3)x+2\sqrt3\).

To learn more about polynomial function refer the below link

https://brainly.com/question/2833285

#SPJ1

Answer:

Step-by-step explanation:

Area of the circular zone = \(\pi\)r^2

= 3.14 × 40^2 = 3.14 × 1600 = 5024 m^2

Area of the basketball court = l × b

= 30 × 15 = 450 m^2

Area of the trapezium shaped park =  ( 6 + 4 ) 3.5 / 2

= 35/2 = 17.5 m^2

∴ Area left in the circular zone = Area of the circular zone - ( Area of the basketball court + Area of the trapezium shaped park )

= 5024 - ( 450 + 17.5 )

= 5024 - 467.5

= 4556.5 m^2

hope this helps

plz mark it as brainliest!!!!!!!

Let's assume David's average speed is S km/h.

A) To find David's average speed, we can use the formula: Speed = Distance / Time.

David completed the race in 5 hours, so his speed is S km/h. Therefore, we have:

S = Distance / 5

B) Ken's average speed is 9.8 km/h less than David's average speed, which means Ken's average speed is (S - 9.8) km/h.

Ken took 7 hours to complete the race, so we have:

S - 9.8 = Distance / 7

Now, we can solve the system of equations to find the values of S and Distance.

From equation (1): S = Distance / 5

Substitute this into equation (2):

Distance / 5 - 9.8 = Distance / 7

Multiply both sides of the equation by 35 to eliminate the denominators:

7 * Distance - 35 * 9.8 = 5 * Distance

7 * Distance - 343 = 5 * Distance

Subtract 5 * Distance from both sides:

2 * Distance - 343 = 0

Add 343 to both sides:

2 * Distance = 343

Divide both sides by 2:

Distance = 343 / 2 = 171.5 km

Therefore, the distance of the cycling race is 171.5 kilometers.

To find David's average speed, substitute the distance into equation (1):

S = Distance / 5 = 171.5 / 5 = 34.3 km/h

So, David's average speed was 34.3 km/h.\(\)

Answer:

A) 34.3 km/h

B) 171.5 km

Step-by-step explanation:

Since Ken's average speed is said to be 9.8km/h less than David's average speed, and we know that Ken's average speed is dependent on him traveling for 7 hours, then we have our equation to get the distance of the cycling race:

\(\text{Ken's Avg. Speed}=\text{David's Avg. Speed}\,-\,9.8\\\\\frac{\text{Distance}}{7}=\frac{\text{Distance}}{5}-9.8\\\\\frac{5(\text{Distance})}{7}=\text{Distance}-49\\\\5(\text{Distance})=7(\text{Distance})-343\\\\-2(\text{Distance})=-343\\\\\text{Distance}=171.5\text{ km}\)

This distance for the cycling race can now be used to determine David's average speed:

\(\text{David's Avg. Speed}=\frac{\text{Distance}}{5}=\frac{171.5}{5}=34.3\text{ km/h}\)

Therefore, David's average speed was 34.3 km/h and the distance of the cycling race was 171.5 km.

By answering the presented question, we may conclude that In decimal form, the answer is 0.15, which is close to option A, 0.148. As a result, the answer is A. 0.148.

According to Euclidean geometry, a square is an equilateral quadrilateral having four equal sides and four equal angles. It is often referred to as a rectangle with two nearby sides of equal length. A square is an equilateral quadrilateral because it has four equal sides and four equal angles. Square angles are 90-degree or straight angles. Also, the diagonals of the square are evenly spaced and divide at a 90-degree angle. an adjacent rectangle with two equal sides. a quadrilateral with four equal-length sides and four right angles. A parallelogram with two adjacent, equal sides forming a right angle. A rhombus with straight sides.

To determine the answer, multiply the areas of the shaded squares by the overall area of the figure.

Assuming that both squares are the same size, we may combine the fractions using a common denominator:

2/12 + 2/15 = 5/60 + 4/60 = 9/60 = 3/20

As a result, the entire shaded area is 3/20 of the total area of the diagram.

We can't discover the exact area of the graphic because it's not presented. As a result, we can only represent the answer in fractions or decimals.

In decimal form, the answer is 0.15, which is close to option A, 0.148. As a result, the answer is A. 0.148.

To know more about square visit:

https://brainly.com/question/14198272

#SPJ1

The solutions are the values of x that makes the expression equal to zero:

x-5 =0

Add 5 to both sides

x=5

4x-5=0

Add five to both sides

4x=5

Divide both sides by 4

x= 5/4

x=1.25

Answer:

43/50

Step-by-step explanation:

86/100  Divide by 2

43/50

Can't be reduced anymore.

Hope this helped!

Answer: 800

Step-by-step explanation:

Answer:

4.80

Step-by-step explanation:

17+5.50h=11+6.75h

- subtract 11 from both sides

-subtract 5.50 from both sides

-divide to get h alone

Answer:

No idea on wht u are saying but, good luck

Answer:

2/5

Step-by-step explanation:

10 and 25 can both be divided by 5

10 divided by 5 equals 2

25 divided by 5 equals 5

Answer:a A. 4x-7/2x(x-2)

got it right on the test

Step-by-step explanation:

Answer:

Step-by-step explanation:

The given sequence can be written as:

a_1 = 8

a_2 = 10

a_3 = 12.5

a_4 = 15.625

To find the recursive formula, we need to find the common ratio (r) between consecutive terms:

r = a_2 / a_1 = 10 / 8 = 1.25

r = a_3 / a_2 = 12.5 / 10 = 1.25

r = a_4 / a_3 = 15.625 / 12.5 = 1.25

Since the common ratio is constant, we can use the formula for a geometric sequence to find the recursive formula:

a_n = r * a_{n-1}

Substituting r = 1.25 and a_1 = 8, we get:

a_n = 1.25 * a_{n-1}

Therefore, the recursive formula for the given sequence is:

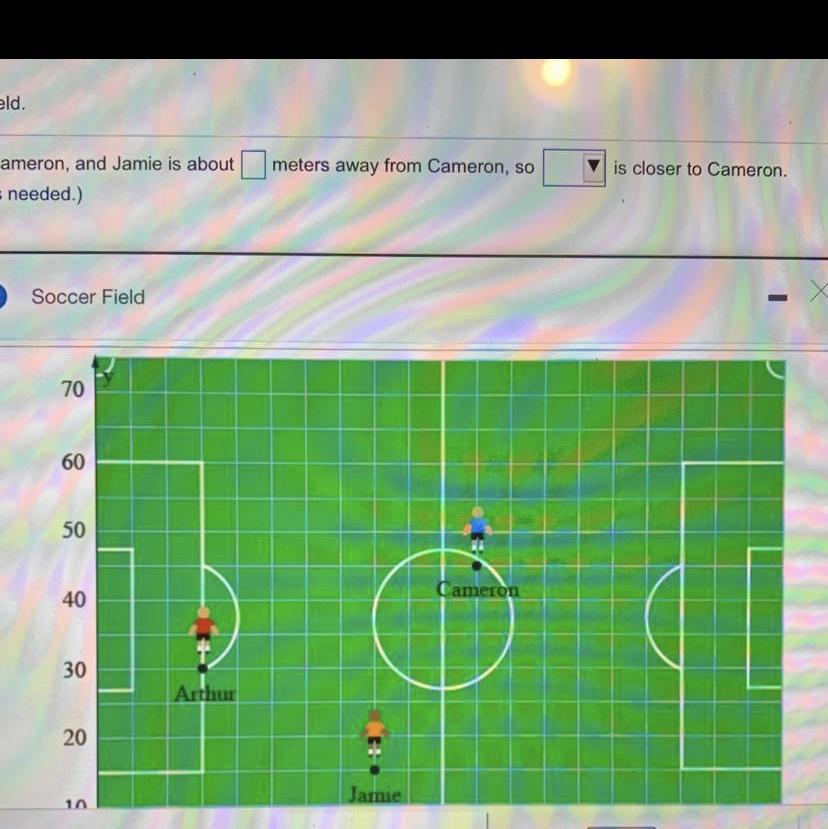
a_n = 1.25 * a_{n-1}, with a_1 = 8.

We need to use the distance formula:

d = √( (x2-x1)² + (y2-y1)² )

The coordinates of each player are:

Arthur : (15,30)

Jamie : (40, 15)

Cameron: (55,45)

Distance between arthur and jamie:

d = √( (40-15)² + (15-30)²) = 29.1548 = 29

Distance between arthur and cameron:

d = √( (55-15)² + (45-30)² ) = 42.72 = 43

Distance beetween jamie and cameron:

d = √( (55-40)² + (45-15)² ) = 33.54 = 34

Answer:

x = 21

Step-by-step explanation:

(x+6)^1/3 - 5= -2

add 5 to both sides of the equation:

(x+6)^1/3 = 3

cube both sides of the equation:

x + 6 = 27

subtract 6 from each side:

x = 21

Answer:

C. 72

Step-by-step explanation:

-3 x -2 = 6

6 x 3 = 18

18 x 4 = 72

Answer:

Step-by-step explanation:

this question involves negative and positive

so simple

Answer:

H0:  u = 185      against     Ha: u > 185

or

H0:  u ≤ 185      against     Ha: u > 185

Step-by-step explanation:

The null and alternative hypotheses for this experiment would be

H0:  u = 185      against     Ha: u > 185

or

H0:  u ≤ 185      against     Ha: u > 185

This is a one tailed test .

If the results are such that we reject the null hypothesis and accept the alternative hypothesis it means that the Americans are getting fatter as the mean weight is increasing day by day.

The null hypothesis deals with all the values equal to or less than 185 pounds and the alternative with all the values greater than 185  pounds.

Answer:

\(\displaystyle \lim_{x \to 2} \frac{x}{f(x)+1} = +\infty\)

Step-by-step explanation:

From the graph, we can see that:

\(\displaystyle \lim_{x \to 2} f(x)= -1\)

From direct substitution, we have that:

\(\displaystyle \lim_{x \to 2} \frac{x}{f(x)+1}\Rightarrow \frac{(2)}{-1+1}\)

Evaluate:

\(\displaystyle = \frac{2}{0}=\text{Und.}\)

Saying undefined (or unbounded) would be correct.

However, note that as x approaches two, the value of y decreases in order to get to negative one. In other words, our function f will always be greater or equal to negative one (you can also see this from the graph). This means that as x approaches two, f(x) will approach -0.99, -0.999 and -0.9999 and so on until it reaches negative one and then go back up. Importantly, because of this, we can state that:

\(\displaystyle \lim_{x \to 2} \frac{x}{f(x)+1}=\frac{(2)}{-1+1} = +\infty\)

This is because for the denominator, the +1 will always be greater than the f(x). This makes this increase towards positive infinity. Note that limits want the values of the function as it approaches it, not at it.

Answer:

undefined

Step-by-step explanation:

because

the figure does not appear

Answer:

Question:

If f and g are inverse functions, the domain of f is the same as the range of g.

Explanation:

If f: A → B is a bijective function, then the inverse function of f, say g will be a function such that g: B → A whose domain is B (which is a range of A) and range is A (which is the domain of f).

For example The trigonometric sine function,

is a bijective function with a domain

and range

Now the inverse sine function i.e.,

has the domain

equal to the range of the sine function and the range of the function as

equal to the domain of the sine function.

Therefore,

Therefore, the statement if f and g are inverse functions, the domain of f is the same as the range of g isTRUE

Answer:

$20

Step-by-step explanation:

To find out sale

50 x .25 = 12.5

To find out tax

37.5 x .06 = 2.25

Then final price

37.5 + 2.25 = 39.75

If they spilt price

$19.88

Answer:

1. $37.5 without tax

2. Split bill with tax: $19.88

3. Split bill withput tax: $18.25

Step-by-step explanation:

Make an equation first.

y=.25 (50)

This would help solve the amount for the discpunt sale.

The discout is $12.5 off.

50-12.5=37.5

Now we have tp solve for the tax amount.

y=0.06 (37.5)

y=2.25

2.25 is the tax amount.

We have to add these all together to get the answer for part 1.

37.5+2.25= $39.75

The function notation of 9x + 3y = 12 is given as follows:

f(x) = 4 - 3x.

The function in the context of this problem is given as follows:

9x + 3y = 12.

The format for the function notation is given as follows:

Hence we must isolate the variable y, as follows:

3y = 12 - 9x

y = 4 - 3x (each term of the expression is divided by 3).

f(x) = 4 - 3x.

More can be learned about functions at https://brainly.com/question/10687170

#SPJ1

Answer:

\(\displaystyle d = 2\sqrt{10}\)

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

Algebra I

Algebra II

Step-by-step explanation:

Step 1: Define

Point (-5, -2) → x₁ = -5, y₁ = -2

Point (-3, 4) → x₂ = -3, y₂ = 4

Step 2: Find distance d

Simply plug in the 2 coordinates into the distance formula to find distance d

The radius of curvature of the curve \(a^{2y\)=x³-a³ at the point where the curve intersects the x-axis is 27\(a^{\frac{3}{2}\).

To find the radius of curvature of the curve \(a^{2y\)=x³-a³ at the point where the curve intersects the x-axis, we need to first find the equation of the curve and then determine the value of y and its derivative at that point.

When the curve intersects the x-axis, y=0. Therefore, we have:

a⁰ = x³ - a³

x³ = a³

x = a

Next, we need to find the derivative of y with respect to x:

dy/dx = -2x/(3a²√(x³-a³))

At the point where x=a and y=0, we have:

dy/dx = -2a/(3a²√(a³-a³)) = 0

Therefore, the radius of curvature is given by:

R = (1/|d²y/dx²|) = (1/|d/dx(dy/dx)|)

To find d/dx(dy/dx), we need to differentiate the expression for dy/dx with respect to x:

d/dx(dy/dx) = -2/(3a²(x³-a³\()^{\frac{3}{2}\)) + 4x²/(9a⁴(x³-a³\()^{\frac{1}{2}\))

At x=a, we have:

d/dx(dy/dx) = -2/(3a²(a³-a³\()^{\frac{3}{2}\)) + 4a²/(9a⁴(a³-a³\()^{\frac{1}{2}\)) = -2/27a³

Therefore, the radius of curvature is:

R = (1/|-2/27a³|) = 27\(a^{\frac{3}{2}\)

To learn more about radius of curvature click on,

https://brainly.com/question/31403088

#SPJ1

Answer:

The maximum profit the florist will earn from selling celebration bouquets is $725.

The florist will break-even after one-dollar decreases when her profit is zero. From the graph, this occurs at x = 10. So the florist will break-even after 10 one-dollar decreases.

The interval of the number of one-dollar decreases for which the florist makes a profit from celebration bouquets is (0, 10). This is because the profit is positive for values of x between 0 and 10, and becomes negative after 10.

Step-by-step explanation:

A = 20

Use sine rule to find the other angles,

The domain and range of the given function is a set of al real numbers and as such;

Domain : (-∞,∞)

Range : (-∞,∞)

We are given the function as f(x)= -3x+7.

In order for us to sketch the graph of this given function, we need to make a function table

Lets assume some random number for x  and find out f(x)

x                f(x) = -3x + 7

-2                 -3(-2) + 7 = 13    

-1                 -3(-1) + 7 = 10

0                 -3(0) + 7 = 7

1                  -3(1) + 7 = 4

We now plot the points as shown in the graph attached

Domain is defined as the set of all x values for which the function is defined while Range is defined as the set of all y values for which the function is defined

In this case, there is no restriction for x  and y and as such the domain and range is a set of all real numbers

Domain : (-∞,∞)

Range : (-∞,∞)

Read more about Range and domain at; https://brainly.com/question/2264373

#SPJ1

Complete question is;

Given the following linear function sketch the graph of the function and find the domain and range. ƒ(x) = -3x + 7